Data Structure and Algorithms--Three Storage Structures of Trees
The linked list, queue and stack we learned before are all linear tables, because each data element has only one precursor and one successor. It's a one-to-one relationship.
What if it's a one-to-many relationship? This data structure is the tree to learn today.
Definition of tree
A tree is a set of finite nodes (assumed to be n). n = 0 means it's an empty tree. In a tree, there is and only one root node, which is customarily located at the top of the tree. The root knot can be understood as the existence of the ancestors. They have several children, but they have no parents themselves. In Figure 1, node A is the root node.
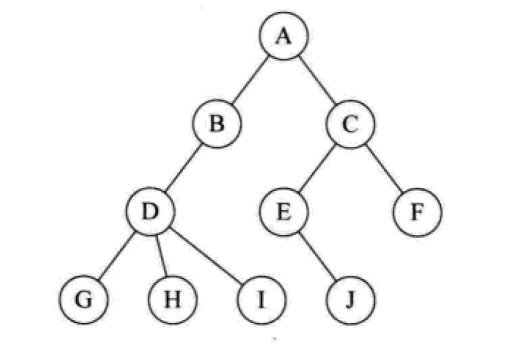
Assuming that the tree is truncated (not intersected), several disjoint (not intersected) sets can be obtained. Each set itself is a tree, called a root subtree, and then directly called a "subtree". For example, imagine that I disconnected A-B and A-C. Node B and C have no parents to become root nodes, resulting in two disjoint subtrees. As follows.
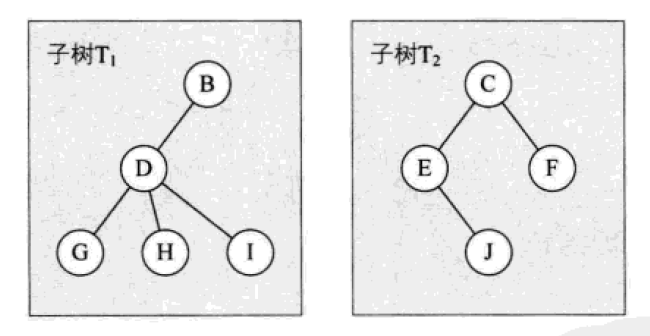
What is disjoint? Which tree do they belong to? It can be considered that there is intersection between the sets that constitute the subtree, which results in the intersection of the original subtree T1 and the subtree T2. Such intersecting trees are not called subtrees because they do not meet the definition of trees.
Nodes and Depth of Trees
Each circle in the figure above represents a node, and the lines between the nodes represent the relationship between the nodes. The number of subtrees owned by a node is called the degree of the node, which can also be simply understood as the number of children owned by the node. As in the figure above, the degree of node A is 2. A node with a degree of zero is called a leaf node -- that is, no child. Nodes whose degree is not zero are called non-leaf nodes or non-terminal nodes. The degree of the tree is the maximum of the degree of each node in the tree. In Figure 1, node D has three children, the most, so the degree of the tree is 3.
What is the relationship between the nodes in the tree? The root of a node's subtree is called the Child of the node, and the node is called the Parent of the Child, or the Parent node directly. Children of the same father node are called brothers. For example, in Figure 1, the Child nodes of node C are E and F, the father nodes of E and F are C, and the relationship between E and F is brotherhood.
The depth of a tree refers to the number of layers of the tree. The root node is the first layer, the child node is the second layer, and so on. It is easy to see that the depth of the tree in Figure 1 is 4.
Storage structure of tree
Parent Node Representation
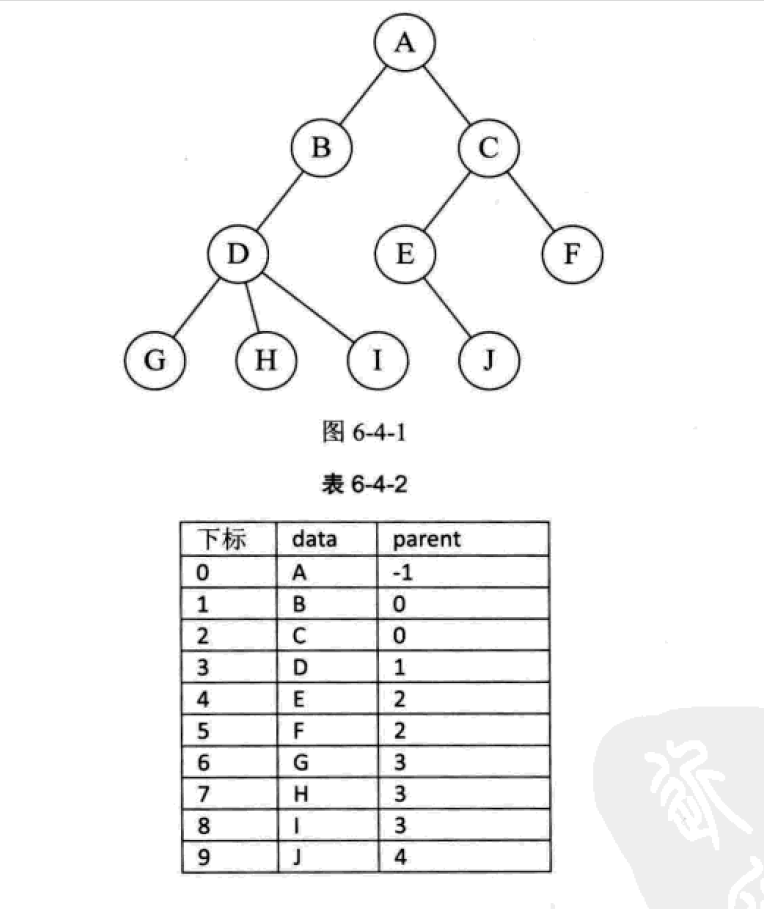
The idea of this structure is relatively simple: except that the root node has no father node, every other node has a unique father node. Store all nodes in an array. Each node has a data field and a numeric parent indicating the location of its parents in the array. Because the root node has no parent node, the parent is represented by - 1.
package Chap6; import java.util.ArrayList; import java.util.Arrays; import java.util.List; public class TreeParent<Item> { public static class Node<T> { private T data; private int parent; public Node(T data, int parent) { this.data = data; this.parent = parent; } public T getData() { return data; } @Override public String toString() { return "Node{" + "data=" + data + ", parent=" + parent + '}'; } } // The capacity of a tree, the maximum number of nodes it can hold private int treeCapacity; // Number of nodes in a tree private int nodesNum; // All nodes of the tree private Node<Item>[] nodes; // Initialize the tree with the specified root node and tree size public TreeParent(int treeCapacity) { this.treeCapacity = treeCapacity; nodes = new Node[treeCapacity]; } // Initialize the tree with the specified root node and default tree size public TreeParent() { treeCapacity = 128; nodes = new Node[treeCapacity]; } public void setRoot(Item data) { // Root node nodes[0] = new Node<>(data, -1); nodesNum++; } public void addChild(Item data, Node<Item> parent) { if (nodesNum < treeCapacity) { // The new node is placed in the first free position in the array nodes[nodesNum] = new Node<>(data, index(parent)); nodesNum++; } else { throw new RuntimeException("The tree is full, no more nodes can be added!"); } } // NoeNum is used because there is no null in it, and many null values in tree Capacity need not be compared at all. private int index(Node<Item> parent) { for (int i = 0; i < nodesNum; i++) { if (nodes[i].equals(parent)) { return i; } } throw new RuntimeException("No such node"); } public void createTree(List<Item> datas, List<Integer> parents) { if (datas.size() > treeCapacity) { throw new RuntimeException("Too much data, beyond the capacity of the tree!"); } setRoot(datas.get(0)); for (int i = 1; i < datas.size(); i++) { addChild(datas.get(i), nodes[parents.get(i - 1)]); } } // Is it an empty tree? public boolean isEmpty() { return nodesNum == 0; // or return nodes[0] == null } public Node<Item> parentTo(Node<Item> node) { return nodes[node.parent]; } // Node Children Node public List<Node<Item>> childrenFromNode(Node<Item> parent) { List<Node<Item>> children = new ArrayList<>(); for (int i = 0; i < nodesNum; i++) { if (nodes[i].parent == index(parent)) { children.add(nodes[i]); } } return children; } // Degree of tree public int degreeForTree() { int max = 0; for (int i = 0; i < nodesNum; i++) { if (childrenFromNode(nodes[i]).size() > max) { max = childrenFromNode(nodes[i]).size(); } } return max; } public int degreeForNode(Node<Item> node) { return childrenFromNode(node).size(); } // Depth of tree public int depth() { int max = 0; for (int i = 0; i < nodesNum; i++) { int currentDepth = 1; int parent = nodes[i].parent; while (parent != -1) { // Continue looking up for the parent node and know the root node parent = nodes[parent].parent; currentDepth++; } if (currentDepth > max) { max = currentDepth; } } return max; } // Number of nodes in a tree public int nodesNum() { return nodesNum; } // Return to the root node public Node<Item> root() { return nodes[0]; } // Let the tree be empty public void clear() { for (int i = 0; i < nodesNum; i++) { nodes[i] = null; nodesNum = 0; } } @Override public String toString() { StringBuilder sb = new StringBuilder(); sb.append("Tree{\n"); for (int i = 0; i < nodesNum - 1; i++) { sb.append(nodes[i]).append(", \n"); } sb.append(nodes[nodesNum - 1]).append("}"); return sb.toString(); } public static void main(String[] args) { // According to the following definition, spanning tree List<String> datas = new ArrayList<>(Arrays.asList("Bob", "Tom", "Jerry", "Rose", "Jack")); List<Integer> parents = new ArrayList<>(Arrays.asList(0, 0, 1, 2)); TreeParent<String> tree = new TreeParent<>(); tree.createTree(datas, parents); TreeParent.Node<String> root = tree.root(); // root's first child TreeParent.Node<String> aChild = tree.childrenFromNode(root).get(0); System.out.println(aChild.getData() + "The parent node is" + tree.parentTo(aChild).getData()); System.out.println("Root-knot children" + tree.childrenFromNode(root)); System.out.println("The depth of the tree is" + tree.depth()); System.out.println("The degree of the tree is" + tree.degreeForTree()); System.out.println("The number of nodes in the tree is" + tree.nodesNum()); System.out.println(tree); } } /* Outputs Tom The parent node is Bob The child of the root node [Node{data=Tom, parent=0}, Node{data=Jerry, parent=0}] The depth of the tree is 3. The tree has a degree of 2. The number of nodes in the tree is 5. Tree {Node{data=Bob, parent=-1}, Node{data=Tom, parent=0}, Node{data=Jerry, parent=0}, Node{data=Rose, parent=1}, Node{data=Jack, parent=2}} */
The setRoot method must be called first, and you can see that the root node is always placed in the first place in the array (subscript 0), before you can call the addChild method. CreateTree simplifies the process of creating a tree. We just need to input a set of data datas and pass the parents corresponding to this set of data to createTree. Note that the first data of data is the root node information. By default, -1 is used to represent its parent in the code, so it has no corresponding parent value in parents, that is to say, the second value of data corresponds to the first value of parents. And so on. After the tree is created, if you want to add nodes to the tree, call addChild.
The childrenFromNode method obtains all child nodes of a node, and the code shows that it needs to traverse all nodes with O(n) complexity. parentTo method obtains the parent node of a node with complexity O(1).
In addition, when calculating the degree of a tree, all nodes are traversed, and the maximum degree is chosen as the degree of the tree, and the complexity is O(n). The depth of the tree is similar, traversing all nodes from bottom to top, tracing back to the root node, recording the depth of the current node with current Depth, and selecting the maximum depth from all nodes as the depth of the tree.
Child Representation
In other words, since parental representation is a bit of a hassle for all children at a given node, we simply want each node to remember all of its children. But because the number of children a node has is an uncertain value, although at most only the degree of the tree is so much, but the number of children in most nodes is not so much, if we use an array to store all the children, it is too wasteful for most nodes. Naturally, it's easy to think of using a variable-capacity table to store, and using Java's built-in LinkedList is a good choice. First, an array is used to store all the node information. The linked list only needs to store the subscript of the node in the array.
package Chap6; import java.util.*; public class TreeChildren<Item> { public static class Node<T> { private T data; private List<Integer> children; public Node(T data) { this.data = data; children = new LinkedList<>(); } public Node(T data, List<Integer> children) { this.data = data; this.children = children; } public T getData() { return data; } @Override public String toString() { return "Node{" + "data=" + data + ", children=" + children + '}'; } } // The capacity of a tree, the maximum number of nodes it can hold private int treeCapacity; // Number of nodes in a tree private int nodesNum; // All nodes of the tree private Node<Item>[] nodes; public TreeChildren(int treeCapacity) { this.treeCapacity = treeCapacity; nodes = new Node[treeCapacity]; } public TreeChildren() { treeCapacity = 128; nodes = new Node[treeCapacity]; } public void setRoot(Item data) { nodes[0].data = data; nodesNum++; } public void addChild(Item data, Node<Item> parent) { if (nodesNum < treeCapacity) { // The new node is placed in the first free position in the array nodes[nodesNum] = new Node<>(data); // Parent node adds its children parent.children.add(nodesNum); nodesNum++; } else { throw new RuntimeException("The tree is full, no more nodes can be added!"); } } public void createTree(List<Item> datas, List<Integer>[] children) { if (datas.size() > treeCapacity) { throw new RuntimeException("Too much data, beyond the capacity of the tree!"); } for (int i = 0; i < datas.size(); i++) { nodes[i] = new Node<>(datas.get(i), children[i]); } nodesNum = datas.size(); } // Find the position in the rearrangement according to the given node private int index(Node<Item> node) { for (int i = 0; i < nodesNum; i++) { if (nodes[i].equals(node)) { return i; } } throw new RuntimeException("No such node"); } public List<Node<Item>> childrenFromNode(Node<Item> node) { List<Node<Item>> children = new ArrayList<>(); for (Integer i : node.children) { children.add(nodes[i]); } return children; } public Node<Item> parentTo(Node<Item> node) { for (int i = 0; i < nodesNum; i++) { if (nodes[i].children.contains(index(node))) { return nodes[i]; } } return null; } // Is it an empty tree? public boolean isEmpty() { return nodesNum == 0; // or return nodes[0] == null } // Depth of tree public int depth() { return nodeDepth(root()); } // Seek the depth of the subtree with node as the root node public int nodeDepth(Node<Item> node) { if (isEmpty()) { return 0; } // max is the maximum depth of all children in a node int max = 0; // Even without children, Return 1 is correct. if (node.children.size() > 0) { for (int i: node.children) { int depth = nodeDepth(nodes[i]); if (depth > max) { max = depth; } } } // This requires + 1 because depth - > Max is the child's depth of the current node, and + 1 is the depth of the current node. return max+1; } public int degree() { int max = 0; for (int i = 0; i < nodesNum; i++) { if (nodes[i].children.size() > max) { max = nodes[i].children.size(); } } return max; } public int degreeForNode(Node<Item> node) { return childrenFromNode(node).size(); } public Node<Item> root() { return nodes[0]; } // Number of nodes in a tree public int nodesNum() { return nodesNum; } // Let the tree be empty public void clear() { for (int i = 0; i < nodesNum; i++) { nodes[i] = null; nodesNum = 0; } } @Override public String toString() { StringBuilder sb = new StringBuilder(); sb.append("Tree{\n"); for (int i = 0; i < nodesNum - 1; i++) { sb.append(nodes[i]).append(", \n"); } sb.append(nodes[nodesNum - 1]).append("}"); return sb.toString(); } public static void main(String[] args) { List<String> datas = new ArrayList<>(Arrays.asList("Bob", "Tom", "Jerry", "Rose", "Jack")); List<Integer>[] children = new LinkedList[datas.size()]; children[0] = new LinkedList<>(Arrays.asList(1, 2)); children[1] = new LinkedList<>(Collections.singletonList(3)); children[2] = new LinkedList<>(Collections.singletonList(4)); children[3] = new LinkedList<>(); children[4] = new LinkedList<>(); TreeChildren<String> tree = new TreeChildren<>(); tree.createTree(datas, children); TreeChildren.Node<String> root = tree.root(); TreeChildren.Node<String> rightChild = tree.childrenFromNode(root).get(1); System.out.println(rightChild.getData()+"Degree is" + tree.degreeForNode(rightChild)); System.out.println("The number of nodes in the tree is"+tree.nodesNum()); System.out.println("The root node of the tree"+tree.root()); System.out.println("The depth of the tree is"+tree.depth()); System.out.println("The degree of the tree is"+tree.degree()); System.out.println(tree.parentTo(rightChild)); tree.addChild("Joe", root); System.out.println("The degree of the tree is"+tree.degree()); System.out.println(tree); } } /* Outputs Jerry The degree is 1. The number of nodes in the tree is 5. The root node Node{data=Bob, children=[1, 2]} The depth of the tree is 3. The tree has a degree of 2. Node{data=Bob, children=[1, 2]} The tree has a degree of 3. Tree{ Node{data=Bob, children=[1, 2, 5]}, Node{data=Tom, children=[3]}, Node{data=Jerry, children=[4]}, Node{data=Rose, children=[]}, Node{data=Jack, children=[]}, Node{data=Joe, children=[]}} */
Some methods are implemented as parental representations, while others are implemented differently.
The addChild parameter list remains unchanged, and the implementation becomes the subscript of the newly added node in the array (actually the first free position of the array) and adds into the child list of the parent node. createTree can be defined as a one-time spanning tree. It only needs to pass in the table of node information and the corresponding child list. The complexity is O(n). childrenFromNode gets all the children of a node, which is better than the parental representation. It does not traverse all nodes without judging if, but simply converts the contents of the child list (integer values) of the node into Node object returns. However, there is no parental method to obtain the parent node of a node in this implementation. The child representation must traverse all nodes with O(n) complexity. In the method of obtaining parent nodes, all nodes are traversed, and if a child list of a node contains the desired node, the node is returned.
The method of finding the depth of the tree has also become a recursive implementation. Because of the parent domain, it is more convenient to find from bottom to top in the implementation of parent method. In the child representation, it is more convenient to get the child nodes, so the idea of recursion is used here. Since max + 1 is returned (why this value will be explained later), the situation of tree empty needs to be correctly handled. If the leaf node does not execute the loop, it should return max + 1 = 1, which is correct; otherwise, the node has children and enters the loop and begins to recurse until the leaf node stops, starts to return, and the leaf node returns to 1. Back to the nodeDepth function of the parent node, Max is assigned a value of 1. Now let's talk about what this Max really means. In the code for (int i: node.children), all children traverse the current node, they share the same max, so the meaning of Max is the maximum depth of all children's nodes in a node. So max + 1 is the depth of the current node. Next, the function returns all the time. Each time it returns, it actually goes to the next level. At the child node of the desired node, the maximum depth of the child node is assigned to max. Then the max + 1 returned is the subtree depth when the node is the root node.
The optimization of children's expression method
In addition, the method of obtaining the parent node of a node can be seen from the code that it traverses all nodes. If you want to improve, you can merge the parental representation and add a parent field. That is to say, the Node class can be changed to the following, which can be called parental-child representation.
public static class Node<T> { private int parent; private T data; private List<Integer> children; }
In this way, the complexity of getting the parent node becomes O(1), and it's too lazy to implement it. Just change the code a little.
Child Brotherhood Representation
There is also a representation that focuses on the relationship between the children's nodes of a node, and they are brothers to each other. A node may have children, brothers, both, or neither. Based on this idea, a linked list with two pointer domains (one pointing to the child of the current node and one pointing to his brother) can be implemented, which is also called a binary linked list. Particular attention is paid to the fact that both parent and child node representations use arrays to store the information of each node. With a little analysis, it is necessary to use arrays. But in this structure, we abandon arrays, and the root node can be used as a header pointer, so that we can start to traverse all the nodes of the tree - the root node must have no brothers (if there are brothers, the tree has two root nodes), if it has no children, then the tree has only the root node; if there are children, the nextChild's pointer field will not be as follows. Now look at the left child, there are brothers (actually the second child of the root node) and children, then the two pointer fields of the left child are not empty. Look at the nextSib of the left child, he has a child... That's the way it goes, right, to access all the nodes of the tree.
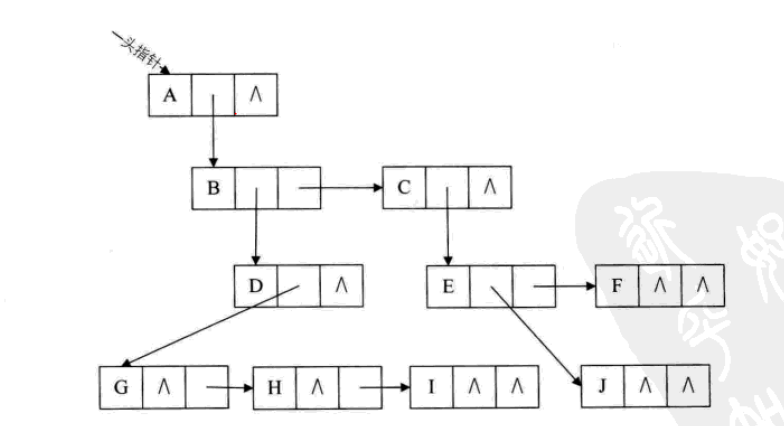
The whole structure is an intricate list with two directions, the vertical direction is the descendants that go deep into the node; the horizontal direction is to find its brothers and sisters. This structure can also visually reflect the structure of the tree, which is actually the tree below.

That's all. Anyway, just treat it as a linked list. It's just one more pointer field. (Unlike bi-directional lists, bi-directional lists are a.next =b, and there must be b.prev = a; but there is no such restriction on binary lists, which can point to any node).
Okay, let's do it now.
package Chap6; import java.util.ArrayList; import java.util.List; public class TreeChildSib<Item> { public static class Node<T> { private T data; private Node<T> nextChild; private Node<T> nextSib; public T getData() { return data; } public Node(T data) { this.data = data; } @Override public String toString() { String child = nextChild == null ? null : nextChild.getData().toString(); String sib = nextSib == null ? null : nextSib.getData().toString(); return "Node{" + "data=" + data + ", nextChild=" + child + ", nextSib=" + sib + '}'; } } private Node<Item> root; // Store all nodes, add in each new node private List<Node<Item>> nodes = new ArrayList<>(); private int nodesNum; // Initialize the tree with the specified root node public TreeChildSib(Item data) { setRoot(data); } // Empty parameter constructor public TreeChildSib() { } public void setRoot(Item data) { root = new Node<>(data); nodesNum++; nodes.add(root); } public void addChild(Item data, Node<Item> parent) { Node<Item> node = new Node<>(data); // If the parent is a leaf node, no child if (parent.nextChild == null) { parent.nextChild = node; // parent has children and can only be placed after the last brother of n's first child. } else { // From parent's first child, back to the last brother Node<Item> current = parent.nextChild; while (current.nextSib != null) { current = current.nextSib; } current.nextSib = node; } nodesNum++; nodes.add(node); } public List<Node<Item>> childrenFromNode(Node<Item> node) { List<Node<Item>> children = new ArrayList<>(); for (Node<Item> cur = node.nextChild; cur!= null; cur = cur.nextSib) { { children.add(cur); } } return children; } public Node<Item> parentTo(Node<Item> node) { for (Node<Item> eachNode : nodes) { if (childrenFromNode(eachNode).contains(node)) { return eachNode; } } return null; } public boolean isEmpty() { return nodesNum == 0; } public Node<Item> root() { return root; } public int nodesNum() { return nodesNum; } public int depth() { return nodeDepth(root); } public int nodeDepth(Node<Item> node) { if (isEmpty()) { return 0; } int max = 0; if (childrenFromNode(node).size() > 0) { for (Node<Item> child: childrenFromNode(node)) { int depth = nodeDepth(child); if (depth > max) { max = depth; } } } return max + 1; } public int degree() { int max= 0; for (Node<Item> node: nodes) { if (childrenFromNode(node).size() > max) { max = childrenFromNode(node).size(); } } return max; } public int degreeForNode(Node<Item> node) { return childrenFromNode(node).size(); } public void clear() { // Delete the actual tree postOrder(root); // Release storage nodes for (Node<Item> node: nodes) { node.nextSib = null; node.nextChild = null; node.data = null; } nodesNum = 0; } // Post-order traversal clears the information of each node private void postOrder(Node<Item> root) { if (root == null) { return; } postOrder(root.nextChild); postOrder(root.nextSib); root.nextChild = null; root.nextSib = null; root.data = null; } public static void main(String[] args) { TreeChildSib<String> tree = new TreeChildSib<>("A"); TreeChildSib.Node<String> root = tree.root(); tree.addChild("B", root); tree.addChild("C", root); tree.addChild("D", root); TreeChildSib.Node<String> child1 = tree.childrenFromNode(root).get(0); TreeChildSib.Node<String> child2 = tree.childrenFromNode(root).get(1); TreeChildSib.Node<String> child3 = tree.childrenFromNode(root).get(2); tree.addChild("E", child1); tree.addChild("F", child2); tree.addChild("G", child1); tree.addChild("H", child3); System.out.println(root); System.out.println("The number of nodes in the tree is"+tree.nodesNum()); System.out.println("The depth of the tree is"+tree.depth()); System.out.println("The degree of the tree is"+tree.degree()); System.out.println(child1.getData()+"Degree is"+tree.degreeForNode(child1)); System.out.println(child2.getData()+"The parent node is"+tree.parentTo(child2).getData()); tree.clear(); System.out.println(tree.root()); System.out.println(tree.isEmpty()); } } /* Outputs Node{data=A, nextChild=B, nextSib=null} The tree has 8 nodes. The depth of the tree is 3. The tree has a degree of 3. B The degree is 2. C The parent node is A [Node{data=B, nextChild=E, nextSib=C}, Node{data=C, nextChild=F, nextSib=D}, Node{data=D, nextChild=H, nextSib=null}] Node{data=null, nextChild=null, nextSib=null} true */
Because some methods need to traverse all the nodes of the tree, a table named List < Node < Item > nodes is built to store. Specifically, this node is added to the table every time a node is added.
The addChild method is very important. If the parent node that needs to be attached has no child (if branch), the node that needs to be added becomes its first child; if the parent node has a child (else branch), then it starts with the first child of the parent node and then the newly added node is located here after its last brother.
The childrenFromNode method is to start with the first child of the node and find his brother constantly. The first child and all his brothers are all the children of the node.
The algorithm of seeking degree and depth is similar to that of children's representation, so we will not elaborate on it any more. To see the method of clear ing the empty tree, we need to leave the information of each node empty. We must have a method to traverse the tree. Here we use the method of post-order traversal, which is not finished after that. The table storing the nodes should also be empty.
If you want to make it easier to get the parent node, you can also set up a parent field to see the children express the optimization of the method.
The child brothers'representation has an advantage that it can transform an ordinary tree into a binary tree. Because of the many characteristics of the binary tree, it is easy to deal with. The list above the child's brothers'representation can be changed into a binary tree by stretching slightly and changing the structure below, as follows.
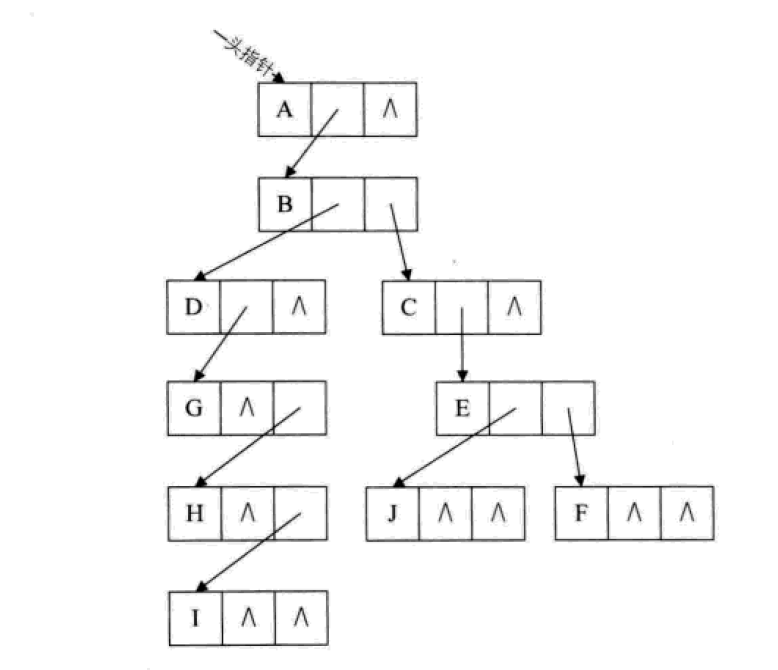
by @sunhaiyu
2017.9.8