1. Terms and marks of sorting
Sorting key: it can be any comparable data type (character, string, integer, real number, etc.).
For any record, you can find a function to get its key.
Stability: do not change the original input order of records with the same key.
2. The three costs are Θ (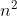
)Sorting method (insert, bubble, select)
I. insert sort: process the records to be sorted one by one, compare each new record with the previously sorted subsequence, and insert it into the correct position of the subsequence. The input is an array of records, in which n records are stored.
code:
// Insertion sort method
static int[] insertionsort(int[] array){
if (array.length>0){
for(int i=0;i<array.length;i++){
int current=array[i+1];
int index =i;
while (index>=0&& current<array[index]){
array[index+1]=array[index];
index--;
}
array[index+1]=current;
}
}
return array;
}The outer layer circulates n-1 times, and the inner layer needs n-1 times at the worst, so Θ (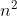)Worst, best Θ (n) , average Θ ()
.
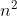Inverse: a number larger than a number in front of it. Each such number is called an inverse.
II bubble sort: double for loop. The inner loop compares the adjacent keys from the bottom of the array to the top of the array. If the following keys are smaller than the keys of their neighbors, they will be exchanged in order.
code:
static int[] bubblesort(int[] array){
if(array.length>0){
for (int i=0;i<array.length-1;i++){
for(int j=0;j<array.length-1-i;j++){
if (array[j]>array[j+1]){
int temp=array[j];
array[j]=array[j+1];
array[j+1]=temp;
}
}
}
}
return array;
}
}Double cycle, worst and average Θ (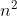), preferably Θ (n).
III. selective sorting: traverse the array, exchange the smallest element with the first element, then traverse the array, and exchange the smallest element with the second element. No exchange occurs during each traverse, and only after the end of the traverse.
code:
public int[] selctingsort(int[] array) {
for (int i=0;i<array.length;i++){
int minnum=i;
for (int j=i;j<array.length;j++){
if(array[j]<array[minnum]){
minnum=j;
}
}
if(minnum!=i){
int temp=array[i];
array[i]=array[minnum];
array[minnum]=temp;
}
}
return array;
}In any case, there must be a double cycle, even if there is no exchange, so the average is the best and worst Θ (n party).
The time cost of exchanging (exchanging adjacent records is called one-time exchange) sorting algorithm:
The key reason why the above three sorting algorithms run slowly is that they only compare adjacent elements, so the comparison and movement can only be carried out step by step. The average time cost of any exchange algorithm that limits the comparison to two adjacent elements is Θ (n party).
3.Shell sorting (reduced incremental sorting method)
In insertion sorting, if a small number is inserted, the number of times to move back significantly increases, which affects the efficiency, so it is necessary to find a new algorithm.
Description: divide the sequence into subsequences, then sort the subsequences respectively, and finally combine the subsequences. (try to turn the sequence to be arranged into an approximate sequence state, and then insert sorting to complete the final sorting)
1 in each cycle, the target sequence is divided into unconnected subsequences, and the spacing of elements in each subsequence in the whole array is the same (that is, subsequences are taken at the same interval and have the same length).
code:
1 -- exchange type (bubbling inside)
public int[] shellsort(int[] array){
int temp=0;
for(int gap=array.length;gap>0;gap=gap/2){
for (int i=gap;i<array.length;i++){
for (int j=i-gap;j>=0;j=j-gap){
if(array[j]>array[j+gap]){
temp=array[j];
array[j]=array[j+gap];
array[j+gap]=temp;
}
}
}
}
return array;
}
2 -- shift (insert inside) real Hill sort
public static int[] shellsort2(int[] arrary){
for (int gap=arrary.length/2;gap>0;gap/=2){
for (int i=gap;i<arrary.length;i++) {
int j = i;
int temp = arrary[j];
if (arrary[j] < arrary[j - gap]) {
while (j - gap >= 0 && temp < arrary[j - gap]) {
arrary[j] = arrary[j - gap];
j = j - gap;
}
arrary[j]=temp;
}
}
}
return arrary;
}The best average and worst are Θ (nlog2n).
4. Quick sort
Quick sort is an improvement of bubble sort. Select a benchmark number (axis number v) to divide the records to be arranged into two parts greater than the benchmark number and less than the benchmark number, and sort the left and right parts recursively.
code:
Realize one
public static int[] QuickSortv1(int[] array, int low, int hight) {
//if (array.length < 1 || low < 0 || hight >= array.length || low > hight) return null;
if (low < hight) {
int privotpos = partition(array, low, hight);
QuickSortv1(array, low, privotpos - 1);
QuickSortv1(array, privotpos + 1, hight);
}
return array;
}
//the method below is used in quicksort
public static int partition(int[] array, int low, int hight) {
int privot = array[low];
while (low < hight) {
while (low < hight && array[hight] >= privot) --hight;
array[low] = array[hight];
while (low < hight && array[low] <= privot) ++low;
array[hight] = array[low];
}
array[low] = privot;
return low;
}Realization 2:
public static int[] QuickSortv2(int[]array,int left,int right) {
int l = left;
int r = right;
int v = array[(left + right) / 2];
int temp = 0;
// the while block below aims to makes the smaller numbers put int the left and
//the larger put in the right (smaller or larger than the v value)
while (l < r) {
// search for the larger num from the left
while (array[l] < v) {
l += 1;
}
// search for the smaller num for the right
while (array[r] > v) {
r -= 1;
}
//if l>=r, meaning that nums on the left are all smaller or equal to v value
// and the nums on the right are all lager or equal to v value
if (l >= r) {
break;
}
//things are not always that good for us, so we need to do the swap to move the smaller to the left
// and the lager to the right.
temp = array[l];
array[l] = array[r];
array[r] = temp;
//if arr[l]==v after swapping, do r-- to move back;
if (array[l] == v) {
r -= 1;
}
//iff arr[r]==v after swapping, do l++ to move forward
if (array[r] == v) {
l += 1;
}
}
// if l==r, must do l++ and r--, or the stock will overflow
if(l==r){
l+=1;
r-=1;
}
// do the same sort on the left and right sub-array
if(left<r){
QuickSortv2(array,left,right);
}
if(right>1){
QuickSortv2(array,1,right);
}
return array;
}Analysis: the best case and average case are Θ (nlogn), the worst case is Θ (n party)
5. Merge and sort
Merge sort is based on divide and conquer method, which divides the element sequence to be sorted into two subsequences with equal length, sorts each subsequence, and then combines them into a subsequence. Merge sort is a stable sort algorithm, and the best and worst average cases are Θ (nlog2n)
First write a method to sort two subsequences: fill the left and right data into the temp array according to the rules until one side of the ordered sequence on the left and right is processed. Compare the first number of the left and right arrays from the left with the first number of the right array. If the number on the left is small, add it to the temp array, otherwise add it to the right array The number of is added to the array, and the left or right subscript and the subscript of temp are moved back to process the next bit. If there is remaining data at a time, all the remaining parts need to be filled into temp in turn (the judgment conditions are whether the left subscript is to mid and the right subscript is to right)
public static void merge(int[]arr,int left,int mid,int right){
int i=left;
int []temp=new int[arr.length];//Auxiliary array
int j=mid+1;
int t=0;//Points to the current index of the temp array
//First copy the left and right data into temp according to the rules until one side of the ordered sequence on the left and right is processed
while (i<=mid&&j<=right){
if (arr[i]<=arr[j]){
temp[t]=arr[i];
t+=1;
i+=1;
}else {
temp[t]=arr[j];
t+=1;
j+=1;
}
}
//Handle the number of unfilled left and right edges
while (i<=mid){
temp[t]=arr[i];
t=t+1;
i=i+1;
}
while (j<=right){
temp[t]=arr[i];
t+=1;
j+=1;
}
//After filling, copy all the elements in the temp array to the arr
for (int x = left; x <=right; x++){
arr[x]=temp[x];}
}
//Disassembly + closing
public static void mergeSort(int[]a ,int start,int end){
if(start<end){
int mid=(start+end)/2;
mergeSort(a,start,mid);
mergeSort(a,mid+1,end);
merge(a,start,mid,end);
}
}new temp is required for every call to merge, which causes a lot of time loss. After improvement, when int[] temp is passed into the function as a parameter, the time consumption will be greatly reduced when the amount of data is large enough. The improved version is shown below.
public static void merge(int[]arr,int left,int mid,int right,int[] temp){
int i=left;
int j=mid+1;
int t=0;//Points to the current index of the temp array
//First copy the left and right data into temp according to the rules until one side of the ordered sequence on the left and right is processed
while (i<=mid&&j<=right){
if (arr[i]<=arr[j]){
temp[t]=arr[i];
t+=1;
i+=1;
}else {
temp[t]=arr[j];
t+=1;
j+=1;
}
}
//Handle the number of unfilled left and right edges
while (i<=mid){
temp[t]=arr[i];
t=t+1;
i=i+1;
}
while (j<=right){
temp[t]=arr[i];
t+=1;
j+=1;
}
//After filling, copy all the elements in the temp array to the arr
t=0;
int tempLeft =left;
while (tempLeft<=right){
arr[tempLeft]=temp[t];
t+=1;
tempLeft+=1;
}
}
//Disassembly + closing
public static void mergeSort(int[]a ,int start,int end,int[] temp){
if(start<end){
int mid=(start+end)/2;
mergeSort(a,start,mid,temp);
mergeSort(a,mid+1,end,temp);
merge(a,start,mid,end,temp);
}
}6. Cardinality sorting
Cardinal sorting is an extension of bucket sorting. It is a stable sorting method. The basic idea is to sort bit by bit. Each number is divided into buckets, and its number is determined by the longest data of all data. Typically, space is used for time, which can not process massive data. It makes use of the relevant knowledge of stack.
Handle cardinality sorting of integer data:
public static void radixSort(int[] arr){
//Gets the maximum number of digits
int max=arr[0];
for (int i=1;i<arr.length;i++){
if (arr[i]>max){
max=arr[i];
}
}
int maxlength=(max+"").length();
//Define a two-dimensional array to represent ten buckets, and each bucket is a one-dimensional array. To prevent overflow, define the bucket size larger
int[][] bucket=new int[10][arr.length];
//Record how many data are actually stored in each bucket, define an array, and record the number of data put into each bucket each time
int[] bucketElementCounts =new int[10];
//Use loop processing code
for (int i=0,n=1;i<maxlength;i++,n*=10){
for (int j=0;j<arr.length;j++){
//Take out bit i+1
int digitOfElement=arr[j]/n%10;
//Put into the corresponding bucket
bucket[digitOfElement][bucketElementCounts[digitOfElement]]=arr[j];
bucketElementCounts[digitOfElement]++;
}
//Take out the data in the order of the bucket and put it into the original array
int index=0;
for(int k=0;k<bucketElementCounts.length;k++){
//If there is data in the bucket, it will be put into the original array
if (bucketElementCounts[k]!=0){
//Cycle the bucket to put data
for (int l=0;l<bucketElementCounts[k];l++){
arr[index]=bucket[k][l];
index++;
}
}
//After the i+1 round of processing, each bucket elementcounts [k] needs to be zeroed to store the next bit
bucketElementCounts[k]=0;
}
System.out.println("The first"+(i+1)+"Round, the sorting result of the array is"+Arrays.toString(arr));
}Processing cardinality sorting of strings: implementation of a
public static String[] stringradixSort(String[] strArr) {
if(strArr == null) {
return null;
}
int maxLength = 0; // Record only the maximum number of digits
// Get the maximum number of bits of the array first
for (String len : strArr) {
// Record only the maximum number of digits
if (len.length() >= maxLength) {
maxLength = len.length();
}
}
System.out.println("The maximum length of string in string cardinality sorting is: " + maxLength);
ArrayList<ArrayList<String>> buckets = null;
// Sort from the last letter
for (int i=maxLength-1; i>=0; i--) {
// Because there are only 26 English letters, it is declared that there are 26 barrels
buckets = new ArrayList<ArrayList<String>>();
for (int b = 0; b < 27; b++) {
buckets.add(new ArrayList<String>());
}
// Sorting mainly needs to consider the capacity of buckets. For example, the array is 10 buckets and the letters are 26 buckets
for (String str : strArr) {
buckets.get(getStrIndex(str, i)).add(str);
}
// Reassign
int index = 0;
for (ArrayList<String> bucket : buckets) {
for (String str : bucket) {
strArr[index++] = str;
}
}
}
return strArr;
}
public static int getStrIndex(String str, int charIndex) {
if (charIndex >= str.length()) {
return 0; // Non alphabetic case in the 0th bucket
}
int index = 26; // 26 letters in total
int n = (int) str.charAt(charIndex); // Cast letters into numbers
if (64 < n && n < 91) { // Upper case range
index = n - 64;
} else if (96 < n && n < 123) { // Lowercase letter range
index = n - 96;
} else {
// Put the rest of the non letters last
index = 26;
}
return index;
}Realization 2:
public static String[] sorting(String[] strings)
{
//Find the maximum length in the string as the number of cycles
int max = 0;//Maximum
for (String string : strings) {
if (string.length()>max)
{
max = string.length();
}
}
int a = 1;//The subscript used to calculate which bit to get
//Create data bucket
List<List<String>>listList = null;//Assign null first, because the data in the bucket needs to be emptied every cycle
//Start sorting
for (int i = 0; i <=max-1; i++) { //How many cycles
listList = new ArrayList<>();//Each cycle refreshes the list set again
//Create 27 data buckets
for (int k = 0; k<27; k++) {
listList.add(new ArrayList<>());
}
//Store the sorted data in the data bucket
for (String string : strings) {
listList.get(getint(string,string.length()-a)).add(string);//string.length()-a so that the uniform subscript position of each digit can be obtained
}
a++;
//Present data
int index = 0;
for (List<String> stringList : listList) {
for (String s : stringList) {
strings[index++] = s;
}
}
}
return strings ;
}
//Get the data pass position of each letter
public static int getint(String s,int i){
if(i<0)
//If the subscript is out of bounds, it will directly return 0, because it is the longest string to determine the number of cycles and subscripts.
// In this way, long subscripts will be used to obtain short ones, and an error will be reported if they are not obtained. The subscript is out of bounds
{
return 0;
}
int a =s.charAt(i);//Gets the position in the ASCll table according to the character
if (a>64&&a<91)
{
return a-64;
}
else if (a>96&&a<123)
{
return a-96;//-96 can get the position of the data bucket. If it is a, its position in the ASCll table is 97,
//Then 1 is put into the data bucket with subscript 1
}
return 0;
}
The above two sorts can handle strings with different lengths. The comparison is sorted according to bit dictionary order ascii code.
Comparison:
The heap sort will be updated after the author completes the learning related to the tree