Data structure - Application of stack and queue I

Application of stack in recursion

The essence of recursion is whether the original problem can be transformed into a smaller problem with the same attributes.

• Features of function call: the last called function ends first (LIFO).
• When calling a function, you need to use a stack to store:
  ① Call return address
  ② Argument
  ③ Local variable
• It must be noted that the recursive model cannot be loop defined. It must meet the following two conditions:
  ① Recursive expression (recursive body)
  ② Boundary conditions (recursive exit)

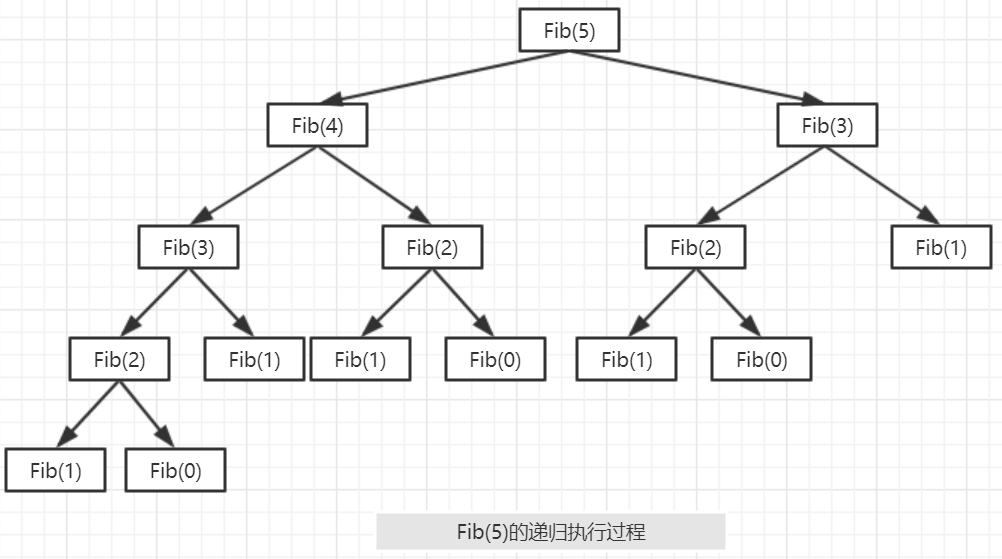
Fibonacci series:
F i b ( n ) { F i b ( n − 1 ) + F i b ( n − 1 ) ， n > 1 1 ， n = 1 0 ， n = 0 Fib(n)\begin{cases} Fib(n-1)+Fib(n-1)，n>1\\ 1，n=1\\ 0，n=0 \end{cases} \\ Fib(n)⎩⎪⎨⎪⎧​Fib(n−1)+Fib(n−1)，n>11，n=10，n=0​

int Fib(int n) //Implementation of Fibonacci sequence
{
	if (n == 0) return 0; //boundary condition 
	else if (n == 1) return 1; //boundary condition 
	else return Fib(n - 1) + Fib(n - 2); //Recursive expression
}

Factorial:
f a c t o r i a l ( n ) { n × f a c t o r i a l ( n − 1 ) ， n > 1 1 ， n = 1 1 ， n = 0 factorial (n)\begin{cases} n×factorial(n−1) ，n>1\\ 1，n=1\\ 1，n=0 \end{cases} \\ factorial(n)⎩⎪⎨⎪⎧​n×factorial(n−1)，n>11，n=11，n=0​

int factorial(int n) //Realization of factorial
{
	if (n == 0 || n == 1) return 1; //boundary condition 
	else return n*factorial(n-1); //Recursive expression
}

A stack is used to realize the non recursive calculation of the following recursive functions:
P n ( x ) { 2 x P n − 1 ( x ) − 2 ( n − 1 ) P n − 2 ( x ) ， n > 1 2 x ， n = 1 1 ， n = 0 P_n(x)\begin{cases} 2xP_{n-1}(x)-2(n-1)P_{n-2}(x) ，n>1\\ 2x，n=1\\ 1，n=0 \end{cases} \\ Pn​(x)⎩⎪⎨⎪⎧​2xPn−1​(x)−2(n−1)Pn−2​(x)，n>12x，n=11，n=0​

Algorithm implementation

• Algorithm idea: set a stack to save n and the corresponding P n ( x ) P_n(x) Pn (x) value, find the value of adjacent elements in P n ( x ) P_n(x) Pn (x) has the relationship between questions. Then calculate while out of the stack P n ( x ) P_n(x) Pn (x), this value is calculated when the stack is empty.

#include<stdio.h>
#define MaxSize 100
double recursion(int n, double x)
{
	struct stack
	{
		int no;
		double val;
	}St[MaxSize];
	int top = -1, i;
	double fv1 = 1, fv2 = 2 * x;
	for (i = n; i >= 2; i--)
	{
		top++;
		St[top].no = i;
	}
	while (top >= 0)
	{
		St[top].val = 2 * x * fv2 - 2 * (St[top].no - 1) * fv1;
		fv1 = fv2;
		fv2 = St[top].val;
		top--;
	}
	if (n == 0) return fv1;
	return fv2;
}

int main()
{
	printf("%lf", recursion(4, 3.2));
	return 0;
}

//Output result: 1198.201600

Application of stack in maze problem

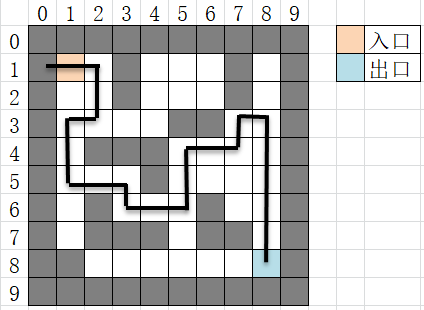
• Given an M × N, find a maze path from the specified entrance to the exit. Suppose a maze diagram (here M=8,N=8), in which each square represents the channel with blank and the obstacle with shadow. In general, the maze path is a simple path, that is, there will be no blocks on the maze path. There may be more than one maze path in a maze diagram. These maze paths are long and short. Here, we only consider using the stack to find a maze path from the specified entrance to the exit.

• Algorithm idea: in order to represent the maze, set up an array mg [], in which each element represents the state of a block. When it is 0, it means that the corresponding block is a channel, and when it is 1, it means that the corresponding block is an obstacle (non walkable). For the convenience of the algorithm, a fence is generally added around the fan official. (since a fence is added around the maze, the number of rows and columns of Mg array are added with 2)
  

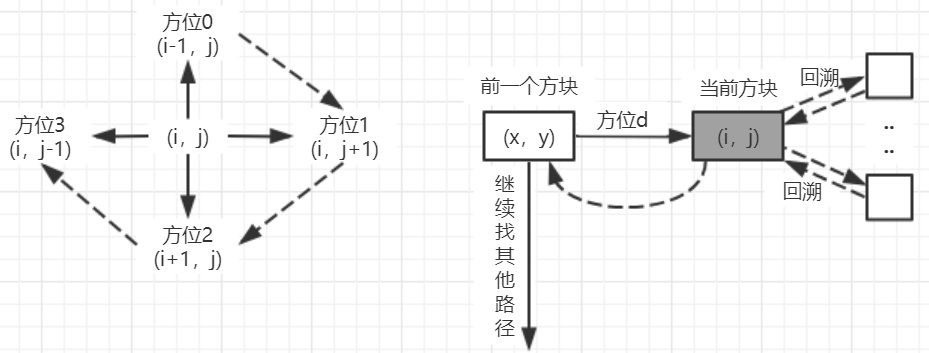
Algorithm implementation:

#include<iostream>
using namespace std;
#include<malloc.h>
#define MaxSize 200
#define M 8
#define N 8
typedef struct Box
{
	int i; //The line number of the current box
	int j; //The column number of the current box
	int di; //di is the bearing number of the next adjacent walkable bearing
};
typedef struct StType
{
	Box data[MaxSize];
	int top;
};

bool InitStack(StType*& S)
{
	S = (StType*)malloc(sizeof(StType)); //Allocate a sequential stack space, and store the first address in s
	if (S == NULL) return false; //Insufficient memory, allocation failed
	S->top = -1; //The stack top pointer is set to - 1
	return true;
}

bool StackEmpty(StType* S)
{
	return S->top == -1;
}

bool Push(StType*& S, Box x)
{
	if (S->top == MaxSize - 1) return false; //When the stack is full, that is, overflow on the stack
	S->top++; //Stack top pointer increases by 1
	S->data[S->top] = x; //The element x is placed at the pointer at the top of the stack
	return true;
}

bool Pop(StType*& S, Box& x)
{
	if (S->top == -1) return false; //The stack is empty, that is, overflow under the stack
	x = S->data[S->top]; //Get stack top element
	S->top--; //Stack top pointer minus 1
	return true;
}

bool GetTop(StType* S, Box& x)
{
	if (S->top == -1) return false; //The stack is empty, that is, overflow under the stack
	x = S->data[S->top]; //Get stack top element
	return true;
}

void DestoryStack(StType*& S) //Destroy stack
{
	free(S);
}

bool mgpath(int xi, int yi, int xe, int ye) //The solution path is (xi, yi) → (xe, ye)
{
	int mg[M + 2][N + 2] = { {1,1,1,1,1,1,1,1,1,1},{1,0,0,1,0,0,0,1,0,1},
											{1,0,0,1,0,0,0,1,0,1},{1,0,0,0,0,1,1,0,0,1},
											{1,0,1,1,1,0,0,0,0,1},{1,0,0,0,1,0,0,0,1},
											{1,0,1,0,0,0,1,0,0,1},{1,0,1,1,1,0,1,1,0,1},
											{1,1,0,0,0,0,0,0,0,1},{1,1,1,1,1,1,1,1,1,1} };
	Box path[MaxSize], e;
	int i, j, di, i1, j1, k;
	bool find;
	StType* st; //Define stack st
	InitStack(st); //Initialize stack top pointer
	e.i = xi; e.j = yi; e.di = -1; //Set e as entrance
	Push(st, e); //Block e stack
	mg[xi][yi] = -1; //Set the maze value of the entrance to - 1 to avoid going to the box repeatedly
	while (!StackEmpty(st)) //Loop when stack is not empty
	{
		GetTop(st, e); //Stack top block e
		i = e.i; j = e.j; di = e.di;
		if (i == xe && j == ye) //The exit is found and the path is output
		{
			printf("A maze path is as follows:\n");
			k = 0;
			while (!StackEmpty(st))
			{
				Pop(st, e); //Stack out box e
				path[k++] = e; //Add e to the path array
			}
			while (k >= 1)
			{
				k--;
				printf("\t(%d,%d)", path[k].i, path[k].j);
				if ((k + 1) % 5 == 0) printf("\n"); //Change a line after every 5 blocks are output
			}
			printf("\n");
			DestoryStack(st); //Destroy stack
			return true; //Return true after outputting a maze path
		}
		find = false;
		while (di < 4 && !find)
		{
			di++; //Find the next adjacent walkable block (i1, j1) of block (i,j)
			switch (di)
			{
			case 0: i1 = i - 1; j1 = j; break;
			case 1: i1 = i; j1 = j + 1; break;
			case 2: i1 = i + 1; j1 = j; break;
			case 3: i1 = i; j1 = j - 1; break;
			}
			if (mg[i1][j1] == 0) find = true; //Find an adjacent walkable box and set find to true
		}
		if (find) //An adjacent walkable block (i1,j1) was found
		{
			st->data[st->top].di = di; //Modify the di value of the original stack top element
			e.i = i1; e.j = j1; e.di = -1;
			Push(st, e); //Adjacent walkable blocks e into the stack
			mg[i1][j1] = -1; //Set the maze value of (i1,j1) to 1 to avoid going to the box repeatedly
		}
		else //If there is no path to go, it will be returned to the stack
		{
			Pop(st, e); //Return the stack top box to the stack
			mg[e.i][e.j] = 0; //Change the position of the back stack box to another path available box
		}
	}
	DestoryStack(st); //Destroy stack					
	return false; //Indicates that there is no path to go, and returns false
}

int main()
{
	if (!mgpath(1, 1, M, N)) printf("The maze problem has no solution!");
	return 0;
}

Program analysis:

• Operation results:
  
  

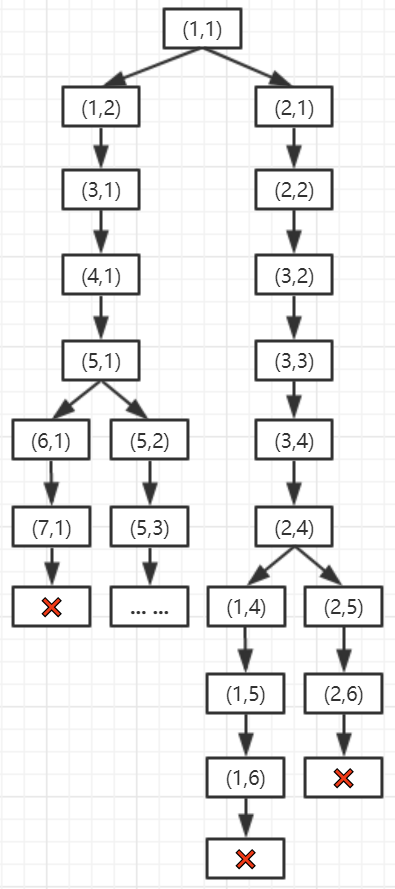
Application of queue in maze problem

• Algorithm idea: starting from the entrance (xi,yi), using the characteristics of the queue, expand outward layer by layer to find the walkable box until the exit is found. This method is the breadth first search method.

Algorithm implementation:

//Solving maze problem with queue
#include <stdio.h>
#include <malloc.h>
#define MaxSize 100
#define M 8
#define N 8
int mg[M + 2][N + 2] = { {1,1,1,1,1,1,1,1,1,1}, {1,0,0,1,0,0,0,1,0,1},
						 {1,0,0,1,0,0,0,1,0,1}, {1,0,0,0,0,1,1,0,0,1},
						 {1,0,1,1,1,0,0,0,0,1}, {1,0,0,0,1,0,0,0,0,1},
						 {1,0,1,0,0,0,1,0,0,1}, {1,0,1,1,1,0,1,1,0,1},
						 {1,1,0,0,0,0,0,0,0,1}, {1,1,1,1,1,1,1,1,1,1} };

typedef struct 
{
	int i, j; //Position of the box
	int pre;	//The subscript of the previous block in this path in the queue
} Box; //block type 
typedef struct
{
	Box data[MaxSize];
	int front, rear; //Queue head pointer and queue tail pointer
} QuType; //Sequential team type


void InitQueue(QuType *&q) //Initialize queue
{	q=(QuType *)malloc (sizeof(QuType));
	q->front = q->rear = -1;
}
void DestroyQueue(QuType *&q)	 //Destroy queue
{
	free(q);
}
bool QueueEmpty(QuType *q) //Determine whether the queue is empty
{
	return(q->front == q->rear);
}
bool enQueue(QuType*& q, Box e) //Enter queue
{	
	if (q->rear==MaxSize-1)	return false; //Overflow when the team is full, return false
	q->rear++; //Team tail increased by 1
	q->data[q->rear] = e; //Insert element e at the rear position
	return true; //Return true
}
bool deQueue(QuType*& q, Box& e) //Out of queue
{	if (q->front==q->rear)	return false; //Team under air overflow
	q->front++;
	e = q->data[q->front];
	return true;
}

void print(QuType* qu, int front) //Output path from queue qu
{
	int k = front, j, ns = 0;
	printf("\n");
	do	 //Reversely find the shortest path and set the pre member of the box on the path to - 1
	{	
		j=k;
		k = qu->data[k].pre;
		qu->data[j].pre = -1;
	} while (k != 0);
	printf("A maze path is as follows:\n");
	k=0;
	while (k < MaxSize) //Forward search to the box with pre - 1, that is, the path forming the forward direction
	{	
		if (qu->data[k].pre==-1)
		{	ns++;
			printf("\t(%d,%d)", qu->data[k].i, qu->data[k].j);
			if (ns % 5 == 0) printf("\n");	//Change one line after every 5 squares for each output
		}
		k++;
	}
	printf("\n");
}
bool mgpath1(int xi,int yi,int xe,int ye)	//The search path is: (Xi, Yi) - > (Xe, ye)
{
	Box e;
	int i, j, di, i1, j1;
	QuType *qu;	 //Define sequence queue pointer qu
	InitQueue(qu); //Initialize queue qu
	e.i = xi; e.j = yi; e.pre = -1;
	enQueue(qu,e); //(xi,yi) join the team
	mg[xi][yi] = -1; //Assign it - 1 to avoid repeating the search back
	while (!QueueEmpty(qu))	//Queue not empty and circular
	{	
		deQueue(qu, e); //Out of queue Block e, because it is not a ring queue, the out of queue element is still in the queue
		i = e.i; j = e.j;
		if (i==xe && j==ye) //Exit found, output path
		{	
			print(qu, qu->front);	//Call the print function to output the path
			DestroyQueue(qu); //Destroy queue
			return true; //Returns true when a path is found
		}
		for (di = 0; di < 4; di++) //Cycle through each orientation and insert each walkable block into the queue
		{	
			switch(di)
			{
			case 0:i1=i-1; j1=j;   break;
			case 1:i1=i;   j1=j+1; break;
			case 2:i1=i+1; j1=j;   break;
			case 3:i1=i;   j1=j-1; break;
			}
			if (mg[i1][j1]==0)
			{
				e.i = i1; e.j = j1;
				e.pre = qu->front;	//Subscript to the previous box in the path
				enQueue(qu, e); //(i1,j1) square into the team
				mg[i1][j1] = -1; //Assign it - 1 to avoid repeating the search back
			}
		}
     }
	DestroyQueue(qu); //Destroy queue
	return false; //Returns false if no path is found
}

int main()
{
	mgpath1(1,1,M,N);
	return 0;
}

Program analysis:

• The sequential queue qu used here is not a ring queue, because when finding the exit, you need to use all the blocks in the queue to find a maze path. If a ring queue is used, the blocks out of the team may be covered by the blocks in the new team, so it is impossible to find the maze path. It is required that the non ring queue qu has enough space.
• Operation results:
  
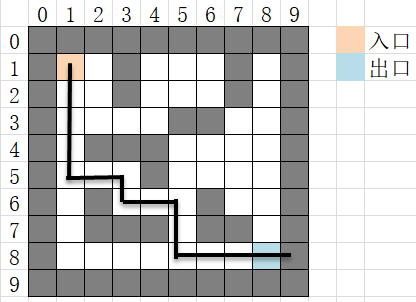
• Obviously, this solution is the optimal solution, that is, the shortest path.

Application of queue in computer system

• 1. Solve the problem of speed mismatch between host and external equipment

• Take the speed mismatch between the host and the printer as an example.
  The host outputs data to the printer for printing. The speed of outputting data is much faster than that of printing data. Due to the speed mismatch, it is obviously impossible to directly send the output data to the printer for printing. The solution is to set a print data buffer. The host writes the data to be printed into the buffer in turn. When it is full, it pauses the output and turns to do other things. The printer takes out the data from the buffer according to the principle of first in first out and prints. After printing, it sends a request to the host. After receiving the request, the host writes the print data to the buffer. This not only ensures the correctness of print data, but also improves the efficiency of the host. Thus, the data stored in the print data buffer is a queue.

• 2. Solve the problem of resource competition caused by multiple users

• The competition of CPU (central processing unit, which includes arithmetic unit and controller) resources is a typical example.
  On a computer system with multiple terminals, multiple users need the CPU to run their own programs, and they respectively request the operating system to occupy the CPU through their respective terminals. The operating system usually follows the chronological order of each request
  Order, arrange them into a queue, and allocate the CPU to the user requesting at the head of the queue each time. When the corresponding program runs out or runs out of the specified time interval, make it out of the queue, and then allocate the CPU to the user requested by the new head of the queue. This can not only meet the request of each user, but also make the CPU run normally.