preface

First, let's think about an ordinary binary tree to save data. If you want to find a data, because the ordinary binary tree to save data is random, the time complexity to find the data is O(n). Back for convenience
，We also learn the binary search tree. Its definition is to put the number smaller than the root node on the left and the number larger than the root node on the right, and each sub tree is a binary search tree, so that the data is stored in the tree
 Under certain circumstances, it is very convenient to find. However, when the order of data given is different, the binary search tree will be different. For example, if the given sequence is{1，2，3，4，5}or
{3，2，1，4，5}Two binary search trees will be different, and the search efficiency will be different.

We know that the search efficiency of a tree is related to the height of the tree. Of course, the best tree structure is full binary tree or complete binary tree. We call this kind of tree balanced. We know that binary search tree can achieve good search efficiency under certain circumstances. However, in general, the node insertion order of binary search tree can not be determined in advance. During dynamic search (deletion and insertion at the same time), the number structure will always change, which can not be balanced. Therefore, we need to consider how to ensure that the binary search tree can not only complete dynamic search, but also maintain a perfect tree structure. In this way, we have two problems to consider: one is the standard, what kind of tree is a tree with good tree structure, and the other is the balanced treatment and how to achieve the balance.

I definition

Balanced binary tree AVL tree(Named after the two mathematicians who invented it)，It is still a binary search tree, so it has all the properties of a binary search tree, just adding"balance"Limitations.
If the balanced binary tree is not an empty tree or a non empty binary search tree with the following conditions:
1. The absolute value of the height difference between the left and right subtrees cannot exceed 1(Balance factor, equivalent to a standard). 
2. The left and right subtrees are still a balanced binary tree.
With the definition of balance factor, we can find out the unbalanced tree, and then balance it. The specific contents are as follows. After treatment, the height of the tree can be maintained at O(logn)Level, so that
 The time complexity of the lookup operation is O(logn).

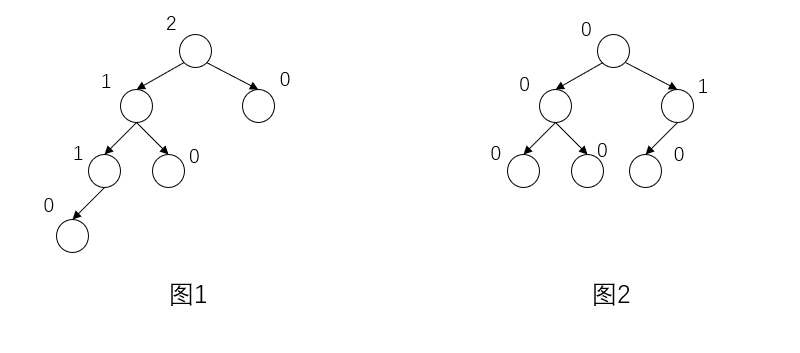
Figure 1 and Figure 2 are the values of the balance factor on the circle. It is obvious that figure 1 is not a balanced binary tree, and the balance factor of one point exceeds 1. Figure 2 is a balanced binary tree.

II basic operation

1. Find and delete

Since the balanced binary tree is still a binary search tree, its deletion and search operations will not increase the balance factor, so the operation is the same as that of the binary search tree. Visible blog: Binary search tree Find and delete.

2. Insert (how to adjust)

How to adjust

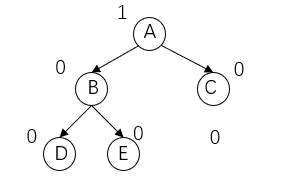
Suppose there is a balanced binary tree: (the top represents the balance factor)

LL type
When A node is inserted into the left or right subtree of D, the balance structure of the original balanced binary tree is destroyed, as shown in the figure: at this time, the balance factor of node A exceeds 1. We call node A the problem finding node and hexagonal star the problem generating node.

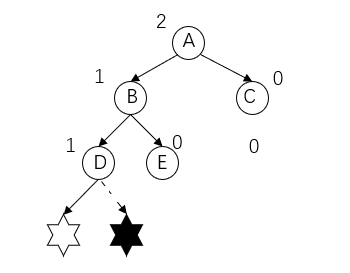
At this time, we need to look at the three consecutive nodes on the path of discovering the problem node and generating the problem node, starting from the discovery of the problem node. Enter a - > b - > D in the above figure. We find that these three nodes are on the left subtree of the left subtree of the problem node A. we call this imbalance as LL type (tilt left) imbalance.
How to adjust, the adjustment strategy of LL imbalance mainly rotates these three nodes (A,B,D) clockwise, and it is still a binary search tree.
Due to the nature of binary search tree:

1. Turn the right subtree of node B into the left subtree of A. (the left subtree of B is larger than B and smaller than a)
2. Let A be the right subtree of B (A is larger than B)
3. Set the root node to B
   
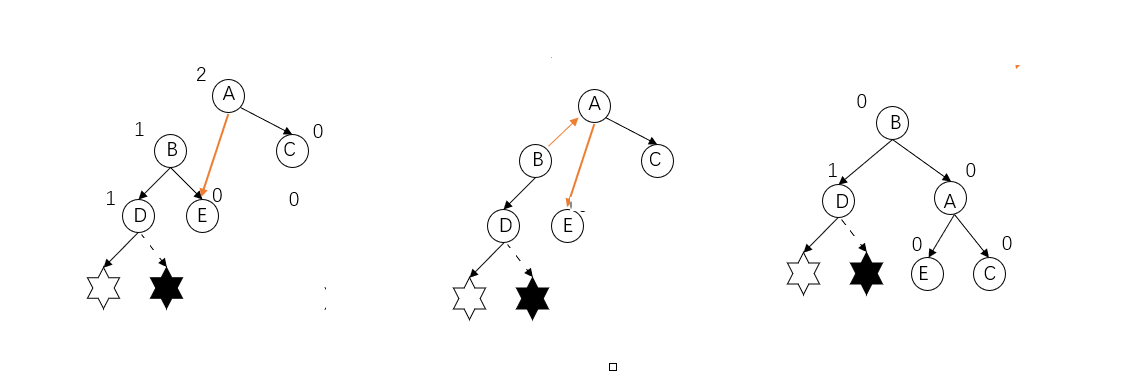
   Obviously, only the nodes on the path from the root node to the insertion node will change the balance factor. Therefore, only the unbalanced nodes on this path need to be adjusted, and only the unbalanced nodes closest to the insertion node need to be adjusted to normal, and all nodes on the path will be balanced. Therefore, the node that finds the problem is not necessarily the root node
   Note: it looks at the direction of three consecutive nodes from the discovery of the problem node to the generation of the problem node, and determines what type it is. And mainly adjust these three nodes.
   The code is as follows:

void SigelleftCir(Bactree **tree){//LL rotation
	Bactree *temp = NULL;
	temp = (*tree)->left;
	(*tree)->left = temp->right;
	temp->right = (*tree);
	(*tree)->hight = (GetHight((*tree)->left) > GetHight((*tree)->right) ? GetHight((*tree)->left) : GetHight((*tree)->right)) + 1;//After adjustment, keep the height of each node correct.
	temp->hight = (GetHight(temp->left) > GetHight(temp->right) ? GetHight(temp->left) : GetHight(temp->right)) + 1;
	(*tree) = temp; //Assign a value to (* tree), otherwise temp is the correct tree

}

RR type
The processing method of RR type is similar to that of LL type, as shown in the figure:

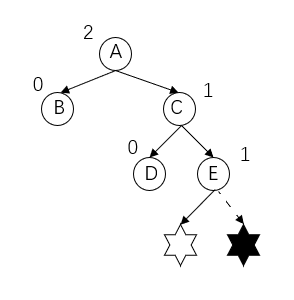
The problem node is the hexagonal star node (insert the left or right subtree of E), and it is found that the problem node is node A. The three consecutive nodes on the path from the discovery of the problem node are (A,C,E) nodes, which are respectively on the right subtree of the right subtree of the discovery problem node, so it is RR type (inclined to the right) imbalance.
Adjustment method: mainly rotate the three nodes (A,C,E) counterclockwise, and still be a binary search tree.

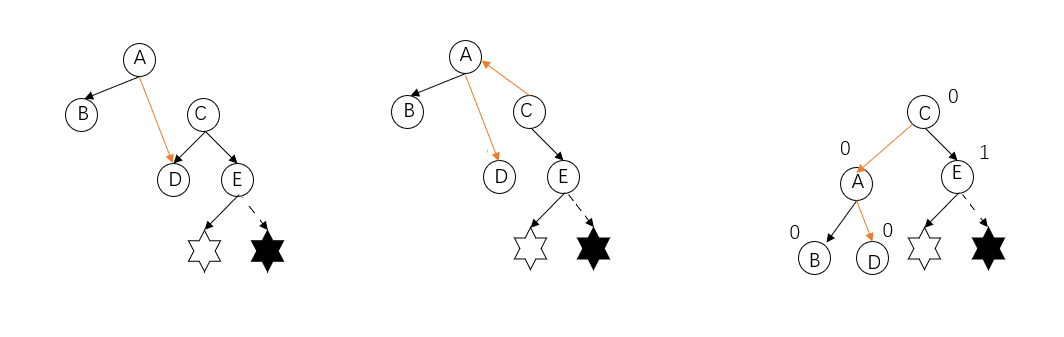
1. Turn the left subtree of node C into the right subtree of A.
2. Let A be the left subtree of C
3. Set the root node to C
   

void SigelrightCir(Bactree **tree){//RR rotation, same as LL
	Bactree *temp = NULL;
	temp = (*tree)->right;
	(*tree)->right = temp->left;
	temp->left = (*tree);
	(*tree)->hight = (GetHight((*tree)->left) > GetHight((*tree)->right) ? GetHight((*tree)->left) : GetHight((*tree)->right)) + 1;
	temp->hight = (GetHight(temp->left) > GetHight(temp->right) ? GetHight(temp->left) : GetHight(temp->right)) + 1;
	(*tree) = temp;

LR type

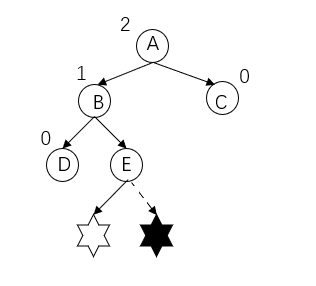
The problem node is hexagonal star (insert the left or right subtree of E), and it is found that the problem node is node A. The three consecutive nodes on the path from the discovery of the problem node are (A,B,E) nodes, which are respectively on the right subtree of the left subtree of the discovery problem node, so it is LR type imbalance.
Adjustment method: "left right double rotation", mainly rotate node B counterclockwise (left rotation) as the root node, and then rotate node A clockwise (right rotation) as the root node. (white hexagonal star is inserted in the drawing)

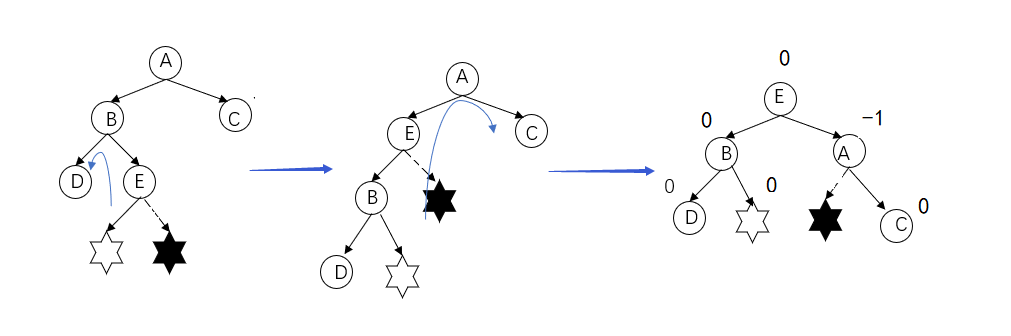
The code implementation adjustment of LR type is very simple, first right rotation, and then left rotation

void LeftrightCir(Bactree **tree){//LR rotation
	SigelrightCir(&((*tree)->left));
	SigelleftCir(tree);
}

RL type

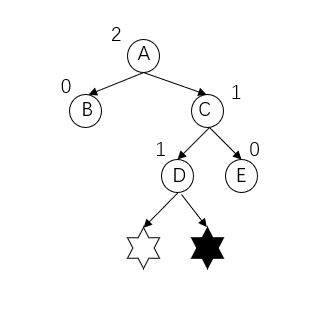
The problem node is hexagonal star (insert the left subtree or right subtree of D), and it is found that the problem node is node A. The three consecutive nodes on the path from the discovery of the problem node are (A,C,D) nodes, which are respectively on the left subtree of the right subtree of the discovery problem node, so it is RL type imbalance.
Adjustment method: "right left double rotation" mainly rotates clockwise (right rotation) with node C as the root node, and then rotates counterclockwise (left rotation) with node A as the root node. (white hexagonal star is inserted in the drawing)

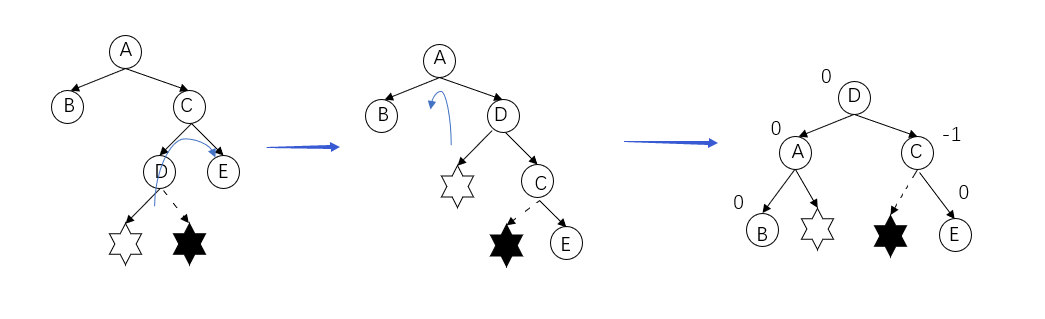
The code implementation is very simple to adjust RL type. First rotate left and then rotate right

void RightleftCir(Bactree **tree){//RL rotation
	SigelleftCir(&((*tree)->right));
	SigelrightCir(tree);
}

Code implementation insertion

#include<stdio.h>
#include<stdlib.h>
#include<Windows.h>
#pragma warning(disable:4996)

typedef int Elementtype;
typedef struct Balacetree{//Binary tree information
	Elementtype val;
	int hight;
	struct Balacetree *left;
	struct Balacetree *right;

}Bactree;


Bactree *TreeNodeCreate(Elementtype x){//Create tree node
	Bactree *tree = (Bactree *)malloc(sizeof(Bactree));
	tree->val = x;
	tree->hight = 1;
	tree->left = NULL;
	tree->right = NULL;
	return tree;
}

int GetHight(Bactree *tree){//Find tree height
	if (!tree){
		return 0;
	}
	int H;
	int LH;
	int RH;
	LH = GetHight(tree->left);
	RH = GetHight(tree->right);
	H = LH > RH ? LH : RH;
	return H + 1;
}
void SigelleftCir(Bactree **tree){//LL rotation
	Bactree *temp = NULL;
	temp = (*tree)->left;
	(*tree)->left = temp->right;
	temp->right = (*tree);
	(*tree)->hight = (GetHight((*tree)->left) > GetHight((*tree)->right) ? GetHight((*tree)->left) : GetHight((*tree)->right)) + 1;//After adjustment, keep the height of each node correct.
	temp->hight = (GetHight(temp->left) > GetHight(temp->right) ? GetHight(temp->left) : GetHight(temp->right)) + 1;
	(*tree) = temp; //Assign a value to (* tree), otherwise temp is the correct number

}
void SigelrightCir(Bactree **tree){//RR rotation, same as LL
	Bactree *temp = NULL;
	temp = (*tree)->right;
	(*tree)->right = temp->left;
	temp->left = (*tree);
	(*tree)->hight = (GetHight((*tree)->left) > GetHight((*tree)->right) ? GetHight((*tree)->left) : GetHight((*tree)->right)) + 1;
	temp->hight = (GetHight(temp->left) > GetHight(temp->right) ? GetHight(temp->left) : GetHight(temp->right)) + 1;
	(*tree) = temp;

}

void LeftrightCir(Bactree **tree){//LR rotation
	SigelrightCir(&((*tree)->left));
	SigelleftCir(tree);
}
void RightleftCir(Bactree **tree){//RL rotation
	SigelleftCir(&((*tree)->right));
	SigelrightCir(tree);
}

Bactree *BalaceTreePush(Bactree **tree, Elementtype x){
	if (!(*tree)){     //Insert Knot 
		*tree=TreeNodeCreate(x);
		return *tree;
	}
	if ((*tree)->val > x){  //x small insert left
		(*tree)->left = BalaceTreePush(&((*tree)->left), x);//Look to the right and return the node to the left pointer
		//Why put it in the loop? Put it in the loop to confirm a direction, which is the left
		if (GetHight((*tree)->left) - GetHight((*tree)->right) >= 2){//Balance factor
			if ((*tree)->left->val > x){//Confirmed the second direction to the left
				SigelleftCir(tree);//LL
			}
			else{//right
				LeftrightCir(tree);//LR
			}
		}
	}
	else{
		(*tree)->right = BalaceTreePush(&((*tree)->right), x);
		if (GetHight((*tree)->left) - GetHight((*tree)->right) <= -2){//Note - 2
			if ((*tree)->right->val < x){
				SigelrightCir(tree);
			}
			else{
				RightleftCir(tree);
			}
		}
	}
	(*tree)->hight = (GetHight((*tree)->left) > GetHight((*tree)->right) ? GetHight((*tree)->left) : GetHight((*tree)->right)) + 1;//Update height
	return *tree;

}

void Print(Bactree *tree){
	if (tree){
		Print(tree->left);
		printf("%d ", tree->val);
		Print(tree->right);
	}
}


int main(){
	Bactree *T = NULL;
	BalaceTreePush(&T, -10);
	BalaceTreePush(&T, -3);
	BalaceTreePush(&T, 0);
	BalaceTreePush(&T, 5);
	BalaceTreePush(&T, 9);
	BalaceTreePush(&T, 10);
	Print(T);

	system("pause");
	return 0;
}