Previous article: Data structure | tree and binary tree
Liu Dayou, textbook structure
Programming language: C++
catalogue
(1) Storage structure of binary tree
Root first traversal recursive algorithm
Root first traversal non recursive algorithm
Middle root traversal recursive algorithm
Middle root traversal non recursive algorithm
Back root traversal recursive algorithm
Back root traversal non recursive algorithm
(1) Storage structure of binary tree
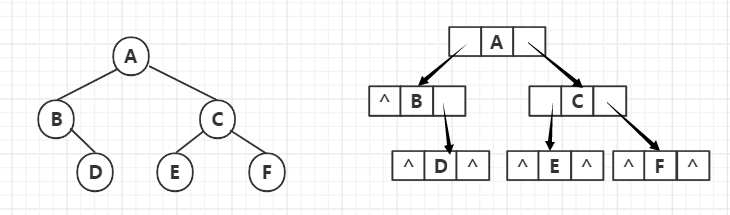
Binary tree has two storage modes in computer: sequential storage and chain storage. In the algorithms discussed in this paper, binary trees are stored in binary linked list
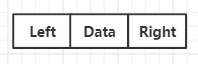
struct Node{
Node *Left;
Node *Right;
char Data;
};Left is used to save the pointer to the left son of the node, and Right is used to save the pointer to the Right son of the node
(2) Traversal of binary tree
Before learning to create a binary tree, we might as well learn the traversal of the binary tree, because the creation of the binary tree can be completed with the help of the traversal algorithm of the binary tree
The node sequence obtained by traversing the binary tree with the first root (middle root, later root and hierarchy) is called the first root order (middle root, later root and hierarchy) column
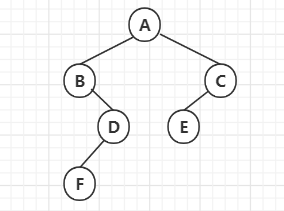
For example, for the binary tree shown in the following figure, its
- The first root sequence is ABDFCE
- The middle root sequence is BFDAEC
- The last root sequence is FDBECA
- The hierarchical sequence is ABCDEF
1. First root traversal
The steps are: ① access the root, ② traverse the left subtree, and ③ traverse the right subtree
Root first traversal recursive algorithm
/*preorder traversal */
void preOrder(Node * root){
//Recursive exit
if(root==nullptr)
return;
//Access root
cout<<root->data;
//Traverse left subtree
preOrder(root->left);
//Traversing right subtree
preOrder(root->right);
}
Root first traversal non recursive algorithm
#include <iostream>
using namespace std;
struct Node{
Node *left;
Node *right;
char data;
Node():left(nullptr),right(nullptr),data('#'){}
};
//Stack
class Stack{
public:
Stack():top(0){
for(int i=0;i<s_size;i++){
s[i]=nullptr;
}
}
//Push
void push(Node *p){
if(top<s_size){
s[top]=p;
top++;
}else{
cout<<"Stack overflow!"<<endl;
return;
}
}
//Out of stack
Node *pop(){
if(top==0){
return nullptr;
}else{
top--;
return s[top];
}
}
bool isEmpty(){
if(top==0)
return true;
else
return false;
}
private:
const int s_size=20;
Node *s[20];
int top;
};
/*Root first traversal non recursive algorithm*/
void nPreOrder(Node * root){
if(root == nullptr){
return;
}
Stack s;
Node *p=root;
//Root node stack
s.push(p);
//When stack is not empty:
while(!s.isEmpty()){
//Bullet stack:
p=s.pop();
cout<<p->data;
//Right son in the stack:
if(p->right!=nullptr){
s.push(p->right);
}
//Left son in the stack:
if(p->left!=nullptr){
s.push(p->left);
}
}
return;
}
/*Create binary tree*/
Node * createTree(char t[20],int *num){
char ch=t[(*num)];
(*num)++;
if(ch=='#'){
return nullptr;
}
//Create root node
Node *p=new Node();
p->data=ch;
//Create left subtree
p->left=createTree(t,num);
//Create right subtree
p->right=createTree(t,num);
return p;
}
int main()
{
char t[20]="AB#DF###CE###";
int i=0;//Counter
Node *root=nullptr;
root=createTree(t,&i);
nPreOrder(root);
return 0;
}
2. Middle root traversal
The steps are: ① traversing the left subtree, ② accessing the root, and ③ traversing the right subtree
Middle root traversal recursive algorithm
/*Middle root traversal*/
void inOrder(Node * root){
//Recursive exit
if(root==nullptr)
return;
//Traverse left subtree
inOrder(root->left);
//Access root
cout<<root->data;
//Traversing right subtree
inOrder(root->right);
}Middle root traversal non recursive algorithm
/*Middle root traversal non recursive algorithm*/
void nInOrder(Node * root){
if(root==nullptr){
return;
}
Stack s;
Node *p=root;
while( (!s.isEmpty()) || (p!=nullptr) ){
while(p!=nullptr){
s.push(p);
p=p->left;
}
p=s.pop();
cout<<p->data;
p=p->right;
}
}3. Back root traversal
The steps are: ① traverse the left subtree, ② traverse the right subtree, and ③ access the root
Back root traversal recursive algorithm
/*Back root traversal*/
void postOrder(Node * root){
//Recursive exit
if(root==nullptr)
return;
//Traverse left subtree
postOrder(root->left);
//Traversing right subtree
postOrder(root->right);
//Access root
cout<<root->data;
}Back root traversal non recursive algorithm
//Structure of stack 2 elements
struct NodeOfStack{
Node *pnode;
int times;//Stack times
NodeOfStack():pnode(nullptr),times(0){}
};
//Stack 2
class Stack2{
public:
Stack2():top(0){
for(int i=0;i<s_size;i++){
s[i].pnode=nullptr;
s[i].times=0;
}
}
//Push
void push(Node *p,int t){
if(top<s_size){
s[top].pnode=p;
s[top].times=t;
top++;
}else{
cout<<"Stack overflow!"<<endl;
return;
}
}
//Out of stack
NodeOfStack pop(){
if(top>0){
top--;
return s[top];
}
}
bool isEmpty(){
if(top==0)
return true;
else
return false;
}
private:
const int s_size=20;
NodeOfStack s[20];
int top;
};
/*Back root traversal non recursive algorithm*/
void nPostOrder(Node * root){
if(root==nullptr){
return;
}
Stack2 s;
s.push(root,0);
while(!s.isEmpty()){
NodeOfStack nos=s.pop();//The intermediate variable stores the data ejected from the stack every time
Node *p=nos.pnode;
if(nos.times==0){
s.push(nos.pnode,1);
if(p->left!=nullptr){
s.push(p->left,0);
}
}else if(nos.times==1){
s.push(nos.pnode,2);
if(p->right!=nullptr){
s.push(p->right,0);
}
}else if(nos.times==2){
cout<<p->data;
}
}
}4. Level traversal
Level traversal is to access all nodes of the binary tree from small to large according to the number of layers of the binary tree, and from left to right in the same layer
//queue
class Queue{
public:
Queue():font(-1),rear(0),q_count(0){
for(int i=0;i<q_size;i++){
q[i]=nullptr;
}
}
//Join the team
void qIn(Node *p){
if(q_count>=q_size){
//The queue is full
cout<<"Queue overflow!"<<endl;
return;
}
if(q_count==0){
//Queue is empty
font=rear;
}
q[rear]=p;
rear=(rear+1)%q_size;
q_count++;
}
//Out of the team
Node *qOut(){
if(q_count==0){
//Queue is empty
return nullptr;
}
Node *p=q[font];
font=(font+1)%q_size;
q_count--;
return p;
}
int q_count;//Number of elements in the queue
private:
const int q_size=20;//Queue size
Node *q[20];//q is logically a ring queue
int font;//The head of the queue is also the location of the element to be dequeued
int rear;//Where the next element joins the team
};
/*level traversal */
void levelOrder(Node * root){
if(root==nullptr){
return;
}
Queue q;
q.qIn(root);//Join the team
while(q.q_count>0){
Node *p=q.qOut();
cout<<p->data;
if(p->left!=nullptr){
q.qIn(p->left);
}
if(p->right!=nullptr){
q.qIn(p->right);
}
}
}(3) Creation of binary tree
As we said earlier, the creation of binary tree can be completed with the help of the idea of binary tree traversal algorithm. Now let's think about a question first - can a binary tree be uniquely determined only according to the first root sequence?
Obviously not. In order to solve this problem, we add some special symbols (such as' # ') in the first root sequence to represent the position of null pointer. For example, for the binary tree shown in the figure below, the first root sequence is ABDFCE, and the transformed sequence is ab#df####ce###

#include <iostream>
using namespace std;
struct Node{
Node *left;
Node *right;
char data;
Node():left(nullptr),right(nullptr),data('#'){}
};
/*Create binary tree*/
Node * createTree(char t[20],int *num){
char ch=t[(*num)];
(*num)++;
if(ch=='#'){
return nullptr;
}
//Create root node
Node *p=new Node();
p->data=ch;
//Create left subtree
p->left=createTree(t,num);
//Create right subtree
p->right=createTree(t,num);
return p;
}
int main()
{
char t[20]="AB#DF###CE###";
int i=0;//Counter
Node *root=nullptr;
root=createTree(t,&i);
return 0;
}expand
- According to the first root sequence and middle root sequence, a binary tree can be uniquely determined
- According to the posterior root sequence and middle root sequence, a binary tree can also be uniquely determined
- However, according to the first root sequence and the second root sequence, a binary tree cannot be uniquely determined