Data structure - binary tree - Application - BST & AVL & RBT
Binary sort tree (BST)
Basics
demand
Give you a sequence (7, 3, 10, 12, 5, 1, 9), which is required to query and add data efficiently.
-
Use array
(1) The array is not sorted. Advantages: it is added directly at the end of the array, which is fast. Disadvantages: the search speed is slow
(2) Array sorting, advantages: binary search can be used, which is fast. Disadvantages: in order to ensure the order of the array, when adding new data, after finding the insertion position, the following data needs to move as a whole, which is slow.
-
Use linked storage - linked list
No matter whether the linked list is orderly or not, the search speed is slow, the speed of adding data is faster than that of the array, and there is no need to move the data as a whole.
Solution - use binary sort tree
Introduction to binary sort tree

Binary sort tree is also known as binary search tree and binary search tree.
Binary sort tree is a good solution to the above problems. It has high performance in data query and addition. (of course, it refers to the average situation)
Binary sort tree code explanation
Full code (create tree, (middle order) traversal, add nodes, delete nodes, and other methods)
// Test code
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] arr = {7,3};
BinarySortTree binarySortTree = new BinarySortTree();
for (int i = 0;i < arr.length;i++){
binarySortTree.addNode(new Node(arr[i]));
}
System.out.println("Middle order traversal binary sort tree~");
binarySortTree.infixOrder();
System.out.println("*******");
// binarySortTree.deleteNode(2);
// binarySortTree.deleteNode(1);
// binarySortTree.deleteNode(1);
binarySortTree.deleteNode(7);
binarySortTree.infixOrder();
}
}
// BST
class BinarySortTree {
private Node root;
//Method of adding nodes
public void addNode(Node node){
if (root == null){
root = node;
} else {
root.addNode(node);
}
}
// Method of deleting node
public void deleteNode(int value){
if (root == null){
return;
} else {
Node targetNode = search(value);
// Can't find
if (targetNode == null){
return;
}
// If found, there is a special case: the whole number has only the target number
if (root.right == null && root.left == null){
root = null;
}
Node parent = searchParent(value);
// Deletion of leaf node
if (targetNode.left == null && targetNode.right == null){
if (parent.left != null && parent.left.value == value){
parent.left = null;
} else if (parent.right != null && parent.right.value == value){
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null){// Deletion of nodes with two child nodes
int replaceValue = delRightTreeMin(targetNode.right);
// int replaceValue = findMinNodeAndReturnValue(targetNode.right);
targetNode.value = replaceValue;
} else {// Deletion with one child node (left node or right node)
if (targetNode.left != null){// The child node is the left node
if (parent != null){
if (parent.left.value == value){// The point is the left node of its parent node
parent.left = targetNode.left;
} else { // The point is the right node of its parent node
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else {// The child node is the right node
if (parent != null){
if (parent.left.value == value){
parent.left = targetNode.right;
} else {
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
public void infixOrder(){
if (root == null){
System.out.println("The tree is empty and cannot be traversed");
} else {
root.infixOrder();
}
}
// Find the node to delete
private Node search(int value){
if (root == null){
return null;
} else {
return root.search(value);
}
}
// Find parent node
private Node searchParent(int value){
if (root == null){
return null;
} else {
return root.searchParent(value);
}
}
// Write a special method: used to delete nodes. The method is used to find and delete the smallest node of a subtree
// Note: the value of this node will also be returned.
/**
* @param node Incoming node (as the root node of binary sort tree)
* @return The value of the minimum node of the binary sort tree with node as the root node
*/
// The teacher's standard can be evaluated more. It's wonderful
private int delRightTreeMin(Node node){
Node target = node;
// Loop to find the left child node, and the minimum value will be found
while (target.left != null){
target = target.left;
}
// At this point, the target points to the smallest node
// Delete minimum node
deleteNode(target.value);
return target.value;
}
}
class Node {
public int value;
public Node left;
public Node right;
public Node(int value) {
this.value = value;
}
// Method of adding nodes
// Add nodes in the form of recursion. Pay attention to meeting the requirements of binary sort tree
public void addNode(Node node){
if (node == null){
return;
}
// Judge the value of the incoming node and the value relationship with the root node of the current subtree
if (node.value < this.value){
if (this.left == null){
this.left = node;
} else {
this.left.addNode(node);
}
} else {
if (this.right == null){
this.right = node;
} else {
this.right.addNode(node);
}
}
}
//Medium order traversal
public void infixOrder(){
if (this.left != null){
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null){
this.right.infixOrder();
}
}
// Find the node to delete
/**
* @param value The value of the node you want to delete
* @return If found, the node is returned; otherwise, null is returned
*/
public Node search(int value){
if (this.value == value){
return this;
} else if (this.value > value){
if (this.left == null){
return null;
}
return this.left.search(value);
} else {
if (this.right == null){
return null;
}
return this.right.search(value);
}
}
// Find the parent node of the node to delete
/**
* @param value The value of the node to find (find its parent node)
* @return The parent node of the node to be deleted is returned. If not, null is returned
*/
public Node searchParent(int value){
if ((this.left != null && this.left.value == value)
||
(this.right != null && this.right.value == value)){
return this;
} else if (this.value > value){
if (this.left == null){
return null;
}
return this.left.searchParent(value);
} else {
if (this.right == null){
return null;
}
return this.right.searchParent(value);
}
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
}
Detailed explanation of deletion function
In addition to deleting complex points, the functions of binary sort tree are very simple. Mainly analyze the implementation of deletion function.
There are three types of deleted nodes:
-
The node to be deleted is a leaf node (no subtree)
-
The node to be deleted has a child node (left child node or right child node)
-
The node to be deleted has two child nodes
The node to be deleted is a leaf node (no subtree)
In this case, you only need to find the node, then find the parent node of the node, and then delete the node directly with the parent node of the node.
The node to be deleted has a subtree (left subtree or right subtree)
In this case, you need to find the node first, and then find the parent node of the node. Then, you need to determine whether the node is the right or left subtree of the parent node. If it is the right subtree, after deleting the node, the original child node of the node needs to be connected to the right subtree of the parent node of the node. If it is the left subtree, Then the child nodes of the original node need to be connected to the left child tree of the parent node of the node.
The node to be deleted has two subtrees
In this case, there are two solutions. The video of Lao Han I learned here is about finding the right subtree node of the node. The method is to find the smallest node in the right subtree of the node to be deleted and delete this node (the code implementation needs to return this value), and assign the value of this node (the returned value) to the node to be deleted.
Imagine that the structure of this tree is the point to be deleted. The right subtree finds the smallest node. If the right subtree is not a single node, it must go to the left subtree, and then go through the cyclic or recursive search of the left subtree. After finding it, it is assigned to the value to be deleted, and the value to be deleted is equivalent to being deleted, Then the value assigned to the value to be deleted is actually equivalent. Therefore, in order to maintain the structure of the tree as a binary sort tree, because that number is the smallest value of the right subtree, it must be smaller than all the values of the right subtree, so the right subtree is larger than it. If it is placed on the node to be deleted, the right subtree is established first, Then it turns out to be a right subtree, so it must be larger than all the numbers of the left subtree of the node to be deleted, so the left subtree is smaller than it, and the left subtree is satisfied! In this way, the node is deleted, and the structure of binary sort tree is not destroyed.
Special case considerations - the root node has no parent node
Write the code according to the above three cases. The methods that can be extracted are: find and delete the node, find the parent node, find and delete the minimum value of a subtree whose node is the root node and return the value, and delete the main method.
However, when writing deletion methods, there will be a problem. Not every parent node has a parent node. For example, the root node has no parent node. Then, there are two cases of deleting the root node:
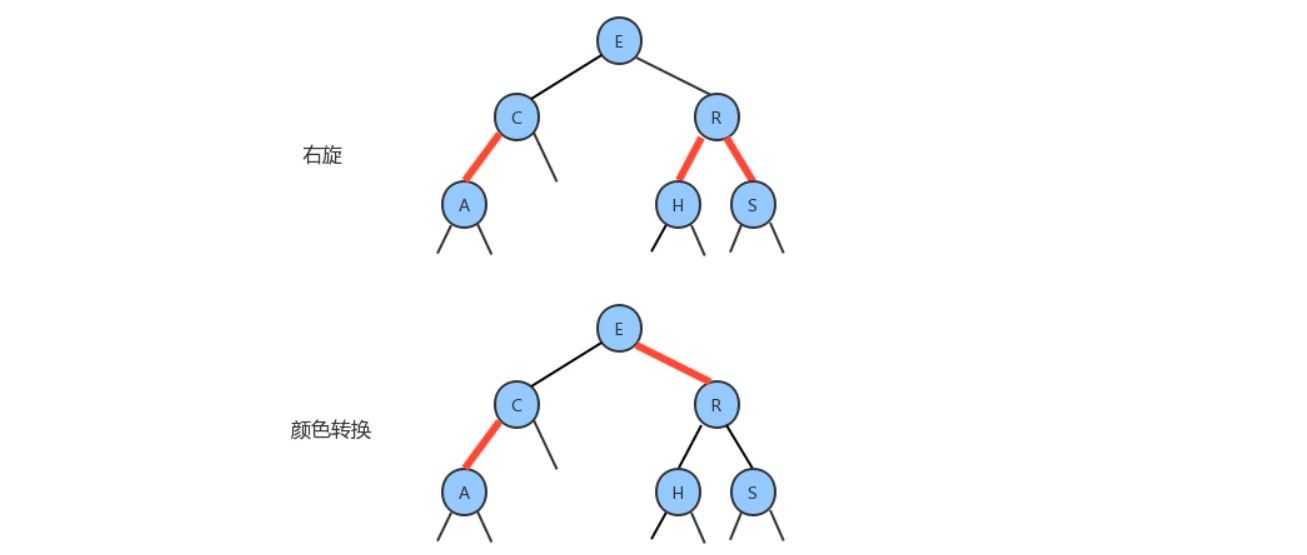
1. If the whole tree has only the target number, that is, the whole tree has only the root node, and the node needs to be deleted, you can directly assign null. (Figure 1 shows the solution code)
2. You need to delete root. Root has a left node or root has a right node. In this case, you need to judge whether the parent node exists before the judgment in the second case. If it does not exist, you need to delete the root node and enter the judgment domain in the second case. There must be a left or right node or subtree, so you need to connect the node directly to the root. (it is assigned to root) (in Figure 2, the red line is the code in this case)
3. In fact, the case of two nodes is automatically solved in the third case, so there is no need to change or add anything.
Figure 1:

Figure 2:

Balanced binary tree (AVL)
Basics
A case (requirement) for BST
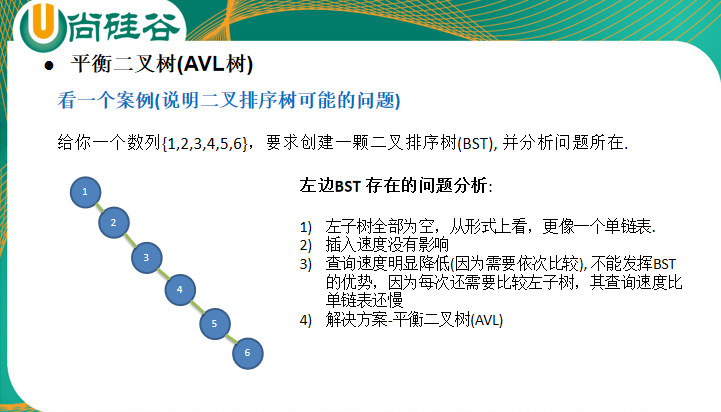
As shown in the figure above, the binary sort tree will have some extreme cases. In these cases, the query speed of the binary sort tree will be affected, and the simple improvement method is to balance the binary tree, which is improved on the basis of binary sort.
Introduction to binary balanced tree
- Balanced binary tree is also called self balancing binary search tree, also known as AVL tree, which can ensure high query efficiency.
- It has the following characteristics: it is an empty tree or the absolute value of the height difference between its left and right subtrees does not exceed 1, and both the left and right subtrees are a balanced binary tree. The common implementation methods of balanced binary tree include red black tree, AVL, scapegoat tree, tree, extension tree, etc. (Note: AVL above refers to the algorithm.)
Balanced binary tree code explanation
Full code of balanced binary tree (add balancing function based on the previous BST)
// Test code
public class AVLTreeDemo {
public static void main(String[] args) {
// int[] arr = {4,3,6,5,7,8};
// int[] arr = {10,12,8,9,7,6};
int[] arr = {10,11,7,6,8,9};
AVLTree avlTree = new AVLTree();
for (int i = 0;i < arr.length;i++){
avlTree.addNode(new Node(arr[i]));
}
avlTree.infixOrder();
System.out.println("Height after balance");
System.out.println(avlTree.getRoot().height());
System.out.println(avlTree.getRoot().leftHeight());
System.out.println(avlTree.getRoot().rightHeight());
System.out.println(avlTree.getRoot().left);
}
}
class AVLTree {
private Node root;
public Node getRoot() {
return root;
}
//Method of adding nodes
public void addNode(Node node){
if (root == null){
root = node;
} else {
root.addNode(node);
}
}
// Method of deleting node
public void deleteNode(int value){
if (root == null){
return;
} else {
Node targetNode = search(value);
// Can't find
if (targetNode == null){
return;
}
// If found, there is a special case: the whole number has only the target number
if (root.right == null && root.left == null){
root = null;
}
Node parent = searchParent(value);
// Deletion of leaf node
if (targetNode.left == null && targetNode.right == null){
if (parent.left != null && parent.left.value == value){
parent.left = null;
} else if (parent.right != null && parent.right.value == value){
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null){// Deletion of nodes with two child nodes
int replaceValue = delRightTreeMin(targetNode.right);
// int replaceValue = findMinNodeAndReturnValue(targetNode.right);
targetNode.value = replaceValue;
} else {// Deletion with one child node (left node or right node)
if (targetNode.left != null){// The child node is the left node
if (parent != null){
if (parent.left.value == value){// The point is the left node of its parent node
parent.left = targetNode.left;
} else { // The point is the right node of its parent node
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else {// The child node is the right node
if (parent != null){
if (parent.left.value == value){
parent.left = targetNode.right;
} else {
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
public void infixOrder(){
if (root == null){
System.out.println("The tree is empty and cannot be traversed");
} else {
root.infixOrder();
}
}
// Find the node to delete
private Node search(int value){
if (root == null){
return null;
} else {
return root.search(value);
}
}
// Find parent node
private Node searchParent(int value){
if (root == null){
return null;
} else {
return root.searchParent(value);
}
}
// Write a special method: used to delete nodes. The method is used to find and delete the smallest node of a subtree
// Note: the value of this node will also be returned.
/**
* @param node Incoming node (as the root node of binary sort tree)
* @return The value of the minimum node of the binary sort tree with node as the root node
*/
// The teacher's standard can be evaluated more. It's wonderful
private int delRightTreeMin(Node node){
Node target = node;
// Loop to find the left child node, and the minimum value will be found
while (target.left != null){
target = target.left;
}
// At this point, the target points to the smallest node
// Delete minimum node
deleteNode(target.value);
return target.value;
}
}
class Node {
public int value;
public Node left;
public Node right;
public Node(int value) {
this.value = value;
}
// Method for adding AVL tree:
// 1. Method of calculating left subtree
public int leftHeight(){
if (left == null){
return 0;
}
return left.height();
}
// 2. Method of calculating right subtree
public int rightHeight(){
if (right == null){
return 0;
}
return right.height();
}
// Basic method: calculate the height of the tree with the input node as the root node.
public int height(){
return Math.max(left == null ? 0 : left.height()
,right == null ? 0 : right.height()) + 1;
}
// Left rotation method
public void leftRotate(){
// First, you need to create a new node and assign the value of root to it
Node newNode = new Node(value);
// Then, you need to assign the left subtree (left node) of the root node to its left child node.
newNode.left = left;
// Then assign the left child node of the right child node of root to its right child node
newNode.right = right.left;
// Assign the right child node value (weight) of root to the root node
value = right.value;
// Point the right child node of root to the right child node of root's own right child node.
right = right.right;
// Finally, point the left child node of root to the new node created.
left = newNode;
}
// Right rotation method
public void rightRotate(){
Node newNode = new Node(value);
newNode.right = right;
newNode.left = left.right;
value = left.value;
left = left.left;
right = newNode;
}
// Method of adding nodes
// Add nodes in the form of recursion. Pay attention to meeting the requirements of binary sort tree
public void addNode(Node node){
if (node == null){
return;
}
// Judge the value of the incoming node and the value relationship with the root node of the current subtree
if (node.value < this.value){
if (this.left == null){
this.left = node;
} else {
this.left.addNode(node);
}
} else {
if (this.right == null){
this.right = node;
} else {
this.right.addNode(node);
}
}
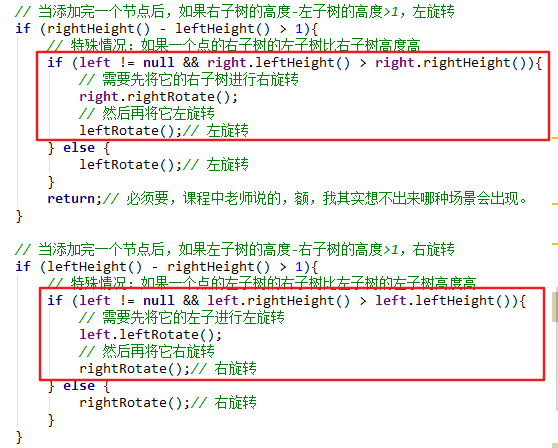
// After adding a node, if the height of the right subtree - the height of the left subtree is > 1, rotate left
if (rightHeight() - leftHeight() > 1){
// Special case: if the left subtree of the right subtree of a point is higher than the right subtree
if (left != null && right.leftHeight() > right.rightHeight()){
// You need to rotate its right subtree to the right first
right.rightRotate();
// Then rotate it to the left
leftRotate();// Left rotation
} else {
leftRotate();// Left rotation
}
return;// Yes, as the teacher said in the course, well, I can't think of any scene.
}
// After adding a node, if the height of the left subtree - the height of the right subtree is > 1, rotate the right
if (leftHeight() - rightHeight() > 1){
// Special case: if the right subtree of the left subtree of a point is higher than the left subtree of the left subtree
if (left != null && left.rightHeight() > left.leftHeight()){
// You need to rotate its left child first
left.leftRotate();
// Then rotate it to the right
rightRotate();// Right rotation
} else {
rightRotate();// Right rotation
}
}
}
//Medium order traversal
public void infixOrder(){
if (this.left != null){
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null){
this.right.infixOrder();
}
}
// Find the node to delete
/**
* @param value The value of the node you want to delete
* @return If found, the node is returned; otherwise, null is returned
*/
public Node search(int value){
if (this.value == value){
return this;
} else if (this.value > value){
if (this.left == null){
return null;
}
return this.left.search(value);
} else {
if (this.right == null){
return null;
}
return this.right.search(value);
}
}
// Find the parent node of the node to delete
/**
* @param value The value of the node to find (find its parent node)
* @return The parent node of the node to be deleted is returned. If not, null is returned
*/
public Node searchParent(int value){
if ((this.left != null && this.left.value == value)
||
(this.right != null && this.right.value == value)){
return this;
} else if (this.value > value){
if (this.left == null){
return null;
}
return this.left.searchParent(value);
} else {
if (this.right == null){
return null;
}
return this.right.searchParent(value);
}
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
}
Add method to supplement detailed explanation of balance process
The difference between balanced binary tree and binary sort tree is that when adding and deleting nodes (the same idea is omitted here) the balanced binary tree will automatically balance the tree and keep the tree as an AVL tree structure. In this way, the efficiency of query is guaranteed in all cases.
Simply put, after adding nodes, you need to judge the height of the left and right subtrees, and then there are several cases
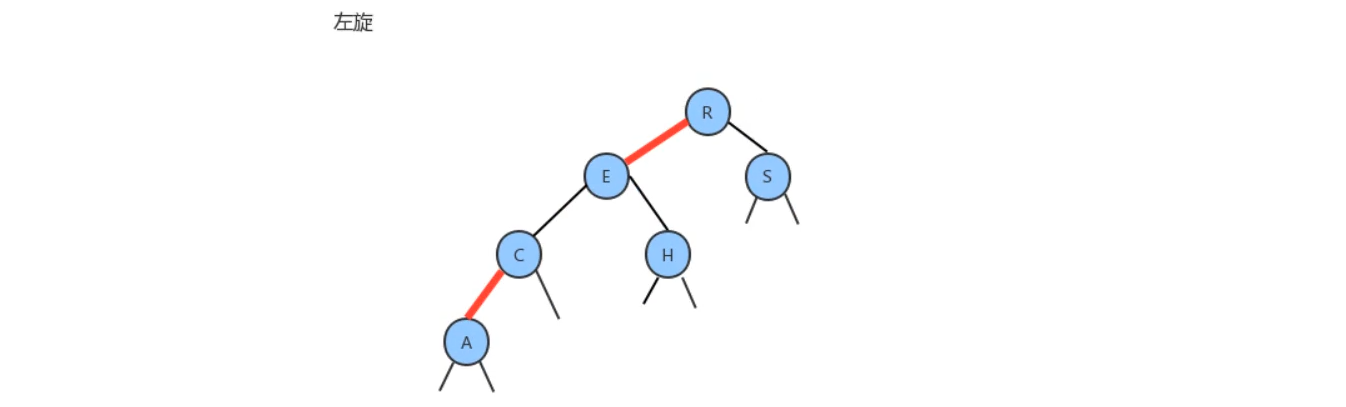
The first is as follows: (in this case, the right subtree is higher than the left subtree, and the right subtree of the right subtree is higher than the left subtree.)

Idea: rotate left
As the name suggests, it looks like a left rotation. In principle, it can be seen directly.
First, you need to create a node whose value is the value of the root node of the tree, and then point the left child node of the node to the left child node of the root node. The idea is that the node will later be the left node of the root node, because the value of the created new node is the same as that of the root node, Therefore, its left node points to the left node of the original root node, which will not affect the structure.
Then, you need to point the right child node of the newly created node to the left child node of the right node of the root node, because the left child node of the right child node of the root node must be larger than the root node, so it is larger than the newly created node, so the node placed on the right child node of the newly created node will not destroy the structure of the tree.
Next, it is very important to assign the value of the right child node of the root node to the root node. In this step, because the value of the original root node is the same as that of the newly created node, and the right child node of the original root node must be larger than the root node, the root node must be larger than the newly created node after the assignment, which meets the requirements of placing the newly created node on the left child node of the root node, Then we need to elaborate. In the previous step, the reason why the right node of the newly created node points to the left child node of the right child node of the root node is that it will not destroy the structure. It is said that it is established as the right node of the newly created node, and at the same time, because it is originally the left child node of the right child node of the root node, Then it and its node must be smaller than the right child node of the root node. Then the value of the assigned root node is the same as that of the right child node of the root node, which is greater than it. Therefore, the whole newly created node is actually smaller than the root node. This is also the reason why it is established to point the left child node of the root node to the newly created node.
Next, point the right child node pointer of the root node to the right child node of the right child node. Firstly, this will not change the structure, and then this step is equivalent to deleting the right child node of the original root node. Because the right child node pointer of the root node no longer points to it, it will become garbage and will be garbage collected. Then, point the pointer of the left child node of the root node to the newly created node. This process is shown on the right of the above figure. Finally, a balanced tree is formed. The whole process is actually moving the value of the right child tree to the left child tree. The reason for this is the analysis of the previous process to ensure that it conforms to the rules of binary sort tree.
The second case: (in this case, the left subtree is higher than the right subtree, and the left subtree of the left subtree is higher than the right subtree.)

Idea: rotate left
Like the left rotation idea, it's just symmetrical. Slightly.
Case 3 / 4:
The right subtree is taller than the left subtree, but the right subtree of the right subtree is shorter than the left subtree of the right subtree.
The left subtree is taller than the right subtree, but the left subtree of the left subtree is shorter than the right subtree of the left subtree.
With a single rotation, it will look like this:

Solution: double rotation
The latter two cases are actually special cases. If single rotation is used in these two cases, the rotation still does not meet the rules of balanced binary tree (the height difference between the two subtrees exceeds 1), so a new solution is needed.
In class, Lao Han explained the method of double rotation. In short, it is to use left and right rotation once respectively. If the right subtree is higher than the left subtree, but the right subtree of the right subtree is lower than the left subtree of the right subtree, you need to rotate the right subtree first, which will make the height of the right subtree of the right subtree higher than the left subtree of the right subtree. In this way, the first case is satisfied, and then rotate the node left again. In the other case, the rotation is just the opposite.
Summary:
The right subtree is taller than the left subtree, but the right subtree of the right subtree is shorter than the left subtree of the right subtree. – > Rotate the right subtree right and then left
The left subtree is taller than the right subtree, but the left subtree of the left subtree is shorter than the right subtree of the left subtree. – > Rotate left subtree first and then right
As shown in the following figure, the red box part can be completed. (code above the screenshot)
Red black tree (RBT)
Basics
definition
Lao Han's course has been out for a long time. In the previous course, I didn't talk about the red and black tree. Here I see the red and black tree of the black horse.
The first is the definition. What I understand is that the red black tree simulates the 2-3 tree structure with a binary sort tree and is completed through the concept of red black link. Therefore, before learning the red black tree, you need to learn the basic concept of 2-3 tree.
A detailed cut of a dark horse:
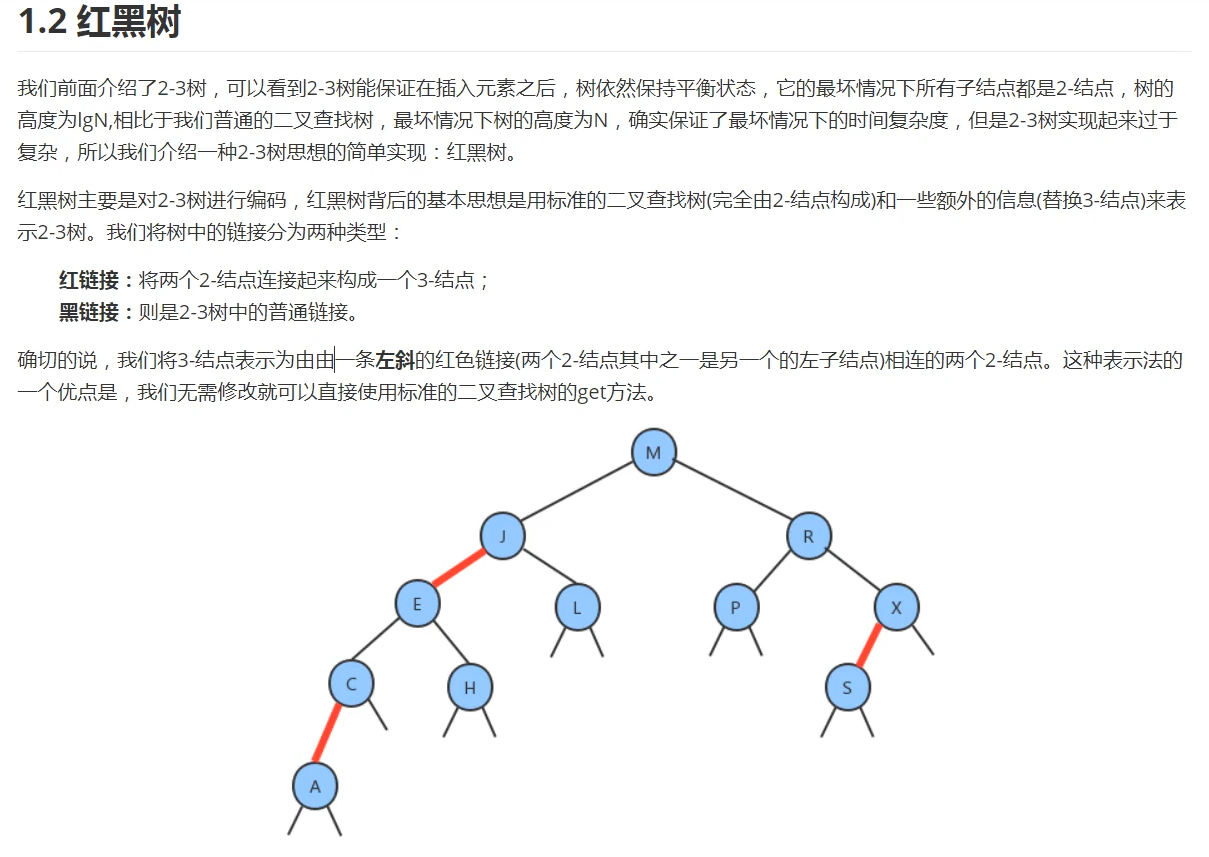
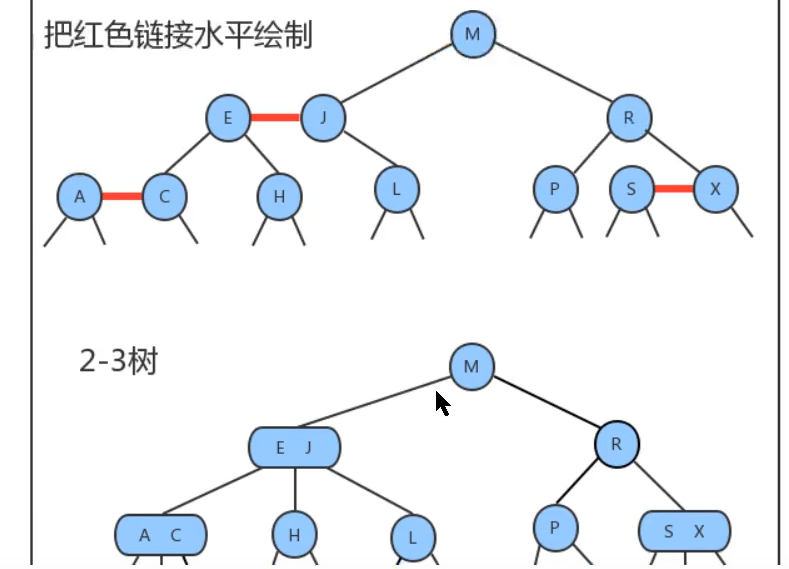
As shown in the figure above, because the 2-3 tree is simulated, the height problem of this binary sort tree can also be solved, but it is not "completely balanced" like AVL tree.
Note: the red black tree can also be a simulated 2-3-4 tree. It is a common red black tree in the introduction to the algorithm. Its principle is not much different, so it is omitted.
Comparison between red black tree and balanced binary tree
The following figure summarizes well: the original link https://www.jianshu.com/p/37436ed14cc6

Detailed explanation of red black tree code
Red black tree full code (2-3 tree version)
package redblacktree;
public class RedBlackTree<Key extends Comparable<Key>,Value> {
// Root node
private Node root;
// Record the number of elements in the tree
private int N;
// Red link
private static final boolean RED = true;
// Black link
private static final boolean BLACK = false;
// Node class
private class Node{
// Storage key
public Key key;
// Stored value
private Value value;
// Record left child node
public Node left;
// Record right child node
public Node right;
// The color of the link that its parent node points to
public boolean color;
public Node(Key key, Value value, Node left, Node right, boolean color) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
this.color = color;
}
// Write a middle order traversal to see the structure of the red and black tree
public void infixOrder(Node x){
if (x.left != null){
infixOrder(x.left);
}
System.out.println(x.key);
if (x.right != null){
infixOrder(x.right);
}
}
}
// Gets the number of elements in the tree
public int size(){
return N;
}
// Judge whether the parent pointing link of the current node is red
private boolean isRed(Node x){
if (x == null){
return false;
}
return x.color == RED;
}
/**
* Left rotation
* @param h
* @return
*/
private Node rotateLeft(Node h){
// Get the right child node of node h, point to it with the x pointer, and determine its address
Node x = h.right;
// Point the right pointer of h to the left child node of x
h.right = x.left;
// Point the left pointer of x to the h node
x.left = h;
// Make the color attribute of x equal to the color attribute of h
x.color = h.color;
// Set the color attribute of h to RED
h.color = RED;
return x;
}
/**
* Right rotation
* @param h
* @return
*/
private Node rotateRight(Node h){
// Get the left child node of node h, point to it with the x pointer, and determine its address
Node x = h.left;
// Point the left pointer of h to the right child node of x
h.left = x.right;
// Point the right pointer of x to the h node
x.right = h;
// Make the color attribute of x equal to the color attribute of h
x.color = h.color;
// Set the color attribute of h to RED
h.color = RED;
return x;
}
/**
* Color reversal is equivalent to splitting 4- nodes
* @param h
*/
private void flipColors(Node h){
// The current node turns red
h.color = RED;
// The left and right child nodes turn black
h.left.color = BLACK;
h.right.color = BLACK;
}
/**
* Complete the insert operation on the entire tree
* @param key
* @param val
*/
public void put(Key key,Value val){
root = put(root,key,val);
// The color of the root node is always black.
root.color = BLACK;
}
/**
* In the specified tree, complete the insertion operation and return to the new tree after adding elements
* @param h
* @param key
* @param val
*/
private Node put(Node h,Key key,Value val){
// Judge h. if h is null, it is the end. Directly encapsulate the data as a node and then return.
if (h == null){
// Quantity + 1
N++;
return new Node(key,val,null,null,RED);
}
// If h is not empty, you need to compare the key and key size of the H node
int cmp = key.compareTo(h.key);
if (cmp < 0){
// If the comparison result is less than the key value of h, continue to search and insert to the left
// Note: the assignment to h.left is because flipping may occur.
h.left = put(h.left,key,val);
} else if (cmp > 0){
// If the comparison result is greater than the key value of h, continue to search and insert to the right
h.right = put(h.right,key,val);
} else {
// The key value equal to h needs to be replaced
h.value = val;
}
// Left rotation: when the left child node of the current node h is black and the right child node is red, left rotation is required
if (isRed(h.right) && !isRed(h.left)){
h = rotateLeft(h);
}
// Rotate right: when the left child node of the current node h and the left child node of the left child node are red, rotate right
if (isRed(h.left) && isRed(h.left.left)){
h = rotateRight(h);
}
// Color reversal: when the left and right child nodes of the current node are red, color reversal is required
if (isRed(h.left) && isRed(h.right)){
flipColors(h);
}
return h;
}
// Find the corresponding value from the tree according to the key
public Value get(Key key){
return get(root,key);
}
// From the specified tree x, find the value corresponding to the key
private Value get(Node x,Key key){
if (x == null){
return null;
}
// Compare the key and key size of x node
int cmp = key.compareTo(x.key);
if (cmp < 0){
return get(x.left,key);
} else if (cmp > 0){
return get(x.right,key);
} else {
return x.value;
}
}
// Use to view the structure of red and black trees
public void infixOrder(){
root.infixOrder(root);
}
}
Test code:
package redblacktree;
public class RedBlackTreeTest {
public static void main(String[] args) {
// Create red black tree
RedBlackTree<Integer,String> tree = new RedBlackTree<>();
// Insert an element into the tree
tree.put(1,"Zhang San");
tree.put(2,"Li Si");
tree.put(3,"Wang Wu");
tree.put(4,"have a look");
// Get elements from tree
// String r1 = tree.get(1);
// System.out.println(r1);
//
// String r2 = tree.get(2);
// System.out.println(r2);
//
// String r3 = tree.get(3);
// System.out.println(r3);
//
// String r4 = tree.get(4);
// System.out.println(r4);
tree.infixOrder();
}
}
Detailed explanation of red black tree - node insertion of red black tree
The difficulty of red black tree mainly lies in inserting nodes. Firstly, inserting nodes needs to be divided into four cases:
- Insert a new key into a single 2- node
- Insert a new key to the 2-node at the bottom
- Inserts a new key into a double key tree
- Insert a new key to the 3-node at the bottom of the tree
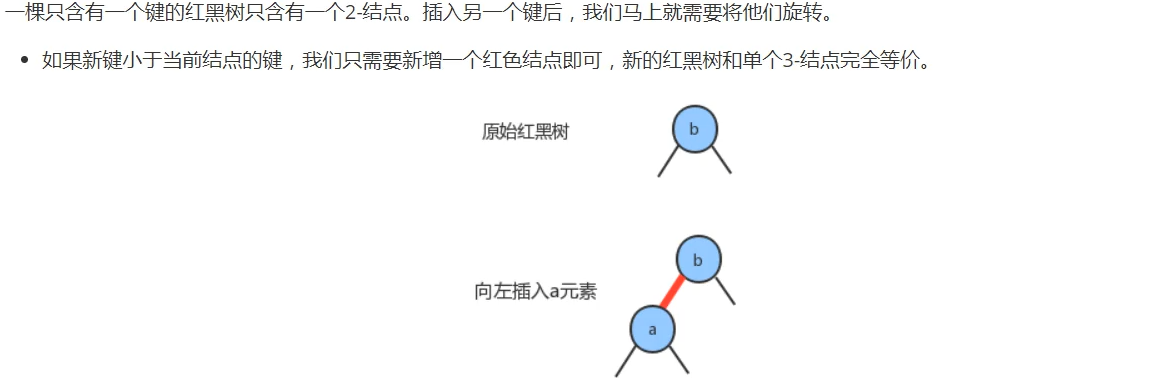
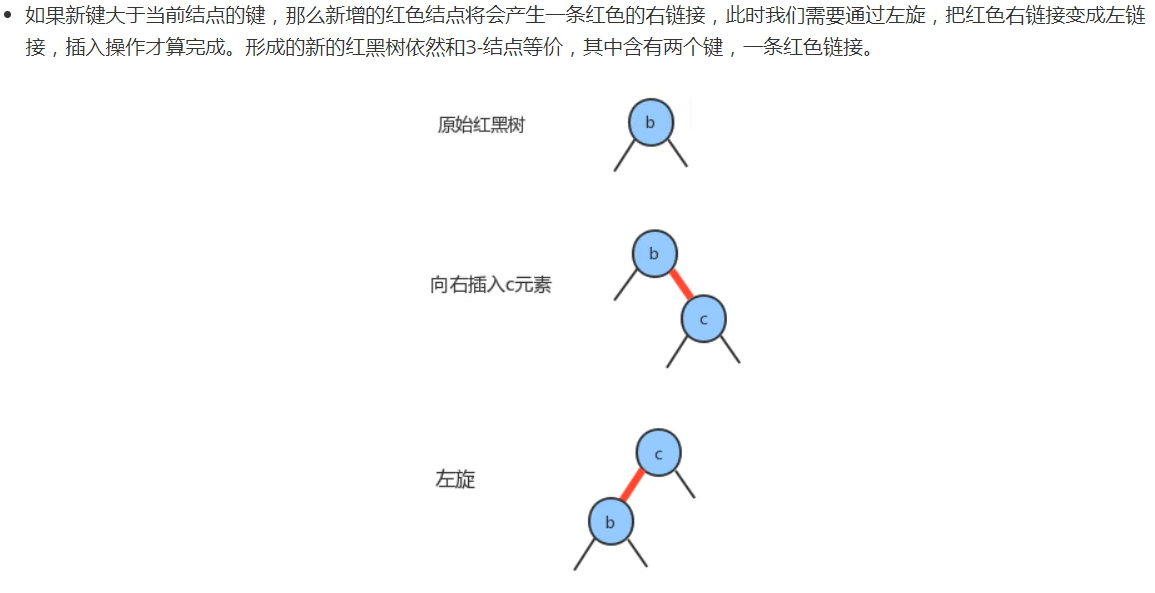
Insert a new key into a single 2- node
Two cases: as shown below:
Supplement: about rotation
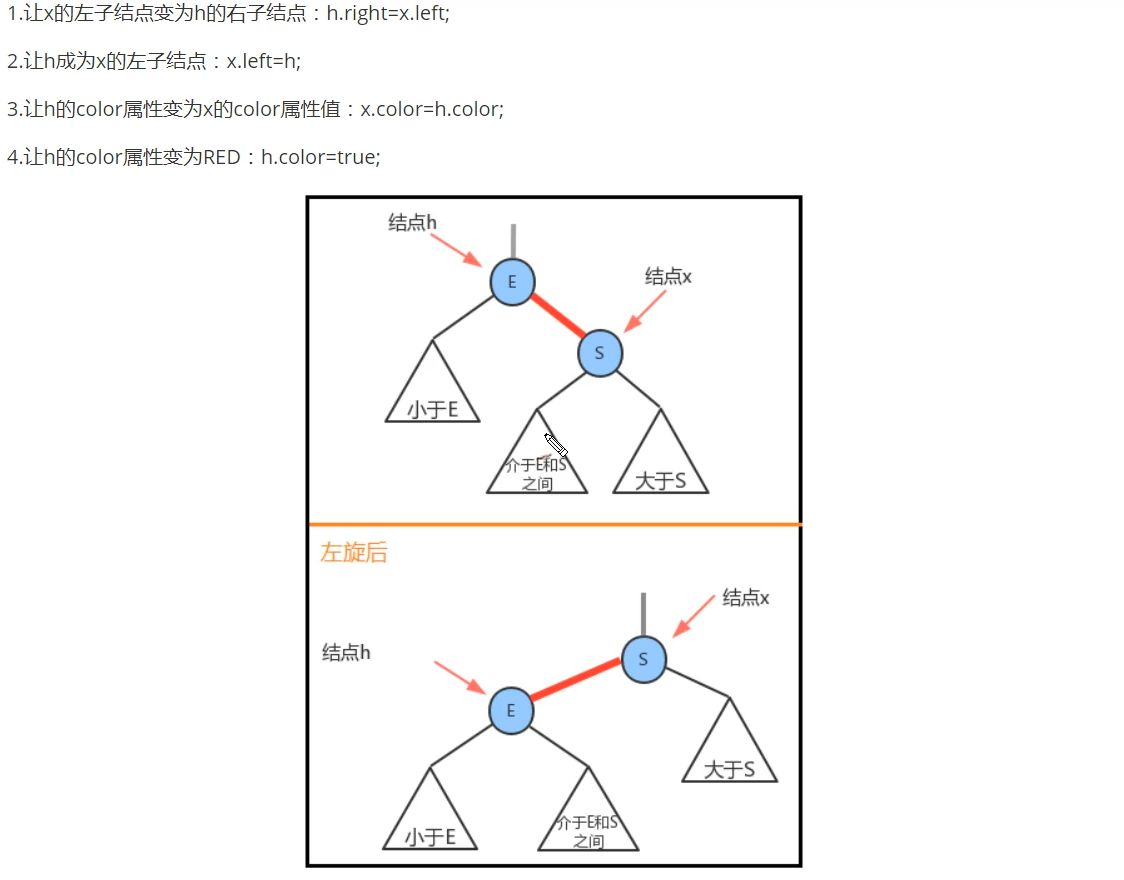
The rotation method of dark horse is somewhat different from that of old Han in Silicon Valley. Old Han's method is described in the avl tree above, which uses a new node to assist the connection, The method of dark horse video is more concise (but I'm not sure, because I know Lao Han's method first and understand it almost). I don't use a new node, but I need to return to the root node of the rotated subtree and reconnect with the position of the original parent node to wake up.
A screenshot for easy understanding: (right-handed analogy)
Insert a new key to the 2-node at the bottom
Insert the same as above into the 2-node at the bottom. If it is less than direct insertion, if it is greater than left rotation after insertion.

Insert a new key into a double key tree (3-node)
There are three ways to insert a new key into a double key tree:
The first case:

The above figure shows the first case. After the new key is inserted, b the two links (pointers) pointing to the left and right child nodes are red, which does not comply with the red black tree rules and requires color reversal. Color reversal is supplemented below.
Note: the second tree form in this process is actually the temporary 4-node in the process of inserting nodes in the 2-3 tree.
Color reversal:
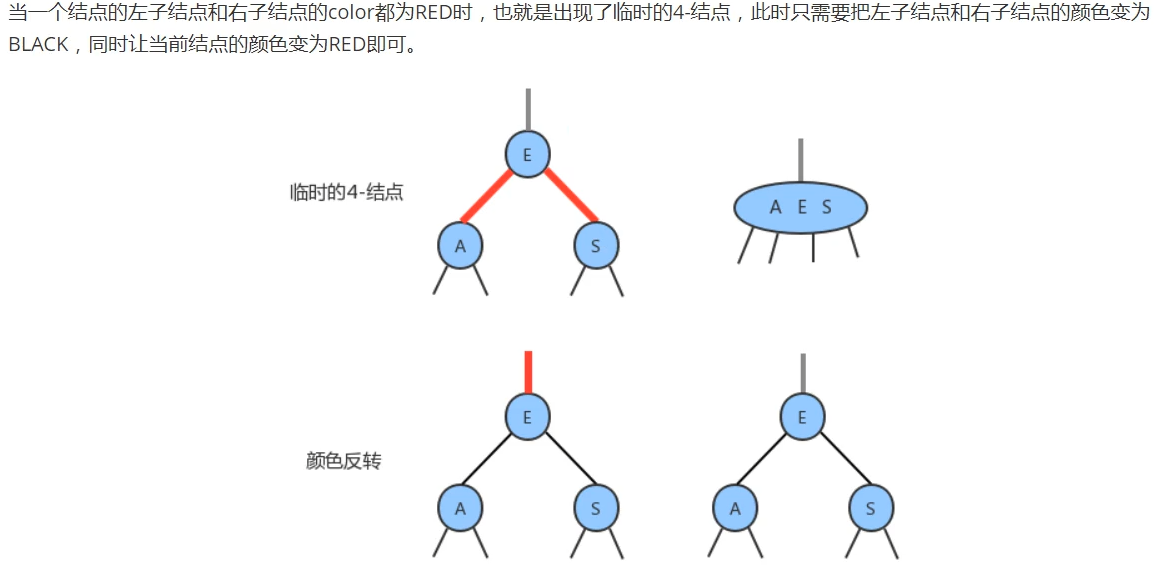
As shown in the figure above, the parent link of the root node of the subtree changes to red after the color is reversed. Note: therefore, the color of the parent link of the node is the attribute of the node.
Then, we need to add that the color of the root node is always black because the root node has no parent node. At the same time, when implementing the code, it should also be noted that the color of the root node needs to be set to black after each insertion operation (because the node to which the root node pointer needs to point may change after insertion and rotation).
The second case:
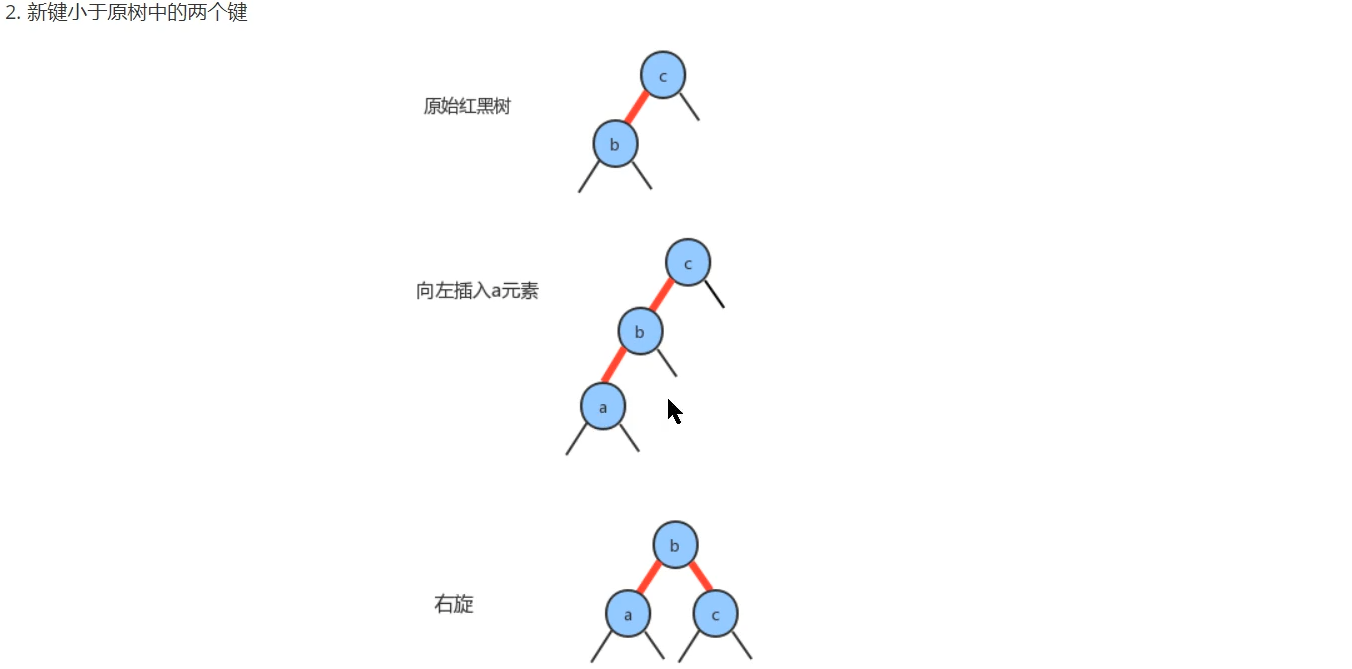

The third case:

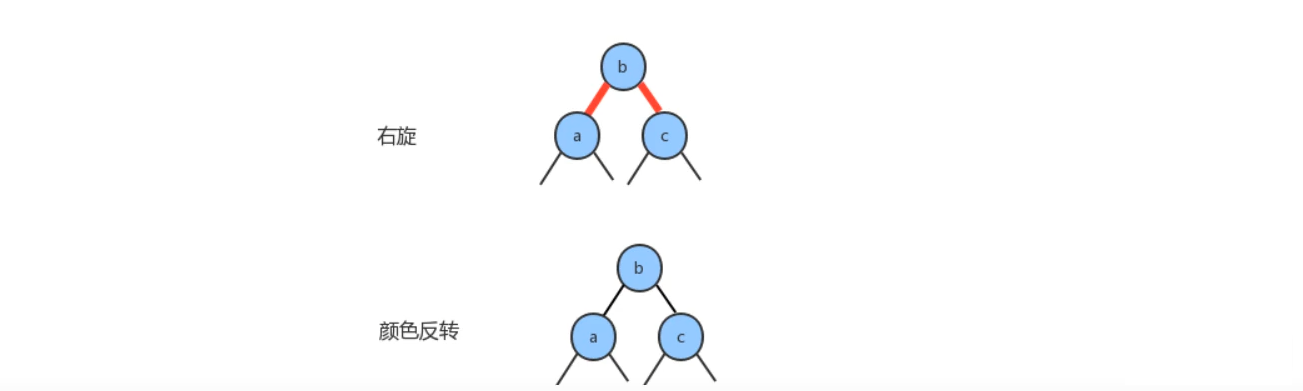
Insert a new key to the 3-node at the bottom of the tree