Binary Tree

The feature of a binary tree is that if the current node is larger than the root node, it is placed on the right side of the root node, otherwise it is placed on the left side.

Create Binary Tree Node

         function Node(element, left, right) {
            this.element = element;
            this.left = left;
            this.right = right;
            this.show = function () {
                return this.element;
            };
        }

          function BST() {
            this.root = null;
            }

1. Insert data

The data insertion of binary trees is a bit complex compared to each other, and there are many conditions to judge, which need to be analyzed one by one:

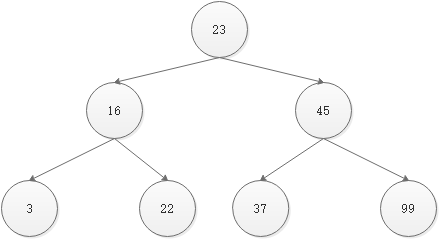
If you insert a piece of data: 23,45,16,37,3,99,22

After insertion, it should be shown as follows:

           this.insert = function (element) {
            //1, create a new node
            var node = new Node(element, null, null,null);
            if (this.root == null) {
                this.root = node;
            } else {
                //Set Parent Node
                var parent = this.root;
                while (true) {
                    var buffer = parent;
                    if (node.element > parent.element) {
                        //Compare with the right node of the root node
                        parent = parent.right;
                        if (parent == null) {
                            node.parent = buffer;
                            buffer.right = node;
                            break;
                        }
                    } else {
                        //Compare with the left node of the root node
                        parent = parent.left;
                        if (parent == null) {
                            node.parent = buffer;
                            buffer.left = node;
                            break;
                        }

                    }
                }
            }
        }

2. Find Nodes, Maximum, Minimum

Find the maximum and minimum value, according to the characteristics of binary tree insertion data, find the minimum value only needs to keep looking for the left node until the left node is empty, the maximum value is the same

         //Find Node
        this.find = function (element) {
            var node = this.root;
            while (true) {
                if (node == null)
                    return node;
                if (node.element == element) {
                    return node;
                } else if (element < node.element) {
                    node = node.left;
                } else if (element > node.element) {
                    node = node.right;
                }
            }
        }

        // Find Minimum
        this.getMin = function (element) {
            var node = this.find(element);
            // console.log(node);
            while (node.left != null) {
                node = node.left;
            }
            return node;
        }

        // Find Maximum
        this.getMax=function (element) {
            //Find the current node
            var node=this.find(element);
            while(node.right!=null){
                node=node.right;
            }
            return node;
        }

3. Delete Nodes

The principle of deleting a node in a binary tree is to delete the current node, move the right node of the current node to the position of the current node, and move the left node of the current node to the smallest node of the right node.

If node 45 is deleted: since the right node of 45 is 99 and 99 has no left node, then 37 nodes are added to the left node of 99;

Delete 16:

Delete Root Node 23: 45 becomes the root node after deleting the root node, 23 becomes the left node of 45 left node

The code is as follows:

         //Delete Node
         this.remove = function (element) {
            //Get Current Node
            var node = this.find(element);
            if (node == null)
                return;
            // Determine if the current node is the root node
            if (node.parent == null) {
                //If the root node, find the right node of the root node
                if (node.right != null) {
                    this.root = node.right;
                    this.root.parent = null;
                    //Get the smallest node of the right node of the root node
                    var minNode = this.getMin(node.right.element);
                    minNode.left = node.left;
                    node.left.parent=minNode;
                } else {
                    this.root = node.left;
                    this.root.parent = null;
                }

            }else{
                //If it is not the root node, it is consistent with the algorithm of the root node
                // Find the parent of the current node                
                var parent = node.parent;
                //Determines whether the current node is the right or left node of the parent node
                // Right node if current node value is greater than parent node
                if(node.element>parent.element){

                    if(node.right!=null){
                        var minNode = this.getMin(node.right.element);
                        minNode.left=node.left;
                        node.left.parent=minNode;
                        parent.right=node.right;
                        node.right.parent=parent;
                    }else{
                        parent.right=node.left;

                        if(node.left!=null)
                            node.left.parent=parent;
                    }

                }else{
                    // Left node if current node value is greater than parent node
                    if(node.right!=null){
                        var minNode = this.getMin(node.right.element);
                        minNode.left=node.left;
                        node.left.parent=minNode;

                        parent.left=node.right;
                        node.right.parent=parent;
                    }else{
                        parent.left=node.left;
                        if(node.left!=null)
                            node.left.parent=parent;
                    }
                }
            }
        }