Data structure (I) school online link.
Under data structure (school online).
Station B link.
Method steps:
1. Watch the video of station B, type the code and take notes. Online segmentation according to school
2. Compare whether the online video of the school is missing.
3. Do school online exercises and supplement notes.
Chapter - Introduction
calculation
Object: rules and skills
Objective: high efficiency and low consumption
Computers: tools and means
Calculation is the goal
Rope computer and its algorithm
- Input: any given line l and its upper point A
- Output: A vertical line passing through l made by A
Algorithm (ancient Egypt):
1. Take 12 equal length ropes and connect them into a ring
2. From point A, straighten 4 sections of rope along l and fix it to point B
3. Find the end point C of the third rope in the other direction
4. Move point C and straighten the remaining 3 + 5 ropes.
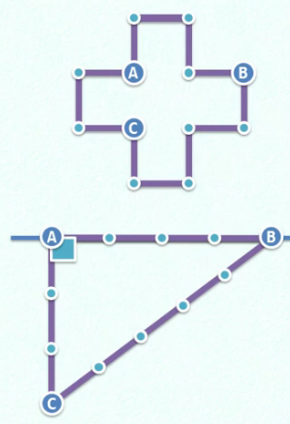
- By Pythagorean theorem: the length ratio of three sides is 3:4:5, which must form a right triangle
- Fix point B first (the straight line is known and easy to determine). Then there is point C (note that one side has 3 segments and one side has 5 segments, which is fixed, so point C can also be determined)
Repeat the process mechanically
Ruler and gauge computer and its algorithm
- Give any line segment AB on the plane (input) and divide it into three equal parts (output)
Algorithm:
1. A ray that does not coincide with AB is emitted from a ρ
2. In ρ Take AC '= C'd' = D 'B`
3. Connection B 'B
4. Make parallel lines of B through d 'and intersect AB at D
5. Make a parallel line of B 'B through C', and intersect AB at C
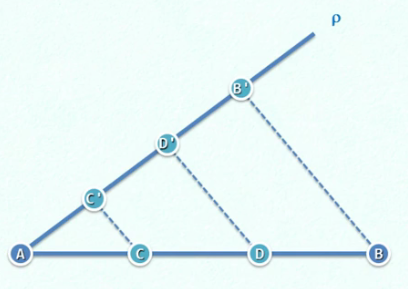
- Similar triangle theorem
It is decomposed into several steps and executed mechanically.
P4
Calculation = information processing
With the help of a certain tool, in accordance with certain rules, in a clear and mechanical form.
Algorithm: a sequence of instructions designed to solve a specific problem under a specific computing model.
Input, output, correctness, certainty, feasibility, finiteness.
P5
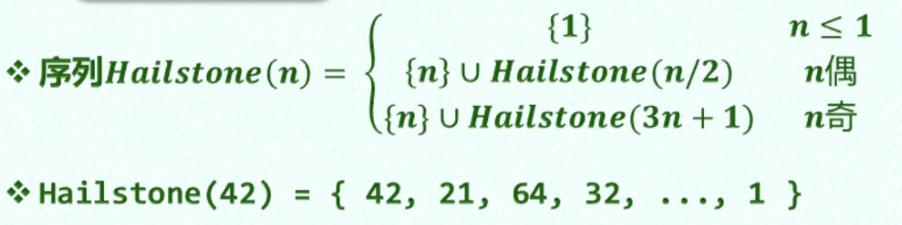
- Occasionally rise, overall decline
int halistone(int n) {// Calculate the length of the sequence Hailstone(n)
int length = 1;
while (n > 1) {
(n % 2) ? n = 3 * n + 1 : n /= 2; length++;
}
return length;
}
- The length is not proportional to n
Some n results are infinite. Whether it is an algorithm is controversial
- Program ≠ algorithm
- Dead loop or stack overflow
P6 good algorithm
Efficiency: as fast as possible; The storage space shall be as small as possible.
P7
Data Structure + Algorithm (DSA)
measure
To measure is to know.
If you can not measure it,
you can not improve it.
— Lord Kelvin
P8
Cost: time + storage space
scale
P9
P10
P11
Turing machine (TM)
- Tape is evenly divided into cells in turn, each marked with a certain character, and the default is' # '
- Head: always aim at a cell and can read and rewrite characters in it. After each beat, you can turn to the adjacent grid on the left or right.
- State: TM (Turing machine) is always in one of the limited states. After each beat, it can turn to another state (according to the rules).
- Transition Function: (q, c; d, L/R,p): if the current status is q and the current character is c, rewrite the current character to d; Turn to the adjacent grid on the left / right; Enter p status. Once it turns into a specific state 'h', it stops.
P12 ？
TM : Increase
Function: add one to binary non negative integer
P13 RAM(Random Access Machine)
1. There is no limit on the total number of registers.
2. Each basic operation requires only constant time
P14 RAM instance?
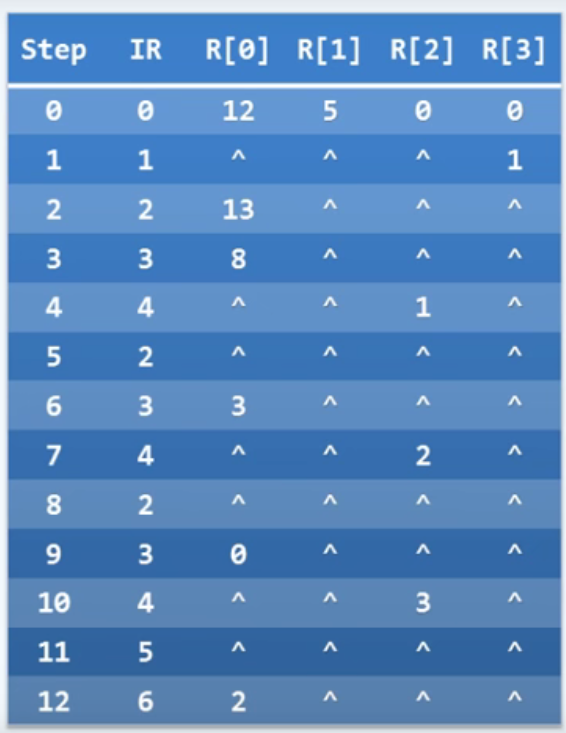
Conclusion:
- The execution process can be recorded as a table
- The number of rows in the table is the total number of basic instructions executed
P15
Mathematic is more in need of good notations than of new theorems.
----Alan Turing
Good sign > New Theory
A good book seeks no understanding
Every time you know something, you will gladly forget to eat
----Tao Yuanming
- Potential to solve large-scale problems (long term)
- Focus on key aspects (mainstream)
For scale n input
1. Basic operands to perform: T(n)
2. Number of storage units to be occupied: S(n) (usually not considered)
P16
enlarge
Upper bound:
Lower bound (the best case of the algorithm)
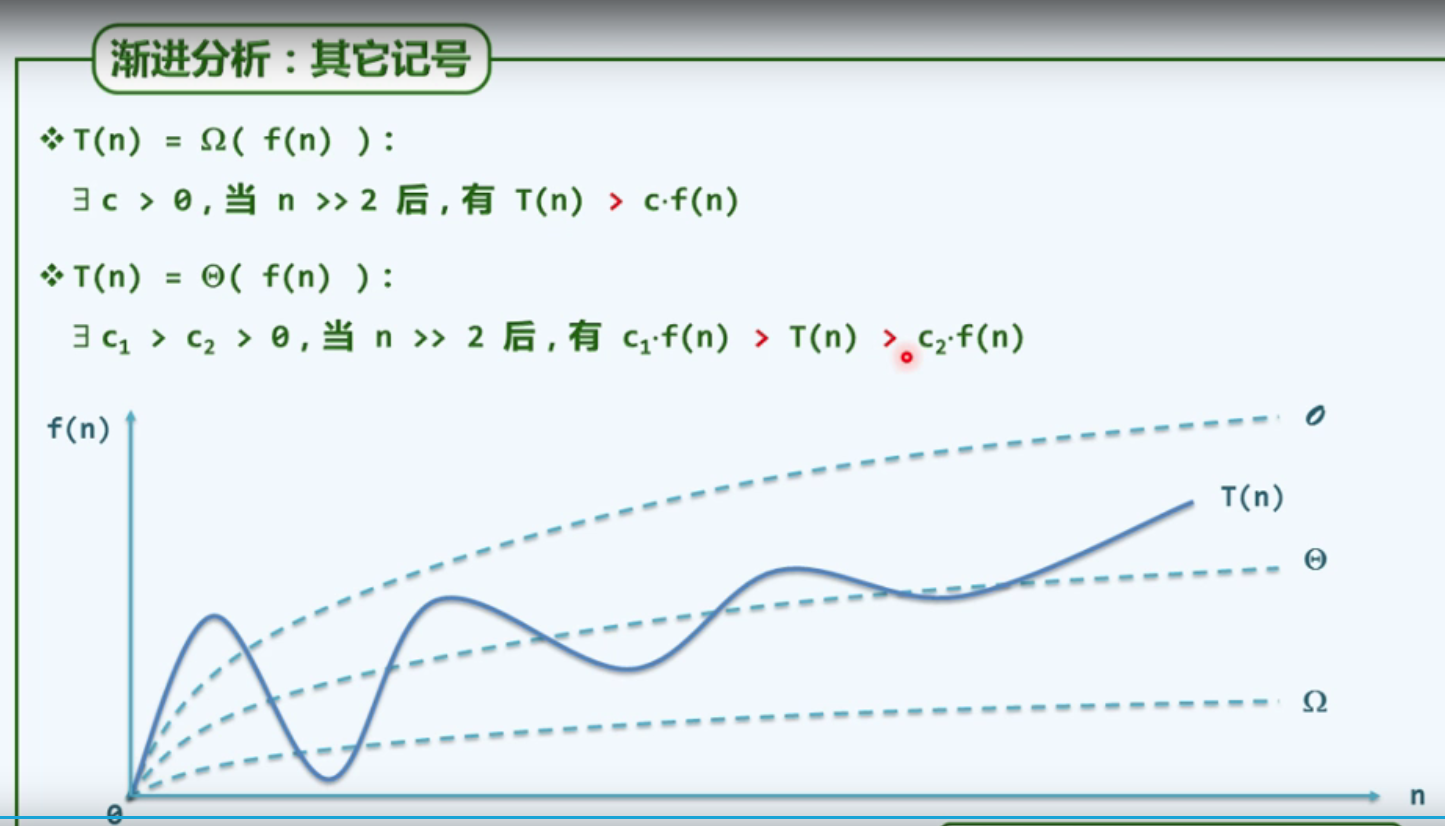
P17
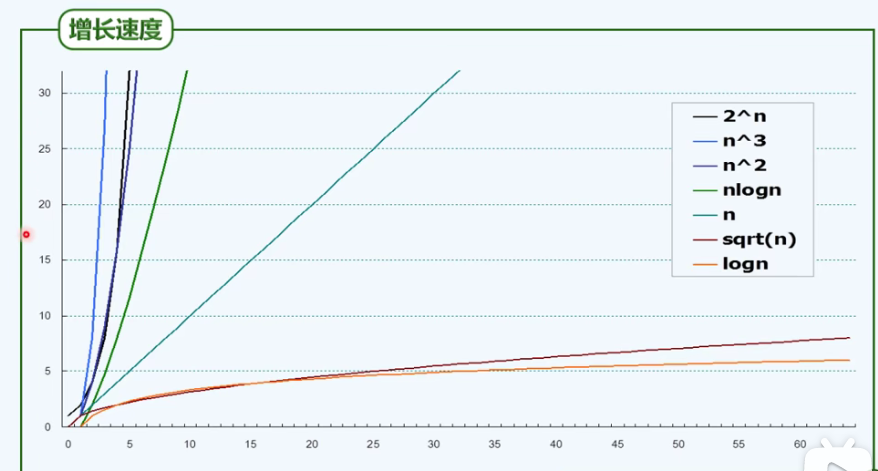
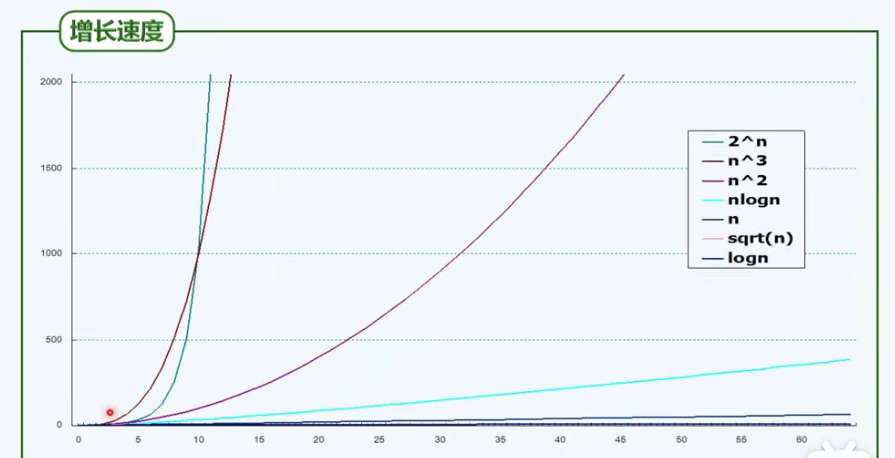
1. O(1): without steering (loop, call, recursion, etc.), it must be executed in sequence
2. O(logn) is very effective, and the complexity is infinitely close to a constant
3,O(n^c)
4. Linear O(n)
5. T(n) = a^n, intolerable
P20
Example: 2-Subset
S contains n positive integers and the sum is 2m
Whether S has subset T, and its sum is m
1. Intuitive algorithm: enumerate each subset of S one by one and count the sum of elements in it.
- Iteration 2^n round
2- Subset is NP-complete
As far as the current calculation model is concerned, there is no algorithm that can answer this question in polynomial time
P21
P22
He calculated just as men breathe,
as eagles sustain themselves in the air.
— Francois Arago
eagles: Eagle
Two main tasks of algorithm analysis: correctness (invariance) × Monotonicity) + complexity.
Branch turn
Iterative cycle
Call + recursion (self call)
Main methods of complexity analysis:
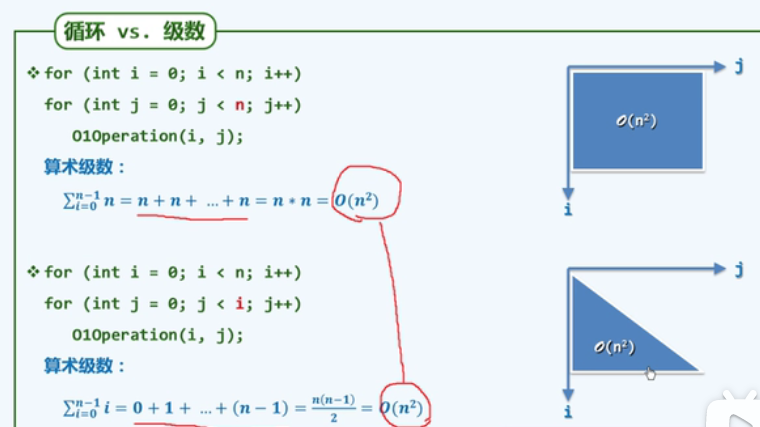
1. Iteration: summation of series
- (1) Arithmetic series: of the same order as the square of the last term
- (2) Power series: one order higher than the power
- (3) Geometric series (a > 1): of the same order as the last term.
- (4) Fractional series: O(1)
2. Recursion: recursive tracking + recursive equation
3. Guess + verify
P24 cycle
Rectangular area
Example: take non extreme elements
Question:
Given integer subset S, | s | = n > = 3
Find the element a ∈ S, a ≠ max(S) and a ≠ min(S)
Example: bubble sorting
Problem: given n integers, arrange them in (non descending) order.
method:
Scan exchange: compare each pair of adjacent elements in turn and exchange them if necessary
/* Bubble sorting */
void bubblesort(int A[], int n) {
for (bool sorted = false; sorted = !sorted;n--) /* Flipping and self subtraction*/
for(int i=1; i< n; i++)
if (A[i - 1] > A[i]){
swap(A[i - 1], A[i]);
sorted = false; // Clear global order flag
}
}
- 1. Invariance: after K rounds of scanning and exchange, the largest k elements must be in place
- 2. Monotonicity: after k rounds of scanning and exchange, the scale of the problem is reduced to n-1
- 3. Correctness: after up to n scans, the algorithm must terminate and can give the correct solution
P27 back - of - the - envelope calculation
P29 iteration and recursion
Iteration is artificial, and recursion is the magic power.
To iterate is human, to recurse, divine.
Iteration is sometimes more efficient in practical applications
Governing the masses is like governing the few, so is the score.
The control of a large force is the same principle as the control of a few men:
it is merely a question of dividing up their numbers.
Divide and rule: divide a large scale into sub blocks
/* Array summation: iterations*/
/* Problem: calculate the sum of any n integers */
int SumI(int A[], int n) {
int sum = 0; // O(1) / / accumulator
for (int i = 0; i < n; i++) //O(n)
sum += A[i]; // O(1)
return sum; // O(1)
}
/* T(n) = O(n)
* S(n) = O(2)
*/
- Gradually erode and continuously reduce the effective scale of the problem
P30
Reduce - and - conquer - Two sub problems: one is ordinary, the other is scale reduction.
Ordinary problem: it refers to a problem that can give results directly without complex operation.
P31
/* Array summation: linear recursion*/
sum(int A[], int n) {
return (n < 1) ? 0 : sum(A, n - 1) + A[n - 1];
}
/*T(n) = O(1) * (n+1) = O(n) */
Recursive trace analysis
- Check each recursive instance and accumulate the required time (the calling statement itself is included in the corresponding sub instance), and the sum is the algorithm execution time.
Recursive tracing: applies only to concise recursive patterns
Recursive equation: more suitable for complex recursive mode
P32
- The last item is T(0)-0
Example: array inversion
Give array A[0, n] and reverse it
Unified interface: void reverse(int *A, int lo, int hi);
/* Array inversion */
/* 1,Recursive version */
if (lo < hi) // The parity of the problem scale remains unchanged, and two recursive bases are required
{
swap(A[lo], A[hi]); reverse(A, lo + 1, hi - 1);
}
else return;
/* Iterative primitive method */
next:
if (lo < hi) {
swap(A[lo], A[hi]); lo++; hi--; goto next;
}
/* 3, Iterative compact */
while (lo < hi) swap(A[lo++], A[hi--]);
P34 divide and rule
Divide - and - conquer
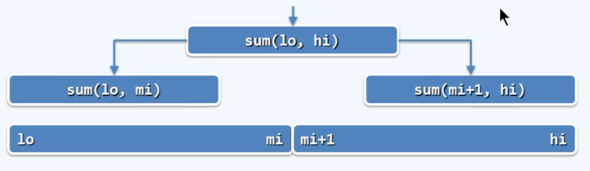
In order to solve a large-scale problem, it can be divided into several subproblems with roughly the same scale. The subproblems are obtained respectively, and the solution of the original problem is obtained from the solution of the subproblem.
/* Array summation: bisection recursion*/
sum(int A[]. int lo, int hi) {//Interval range A[lo, hi]
if (lo == hi) return A[lo];
int mi = (lo + hi) >> 1;
return sum(A, lo, mi) + sum(A, mi + 1, hi);
}// The entry form is sum(A, 0, n-1)
P36
Example: the two largest numbers
Find the two largest integers A[x1] and A[x2] from the array interval A[lo, hi], and A[x1] ≥ A[x2]
/* top 2 element in array*/
void max2(int A[], int lo, int hi, int& x1, int& x2) {
for (x1 = lo, int i = lo + 1; i < hi; i++)
if (A[x1] < A[i]) x1 = i;
for (x2 = lo, int i = lo + 1; i < x1; i++) /* Scan A[lo, x1]*/
if (A[x2] < A[i]) x2 = i;
for (int i = x1 + 1, i < hi; i++) /* Scan A[x1, hi]*/
if (A[x2] < A[i]) x2 = i;
}
/* T(n) = O(2n-3)*/
/* Improvement: maintain two pointers */
void max2(int A[], int lo, int hi, int& x1, int& x2) {
if (A[x1 = lo] < A[x2 = lo + 1]) swap(x1, x2);
for (int i = lo + 2; i < hi; i++)
if (A[x2] < A[i]) // Compare with x2 first
if (A[x1] < A[x2 = i])
swap(x1, x2);
}
/* Best case: 1 + (n-2) *1 = n-1
* Worst case: 1 + (n-2) * 2 = 2n-3
*/
P37 recursion + divide and conquer
/* Max2: Recursion + divide and conquer */
void max2(int A[], int lo, int hi, int& x1, int& x2) {
if (lo + 2 == hi) { /*...*/; return; }
if (lo + 3 == hi) {/*...*/; return; }
int mi = (lo + hi) / 2;
int x1L, x2L; max2(A, lo, mi, x1L, x2L);
int x1R, x2R; max2(A, mi, hi, x1R, x2R);
if (A[x1L] > A[x1R]) {
x1 = x1L; x2 = (A[x2L] > A[x1R]) ? x2L : x1R;
}
else {
x1 = x1R; x2 = (A[x1L] > A[x2R]) ? x1L : x2R;
}
}
Algorithm: iteration and recursion
Algorithm strategy: resolve - and - conquer, divide-and-conquer
Analysis: Recurrence trace, Recurrence
Supplementary knowledge points (important):
Recursive basis: it is an ordinary case of recursive function. Only recursive basis, recursion will not continue all the time.
Reduction and treatment:
- Recursive instances are: 1 instance with scale n, 1 instance with scale n-1, 1 instance with scale n-2,..., N in total
divide and rule
- Recursive instances are: 1 instance with scale n, 2 instances with scale n/2, 4 instances with scale n/4,..., with a total of 1 + 2 + 4 + 8 +... + n.
P38
Make it work,
make it right,
make it fast.
—Kent Beck
The first two: it can be realized by recursion
fast uses iteration.
int fib(n) { return (2 > n) ? n : fib(n - 1) + fib(n - 2); }
/*T(n) = O(2^n) */
P41
Going up stairs is similar
P42
1. Memory: memoization (tabulate the results of calculated examples for future reference)
2. Dynamic programming (from small to large, from bottom to top): dynamic programming
Reverse the calculation direction: from top-down recursion to bottom-up iteration.
f = 0; g = 1; // fib(0), fib(1)
while (0 < n--) {
g = g + f;
f = g - f;
}
return g;
/* T(n) = O(n), And only O(1) space is required */
Example: longest common subsequence
Subsequence: it is composed of several characters in the sequence according to the original relative order.
P44
Recursive T(n) = O(n^2)
Dynamic programming: T(n) = O(n*m)
1. List all sub questions (hypothetically) in one table
2. Reverse the calculation direction and calculate all items at one time from LCS(A[0], B[0])
P Limited (school online)
Limitations: caching
Why not learn poetry; If you don't learn etiquette, how can you stand
He has given signs of himself which are visible to those who seek, and not to those who do not seek him.
P cyclic shift
Problem: only use O(1) auxiliary space to move the elements in array A[0, n] by k units to the left.
void shift(int* A, int n, int k);
void shift0(int* A, int n, int k)//Move left repeatedly at intervals of 1
{
while (k--) shift(A, n, 0, 1);
}// K iterations in total, O(n*k)
int shift(int* A, int n, int s, int k) {
int b = A[s]; int i = s, j = (s + k) % n; int mov = 0; //mov recording times
while (s != j) // Starting from A[s], shift k bits to the left in turn with K as the interval
{
A[i] = A[j]; i = j; j = (j + k) % n; mov++;
}
A[i] = b; return mov + 1; //Finally, the starting element is transferred to the corresponding position
}
/* Iterative version */
void shift1(int* A, int n, int k) {
for (int s = 0, mov = 0; mov < n; s++)
mov += shift(A, n, s, k);
}// Move K positions and rotate in a circle with k elements apart
P flip
/* Inverted version */
// With the help of the inversion function, the array is rotated to the left by K bits
void shift2(int* A, int n, int k) {
reverse(A, k); // O(3k/2)
reverse(A + k, n - k); // O(3(n-k)/2)
reverse(A, n); // O(3n/2)
}// O(3n)
Continuous access to Cache
- The data access order shall be as close as possible
Supplementary notes:
1. The Hailstone problem has not been proved so far, that is, no one has proved that the Hailstone(n) process can be terminated for all positive integers.
2. Turing machine is an ideal calculation model, and its paper tape is an infinite paper tape with infinite extension at both ends.
3. Reduction and Governance: it is divided into two subproblems: an ordinary and a reduced scale.
The time complexity of calculating fib(n) recursively by definition is O(2^n)
Chapter 2 vector
P48
Linear sequence: Vector + List
Abstract Data Type(ADT)
Vector:
The types of elements are not limited to basic types.
P50
Ordered vector:
search(a), if any, directly returns the rank of the element; If it does not exist, it is not greater than the rank of the maximum value in the element of element a. If element a is less than all elements, return - 1.
/* Vector template class */
typedef int Rank; // Rank
#define DEFAULT_ Capability 3 / / default initial capacity
template<typename T> class Vector {//Vector template class
private: Rank_size; int _capacity; T* _elem; // Scale, capacity, data area
protected:
/* ... Internal function */
public:
/* ... Constructor*/
Vector(int c = DEFAULT_CAPACITY) {
_elem = new T[_capacity = c]; _size = 0;
}// default
Vector(T const* A, Rank lo, Rank hi)//Array interval copy
{
copyFrom(A, lo, hi);
}
Vector(Vector<T> const& V, Rank lo, Rank hi) //Vector interval replication
{
copyFrom(V._elem, lo, hi);
}
Vector(Vector<T> const& V) {
copyFrom(V._elem, 0, V._size); //Vector global copy
}
/* ... Destructor*/
~Vector() { delete[] _elem; } // Free up internal space
/* ... Read only interface*/
/* ... Writable interface*/
/* ... Traversal interface*/
};
/*********** Copy*******************/
template <typename T> // T is the basic type, or the assignment operator has been overloaded
void Vector<T>::copyFrom(T* const A, Rank lo, Rank hi) {
_elem = new T[_capacity = 2 * (hi - lo)]; //Allocate space
_size = 0; //Scale clearing
while (lo < hi)
_elem[_size++] = A[lo++]; //Copy to_ elem[0, hi-lo]
}
P53 extensible vector
Static space management
Insufficient:
- Overflow
- Underflow: there are few elements in a vector. Filling factor (_size / _capacity) < 50%
P54 dynamic space management
Cicada: when you grow up, shed your skin first
template <typename T>
void Vector<T>::expand() {// Capacity expansion when vector space is insufficient
if (_size < _capacity) return; //It's not full yet, so there's no need to expand the capacity
_capacity = max(_capacity, DEFAULT_CAPACITY); //Not less than the minimum capacity
T* oldElem = _elem; _elem = new T[_capacity <<= 1]; // Double capacity
for (int i = 0; i < _size; i++)// Copy original vector content
_elem[i] = oldElem[i]; //T is a basic type, or the assignment operator '=' has been overloaded
delete[] oldElem; //Release the original space
}
/* The vector is encapsulated, and there will be no wild pointer*/
P55
Reasons for adopting the "capacity doubling" strategy:
Other strategies, too many expansion times, increase the time cost.
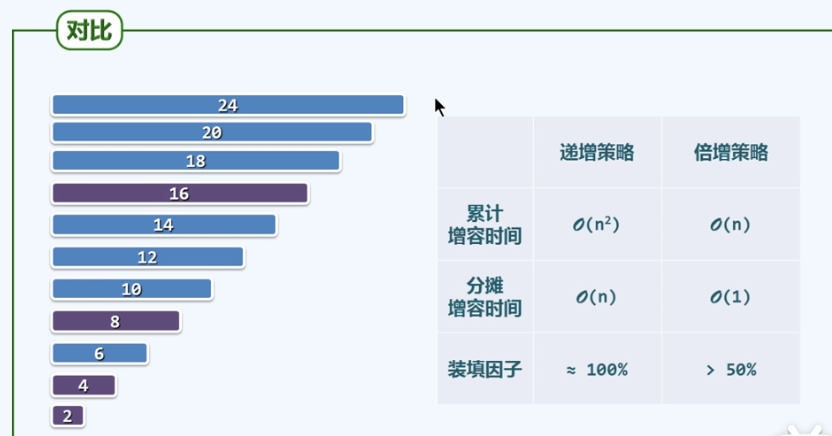
Blue: increasing; Purple ": double (sacrificing space for time)
P57 allocated complexity
P59
Element access
- V.get( r )
- V.put(r, e)
- A[r]
/* Overloaded subscript operator "[]"*/
template <typename T> // 0 <= r <= _size
T& Vector<T>:: operator[](Rank r) const { return _elem[r]; }
P60
/* Vector Insert operation */
template <typename T> // e is inserted as an element with rank r, 0 < = R < = size
Rank Vector<T>::insert(Rank r, T const& e) {
expand(); // If necessary, expand the capacity
for (int i = _size; i > r; i--) // From back to front
_elem[i] = _elem[i - 1] // Subsequent elements move backward one cell in sequence.
_elem[r] = e; _size++; // Insert new elements and update capacity
return r; // Return rank
}
P61
/* Vector: Interval deletion */
template <typename T> // Delete interval [lo, HI), 0 < = Lo < = hi < = size
int Vector<T>::remove(Rank lo, Rank hi) {
if (lo == hi) return 0; // Degradation is treated separately for efficiency reasons
while (hi < _size) _elem[lo++] = _elem[hi++]; // [hi, _size) move the hi Lo bit forward in sequence
_size = lo; shrink(); // Update the scale and reduce the volume if necessary
return hi - lo;
}
P62 single element deletion
/* Single element deletion */
template <typename T >// Delete the element with rank r in the vector, 0 < = R < = size
T Vector<T>::remove(Rank r) {
T e = _elem[r]; // Backup deleted elements
remove(r, r + 1); // Call interval deletion method
return e; // Returns the deleted element
}
P63 find
/*Vector operations: finding */
template <typename T>
Rank Vector<T>::find(T const& e, Rank lo, Rank hi) const {
while ((lo < hi--) && e != _elem[hi]); // Reverse search
return hi;
}
Input sensitivity: best O(1), worst O(n)
P64
/* Vector Operation: weight removal */
template <typename T>
int Vector<T>::deduplicate() {
int oldSize = _size;
Rank i = 1;
while (i < _size) // Examine the elements one by one from front to back_ elem[i]
(find(_elem[i], 0, i) < 0) ?// Find the same person in the prefix
i++
: remove(i);
return oldSize - _size; // Total number of elements deleted
}
/* O(n^2)*/
Optimization ideas:
1. Following the idea of the efficient version of unify (), the number of element moves can be reduced to O(n), but the comparison number is still O(n^2); Moreover, the stability is destroyed
2. Mark the duplicate elements to be deleted first, and then delete them uniformly. The stability is maintained, but the search length is longer, resulting in more comparison operations.
3,V.sort().uniquify(), O(nlogn)
P65
/* Vector Operations: traversal */
/* Method 1: use the function pointer mechanism to read only or modify locally*/
template <typename T>
void Vector<T>::traverse(void (*visit)(T&)) //Function pointer
{
for (int i = 0; i < _size; i++) visit(_elem[i]);
}
/* Method 2: use the function object mechanism to modify globally */
template <typename T>template <typename VST>
void Vector<T>::traverse(VST& visit)// Function object
{
for (int i = 0; i < _size; i++) visit(_elem[i]);
}
/* Implement a class that adds one to a single T-type element */
template <typename T>
struct Increase {// Function object: implemented by overloading the operator "()"
virtual void operator()(T& e) { e++; }
};
template <typename T> void increase(Vector<T>& V) {
V.traverse(Increase<T>()); // Ergodic vector
}
P66:
In an ordered sequence, the order of any pair of adjacent elements
In an unordered sequence, there is always a pair of adjacent elements in reverse order
template <typename T>// Returns the total number of adjacent elements in reverse order
int Vector<T>::disordered() const {
int n = 0;
for (int i = 1; i < _size; i++) // Check each pair of adjacent elements one by one
n += (_elem[i - 1] > _elem[i]); // Count in reverse order
return n;
}
P67 ordered weight removal
- Each interval only needs to retain a single element
/* Vector: Order + weight removal */
template <typename T> int Vector<T>::uniquify() {
int oldSize = _size; int i = 0;
while (i < _size - 1)// Go from front to back and compare the adjacent elements one by one
(_elem[i] == _elem[i + 1]) ? remove(i + 1):i++; // If the same, delete the latter; Otherwise, go to the next element
return oldSize - _size; // Total number of elements deleted
}
/* Low efficiency: O(n^2) */
P69
- Delete the deleted elements as a whole and delete them in batches
/* Method 2: order + de duplication */
template <typename T> int Vector<T>::uniquify() {
Rank i = 0; j = 0;
while (++j < _size) // Scan one by one until the last element
if (_elem[i] != _elem[j])
_elem[++i] = _elem[j];
_size = ++i; shrink(); // Directly cut off the redundant elements in the tail
return j - i; // Total number of deleted elements
}
/* O(n) */
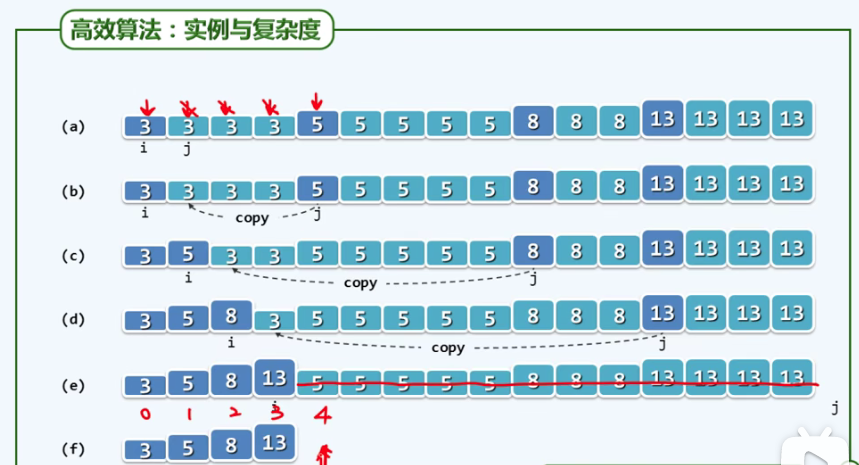
Ordered vector, binary search
/* Unified interface */
template <typename T>// Search algorithm unified interface 0 < = Lo < hi<=_ size
Rank Vector<T>::search(T const& e, Rank lo, Rank hi) const {
return (rand() % 2) ?
binSearch(_elem, e, lo, hi) // Binary search algorithm
: fibSearch(_elem, e, lo, hi); // Fibonacci search algorithm
}
P73
template<typename T> // Find elements in ordered vector interval [lo, hi]
static Rank binSearch(T* A, T const& e, Rank lo, Rank hi) {
while (lo < hi) {
Rank(mi = (lo + hi) >> 1);
if (e < A[mi]) hi = mi; // Small tips: use the less than sign, which is the same as the actual position for easy understanding
else if (A[mi] < e) lo = mi + 1;
else return mi;
}
return -1; // Search failed
}
P77
template <typename T>
static Rank fibSearch(T* A, T const& e, Rank lo, Rank hi) {
Fib fib(hi - lo);
while (lo < hi) {
while (hi - lo < fib.get()) fib.prev();
Rank mi = lo + fib.get() - 1; // Golden ratio
if (e < A[mi]) hi = mi;
else if (A[mi] < e) lo = mi + 1;
else return mi;
}
return -1;
}
P83
template <typename T> static Rank binSearch(T* A, T const& e, Rank lo, Rank hi) {
while (1 < hi - lo) {// The algorithm will not terminate until the width of the effective search interval is reduced to 1
Rank mi = (lo + hi) >> 1;
(e < A[mi]) ? hi = mi : lo = mi; //[lo, mi) or [MI, HI) / * MI is included in the right section*/
}// At exit, hi = lo + 1, and the search interval contains only one element A[lo]
return (e == A[lo]) ? lo : -1; // Returns the rank of the hit element or - 1
}
P84
/* Version C */
template <typename T> static Rank binSearch(T* A, T const& e, Rank lo, Rank hi) {
while (lo < hi) {// A[0, lo) <= e < A[hi, n)
Rank mi = (lo + hi) >> 1;
(e < A[mi]) ? hi = mi : lo = mi + 1; // [lo,mi) or (mi, hi)
}// At exit, A[lo=hi] is the largest element greater than e
return --lo; // Therefore, lo-1 is the maximum rank of elements not greater than e
}
Correctness: invariance + monotonicity
- Invariance: a [0, Lo) < = e < a [Hi, n)
P87: ordered, interpolation search
- Interpolation Search
Worst case: O(n), not satisfying uniform independent distribution
Best case: a little test is medium, and the first test is medium.
Average situation: after each comparison, n is reduced to n^0.5
P90
It is applicable to the case where the search interval is very large or the comparison operation cost is very high.
Feasible methods:
Firstly, the search range is reduced to a certain range through interpolation search, and then binary search is carried out.
Large scale: interpolation lookup
Medium scale: half search
Small scale: sequential lookup
If the vector elements are arranged in order, the computational efficiency will be greatly improved
/* Sorter: unified interface*/
template <typename T>
void Vector<T>::sort(Rank lo, Rank hi) {// Interval [lo,hi)
switch (rand() % 5) {
case 1: bubbleSort(lo, hi); break; // Bubble sorting
case 2: selectionSort(lo, hi); break; // Select sort
case 3: mergeSort(lo, hi); break; // Merge sort
case 4: heapSort(lo, hi); break; // Heap sort
default: quickSort(lo, hi); break; // Quick sort
}
}
bubble sort
For each scan exchange, record whether there are elements in reverse order. If it exists, if and only as over exchange.
template <typename T> void Vector<T>::bubbleSort(Rank lo, Rank hi)
{
while (!bubble(lo, hi--)); // Scan and exchange one by one until the sequence is complete
}
/* improvement */
template <typename T> bool Vector<T>::bubble(Rank lo, Rank hi) {
bool sorted = true; // Overall order sign
while(++lo < hi)// From left to right, check each pair of adjacent elements one by one
if (_elem[lo - 1] > _elem[lo]) {//If in reverse order, then
sorted = false; //It means that it has not been ordered as a whole and needs to be improved
swap(_elem[lo - 1], _elem[lo]); // exchange
}
return sorted;
}
P94
/* Further improvement */
template <typename T> Rank Vector<T>::bubble(Rank lo, Rank hi) {
Rank last= lo; // The rightmost reverse pair is initialized to [lo-1, lo]
while(++lo < hi)// From left to right, check each pair of adjacent elements one by one
if (_elem[lo - 1] > _elem[lo]) {//If in reverse order, then
last = lo; //Update the position record of the rightmost reverse sequence pair, and
swap(_elem[lo - 1], _elem[lo]); // exchange
}
return last;// Returns the rightmost reverse pair position
}
/* T(n) = O(n) */
Stability of algorithm
Whether the relative order of repeating elements in the input and output sequence remains unchanged.
- Bubble sorting is stable
- Worst case O(n^2)
P97 merge sort
template<typename T>
void Vector<T>::mergeSort(Rank lo, Rank hi) {// [lo, hi)
if (hi - lo < 2) return; // Natural order of unit interval
int mi = (lo + hi) >> 1;
mergeSort(lo, mi); // Sort the first half
mergeSort(mi, hi); // Sort the second half
merge(lo, mi, hi); // Merge
}
/* Two way merging */
/* Merge two ordered sequences into one ordered sequence:
* S[lo, hi) = S[lo, mi) + S[mi, hi)
*/
template<typename T> void Vector<T>::merge(Rank lo, Rank mi, Rank hi) {
T* A = _elem + lo; // Combined vector a [0, hi LO) = _elem [lo, HI)
int lb = mi - lo; T* B = new T[lb]; // Front sub quantity B[0, lb) = _elem[lo, mi)
for (Rank i = 0; i < lb; B[i] = A[i++]); // Sub vector B before copy
int lc = hi - mi; T* C = _elem + mi; // Latter sub vector C [0, LC] =_ elem[mi, hi)
for (Rank i = 0, j = 0, k = 0; (j < lb) || (k < lc)) {// B[j] and C[k] go to the end of A
if ((j < lb) && (lc <= k || (B[j] <= C[k]))) A[i++] = B[j++]; // C[k] is no longer or not small
if ((k < lc) && (lb <= j || (C[k] < B[j]))) A[i++] = C[k++]; // B[j] no more or greater
}
delete[] B; // Release temporary space B
}
/* The second half element C does not need to be newly opened */
/* Short circuit evaluation: (LC < = k | (B [J] < = C [k]))*/
/* Improvement: if B completes traversal in advance, the program can be terminated directly*/
for (Rank i = 0, j = 0, k = 0; j < lb) {
if ((k < lc) && (C[k] < B[j])) A[i++] = C[k++];
if (lc <= k || (B[j] <= C[k])) A[i++] = B[j++];
} // Exchange the order of two sentences in the loop and delete the redundant logic
P bitmap (school online)
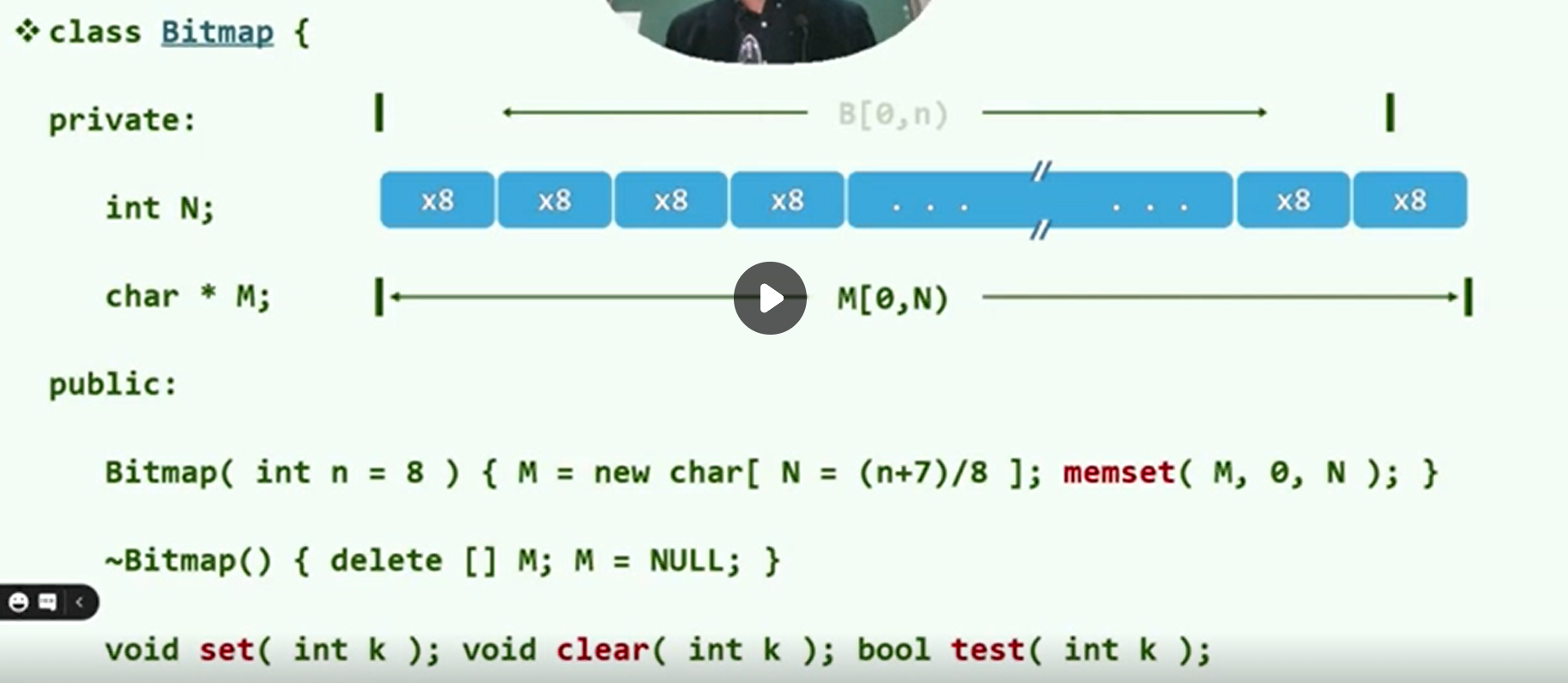
Small collection + big data
duplicate removal
screen
P supplementary notes
- The space complexity of recursive version is equal to the maximum recursive depth
2. The result of allocating complexity is lower than the average complexity( ×): The results of apportionment complexity and average complexity are not necessarily related.
3. The return value of the disordered() algorithm is the number of adjacent pairs in reverse order.
4. If the distribution of elements in the (ordered) vector satisfies the independent uniform distribution (before sorting), the average time complexity of interpolation search is O(loglog(n))
Chapter III list
P103-P107
Don't lose the link.
—Robin Milner
Precursor: predecessor
successor: success
First node: first/front
End node: last/rear
Vector: call by rank
List: call by position
/* List node: ListNode template class */
#Define posi (T) listnode < T > * / / list node location
template<typename T>
struct ListNode {// List node template class (implemented in the form of two-way linked list)
T data; // numerical value
Posi(T) pred; // precursor
Posi(T) succ; // Successor
ListNode() {} // Construction for header and tracker
ListNode(T e, Posi(T) p = NULL, Posi(T) s = NULL)
: data(e), pred(p), succ(s) {} // default constructor
Posi(T) insertAsPred(T const& e); // Front insertion
Posi(T) insertAsSucc(T const& e); // Post insert
};
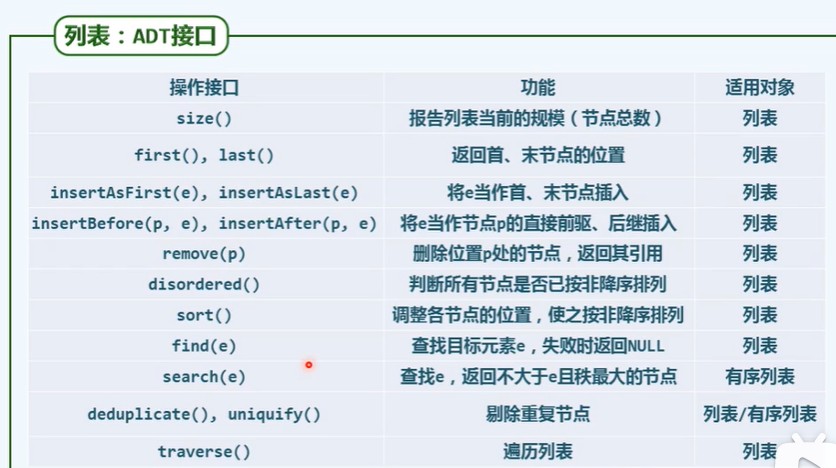
/* List: list template class*/
#include "listNode.h" / / introduce the list node class
template<typename T> class List {// List template class
private: int _size; // scale
Posi(T) header; Posi(T) trailer; // Head and tail sentry
protected:/* ...Internal function*/
public: /* ...Constructor, destructor, read-only interface, writable interface, traversal interface*/
};
- The rank of head, head, end and tail nodes can be understood as - 1, 0, n-1, n respectively
/* structure */
template <typename T> void List<T>::init() {// Initialization, which is called uniformly when creating list objects
header = new ListNode<T>; // Create head sentry node
trailer = new ListNode<T>; // Create tail sentinel node
header->succ = trailer; header-> pred = NULL:
trailer->pred = header; trailer->succ = NULL; // interconnection
_size = 0; // scale
}
-P111 unordered list
P107 rank based access list
Overloaded subscript operator
template <typename T>
T List<T>::operator[](Rank r) const {
Posi(T) p = first();
while (0 < r--) p = p->succ; // The r-th node in sequence is]
return p->data; // Target node
}// The rank of any node, that is, the total number of its precursors
P108 find
/* Among the n (true) precursors of node P (possibly trailer), find the last one equal to e*/
template<typename T>// When calling from outside, 0 < = n < = rank (P) <_ size
Posi(T) List<T>::find(T const& e, int n, Posi(T) p) const {//Sequential search
while (0 < n--) // From right to left, compare the precursors of p with e one by one
if (e == (p = p->pred)->data) return p; // Until hit or range out of bounds
return NULL;
}
P109
/* insert */
template<typename T> Posi(T) List<T>::insertBefore(Posi(T) p, T const& e)
{
_size++; return p->insertAsPred(e); // e is inserted as the precursor of p
}
template<typename T> // Pre insertion algorithm
Posi(T) ListNode<T>::insertAsPred(T const& e) {
Posi(T) x = new ListNode(e, pred, this);
pred->succ = x; pred = x; return x; // Establish a link and return the location of the new node
}
/* Replication based construction */
template <typename T> // Basic interface
void List<T>::copyNodes(Posi(T) p, int n) {
init(); // Create and initialize the head and tail sentry nodes
while (n--) // Insert the n items from p as the end node in turn
{
insertAsLast(p->data); p = p->succ;
}
}
/* insertBefore(trailer)*/
P110 delete
/* delete */
template <typename T>
T List<T>::remove(Posi(T) p) { // O(1)
T e = p->data; // Backup the value of the node to be deleted, which is used to return
p->pred->succ = p->succ;
p->succ->pred = p->pred;
delete p; _size--; return e; // Return backup value
}
/* Delete list */
// Deconstruction
template <typename T> List<T>::~List() // List destructor
{
clear(); delete header; delete trailer; // Clear the list and release the head and tail sentry nodes
}
template<typename T> int List::clear() {// clear list
int oldSize = _size;
where(0 < _size)// Delete the first node repeatedly until the list becomes empty
remove(header->succ);
return oldSize;
}// O(n), linearly proportional to the list size
P111 de duplication (uniqueness)
/* Uniqueness */
template <typename T> int List<T>::deduplicate() {// Delete duplicate nodes in unordered list
if (_size < 2) return 0;
int oldSize = _size;
Posi(T) p = first(); Rank r = 1; // p starts from the first node
while (trailer != (p = p->succ)) {//
Posi(T) q = find(p->data, r, p); // In the first r (true) precursors of p, find the same one
q ? remove(q): r++; // If it does exist, delete it, otherwise the rank increases
}
return oldSize - _size; // Total number of elements deleted
}
-P114 has a sequence table
P112
/* Ordered lists: uniqueness*/
template<typename T>int List<T>::uniquify() {// Eliminate duplicate elements in batches
if (_size < 2) return 0;
int oldSize = _size; //Record the original scale
ListNodePosi(T) p = first(); ListNodePosi(T) q; // p is the starting point of each section and q is its successor
while (trailer != (q = p->succ)) // Repeatedly examine the adjacent node pairs (p, q)
if (p->data != q->data) p = q; // If they are different, turn to the next section
else remove(q); // Otherwise, delete the latter
return oldSize - _size; // Total number of deleted elements
}// Just traverse the whole list once, O(n)
P114
/* Ordered lists: finding */
template <typename T> // Among the n (true) precursors with node p in the sequence table, find the last one not greater than e
Posi(T) List<T>::search(T const& e, int n, Posi(T) p) const {
while (0 <= n--) // For the nearest n precursors of p, from right to left
if (((p = p->pred)->data) <= e) break; //Compare one by one
return p; // Return to the location where the search ends until the hit, value or range is out of range
}// Best O(1), worst O(n)
RAM: rank based access
Turing machine ™: call-by-position
List sorting algorithm
-P120 select sort
- Select the largest
- Bubblesort also has a similar idea. The essence of scanning and exchange is to find the biggest. Worst O(n^2)
/* Select and sort n consecutive elements starting from position p in the list, valid (p) & & rank (p) + n < = size*/
template <typename T> void List<T>::selectionSort(Posi(T) p, int n) {
Posi(T) head = p->pred; Posi(T) tail = p; // Range to be sorted (head, tail)
for (int i = 0; i < n; i++) tail = tail->succ; // head/tail may be a head/tail sentry
while (1 < n) { // Repeatedly find the largest one from the interval to be sorted and move it to the front of the ordered interval
insertBefore(tail, remove(selectMax(head->succ, n)));
tail = tail->pred; n--; // The range of the to be sorted interval and the ordered interval are updated synchronously
}
}
new and delete are 100 times the actual value and should be avoided as far as possible
Improvement idea: when the element is the precursor of the last element, there is no need to move. But in fact, the probability of this situation is very low, and such improvement is not worth the loss.
template<typename T> // Select the largest one from the n elements starting at position p, 1 < n
Posi(T) List<T>::seletMax(Posi(T) p, int n) {
Posi(T) max = p; // The maximum value is tentatively determined as p
for (Posi(T) cur = p; 1 < n; n--)// Subsequent nodes are compared with max one by one
if (!lt((cur = cur->succ)->data, max->data)) // If > = max / *! lt: not less than . Comparator*/
max = cur; // Update the maximum element position record / * take the equal sign to take the later one when there are duplicate elements*/
return max; // Return maximum node position
}
Improvement: the number of element moves is far less than bubble sorting
-P128 insert sort
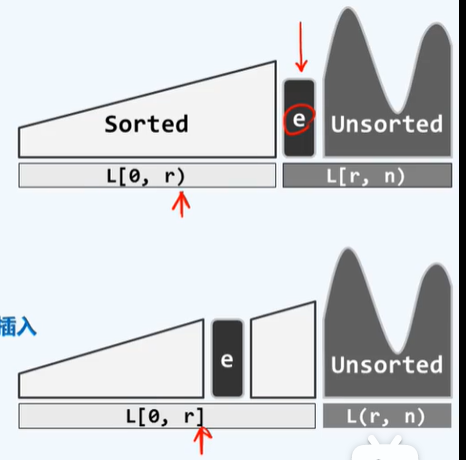
1. Search of ordered sequence
2. Insertion of ordered sequence
/* Insert and sort n consecutive elements starting from position p in the list, valid (p) & & rank (p) + n < = size*/
template<typename T> void List<T>::insertionSort(Posi(T) p, int n) {
for (int r = 0; r < n; r++) {// Each node is introduced one by one, and S(r+1) is obtained from Sr
insertAfter(search(p->data, r, p), p->data); // Find + insert
p = p->succ; remove(p->pred); // Turn to the next node
}// n iterations, each time O(r+1)
} // Only O(1) auxiliary space is used, which belongs to in place algorithm
Best case: one comparison, 0 exchanges, O(n)
Worst case: each insertion is smaller than the row, O(n^2)
- Select sorting, the best and worst are O(n^2)
P127
The average time complexity of insertion sorting is O(n^2), which means that although the best case is O(n), the probability of this situation is very low.
P128 reverse sequence pair
- Input sensitive: insert sort, Hill sort
P129 exercise: LightHouse
divide and rule
Calculate inverse logarithm
Supplementary notes
1. For a two-way list, you can directly access p - > PRED to locate its direct precursor, which only takes O(1) time. For a one-way list, locating its direct precursor needs to access each node one by one from the first node. In the worst case, it needs to traverse the whole list, so it takes O(n) time.
2. The list with length n is equally divided into n/k segments, and the length of each segment is k. there is no reverse order of elements between different segments. The worst time complexity of inserting and sorting the list is O(nk)
Chapter 4 stack and queue
P130
A stack ADT and its implementation
-P132
Stack: a stack of chairs or plates
- Left stack top
- LIFO: last in first out
- Stack is a special case of sequence, which can be derived directly from vector or list
template<typename T> class Stack : public Vector<T> {//Derived from vector
public: // size(), empty() and other open interfaces can be used directly
void push(T const& e) { insert(size(), e); }// Push
T pop() { return remove(size() - 1); }// Out of stack
T& top() { return (*this)[size() - 1]; }// Take the top
};// Take the beginning / end of the vector as the bottom / top of the stack
C-ary conversion
-P159
/* Binary conversion */
void convert(Stack<char>& S, __int64 n, int base) {
static char digit[] = //The digit symbols under the new base system can be filled in appropriately according to the value range of base
{ '0','1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F' };
while (n > 0) {// From low to high, calculate the digits under the new base one by one
S.push(digit[n % base]); // Remainder stack
n /= base; // n is updated to its division of base
}
}
main() {
Stack<char> S; convert(S, n, base); // Use the stack to record the converted digits
while (!S.empty()) printf("%c", S.pop()); //Reverse order output
}
D bracket matching
-P141
- Eliminate a pair of adjacent left and right parentheses
Idea:
Sequential scan expression, using the stack to record the scanned part
- Repeated iteration: in case of (, enter the stack; in case of), exit the stack
/* parenthesis matching */
bool paren(const char exp[], int lo, int hi) {// exp[lo, hi)
Stack<char> S; // Use the stack to record the found but unmatched left parenthesis
for (int i = lo; i < hi; i++)// Check the current characters one by one
if ('(' == exp[i]) S.push(exp[i]); // In case of left parenthesis: stack
else if (!S.empty()) S.pop(); // In case of right parenthesis: if the stack is not empty, the left parenthesis will pop up
else return false; // In case of right parenthesis, the stack is empty and must not match
return S.empty(); //
}
Why not use a counter? In order to be easily extended to the coexistence of multiple parentheses.
Stack permutation
-P146
- Stack A containing elements, transition stack B, and stack B storing results
Different combinations of pop() and push() will get different results
Illegal stack shuffling:
S is empty before each S.pop(); Or the element to pop up is in s, but it is not the top element
Stack shuffling number
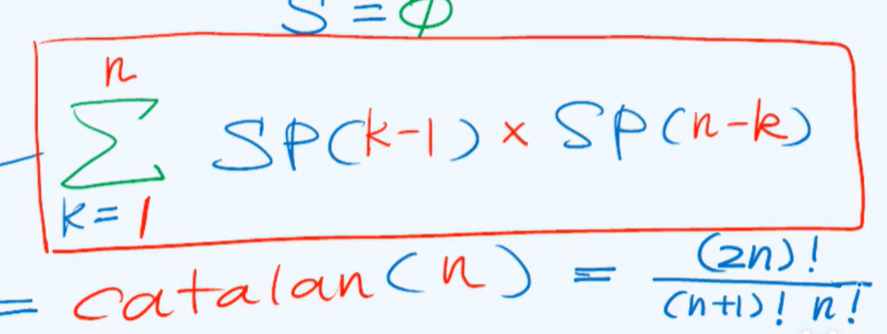
F infix expression
-P155
Stack + linear scan
/* Operation expression calculation */
float evaluate(char* S, char* RPN) {// Infix expression evaluation
Stack<float> opnd, Stack<char> optr; // Operand stack, operator stack
optr.push('\0'); // The tail sentry '\ 0' also enters the stack first as the head sentry
while (!optr.empty()) {// Process each character one by one until the operator stack is empty
if (isdigit(*S)) // If the current character is an operand, then
readNumber(S, opnd); // Read in (possibly multi bit) operand
else // If the current character is an operator, the priority between it and the operator at the top of the stack will be considered
switch (orderBetween(optr.top(), *S)) { /* handle separately */
}
}// while
return opnd.pop(); // Pop up and return the final calculation result
}
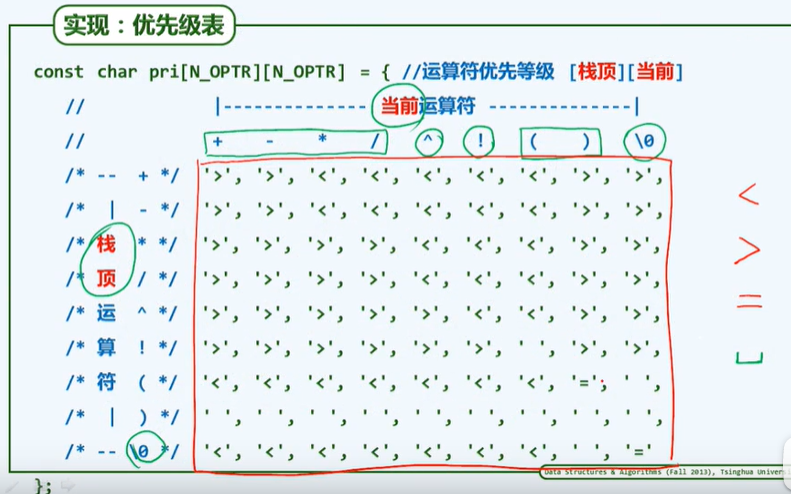
/* Implementation priority table */
const char pri[N_OPTR][N_OPTR]{// Operator priority
};
switch (orderBetween(optr.top(), *S)) {
case '<': // Lower stack top priority
optr.push(*S); S++; break; // The calculation is delayed, and the current operator is put on the stack
case '=': // Equal priority (the current operator is a closing parenthesis or a trailing sentinel '\ 0')
optr.pop(); S++; break; // Remove parentheses and receive the next character
case '>': { // The operator at the top of the stack has higher priority. The corresponding calculation is implemented and the results are put on the stack
char op = optr.pop(); // The stack top operator exits the stack and performs the corresponding operation
if ('!' == op) opnd.push(calcu(op, opnd.pop())); // Univariate calculation
else { float p0pnd2 = opnd.pop(), p0pnd1 = opnd.pop()； // Binary operator
opnd.push(calcu(p0pnd1, op, p0pnd2)); // Implement the calculation and put the results on the stack
}
break;
}
}
P152 - P155 operation example of the above code
G inverse Polish notation (RPN: Reverse Polish Notation)
-P159
Which operator appears first is calculated first
If you want to take it, you must give it first
Infix to postfix:
1. Priority is shown in parentheses
2. Move the operation symbol after the corresponding closing bracket
3. Erase all brackets
/* infix To postfix: conversion algorithm*/
float evaluate(char* S, char*& RPN) {// RPN conversion
while (!optr.empty()) {//Process each character one by one until the operator stack is empty
if (isdigit(*S)) // If the current character is an operand
{ readNumber(S, opnd); append(RPN, opnd.top()); } // Access RPN
else// If the current character is an operator
switch (orderBetween(optr.top(), *S)) {
case '>': {
char op = optr.pop(); append(RPN, op); //Access RPN
}
}
}
}
Queue ADT and its implementation
Badminton bucket, line up
- One end out, one end in
- be limited to:
Tail insertion: enqueue() + rear()
Delete header (front): dequeue() + front()
- FIFO: first in first out
Stack symmetry
The head of the team is on the right
Queues are special cases of sequences and can be derived from vectors or lists
/* queue */
template <typename T>class Queue : public List<T> {//Queue template class derived from list
public: // size() and empty() are used directly
void enqueue(T const& e) { insertAsLast(e); }// Join the team
T dequeue() { return remove(first()); } // Out of the team
T& front() { return first()->data; } // Team leader
}; // Take the beginning / end of the list as the head / end of the queue
Supplementary notes:
Exercise:
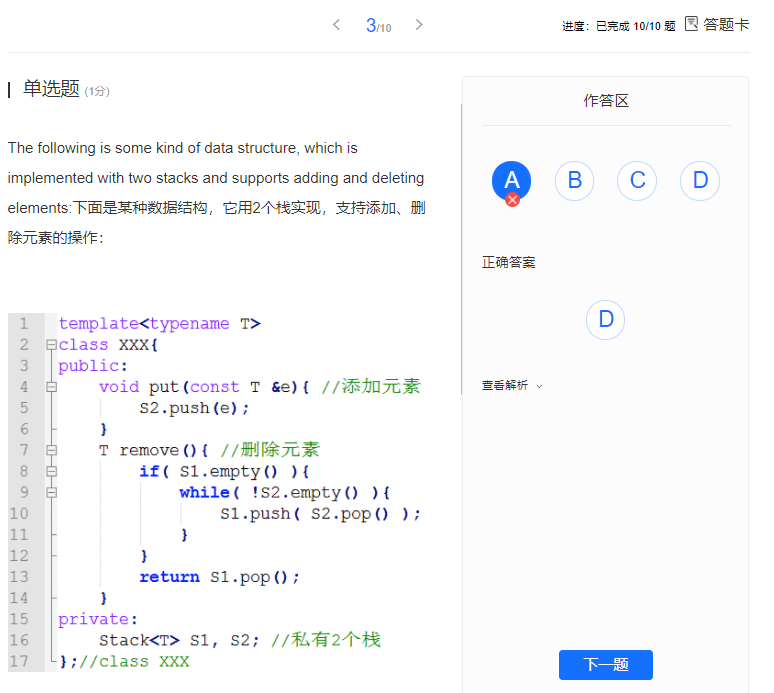
Select the "D" option???
Exercise 2:
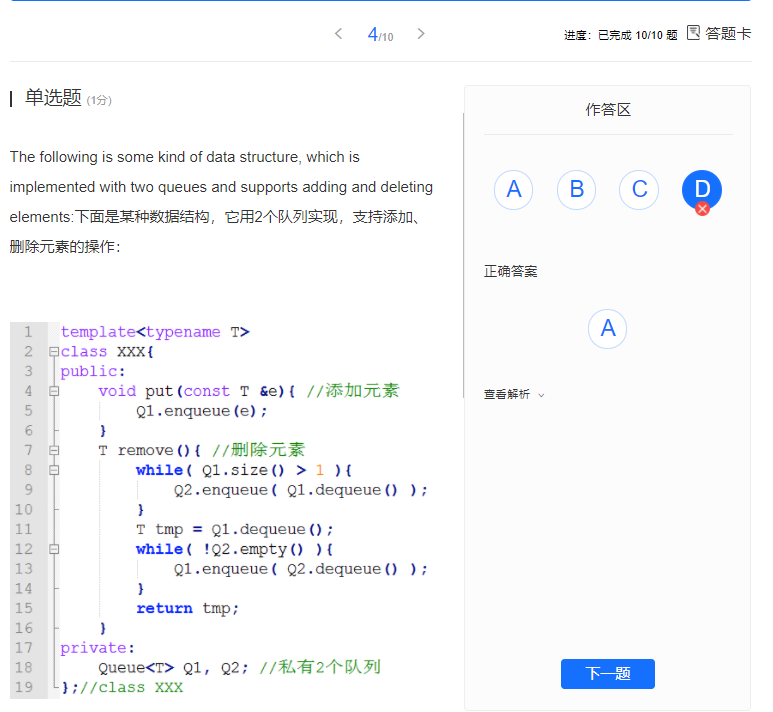
Select A???
Chapter 5 binary tree
A tree
-P169
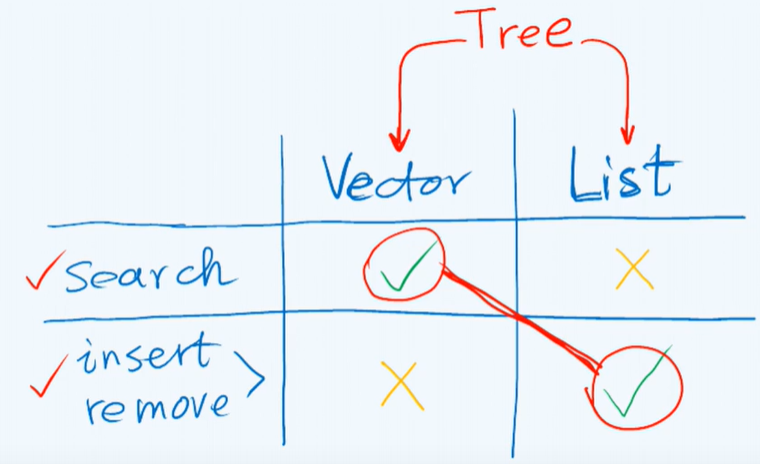
Tree: a list of lists. semilinear
- Hierarchical relationship
vertex , edge
A tree is a special graph T= (V, E), the number of nodes | V| = n, and the number of edges | E| = e
Child
Sibling
Father
Degree
P167:
access
Path length: number of sides
Connected graph
Acyclic graph
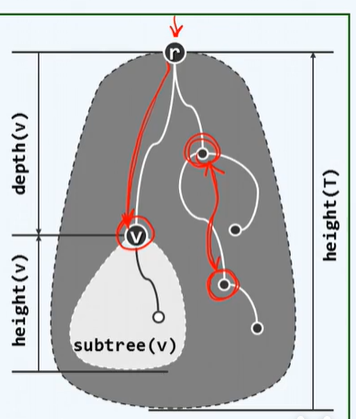
The height of the empty tree is taken as - 1
Representation of B-tree
P170
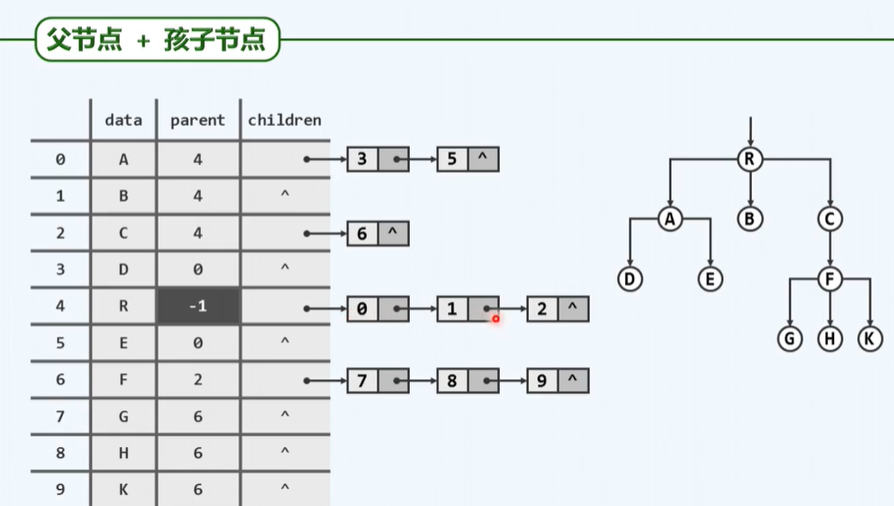
C binary tree
P175
D binary tree implementation
P178
/* BinNode template class */
#Define binnodeposi (T) binnode < T > * / / node location
template <typename T> struct BinNode {
BinNodePosi(T) parent, lChild, rChild; // Father, child
T data; int height; int size(); // Height and subtree size
BinNodePosi(T) insertAsLC(T const &); // Insert new node as left child
BinNodePosi(T) insertAsRC(T const&); // Insert new node as right child
BinNodePosi(T) succ(); //Direct successor of the current node (in the sense of middle order traversal)
template <typename VST > void travLevel(VST &); // Hierarchical traversal of subtree
template <typename VST > void travPre(VST &); // Subtree preorder traversal
template <typename VST > void travIn(VST &); // Order traversal in subtree
template <typename VST > void travPost(VST&); // Postorder traversal of subtree
};
/* BinNode Interface implementation */
template <typename T > BinNodePosi(T) BinNode<T>::insertAsLC(T const& e)
{
return lChild = new BinNode(e, this);
}// O(1)
template <typename T> BinNodePosi(T) BinNode<T>::insertAsRC(T const& e)
{
return rChild = new BinNode(e, this);
} // O(1)
template <typename T>
int BinNode<T>::size() { // The total number of offspring, that is, the size of the subtree with which it is rooted
int s = 1; // Count into itself
if (lChild) s += lChild->size(); // Recursive inclusion of left subtree size
if (rChild) s += rChild->size(); // Recursive right subtree size
return s;
}// O(n)
/* BinTree template class */
template <typename T> class BinTree {
protected:
int _size; // scale
BinNodePosi(T) _root; // Root node
virtual int updateHeight(BinNodePosi(T) x); // Update the height of node x
void updateHeightAbove(BinNodePosi(T) x); // Update the height of x and ancestors
public:
int size() const { return _size; } // scale
bool empty() const { return !_root; } // Air judgment
BinNodePosi(T) root() const { return _root; }// tree root
/* ... Subtree interface, delete and detach interface*/
/* ... Traverse interface*/
};
/* Height update */
# define stature(p) ((p)? (p) - > height: - 1) / / node height --- the agreed empty tree height is - 1
template <typename T> // Update the node x height. The specific rules vary from tree to tree
int BinTree<T>::updateHeight(BinNodePosi(T) x) {
return x->Height = 1 +
max(stature(x->lChild), stature(x->rChild));
}// The conventional binary tree rule, O(1), is adopted here
template <typename T> // Height of renewal v and its ancestors
void BinTree<T>::updateHeightAbove(BinNodePosi(T) x) {
while (x) // Can be optimized: once the height is surrounded, it can be terminated
{
updateHeight(x); x = x->parent;
}
}// O(n = depth(x))
/* Node insertion */
template <typename T> BinNodePosi(T)
BinTree<T>::insertAsRC(BinNodePosi(T) x, T const& e) {// insertAsLC symmetry
_size++; x->insertAsRC(e); // The height of ancestors may increase, and the other nodes must remain unchanged
updateHeightAbove(x);
return x->rChild;
}
E-preorder traversal
P183
/* Preorder traversal_ recursion*/
template <typename T, typename VST>
void traverse(BinNodePosi(T) x, VST& visit) {
if (!x) return;
visit(x->data);
traverse(x->lChild, visit);
traverse(x->rChild, visit);
}// T(n) = O(n)
/* Preorder traversal_ Iteration 1*/
template <typename T, typename VST>
void travPre_I1(BinNodePosi(T) x, VST& visit) {
Stack <BinNodePosi(T)> S; // Auxiliary stack
if (x) S.push(x); // Root node stack
while (!S.empty()) {// Loop repeatedly before the stack becomes empty
x = S.pop(); visit(x->data); // Pop up and access the current node
if (HasRChild(*x)) S.push(x->rChild); // Right child first in and then out
if (HasLChild(*x)) S.push(x->lChild); //Left child rear in first out
}
}
/* Preorder traversal_ Iteration 2*/
template <typename T, typename VST>// Apportionment O(1)
static void visitAlongLeftBranch(
BinNodePosi(T) x,
VST& visit,
Stack <BinNodePosi(T)>& S) {
while (x) {// Repeatedly
visit(x->data); // Access current node
S.push(x->rChild); // Right child (right subtree) into the stack (out of the stack in reverse order in the future)
x = x->lChild; // Down the left chain
}
}
/* Main algorithm */
void travPre_I2(BinNodePosi(T) x, VST& visit) {
Stack <BinNodePosi(T)> S; // Auxiliary stack
while (true) {//Access nodes batch by batch in the unit of (right) subtree
visitAlongLeftBranch(x, visit, S); // Access the left chain of subtree x and put the right subtree into the stack buffer
if (S.empty()) break; // Exit when stack is empty
x = S.pop(); // Pop up the root of the next subtree
}
}
The order of first order traversal is: first access the nodes on the left chain from top to bottom, and then access their right subtree from bottom to top.
Inorder traversal in F
P192
/* Middle order traversal_ recursion*/
template <typename T, typename VST>
void traverse(BinNodePosi(T) x, VST& visit) {
if (!x) return;
traverse(x->lChild, visit);
visit(x->data);
traverse(x->rChild, visit);
}
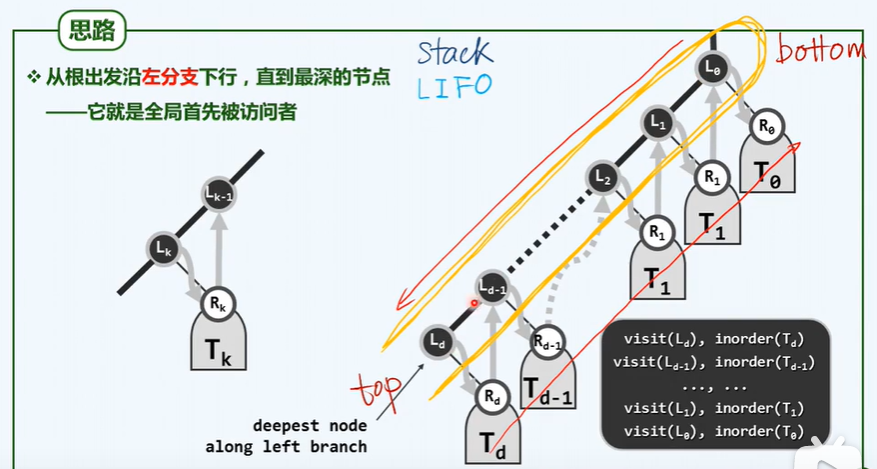
/* Middle order traversal_ iteration */
/* Start from the root node and humiliate the left chain of control until a node has no left node (the point of access)*/
/* Access the left chain node -- > traverse the right subtree (bottom-up)*/
template <typename T>
static void goAlongLeftBranch(BinNodePosi(T) x, Stack <BinNodePosi(T)>& S)
{
while (x) { S.push(x); x = x->lChild; }
}// Repeatedly stack and go deep along the left branch
template <typename T, typename V> void travIn_I1(BinNodePosi(T) x, V& visit) {
Stack <BinNodePosi(T)> S; // Auxiliary stack
while (true) {// Repeatedly
goAlongLeftBranch(x, S); // Starting from the current node, batch by batch into the stack
if (S.empty()) break; // Until all nodes are processed
x = S.pop(); // The left subtree of x is either empty or traversed (equivalent to empty), so it can
visit(x->data); // visit
x = x->rChild; // Then turn to its right subtree
}
}
T= O(n)
G post order traversal (school online)
/* Postorder traversal_ recursion*/
template <typename T, typename VST>
void traverse(BinNodePosi<T> x, VST& visit) {
if (!x) return;
traverse(x->lc, visit);
traverse(x->rc, visit);
visit( x-> data)
}
/* Postorder traversal_ iteration*/
template <typename T> static void gotoLeftmostLeaf(Stack <BinNodePosi<T>>& S) {
while( BinNodePosi<T> x = S.top() ) // Check the top node of stack repeatedly from top to bottom
if (HasLChild(*x)) {// As far left as possible
if (HasRChild(*x)) // If there is a right child, then
S.push(x->rc); // Priority stack
S.push(x->lc); // Then turn to the left child
}
else // It's a last resort
S.push(x->rc); // Just turn to the right child
S.pop(); // Before returning, pop up the empty node at the top of the stack
}
template <typename T, typename VST>
void travPost_I(BinNodePosi<T> x, VST& visit) {
Stack <BinNodePosi<T>> S; // Auxiliary stack
if (x) S.push(x); // The root node is stacked first
while (!S.empty()) {// x is always the current node
if (S.top() != x->parent) // If the top of the stack is not the father of x (but the right brother)
gotoLeftmostLeaf(S); // Find the leftmost leaf in its right subtree (recursion)
x = S.pop(); // Pop up the top of the stack (i.e. after the previous node) to update x
visit(x->data); // Visit immediately
}
}
H-level traversal
P199
/* level traversal */
template <typename T> template <typename VST>
void BinNode<T>::travLevel(VST& visit) {// Binary tree hierarchy traversal
Queue<BinNodePosi(T)> Q; // Introducing auxiliary queue
Q.enqueue(this); // Root node join
while (!Q.empty()) {// Iterate before the queue becomes empty again
BinNodePosi(T) x = Q.dequeue(); // Take out the first node of the team, and then
visit(x->data); // Visit
if (HasLChild(*x)) Q.enqueue(x->lChild); //Left child joins the team
if (HasRChild(*x)) Q.enqueue(x->rChild); // Right child joins the team
}
}
Queue: first in first out
Suddenly no card, began to watch online in the school
I reconstruction
P202
[first order | second order] + middle order
If there is no middle order, it cannot be reconstructed, because the left subtree and right subtree may be empty
J Huffman tree
Code table: protocol
Prefix- Free Code
Avoid excessive depth difference
Large difference in word frequency:
Income = height difference × Frequency difference
Optimize coding strategy:
- The high frequency should be placed as high as possible, and the low frequency should be placed as low as possible (long)
Supplementary notes:
1. Node range of complete binary tree with height H: [2^(h-1)+1
2^(h+1)-1]
2. For each layer, the depth decreases by 1, but the increase of height may be greater than 1, because the height of the node is determined by the higher of its left and right subtrees.
3. Post order traversal: starting from the root node, for each node in the middle, you can go left to left, but not left to right. If there is no way to go left or right, this node is the first visited node in the post order traversal.
4. Let the binary tree have n nodes with a height of h, insert a new node in it, and the number of nodes whose height changes is O(h).
On the path from the newly inserted node to the root node, the height of all nodes (i.e. the ancestors of the new node) may change.
Chapter VI diagram
A
Terminology, implementation, algorithm
undirected edge
Undirected graph: undigraph
digraph
directed edge
(U, v): tail, u, head
Path: a sequence consisting of a series of vertices that are contiguous in turn
Simple path: a path without duplicate nodes
Directed acyclic graph
Euler loop: pass all sides once, and just once
Hamiltonian loop: pass through each vertex once and exactly once
B adjacency matrix
/* Graph template class*/
template <typename Tv, typename Te> class Graph {//Vertex type, edge type
private:
void reset() {//Reset auxiliary information of all vertices and edges
for (int i = 0; i < n; i++) {// vertex
status(i) = UNDISCOVERED; dTime(i) = fTime(i) = -1;
parent(i) = -1; priority(i) = INT_MAX;
for (int j = 0; j < n; j++)// edge
if (exists(i, j)) status(i, j) = UNDETERMINED;
}
}
public: /* ... Vertex operation, edge operation, graph algorithm*/
};
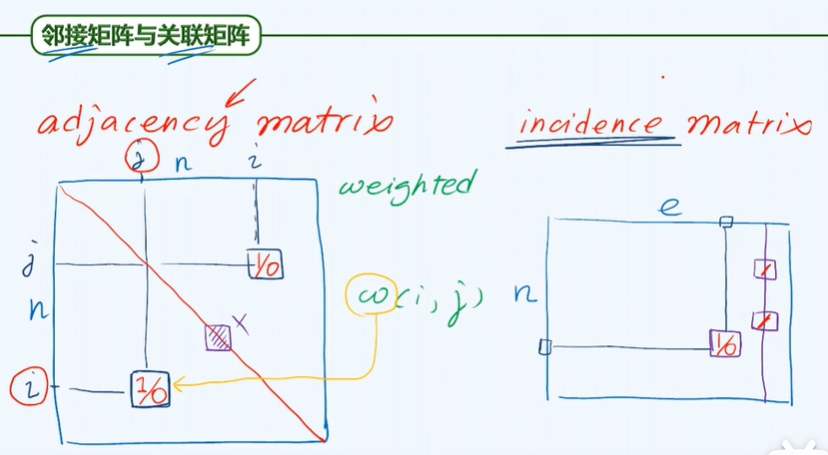
Undirected graph + adjacency matrix: redundancy
/* Vertex */
typedef enum { UNDISCOVERED, DISCOVERED, VISITED}VStatus;
template <typename Tv> struct Vertex {// Vertex object
Tv data; int inDegree, outDegree; // Data and access degree
// For graph traversal
VStatus status; // (above three states)
int dTime, fTime; // Time stamp
int parent; // Parent node in traversal tree
int priority; // Priority in traversal tree (shortest path, very short edge crossing, etc.)
Vertex(Tv const& d) : // Construct new vertex
data(d), inDegree(0), outDegree(0), status(UNDISCOVERED),
dTime(-1), fTime(-1), parent(-1),
priority(INT_MAX) {}
};
/* Edge */
typedef enum { UNDETERMINED, TREE,CROSS, FORWARD, BACKWARD}EStatus;
template <typename Te> struct Edge {// Edge object
Te data; // data
int weight; // weight
EStatus status; // type
Edge(Te const& d, int w) : // Construct new edge
data(d), weight(w), status(UNDETERMINED) {}
};
/* GraphMatrix*/
template <typename Tv, typename Te>class GraphMatrix :public Graph<Tv, Te> {
private:
Vector< Vertex<Tv> > V; // Vertex set
Vector< Vector< Edge<Te>* >> E; // Edge set
public:
/* Operation interface: vertex dependent, edge dependent*/
GraphMatrix() { n = e = 0; }// structure
~GraphMatrix() {// Deconstruction
for (int j = 0; j < n; j++)
for (int k = 0; k < n; k++)
delete E[i][j]; // Clear the edge records of all dynamic applications.
}
};
/* vertex operations */
// For any vertex i, enumerate all its adjacent vertices
int nextNbr(int i, int j) {// If it has been enumerated to neighbor j, move to the next neighbor
while ((-1 < j) && !exists(i, --j)); // Reverse order search, O(n)
return j;
}// Use adjacency table to increase to o (1 + outdegree (I))
int firstNbr(int i) {
return nextNbr(i, n); // n: Hypothetical sentry
}// First neighbor
P214 side operation
/* Side operation */
bool exists(int i, int j) {// Judge whether the edge (i, j) exists
return (0 <= i) && (i < n) && (0 <= j) && (j < n) // i. J comparison of legitimacy
&& E[i][j] != NULL; // Short-circuit evaluation
}
/* Edge insertion */
void insert(Te const& edge, int w, int i, int j) {// Insert (i, j, w)
if (exists(i, j)) return; // Ignore existing edges
E[i][j] = new Edge<Te>(edge, w); // Create new edge
e++; // Update edge count
V[i].outDegree++; // Update the out degree of the associated vertex i
V[j].inDegree++; // Update the penetration of the associated vertex j
}
/* Edge deletion */
Te remove(int i, int j) {// Delete the join edges between vertices i and j (exists(i, j))
Te eBak = edge(i, j); // Backup information of side (i, j)
delete E[i][j]; E[i][j] = NULL; // Delete edges (I, J)
e--; // Update edge count
V[i].outDegree--; // Update the out degree of the associated vertex i
V[j].inDegree--; // Update the penetration of the associated vertex j
return eBak; //Returns the information of the deleted edge
}
/* Introducing new vertices */
int insert(Tv const& vertex) {// Insert vertex, return number
for (int j = 0; j < n; j++)
E[j].insert(NULL); n++;
E.insert( Vector< Edge<Te>*>(n, n, NULL) );
return V.insert(Vertex<Tv>(vertex));
}
/* Vertex deletion */
Tv remove(int i) {// Delete the vertex and its associated edge, and return the vertex information
for(int j=0; j<n; j++)
if (exists(i, j))// Delete all outgoing edges
{
delete E[i][j]; V[j].inDegree--;
}
E.remove(i); n--; // Delete line i
for(int j=0; j<n; j++)
if (exists(j, i))// Delete all edges and column i
{
delete E[j].remove(i); V[j].outDegree--;
}
Tv vBak = vertex(i); // Backup vertex i information
V.remove(i); // Delete vertex i
return vBak; // Returns the information of the deleted vertex
}
Plan graph
Meet: v - e + f - c = 1
Plan: e ≤ 3n-6
D. breath first search
P217
simplify what is complicated
Spanning Tree
Hierarchical traversal of tree
/* Graph: BFS()Breadth first search*//* Breath-First-Search*/
template <typename Tv, typename Te>// Vertex type, edge type
void Graph<Tv, Te>::BFS(int v, int& clock) {
Queue<int> Q; status(v) = DISCOVERED; Q.enqueue(v); //initialization
while ( !Q.empty() ) {// Repeatedly
int v = Q.dequeue();
dTime(v) = ++clock; // Take out the top v of the team and
for (int u = firstNbr(v); -1 < u; u = nextNbr(v, u))//Check every neighbor u of v
/* ... Depending on the state of u, deal with it separately */
status(v) = VISITED; // So far, the current vertex access is completed
}
}
/* Graph: BFS()Breadth first search*//* Breath-First-Search*/
template <typename Tv, typename Te>// Vertex type, edge type
void Graph<Tv, Te>::BFS(int v, int& clock) {
Queue<int> Q; status(v) = DISCOVERED; Q.enqueue(v); //initialization
while ( !Q.empty() ) {// Repeatedly
int v = Q.dequeue();
dTime(v) = ++clock; // Take out the top v of the team and
for (int u = firstNbr(v); -1 < u; u = nextNbr(v, u))//Check every neighbor u of v
/* ... Depending on the state of u, deal with it separately */
status(v) = VISITED; // So far, the current vertex access is completed
}
}
///
while (!Q.empty()) {// Repeatedly
int v = Q.dequeue(); dTime(v) = ++clock; // Take out the top v of the team and
for( int u= firstNbr(v); -1 <u; u=nextNbr(v, u) )// Check every neighbor u of v
if (UNDISCOVERED == status(u)) {// If u has not been found, then
status(u) = DISCOVERED; Q.enqueue(u); // The vertex was found
status(v, u) = TREE; parent(u) = v; // Introduce tree edge
}
else// If u has been found (in the queue), or even accessed (out of the queue), then
status(v, u) = CROSS; // Classify (v, u) as span edge
status(v) = VISITED; // At this point, the current vertex access is completed
}
The continuous, regular and compact organization form is conducive to the role of cache mechanism.
P222 multi connected
/* Multiple connectivity */
/* Graph::bfs() */
template <typename Tv, typename Te>// Vertex type, edge type
void Graph<Tv, Te>::bfs(int s) {// s is the starting point
reset(); int clock = 0; int v = s; // initialization
do // Check all vertices one by one. Once you encounter a vertex that has not been found
if (UNDISCOVERED == status(v)) //
BFS(v, clock); // That is, start BFS once from this vertex
while (s != (v = (++v % n)));
// Access by serial number, so it is not missed or repeated
}
P224 shortest path
E depth first search
P225
Support tree
/* Graph:: DFS() */ /* Depth-First Search , Depth first search */
template Graph<Tv, Te>::DFS(int v, int & clock) {
dTime(v) = ++clock; status(v) = DISCOVERED; // Find current vertex v
for (int u = firstNbr(v); -1 < u; u = nextNbr(v, u)) // Enumerate each neighbor u of v
/* ... Depending on the state of u, deal with it separately */
/* ... Unlike BFS, it contains recursion */
status(v) = VISITED; fTime(v) = ++clock; // At this point, the current vertex v direction access is completed
}
/*****************/
for( int u = FirstNbr(v); -1< u; u = nextNbr(v, u)) // Enumerate all neighbors of v
switch (status(u)) { // And treat them separately according to their status
case UNDISCOVERED: // u has not been found, which means that the support tree can be extended here
status(v, u) = TREE; parent(u) = v; DFS(u, clock); break; // recursion
case DISCOVERED: // u has been discovered but has not been visited. It should belong to the ancestor pointed by future generations
status(v, u) = BACKWARD; break;
default: // If u has been VISITED (VISITED, directed graph), it can be divided into forward edge or cross edge according to the inheritance relationship
status(v, u) = dTime(v) < dTime(u) ? FORWARD : CROSS; break;
}
Backtrack
P229 directed graph
Edge classification
P231 bracket principle / nesting principle
Supplementary notes:
1. The number of TREE edges is always equal to the number of vertices minus the number of connected components.
2. When DFS is performed on the graph, the BACKWARD edge means that the graph contains loops.
School online:
Zero entry algorithm for F1 topological sorting
Topology sorting:
For any directed graph (not necessarily directed acyclic graph (DAG)), try to arrange all vertices into a linear sequence so that the suborder must be compatible with the original graph
- In any directed acyclic graph, there must be a point with zero degree.
/* Topological sorting: output zero degree vertices sequentially */
// Store all vertices with zero degree into stack S and empty queue Q
while (!S.empty()) {
Q.enqueue(v = S.pop()); // Stack top v into queue
for each edge(v, u)// The adjacent vertex of v, if the penetration is only 1
if (u.inDegree < 2) S.push(u); // Then enter the stack
G = G\ { v }; // Delete v and its associated edges (adjacency vertex penetration minus 1)
}
return | G | ? "NOT A DAG" : (? ); // Only if the original graph can be topologically sorted
Zero out degree algorithm for F2 topological sorting
- Begin with the end in mind. (beginning with the end)
- A real farmer doesn't need to be anxious... He doesn't require all the products to belong to him when he completes his work every day. What he offers is not only his first fruit, but also his last fruit.
----From Walden
Supplementary notes
1. In a simple undirected graph with n vertices, the maximum number of edges is: (n-1) × n/2
2. The number of edges of an undirected graph is equal to half of the sum of the degrees of each vertex.
3. A+ D = MM^T: a (adjacency matrix of simple undirected graph G), M (incidence matrix of G), D (diagonal matrix in which the ith element on the diagonal is the degree of vertex i)
4. The space complexity of realizing a graph with n vertices and e edges by adjacency matrix is O(n^2)
5. The time complexity of deleting edge (i, j) is O(1)
6. Time complexity of accessing data stored in vertex v O(1)
Chapter VII application of map (school online)
A1 double connected component: judgment criteria
information cocoons
Joint points (after removal, the number of connected domains increases)
Leaf nodes are not joint points
The highest ancestor
A2 biconnected component decomposition: algorithm
/* Graph:: BCC() */
#Define hca() (fTime (x)) / / use the idle fTime here
template <typename Tv, typename Te>
void Graph<Tv, Te>::BCC(int v, int& clock, Stack<int>& S) {
hca() = dTime(v) = ++clock; status(v) = DISCOVERED; S.push(v);
for (int u = firstNbr(v); -1 < u; u = nextNbr(v, u))
switch (status(u))
{ /* ...Depending on the state of u, deal with it separately*/
case UNDISCOVERED:
parent(u) = v; type(v, u) = TREE; // Expand tree edge
BCC(u, clock, S); // Start traversal from u and return
if (hca(u) < dTime(v))// If u points back to the true ancestor of v
hca(v) = min(hca(v), hca(u)); // Then v the same is true
else // Otherwise, take v as the joint point (below u is a BCC, and the vertices are concentrated at the top of stack S)
while (u != S.pop()); // Pop up all nodes in the current BCC (except v)
// Further treatment as required
break;
case DISCOVERED:
type(v, u) = BACKWARD;
if (u != parent(v))
hca(v) = min(hca(v), dTime(u)); // Update hca[v], smaller higher
break;
default:
type(v, u) = dTime(v) < dTime(u) ? FORWARD : CROSS;
break;
}
status(v) = VISITED; // End of access to v
}
# undef hca
A3 double connected component decomposition: Example
B priority search (BAG)
template <typename Tv, typename Te>
template<typename PU> // Priority updater (function object)
void Graph<Tv, Te>::pfs(int s, PU prioUpdater) {
priority(s) = 0; status(s) = VISITED; parent(s) = -1; // The starting point s is added to the PFS tree
while (1) {// Adds the next vertex and edge to the PFS tree
/* ... Introduce n-1 vertices (and N-1 edges) in turn*/
for (int w = firstNbr(s); -1 < w; w = nextNbr(s, w)) // To s each neighbor w
prioUpdater(this, s, w); // Updates the priority of vertices w and their parent vertices
for( int shortest = INT_MAX, w = 0; w < n; w++)
if( UNDISCOVERED == status(v) ) // From vertices that have not been added to the traversal tree
if (shortest > priority(w)) // Pick the next one
{
shortest = priority(w); s = w;
}// Highest priority vertex s
if (VISITED == status(s)) break; // Until all vertices have been added
status(s) = VISITED; type(parent(s), s) = TREE; // Add s to the traversal tree
}//while
}
C Dijkstra algorithm (shortest path method)
Creating tools
Reduce and govern
/* PrioUpdater() */
g->pfs(0, DijkstraPU<char, int>()); // Starting from vertex 0, start Dijkstra algorithm
template <typename Tv, typename Te>struct DijkPU {// Vertex priority updater of Dijkstra algorithm
virtual void operator() { Graph <Tv, Te>* g, int uk, int v } {//For every uk
if (UNDISCOVERED != g->status(v)) return; // Undiscovered neighbors v, press
if (g->priority(v) > g->priority(uk) + g->weight(uk, v)) {// Dijkstra
g->priority(v) = g->priority(uk) + g->weight(uk, v);
g->parent(v) = uk; // Do relaxation
}
}
};
D Prim algorithm (minimum spanning tree problem)
Minimum tree covering all nodes in the graph: support tree
Weight cannot be negative
After cutting, the weight will not increase
Incremental construction
The minimum spanning tree is not unique (different starting points, different spanning trees)
Find the shortest one first. Isn't this the shortest overall?
/* PrioUpdater()*/
g->pfs(0, PrimPU<char, int>()); // Starting from the vertex, start the Prim algorithm
template <typename Tv, typename Te>struct PrimPU {// Vertex priority updater of Prim algorithm
virtual void operator() (Graph<Tv, Te>* g, int uk, int v) {// For every uk
if (UNDISCOVERED != g->status(v)) return; // Undiscovered neighbors v, press
if (g->priority(v) > g->weight(uk, v)) {// Prim
g->priority(v) = g->weight(uk, v);
g->parent(v) = uk; // Do relaxation
}
}
};
Chapter 8 binary search tree
P232
A
Definition, characteristics and specifications
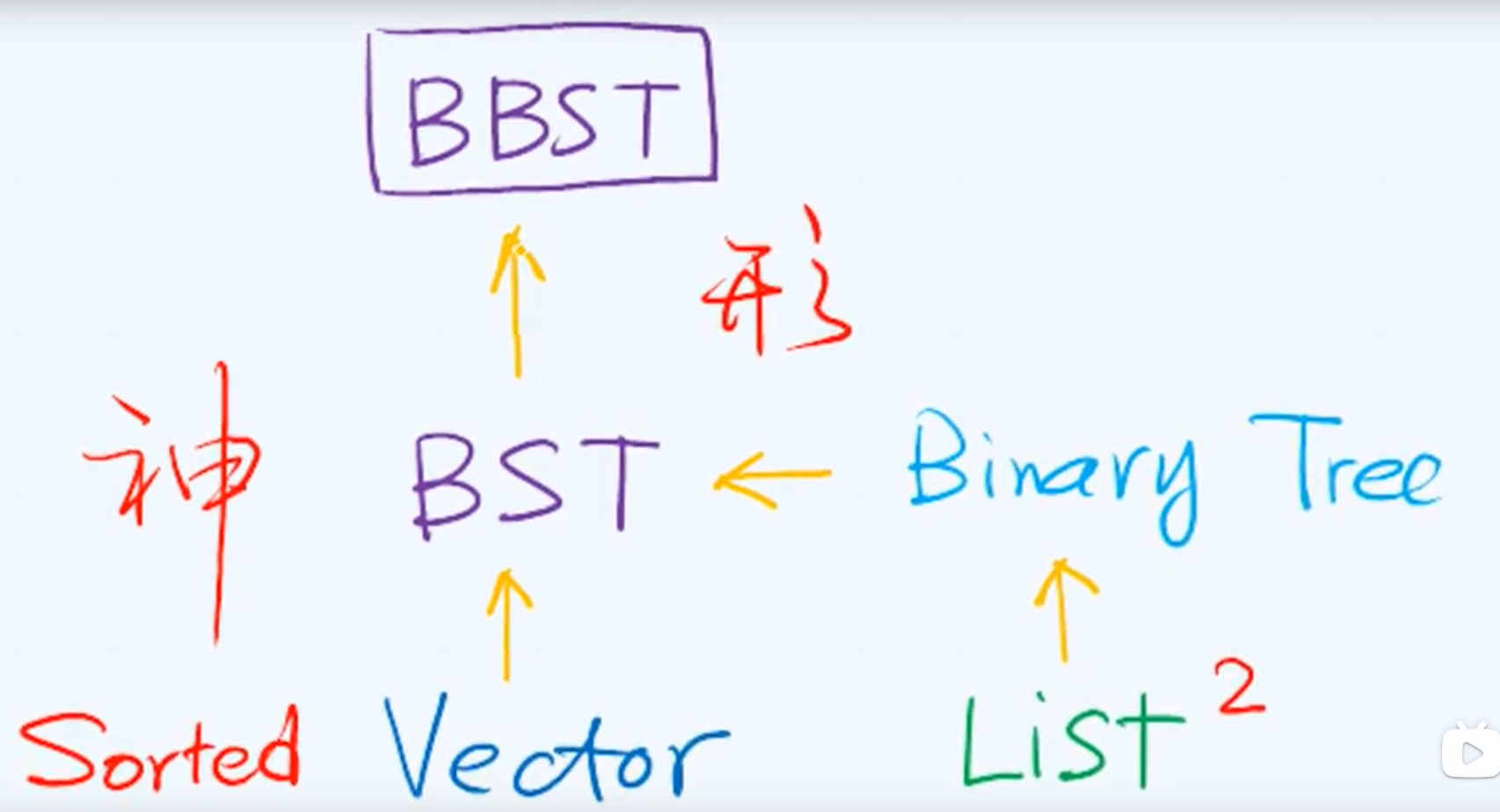call - by - key
Key
Comparison and comparison
entry
/* Entry */
template <typename K, typename V> struct Entry {// Entry template class
K key; V value; // Key and value
Entry(K k = K(), V v = V())::key(k), value(v) {}; // Default constructor
Entry(Entry<K, V> const& e)::key(e.key), value(e.value) {}; // clone
// Comparator, discriminator
bool operator< (Entry<K, V> const& e) { return key < e.key; } //less than
bool operator> (Entry<K, V> const& e) { return key > e.key; } // greater than
bool operator == (Entry <K, V> const& e) { return key == e.key; } // be equal to
bool operator != (Entry <K, V> const& e) { return key != e.key; } // Not equal to
};
Node ~ entry ~ key
The middle order ergodic sequence of BST must be monotonic and non descending
/* BST template class */
template <typename T> class BST : public BinTree<T> {// Derived from BinTree
public: // Decorated with virtual to override derived classes
virtual BinNodePosi(T)& search(const T&); // lookup
virtual BinNodePosi(T) insert(const T&); // insert
virtual bool remove(const T&); // delete
protected:
BinNodePosi(T) _hot; // Father of hit node
BinNodePosi(T) connect34(// 3 + 4 reconstruction
BinNodePosi(T), BinNodePosi(T), BinNodePosi(T),
BinNodePosi(T), BinNodePosi(T), BinNOdePosi(T), BinNOdePosi(T));
BinNodePosi(T) rotateAt(BinNodePosi(T)); // Rotation adjustment
};
B1 BST: find
P237
Reduce and govern
/* Binary search tree: finding*/
template <typename T> BinNodePosi(T)& BST<T>::search(const T& e)
{
return searchIn(_root, e, _hot = NULL); // Start lookup from root node
}
static BinNodePosi(T)& searchIn(// Typical tail recursion can be changed to daddy's version
BinNodePosi(T)& v, // Current (sub) tree root
const T& e, // Target key
BinNodePosi(T)& hot)// Memory hotspot
{
if (!v || (e == v->data)) return v; // Sufficient to determine success or failure, success, or
hot = v; // First write down the current (non empty node), and then
return searchIn(((e < e->data) ? v->lChild : v->rChild), e, hot);
}// The running time is proportional to the depth of the return node v, which does not exceed the tree height O(h)
Add sentinel node
B2 BST: Insert
P242
/* Binary search trees: inserting*/
template <typename T> BinNodePosi(T) BST<T>::insert(const T& e) {
BinNodePosi(T)& x = search(e); // Find target
if (!x) {// Similar elements are prohibited, so the insertion operation is implemented only when the search fails
x = new BinNode<T>(e, _hot); // Create a new node at x to_ hot for father
_size++; updateHeightAbove(x); // Update the size of the whole tree, update x and the height of its ancestors
}
return x; // Whether e exists in the original tree or not, there is always X - > data = = E
}
B3 BST: delete
/* Binary search tree: deleting */
template <typename T> bool BST<T>::remove(const T& e) {
BinNodePosi(T)& x = search(e); // Locate the target node
if (!x) return false; // Confirm that the target exists (at this time _hot is the father of x)
// The element cannot be deleted until it exists
removeAt(x, _hot); // Delete and update the size of the whole tree in two categories
_size--; // Update full tree size
updateHeightAbove(_ hot); // Renew_ hot and the height of its ancestors
return true;
}// Whether the deletion is successful or not is indicated by the return value
/* Binary search tree deletion*/
/* Case 1: if a subtree of * x is empty, it can be replaced by another subtree */
template <typename T> static BinNodePosi(T)
removeAt(BinNodePosi(T)& x, BinNodePosi(T)& hot) {
BinNodePosi(T) w = x; // The initial value of the node actually removed is the same as x
BinNodePosi(T) succ = NULL; // The successor of the actually deleted node
if (!HasLChild(*x)) succ = x = x->rChild; // Left subtree is empty
else if (!HasRChild(*x)) succ = x = x->lChild; // The right subtree is empty
else { /* ... The coexistence of left and right subtrees*/ // Situation 2
w = w->succ(); swap(x->data, w->data); // Make * x exchange data with its successor
BinNodePosi(T) u = w->parent; // The original problem is transformed into removing the non quadratic node w
(u == x ? u->rChild : u->lChild) = succ = w->rChild;
}
hot = w->parent; // Record the parent of the node actually deleted
if (succ) succ->parent = hot; // Associate the successor of the deleted node with hot
release(w->data); release(w); // Release the removed node
return succ; // Return to successor
}// O(1)
/* Case 2: */
/*1,Find the minimum point in the right subtree and exchange it to the node to be deleted,
* 2,At this time, you can continue to process the node to be deleted according to the first situation
*/
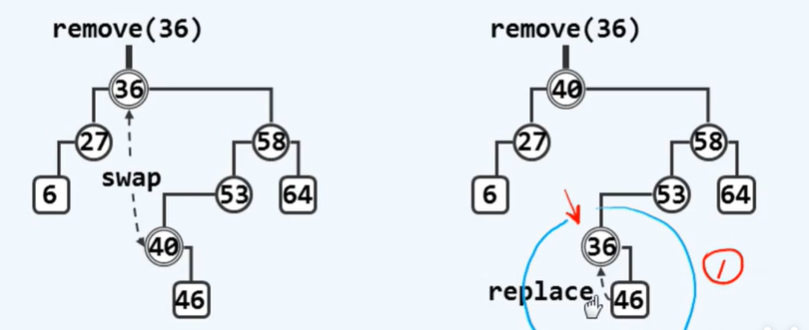
C balance
P248
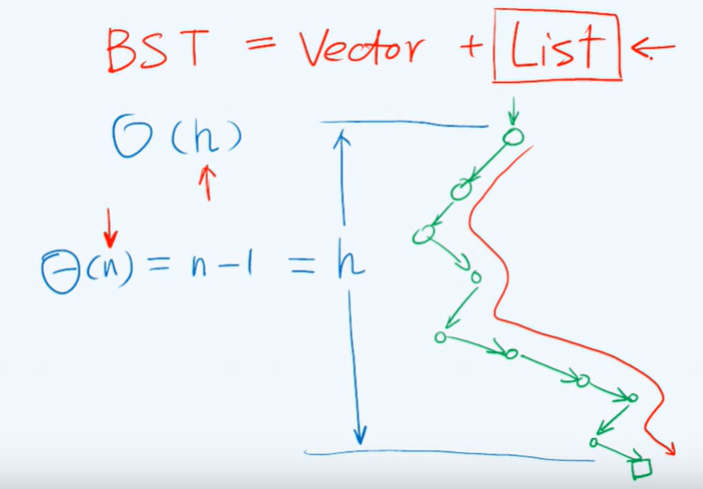
Random generation: O(logn)
Random composition: O(n^0.5), more reliable
Ideal balance:
Moderate balance: if it does not exceed O(logn) gradually, it can be called moderate balance.
Moderately balanced BST: balanced binary search tree (BBST)
Middle order ergodic ambiguity
Equivalent BST: variable up and down, no disorder left and right
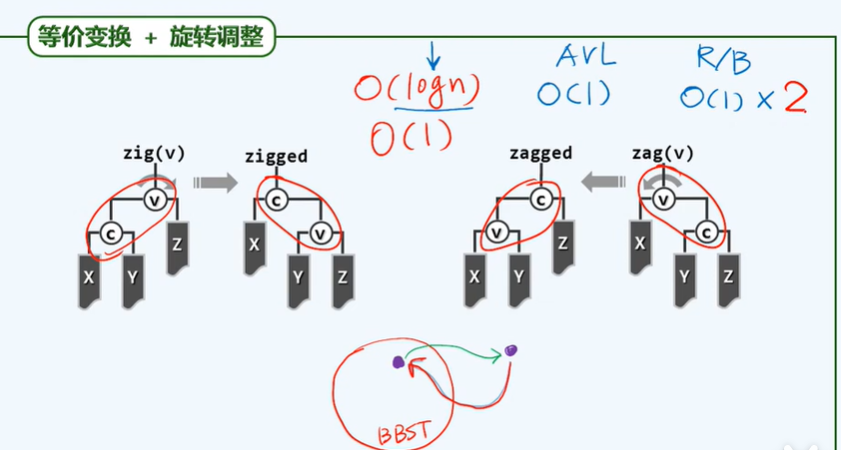
D1 & 2 AVL tree: rebalance
P253
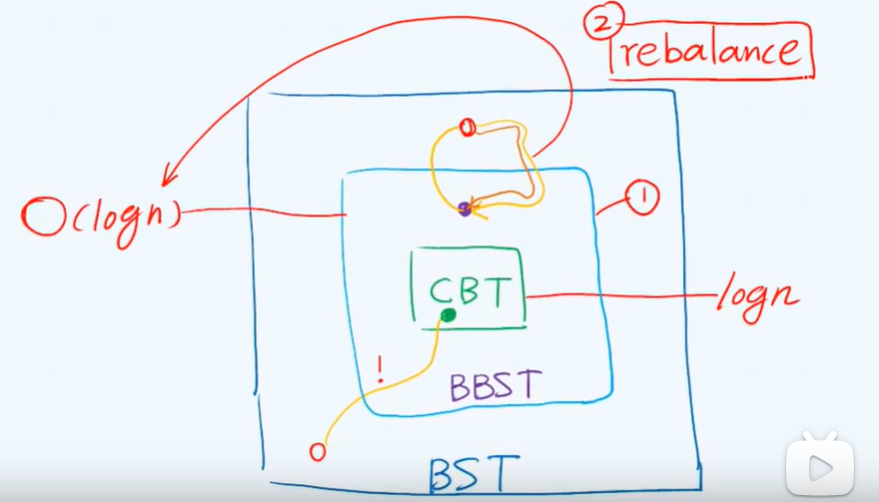
Balance factor = left subtree height - right subtree height
AVL tree = moderately balanced
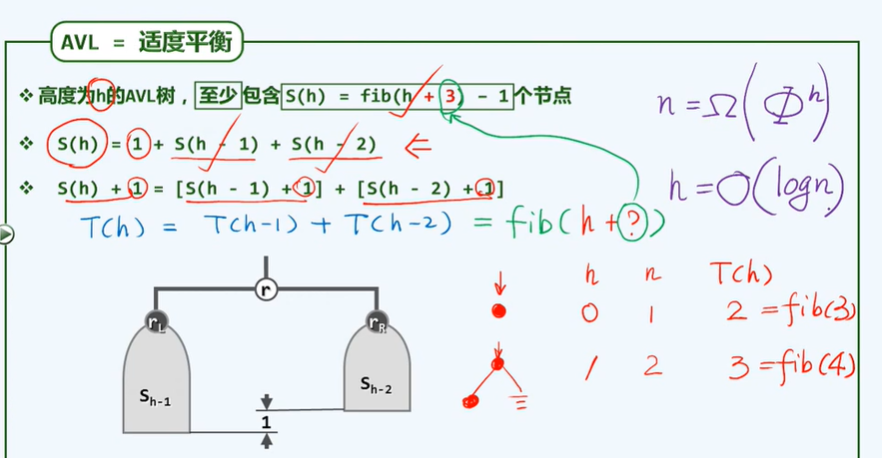
/* AVL Interface */
#define Balanced(x) \ / / ideal balance
( stature ( (x).lChild ) == stature( (x).rChild ) )
#define BalFac(x) \ / / balance factor
( stature( (x).lChild ) - stature ( (x).rChild ) )
#Define avlbalanced (x) \ / / AVL balance condition
( ( -2 < BalFac(x) ) && ( BalFac(x) < 2 ) )
template <typename T> class AVL :public BST<T> {// Derived from BST
public: // BST::search() and other interfaces can be used directly
BinNodePosi(T) insert(const T&); // Insert override
bool remove(cosnt T&); // Delete override
};
Notes:
- After inserting a node into the AVL tree, the maximum number of unbalanced nodes is O(lgn)
- After deleting a node in the AVL tree, the maximum number of unbalanced nodes is O(1)
D3 AVL tree: inserting
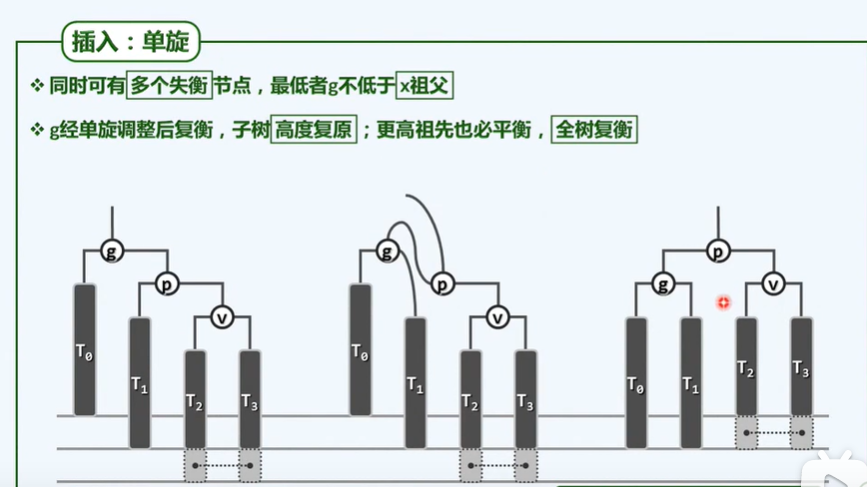
zagzag
zigzig
O(1)
zigzag
zagzig
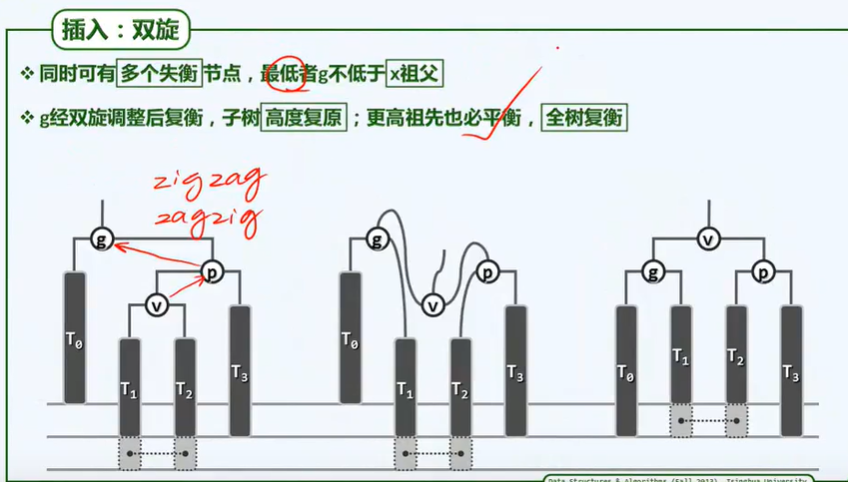
/* AVL Trees: inserting*/
template <typename T> BinNodePosi(T) AVL<T>::insert(const T& e) {
BinNodePosi(T)& x = search(e); if (x) return x; // If the target does not exist
x = new BinNode<T>(e, _hot); _size++; BinNodePosi(T) xx = x; // Create x
// Starting from the father of x, check the ancestors g of each generation layer by layer
for( BinNodePosi(T) g = x-> parent; g; g= g->parent)
if (!AvlBalanced(*g)) {// Once g imbalance is found, the balance is restored by adjustment
FromParentIn(*g) = rotateAt( tallerChild( tallerChild(g) ) );
break; // g after rebalancing, the height of local subtree must be restored; Their ancestors must be the same, so the adjustment is over
}
else // Otherwise (before the group that is still balanced)
updateHeight(g); // Update its height
return xx; // Return to new node: only one adjustment is required at most
}
D4AVL tree: deleting
P261
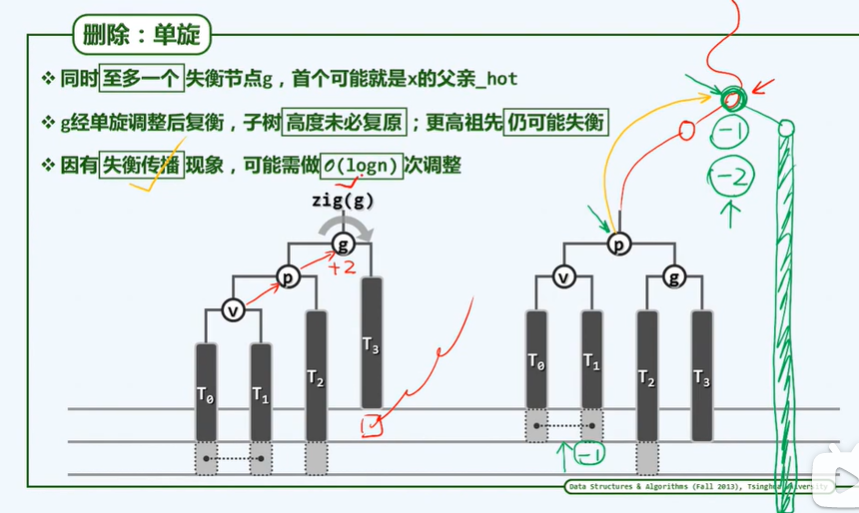
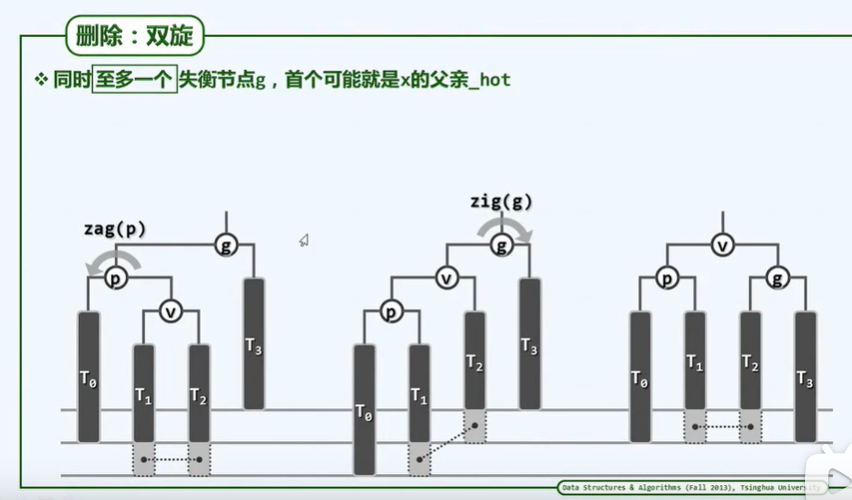
/* AVL Trees: deleting */
template <typename T> bool AVL<T>::remove(const T& e) {
BinNodePosi(T)& x = search(e); if (!x) return false; // If the target does exist
removeAt(x, _hot); _size--; // After deleting according to BST rules_ Both hot and ancestors may be unbalanced
// From_ Starting from hot, check the ancestors of each generation layer by layer
for (BinNodePosi(T) g = _hot; g; g = g->parent) {
if ( !AvlBalanced(*g) ) // Once g imbalance is found, the balance is restored by adjustment
g = FromParentTo(*g) = rotateAt( tallerChild( tallerChild(g) ) );
updateHeight(g); // Update height
}
return true; // Deleted successfully
}
The deletion of nodes in AVL tree causes imbalance, which is rebalanced after rotation adjustment. At this time, the height of subtree containing g, P and V may remain unchanged or decrease by 1.
Correcting the imbalance caused by deleting nodes in AVL tree may lead to imbalance propagation
Correcting the imbalance caused by inserting nodes in AVL tree will not cause imbalance propagation
D5 AVL tree: 3 + 4 reconstruction
P264
Rubik's cube assembly
Middle order traversal
/* 3 + 4 restructure */
template <typename T> BinNodePosi(T) BST<T>::connect34(
BinNodePosi(T) a, BinNodePosi(T) b, BinNodePosi(T) c,
BinNodePosi(T) T0, BinNodePosi(T) T1, BinNodePosi(T) T2, BinNodePosi(T) T3)
{
a->lChild = T0; if (T0) T0->parent = a;
a->rChild = T1; if (T1) T1->parent = a; updateHeight(a);
c->lChild = T2; if (T2) T2->parent = c;
c->rChild = T3; if (T3) T3->parent = c; updateHeight(c);
b->lChild = a; a->parent = b;
b->rChild = c; c->parent = b; updateHeight(b);
return b; // The new root node of the subtree
}
template<typename T> BinNodePosi(T) BST<T>::rotateAt(BinNodePosi(T) v) {
BinNodePosi(T) p = v->parent, g = p->parent; // Father, grandfather
if (isLChild(*p))// zig
if (IsLChild(*v)) {// Zig Zig (both V and P are left children)
p->parent = g->parent;// Upward connection
return connect34(v, p, g,
v->lChild, v->rChild, p->rChild, g->rChild);
}
else {// Zig zag (P is the left child, v is the right subtree)
v->parent = g->parent; //Upward connection
return connect34(p, v, g,
p->lChild, v->lChild, v->rChild, g->rChild);
}
else { /* ..zag-zig & zag-zag ..*/}
}
The height and number of nodes of the binary search tree satisfy h = O(n), and the worst time complexity of searching on it is O(n);
n and h of the balanced binary search tree satisfy the relationship h = O(lgn), and the worst time complexity of searching on it is O(lgn).
Chapter 10 advanced search tree
P268
Extended tree locality
A1 stretch tree: stretch layer by layer
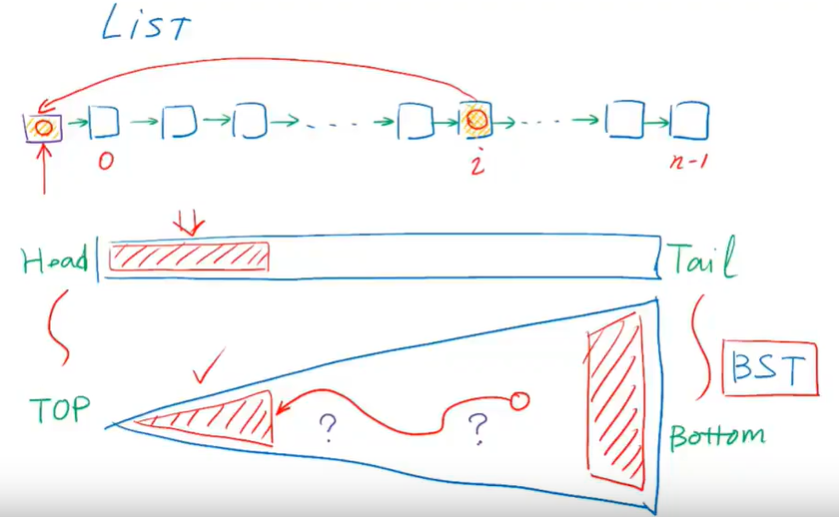
Transfer the newly visited node to the tree root
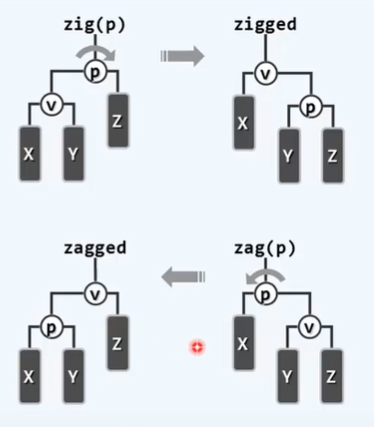
Climb up step by step: single rotation layer by layer
A2 stretch tree: double layer stretch
Go up two layers, not one
Repeatedly examine the three generations of ancestors and grandchildren
Rotate twice and rise two layers
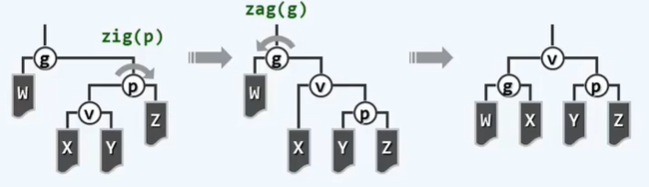
For Zig zig and zag zag
Layer by layer:
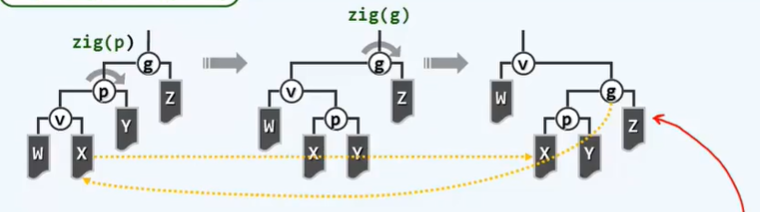
double-deck
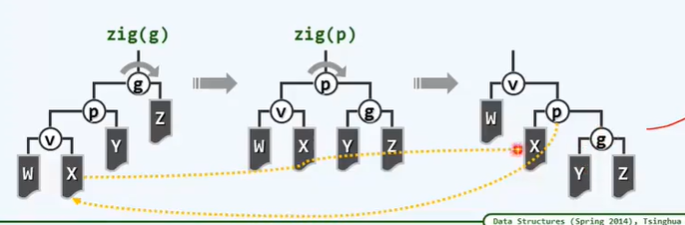
After the double-layer extension, the tree height is reduced to half of the original
Path folding
Allocation O(logn)
A3 extended tree: algorithm implementation
P282
/* Extended tree interface */
template <typename T>
class Splay : public BST<T> {// Derived from BST
protected: BinNodePosi(T) splay(BinNodePosi(T) v); // Extend v to the root
public:
BinNodePosi(T)& search(const T& e); // lookup
BinNodePosi(T) insert(const T& e); // insert
bool remove(const T& e); // delete
};
/* Stretch algorithm */
template <typename T> BinNodePosi(T) Splay<T>::splay(BinNodePosi(T) v) {
if (!v) return NULL; BinNodePosi(T) p; BinNodePosi(T) g; // Father, grandfather
while ((p = v->parent) && (g = p->parent)) {// From bottom to top, repeated double-layer stretching
BinNodePosi(T) gg = g->parent; // After each round. v will be fathered by his great grandfather
if( IsLChild( * v))
if (IsLChild(*p)) { /* zig-zig*/ }
else {/*zig-zag*/}
else if (IsRChild(*p)) {/*zag-zag*/ }
else {/*zag-zig*/}
if (!gg) v->parent = NULL; // If there is no great grandfather gg, v is now the root of the tree; Otherwise, after that, v should be left or right
else(g == gg->lc) ? attachAsLChild(gg, v) : attachAsRChild(gg, v); // children
updateHeight(g); updateHeight(gg, v); updateHeight(v);
}// At the end of double-layer stretching, there must be g==NULL, but p may not be empty
if (p = v->parent) {/*If p is really a root, it only needs another single spin (at least one more time)*/ }
v->parent = NULL; return v; // Stretch out and v reach the root of the tree
}
if (IsLChild(*v)) {
if (IsLChild(*p)) {// zig-zig
attachAsLChild(g, p->rc);
attachAsLChild(p, v->rc);
attachAsRChild(p, g);
attachAsRChild(v, p);
}else { /* zig-zag*/}
}
else {
if (IsRChild(*p)) { /* zag-zag */}
else { /* zag-zig*/}
}
/* lookup */
template <typename T> BinNodePosi(T)& Splay<T>::search(const T& e) {
// Call the internal interface of the standard BST to locate the target node
BinNodePosi(T) p = searchIn(_root, e, _hot = NULL);
// Whether successful or not, the last visited node will extend to the root
_root = splay(p ? p : _hot); // Success, failure
// Always return the root node
return _root;
}
Locality
Insert:
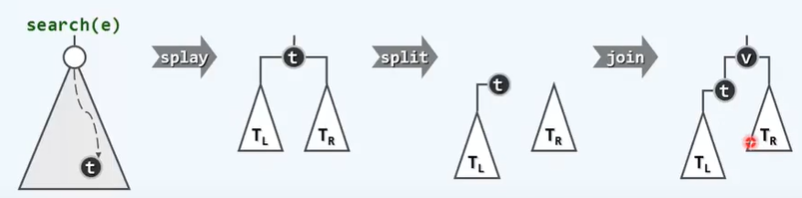
Delete:
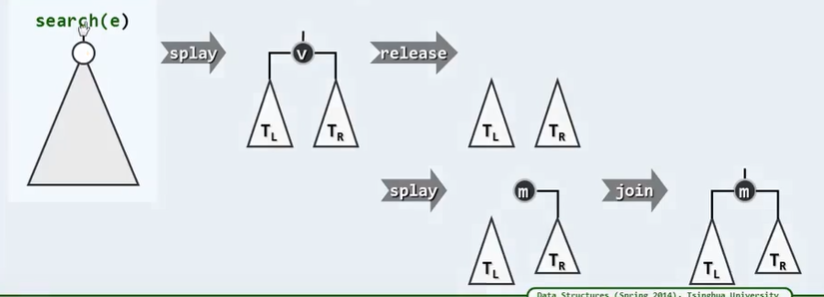
Comprehensive evaluation:
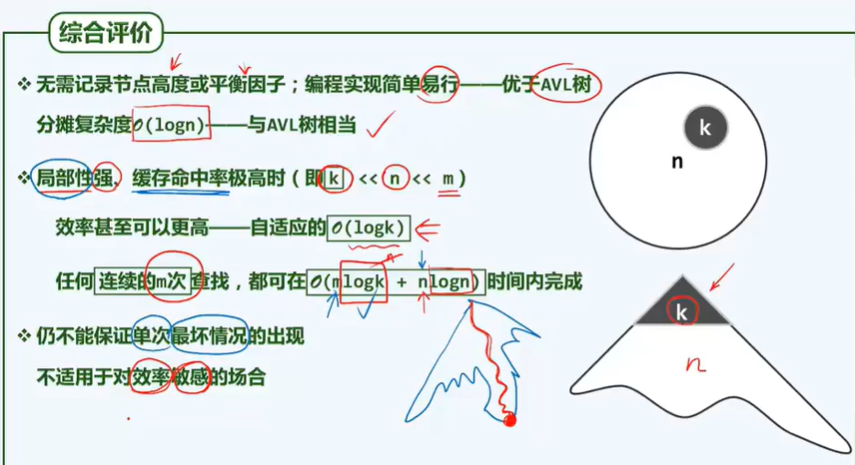
B1 B-tree: big data
P289
Achieve efficient I/O
640k ought to be enough for anybody.
—B.Gates, 1981
Cache
Batch access
B2 B-tree: structure
P295
Wider, shorter
Balanced multiple search tree
P297
2-4 red black trees
Nodes: vectors, sequences
/* BTNode*/
template <typename T> struct BTNode {// B-tree node
BTNodePosi(T) parent; // father
Vector<T> key; // Numerical vector
Vector < BTNodePosi(T) > child; // Child vector (its length is always 1 more than key)
BTNode() { parent = NULL; child.insert(0, NULL); }
BTNode(T e, BTNodePosi(T) lc = NULL, BTNodePosi(T) rc = NULL) {
parent = NULL; // As the root node, and initially
key.insert(0, e); // Only one key, and
child.insert(0, lc); child.insert(1, rc); // Two children
if (lc) lc->parent = this; if (rc) rc->parent = this;
}
};
/* Two vectors */
/* BT tree*/
#Define btnodeposi (T) btnode < T > * / / B-tree node location
template <typename T> class BTree {// B-Trees
protected:
int _size; int _order; BTNodePosi(T) _root; // Total number, order and root of keys
BTNodePosi(T) _hot; // search() the last non empty node accessed (auxiliary dynamic operation)
void solveOverflow( BTNodePosi(T) ); // Split processing after overflow due to insertion
void solveUnderflow( BTNodePosi(T) ); // Consolidation after overflow due to deletion
public:
BTNodePosi(T) search(const T & e); // lookup
bool insert(const T& e); // insert
bool remove(const T& e); // delete
};
Fewer layers of B-tree help reduce the number of I/O
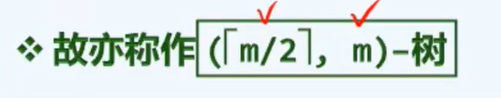
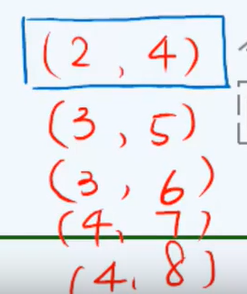
B3 B-trees: finding
P303
One read I/O operation
One time sequential search
The failed search must terminate at the external node
/* lookup */
template <typename T> BTNodePosi(T) BTree<T>::search(const T& e) {
BTNodePosi(T) v = _root; _hot = NULL; // Starting from the root node
while (v) {// Find layer by layer
Rank r = v->key.search(e); // Search in sequence in the vector corresponding to the current node
if (0 <= r && e == v->key[r]) return v; // If successful, return; otherwise
_hot = v; v = v->child[r + 1]; // Go along the reference to the corresponding lower subtree and load its root I/O
}//Ruoyin! v and exit, it means reaching the external node
return NULL; // fail
}
Height of tree h
N success cases, N+1 failure cases.
B4 B-tree: inserting
P309
/* insert */
template <typename T>
bool BTree<T>::insert(const T& e) {
BTNodePosi(T) v = serach(e);
if (v) return false; // Confirm that e does not exist
Rank r = _hot->key.search(e); // Determine the insertion position in node - hot
_hot->key.insert(r + 1, e); // Insert the key into the corresponding position
_hot->child.insert(r + 2, NULL); // Create a null pointer
_size++; solveOverflow(_hot); // If overflow occurs, it needs to be split
return true; // Insert successful
}
T= O(h)
B5 B-trees: deleting
P315
/* delete */
template <typename T>
bool BTree<T>::remove(const T& e) {
BTNodePosi(T) v = search( e );
if ( ! v ) return false; // Confirm e exists
Rank r = v->key.search(e); // Confirm the rank of e in v
if (v->child[0]) {// If v not leaves
BTNodePosi(T) u = v->child[r + 1]; // Go straight to the left in the right subtree
while (u->child[0]) u = u->child[0]; // Find the successor of e (must belong to a leaf node)
v->key[r] = u->key[0]; v = u; r = 0; // And exchange positions with it
}// So far, v must be at the bottom, and the r key is the one to be deleted
v->key.remove( r ); v->child.remove( r + 1 ); _size--;
solveUnderflow(v); return true; // Rotate or merge if necessary
}
If you look left and right and cannot rotate, consider merging
The reduction of B-tree height only occurs when two children of the root node merge.
1. The time spent in the insert operation mainly comes from search(e)
- In the B-tree, the time cost of cross node access (I/O operation) is much greater than that of sequential access within the node
2. The time spent in the deletion operation mainly comes from the time spent in search(e) and searching for subsequent nodes. The subsequent search needs to be cross node. Deleting is more time-consuming
In the worst case, the two costs are equal.
C1 red black tree: motivation
P319
Version number
Consistency structure / persistence
P321 relevance
Share a lot and update a little
P322
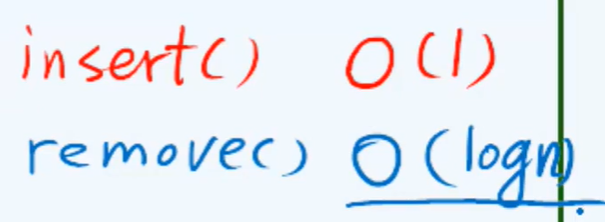
C2 red black tree: structure
P323
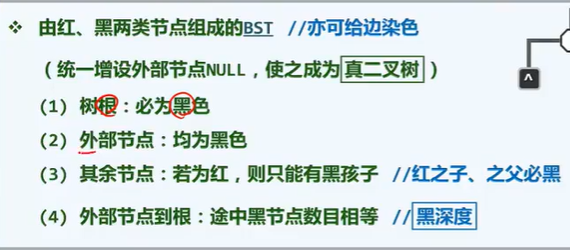
Red black tree is a special case of BBST
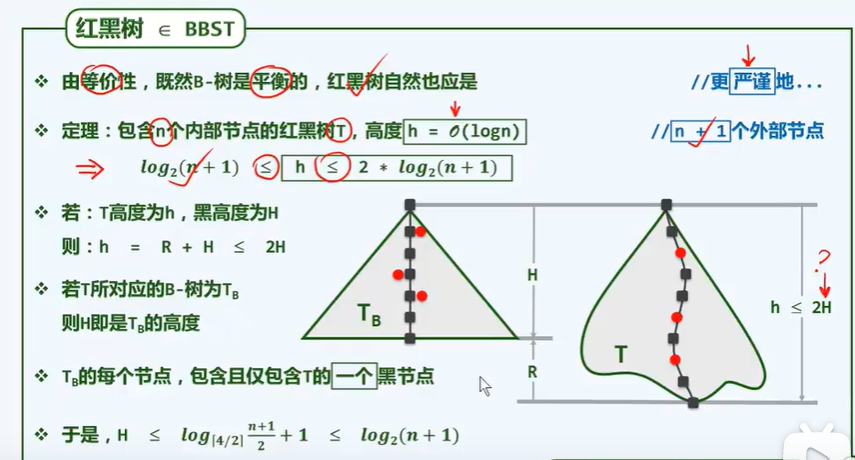
/* Red black tree interface definition */
template <typename T> class RedBlack : public BST<T> {//Red black tree
public: // BST::search() and other interfaces can be used directly
BinNodePosi(T) insert(const T& e); // insert
bool remove(const T& e); // delete
protected:
void solveDoubleRed(BinNodePosi(T) x); // Double red correction
void solveDoubleBlack(BinNodePosi(T) x); // Double black correction
int updateHeight(BinNodePosi(T) x); // Update the height of node x, black height
};
template <typename T> int RedBlack<T>::updateHeight(BinNodePosi(T) x) {
x->height = max(stature(x->lc), stature(x->rc));
if (IsBlack(x)) x->height++; return x->height; // Count only black nodes
}
C3 red black tree: Insert
P330
/* Treatment of double red defect */
template <typename T> BinNodePosi(T) RedBlack<T>::insert(const T& e) {
// Confirm that the target node does not exist
BinNodePosi(T)& x = serach(e); if (x) return x;
// Create a red node x to_ hot as father, black height - 1
x = new BinNode<T>(e, _hot, NULL, -1); _size++;
// If necessary, double red correction is required
solveDoubleRed(x);
// Returns the inserted node
return x ? x : _hot->parent;
}// Whether e exists in the original tree or not, there is always X - > data = = e when returning
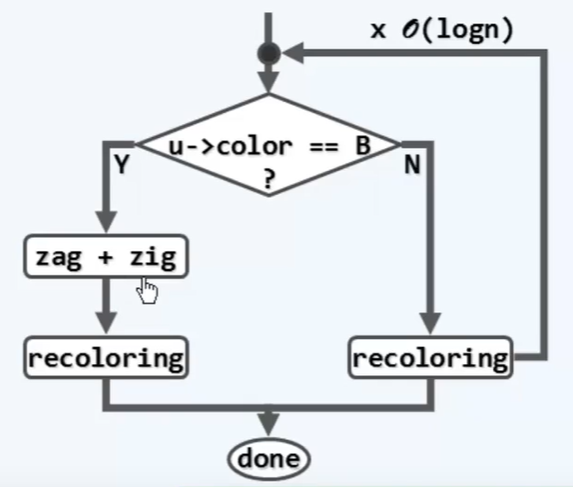
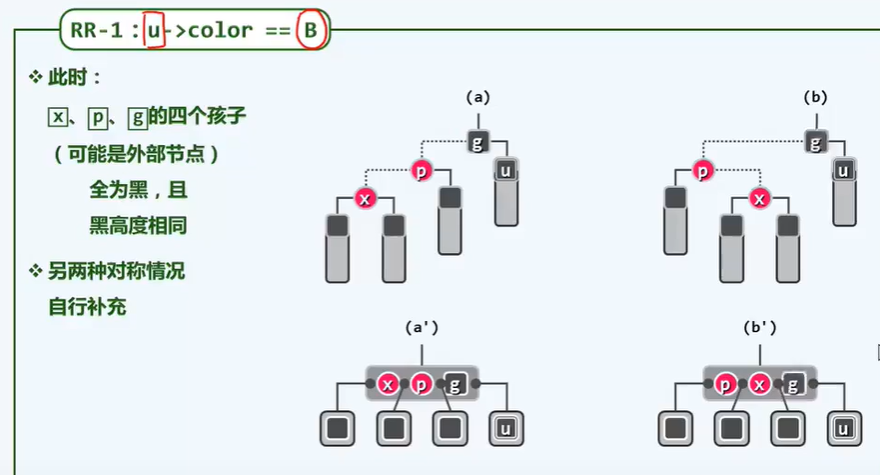
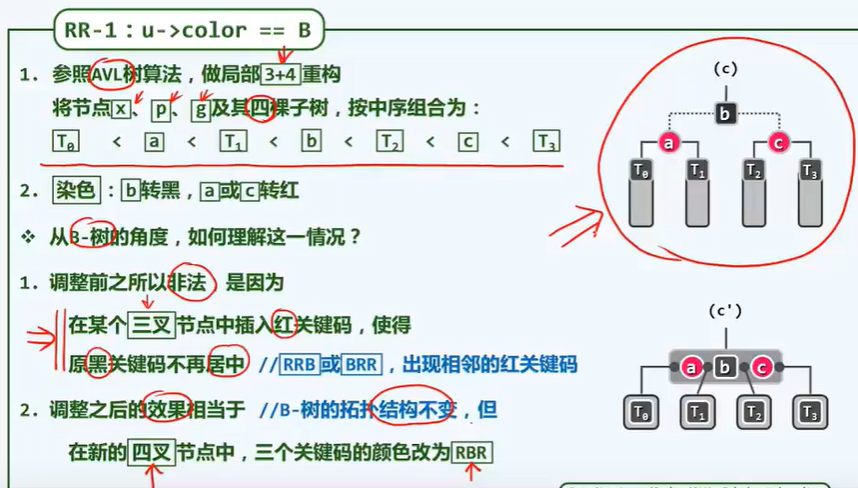
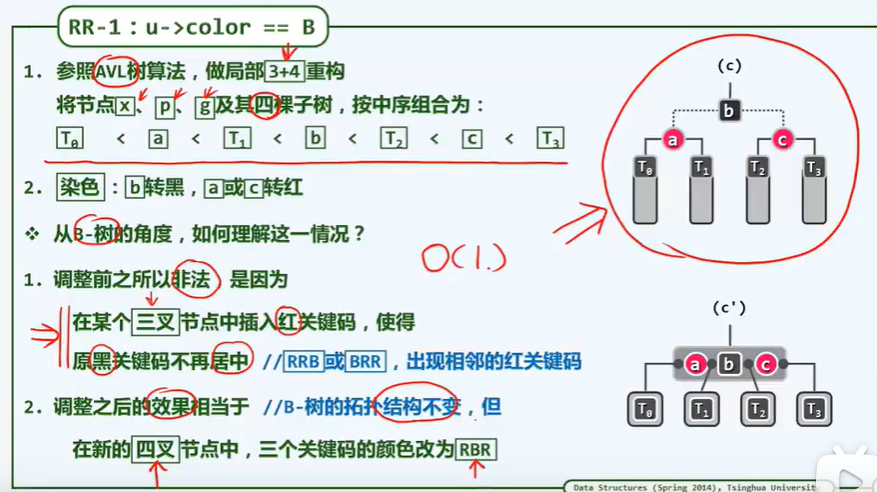
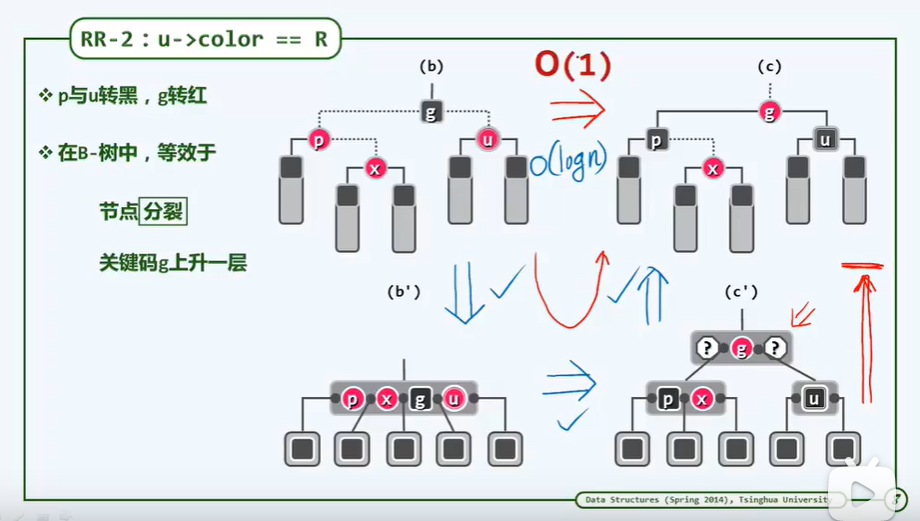
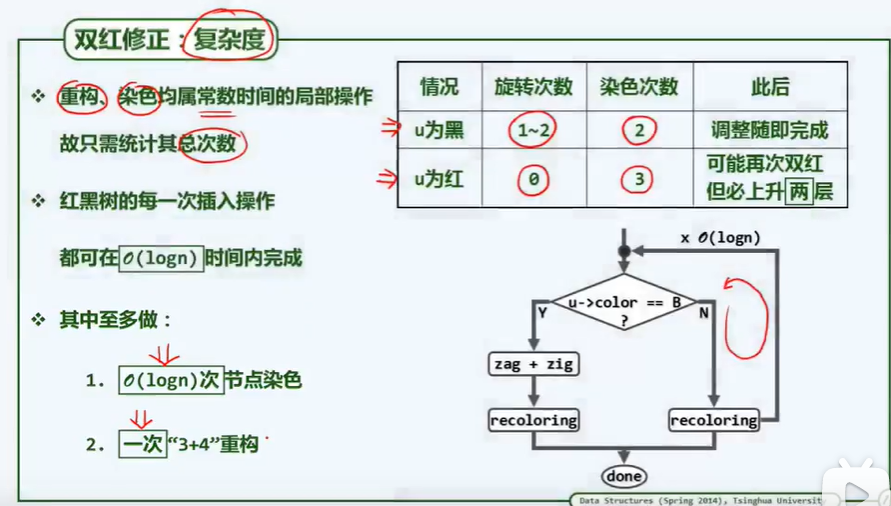
C4 red black tree: delete
Double Black: the deleted points are black, resulting in the number of black nodes on some paths being reduced by 1
BB-1
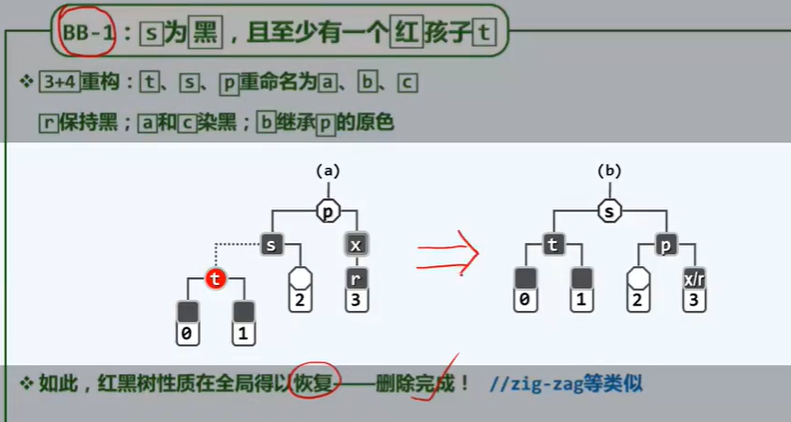
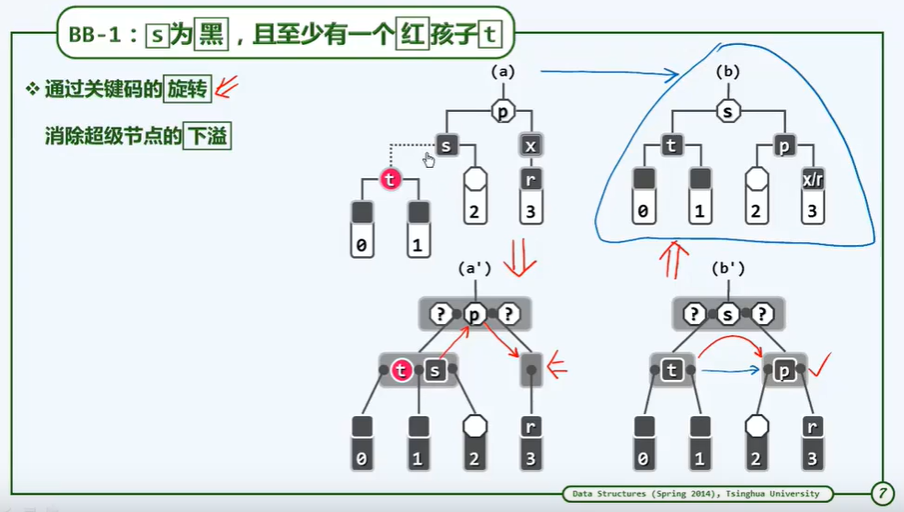
BB- 2B
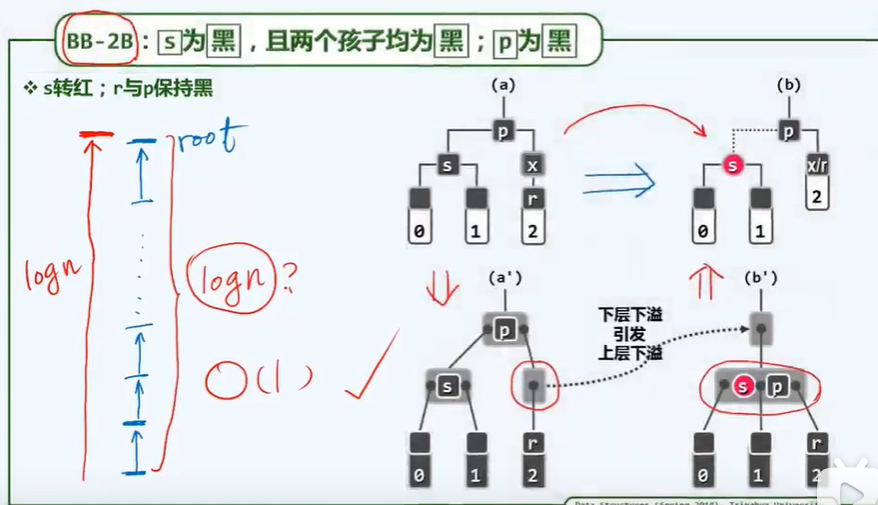
BB- 3
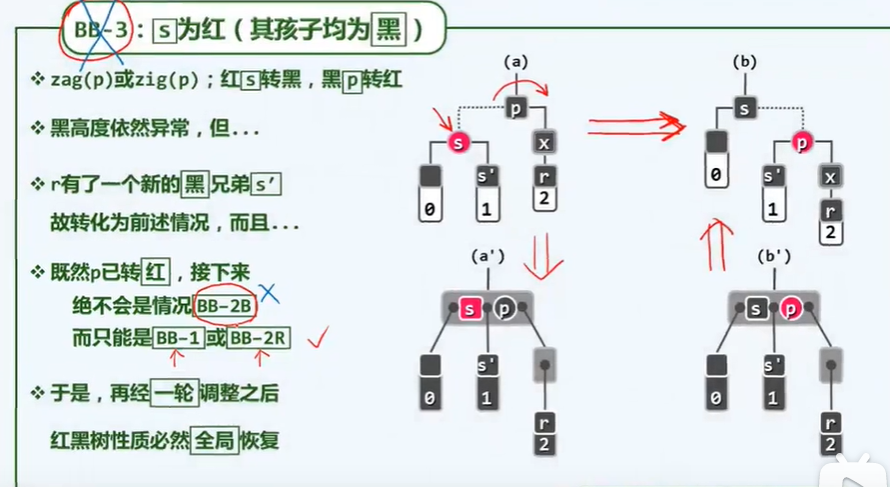
summary
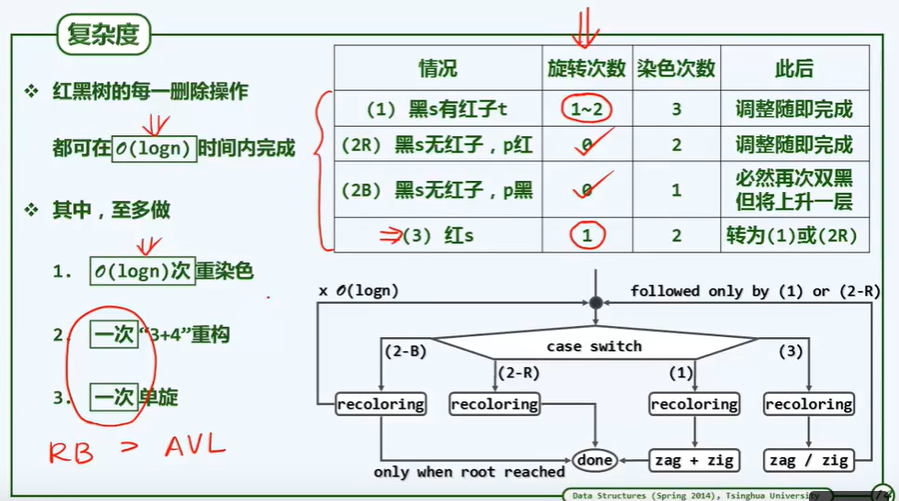
Supplementary notes
1. The worst-case time complexity of a single lookup operation of an extended tree is greater than that of an AVL tree
2,
Access of large-scale data (not all stored in memory): B-tree
It is easy to implement, and the allocation complexity of each interface is O(lgn): extended tree
Dealing with geometry related problems: kd tree
After expansion, it can support access to historical versions: red black tree
P11 dictionary
P345
A hash
Service telephone
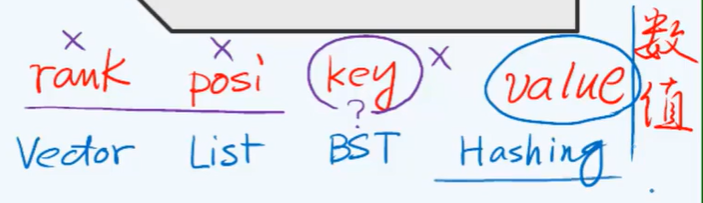
Hashing: translation hash
Bucket: bucket
Bucket array bucket array / hash table
B hash function
P351
Hash function:
1. OK: the same key is always mapped to the same address
2. Fast
3. Full shot
4. Uniform and avoid aggregation
1. Residual method
- hash(key) = key % M
- When M is a prime number, the data covers the hash table most fully and distributes most evenly
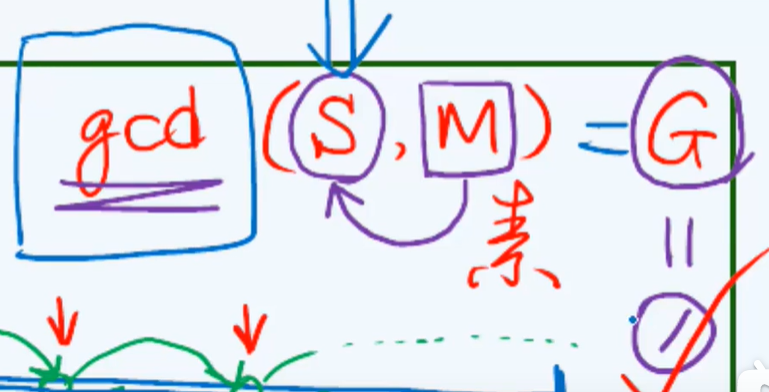
Defects of residual method:
- Fixed point: always have hash(0) = 0
- Zero order uniform: [0,R) keys are evenly distributed to M buckets; however, the hash addresses of adjacent keys must also be adjacent
First order uniformity: adjacent keys, hash addresses are no longer adjacent
2. MAD method
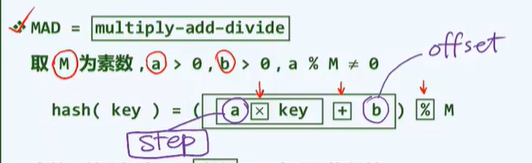
3. Digital analysis
4. Square median
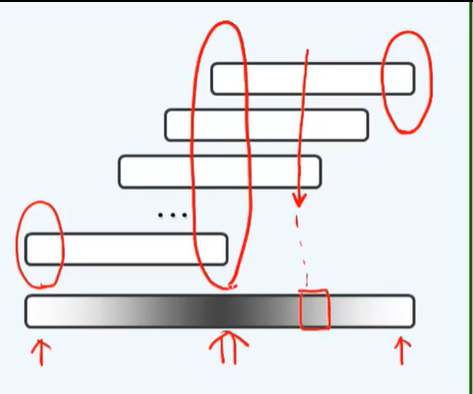
Reason for taking the middle number: the middle number is accumulated by more digits
5. Folding method
6. Exclusive or method
- The implementation of pseudo-random number generator will be different due to different platforms, and the portability is poor
P359
/* Polynomial method: applicable to English strings */
static size_t hashCode(char s[]) {//Approximate polynomial
int h = 0;
for (size_t n = strlen(s), i = 0; i < n; i++) {
h = (h << 5) | (h >> 27);
h += (int)s[i];
}
return (size_t) h;
}
C conflict resolution (1) (2)
P362
Dynamic maintenance, hash conflict is inevitable
1. Multi slot position
2. Independent chain
open addressing / closed hashing
3. Linear probing: in case of conflict, probe the adjacent bucket unit
lazy removal: only the deletion mark is made, and the search chain does not need to be continued
Insufficient linear test: the test distance is too close
4. Square probing
- It can alleviate the aggregation phenomenon
5. Bidirectional square test
M prime = 4k + 3
Double square theorem (Fermat): any prime number p can be expressed as the sum of squares of a pair of integers if and only if p% 4 = 1
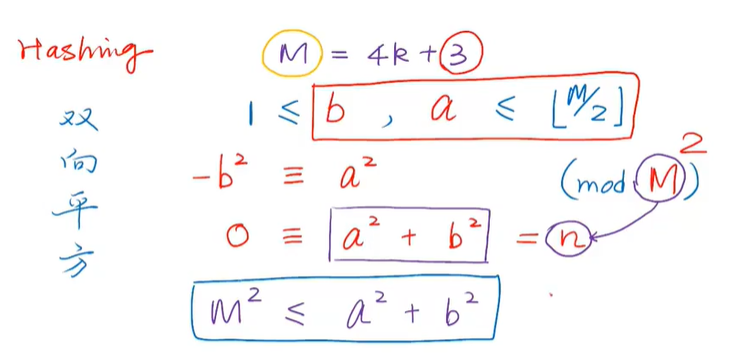
D-bucket sorting
P375
distribution
F count sort
P377
The value range of N elements to be sorted is [1,M], and the time complexity of counting sorting is O(M+N)
Supplementary notes:
1. Using open addressing to resolve conflicts, the actual position of the entry is not necessarily the corresponding hash function value
Chapter 12 priority queue
P378
A1 needs and motivations
Night clinic
Multitask scheduling
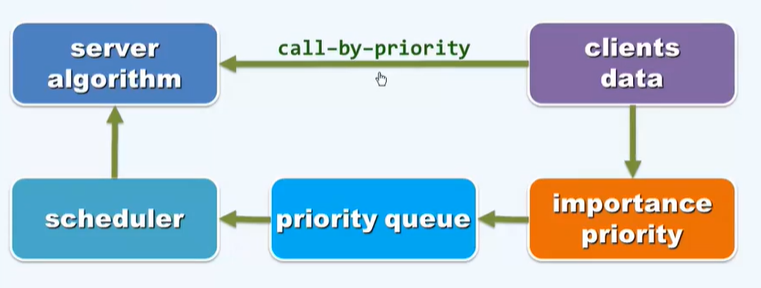
Priority based access
/* Priority queue */
template <typename T> struct PQ { // priority queue
virtual void insert(T) = 0; // Insert entries in order of priority
virtual T getMax() = 0; //Take out the entry with the highest priority
virtual T delMax() = 0; // Delete the entry with the highest priority
};// Priority queue: abstract data type
A2 basic implementation
P381
Balance cost and efficiency
Vector:
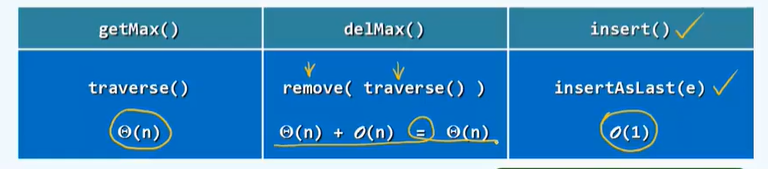
Sorted Vector
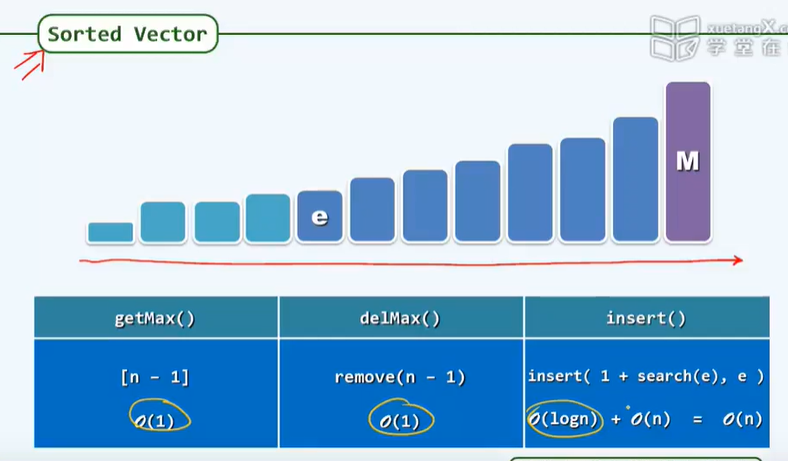
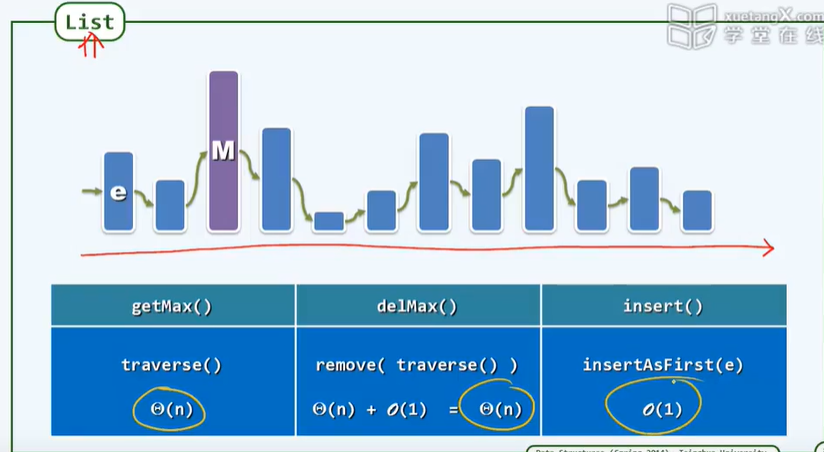
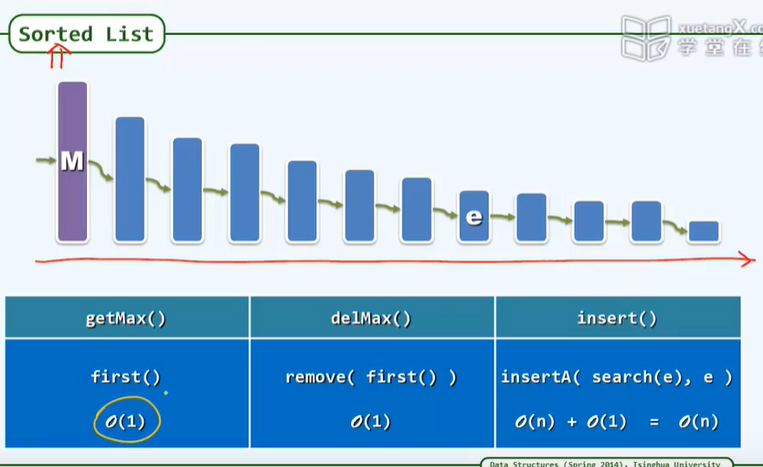
Extreme element, partial order
B1 complete binary reactor: structure
P384
complete Binary Tree: AVL with non negative balance factor everywhere
Logically, it is equivalent to a complete binary tree
Physically, it is realized directly with the help of vectors
Complete Binary Tree
#define Parent(i) ( (i-1) >> 1) # Define lchild (I) (1 + ((I) < 1)) / / odd #Define rchild (I) ((1 + (I)) < 1) / / even
multiple inheritance
/* PQ_ComplHeap = PQ + Vector*/
template <typename T> class PQ_ComlHeap : public PQ<T>, public Vector<T> {
protected: Rank percolateDown(Rank n, Rank i); // Lower filtration
Rank percolateUp(Rank i); // Upper filtration
void heapify(Rank n); // Floyd heap building algorithm
public:
PQ_ComplHeap(T* A, Rank n)// Batch construction
{
copyFrom(A, 0, n); heapiffy(n);
}
void insert(T); // Insert entries according to the priority determined by the comparator
T getMax() { return _elem[0]; } // Read the entry with the highest priority
T delMax(); // Delete the entry with the highest priority
};
Heap ordering
/* H[0] That is, the global maximum element */
template <typename T> T
PQ_ComplHeap<T>::getMax() { return _elem[0]; }
B2 complete binary reactor: insert and percolate up
P388
Insert entry e: take e as the last element to access the vector (which may destroy heap ordering), and then filter up
/* Heap insert */
template <typename T> void PQ_ComplHeap<T>::insert(T e)// insert
{
Vector<T> ::insert(e); percolateUp(_size - 1);
}
template <typename T>// Filter up the ith entry, i <_ size
Rank PQ_ComplHeap<T>::percolateUp(Rank i) {
while ( ParentValid(i) ) { // As long as i there is a father (who has not yet reached the top of the pile), then
Rank j = Parent(i); // Record the father of i as j
if (lt(_elem[i], _elem[j])) break; // Once the father and son are no longer in reverse order, the upper filtering is completed
swap(_elem[i], _elem[j]); i = j; // Otherwise, swap parent-child positions and go up one level
}// while
return i; // Return to the final position reached by the upper filter
}
h = O(logn)
swap: 3 exchanges.
Improvement: first back up e, determine the location, and then make an exchange
B3 complete binary stack: deletion and downward filtering
P392
Structure and stacking order
The last element is replaced and then filtered down
/* Heaps: deleting*/
template <typename T> T PQ_ComplHeap<T>::delMax() {// delete
T maxElem = _elem[0]; _elem[0] = _elem[--_size]; // Remove the top of the pile and replace it with the last entry
percolateDown(_size, 0); // Perform down filtration on the new reactor top
return maxElem; // Returns the maximum entries previously backed up
}
template <typename T>// Filter down the ith of the first n entries, i < n
Rank PQ_ComplHeap<T>::percolateDown(Rank n, Rank i) {
Rank j; // father
while (i != (j = ProperParent(_elem, n, i))) // As long as i is not j, then
{
swap(_elem[i], _elem[j]); i = j; // Transposition and continue to investigate i
}
return i; // Return to the position reached by the lower filter
}
Efficiency:
compare
Swap 3logn
B4 complete binary reactor: batch reactor construction
P396
Heapification
1. Top down top filtration
/* Top down top filtration */
PQ_ComplHeap(T* A, Rank n) { coptFrom(A, 0, n); heapify(n); }
template <typename T> void PQ_ComplHeap<T>::heapify(Rank n) {
for (int i = 1, i < n; i++) // When traversing a node according to the hierarchy, there is no need to filter up, so start from 1
percolateUp(i); // Insert each node through upper filter
}
T(n) = nlogn
2. Bottom up filtering
Partial order
Merge small piles into large piles
delMax()
template <typename T>
void PQ_ComplHeap<T>::heapify(Rank n) {//
for (int i = LastInternal(n); i >= 0; i--) // From bottom to top, from right to left, in turn
percolateDown(n, i); // Filter down internal nodes
} // Layer by layer merging of sub heaps
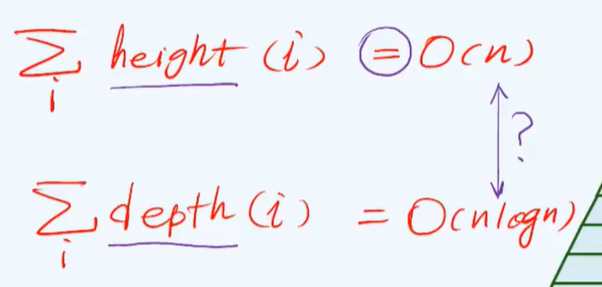
The closer to the bottom layer, the more nodes (brute force method)
C heap sort
P401
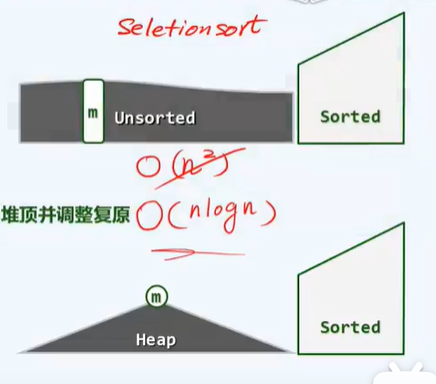
Local O(1)
Exchange + lower filtration
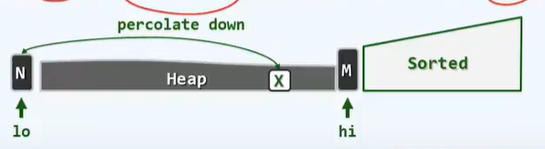
/* Heap sort */
template <typename T> // Sort vectors [lo,hi) in place
void Vector<T>::heapSort(Rank lo, Rank hi) {
PQ_ComplHeap<T> H(_elem + lo, hi - lo); // Heap building in the interval to be sorted, O(n)
while (!H.empty()) // Repeatedly remove the largest element and put it into the sorted suffix until the heap is empty
_elem[--hi] = H.delMax(); // Equivalent to the lower filtration after the exchange between the top and the end elements
}
Heap sorting: continuously call delMax() after creating a heap
F1 & 2 left stack: structure
P405
In order to effectively complete heap merging
Null node path length Null Path Length
- Introduce all external nodes: eliminate the one degree node and turn it into a true binary tree
Height of node
F3 left heap: merge algorithm
P411
/* LeftHeap */
template <typename T> // Based on binary tree, the priority queue is implemented in the form of left heap
class PQ_LeftHeap : public PQ<T>, punlic BinTree<T> {
public:
void insert(T); // Insert elements (in the order of priority determined by the comparator)
T getMax() { return _root->data; } // Take out the element with the highest priority
T delMax(); // Delete the element with the highest priority
};
template <typename T>
static BinNodePosi(T) merge(BinNodePosi(T), BinNodePosi(T));
The left heap does not meet the structural requirements, and the physical structure is no longer compact. It can be derived from the tree structure
/* Left heap: merging*/
template <typename T>
static BinNodePosi(T) merge(BinNodePosi(T) a, BinNodePosi(T) b) {
if (!a) return b; // Recursive basis
if (!b) return a; // Recursive basis
if (lt(a->data, b->data)) swap(b, a); // General situation: first, make sure that b is not large and a is large
a->rc = merge(a->rc, b); // Merge the right sub heap of a with b
a->rc->parent = a; // Update parent-child relationship
if (!a->lc || a->lc->npl < a->rc->npl) // If necessary
swap(a->lc, a->rc); // Swap the left and right sub heaps of a to ensure that the npl of the right sub heap is not large
a->npl = a->rc ? a->rc->npl + 1 : 1; // Update npl of a
return a; // Returns the merged heap top
}
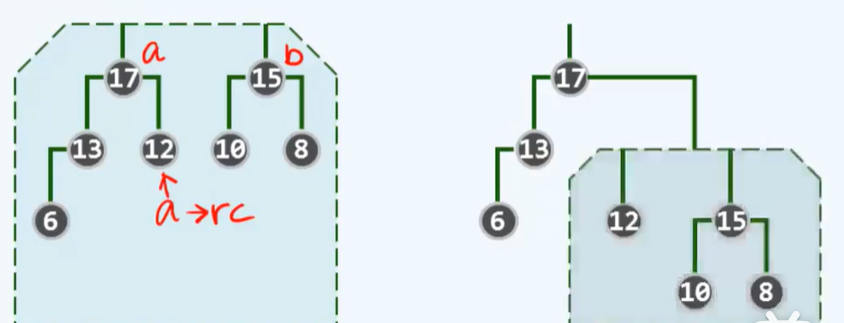
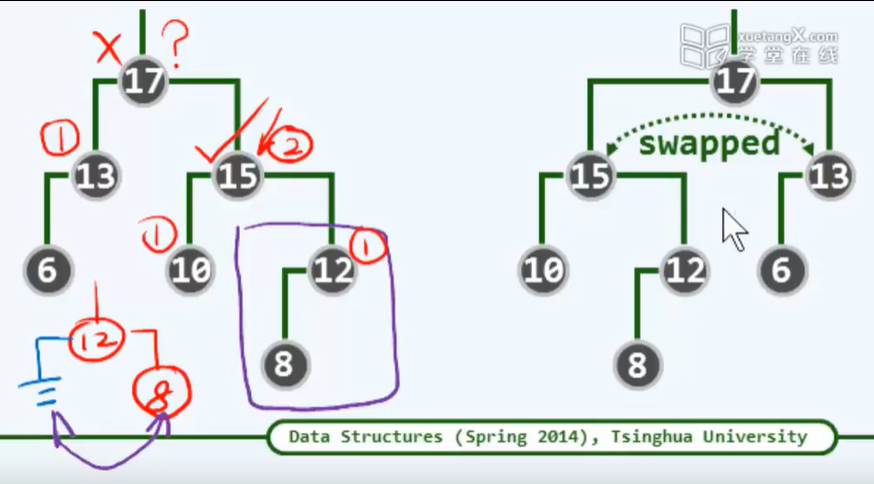
F4 left heap: insert + delete
P415
Insert is merge
/* insert*/
template <typename T>
void PQ_LeftHeap<T>::insert(T e) { // O(logn)
BinNodePosi(T) v = new BinNode<T>(e); // Create a binary tree node for e
_root = merge(_root, v); // The insertion of new nodes is completed by merging
_root->parent = NULL; //
_size++; //Renewal scale
}
Delete:
/* delMax() */
template <typename T> T PQ_LeftHeap<T>::delMax() {// O(logn)
BinNodePosi(T) lHeap = _root->lc; // Zuo zidui
BinNodePosi(T) rHeap = _root->rc; // Right sub heap
T e = _root->data; // Maximum element at the top of the backup heap
delete _root; _size--; // Delete root node
_root = merge(lHeap, rHeap); // Merge the original left and right sub heaps
if (_root) _root->parent = NULL; // Update parent-child connections
return e; // Returns the data item of the original root node
}
Supplementary notes
1. The insert, getmax and delmax interfaces of priority queue realized by balanced binary search tree can achieve the time complexity of O(lgn).
Chapter XIII string
P417
A. ADT
The string is structurally equivalent to a Vector vector
B. Pattern matching
String matching
Text string T, n; Mode string P, m
1. Brute force matching
Move the mode string from left to right in character
/* Brute force matching: Version 1*/
int match(char* P, char* T) {
size_t n = strlen(T), i = 0;
size_t m = strlen(P), j = 0;
while( j < m && i < n)//Match characters one by one from left to right
if (T[i] == T[j]) { i++; j++; } // If it matches, go to the next pair of characters
else { i -= j - 1; j = 0; } // Otherwise, T fallback and P reset
return i - j;
}
/* Brute force matching: version 2*/
int match(char* P, char* T) {
size_t n = strlen(T), i = 0; // Align T[i] with P[0]
size_t m = strlen(P), j; // T[i+j] aligned with P[j]
for (i = 0; i < n - m + 1; i++) { // T from the i th character
for (j = 0; j < m; j++)// Corresponding characters in P
if (T[i + j] != P[j]) break; //In case of mismatch, P moves one character to the right as a whole and compares again
if (m <= j) break; // Matching string found
}
return i;
}
Best case: O(m)
Worst case: O(n) × m)
C1. KMP algorithm: memory method
P426
Worst O(n)
The reason for the inefficiency of brute force method: after T fallback and P reset, the previously compared characters will participate in the comparison again.
？ According to the P-scan T, the mark can match, and then judge. How about it
C2. KMP algorithm: query table
P430
Make adequate plans
/* KMP Main algorithm */ /* Modified on the basis of version 1 of brute force method*/
int match(char* P, char* T) {
int* next = buildNext(p); // Construct next table
int n = (int)strlen(T), i = 0; // Text string pointer
int m = (int)strlen(P), j = 0; // Mode string pointer
while( j < m && i < n)// Compare characters one by one from left to right
if (0 > j || T[i] == P[j]) {// If match
i++; j++; // Hand in hand
}
else// Otherwise, P moves to the right and T does not retreat
j = next[j];
delete[] next; // Release next table
return i - j;
}
C3. KMP algorithm: next [] table
P433
Self matching = fast shift right
Longest self matching = fast shift right + avoid fallback
Next[0] = -1, sentry
Virtual experiment
C4. KMP algorithm: construct next [] table
P436
Recurrence
next[j]: in P[0,j), the length of the maximum self matching true prefix and true suffix.
Self similarity of prefix
/* next[]surface*/
int* buildNext(char* P) {// Construct the netx [] table of pattern string P to match the pattern string itself
size_t m = strlen(P), j = 0; // Main string pointer
int* N = new int(m); // next table
int t = N[0] = -1; // Mode string pointer (P[-1] wildcard)
while (j < m - 1)
if (0 > t || P[j] == P[t]) // matching
N[++j] = ++t;
else // Mismatch
t = N[t];
return N;
}
C5. KMP algorithm: Allocation Analysis
P439
O(n)
For text strings with length N and pattern strings with length m, the time complexity of KMP algorithm is O(m + n)
C6. KMP algorithm: further improvement
P441
court defeat by fighting against overwhelming odds
next query table control program process
/* next Table: improved version*/
int* buildNext(char* P) {
size_t m = strlen(P), j = 0; // Main string pointer
int* N = new int[m]; // next table
int t = N[0] = -1; // Mode string pointer
while( j < m-1)
if (0 > t || P[j] == P[t]) {//matching
j++; t++; N[j] = P[j] != P[t] ? t : N[t];
}
else// Mismatch
t = N[t];
return N;
}
Binary string: KMP
D. BM_BC algorithm
D1. BM_BC algorithm: start with the end
P446
Bad character strategy
Focus on failed comparisons
Let greater failures be exposed earlier
D2. BM_BC algorithm: bad characters
P450
Choose one to avoid backtracking
sentry
D3. BM_BC algorithm: construct bc []
P452
/* Construction bc[] table */
int* buildBC(char* P) {
int* bc = new int[256]; // bc [] table, longer than the alphabet
for (size_t j = 0; j < 256; j++) bc[j] = -1; //Initialization (uniformly pointing to wildcards)
for (size_t m = strlen(P), j = 0; j < m; j++)// Scan from left to right
bc[P[j]] = j; //Refresh the occurrence position record of P[j] (painter algorithm: later overwrite the past)
return bc;
}// The second loop avoids calling strlen() repeatedly by referring to the temporary variable m
D4. BM_BC algorithm: Performance Analysis
P454
Best case O(n/m)
Worst case scenario
O(n×m)
E: BM_GS algorithm
P455
good-suffix
Experience = matching suffix
Among all prefixes P[0,t), take the longest one matching the suffix of U
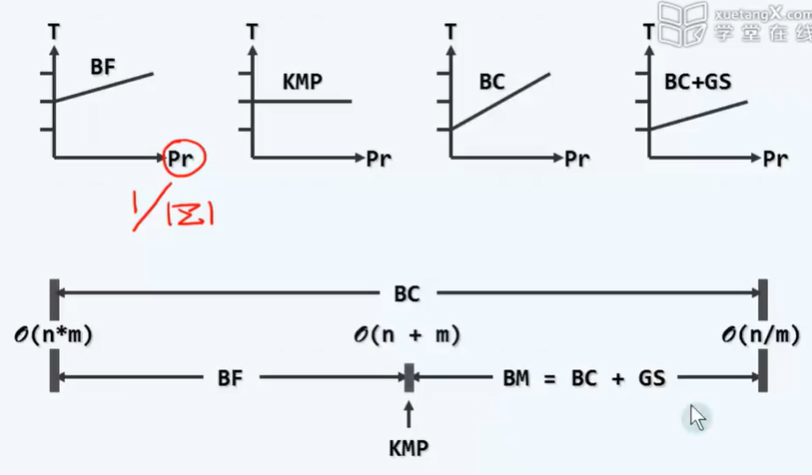
F: Karp Rabin algorithm
P461
A string is an integer
Everything counts
Hash
Modular complementary function
Exclude in O(1) time
Supplementary notes:
1. The return values of brute force string matching method when matching is successful / failed are: the first position of P in T / a number greater than n-m
P14 sorting
P468
Quick sort
divide and rule
Quick sort: the process of converting all elements to pivot points one by one.
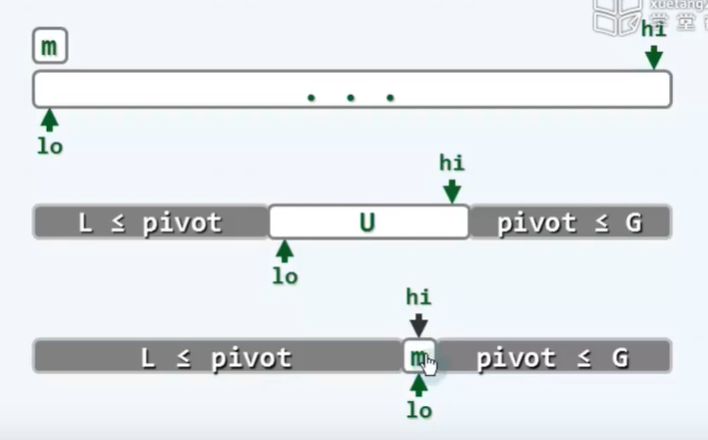
instable
Local
Average performance
a4: quick sort variant
P476
/* Quick sort */
template <typename T> void Vector<T>::quickSort(Rank lo, Rank hi) {
if (hi - lo < 2) return; // Single element intervals are naturally ordered, otherwise
Rank mi = partition(lo, hi - 1); // Construct pivot point first
quickSort(lo, mi); // Prefix sorting
quickSort(mi + 1, hi); // Suffix sorting
}
template <typename T> Rank Vector<T>::partition(Rank lo, Rank hi) { //[lo, hi]
swap(_elem[lo], elem[lo + rand() % (hi - lo + 1)]); // Random exchange
T pivot = _elem[lo]; int mi = lo;
for (int k = lo + 1; k <= hi; k++)// Examine each [k] from left to right
if (_lem[k] < pivot) // If [k] is less than the axis point, then
swap(_elem[++mi], _elem[k]); // Swap with [mi], L extends to the right
swap(_elem[lo], _elem[mi]); // Candidate pivot point homing
return mi; // Returns the rank of the pivot point
}
instable
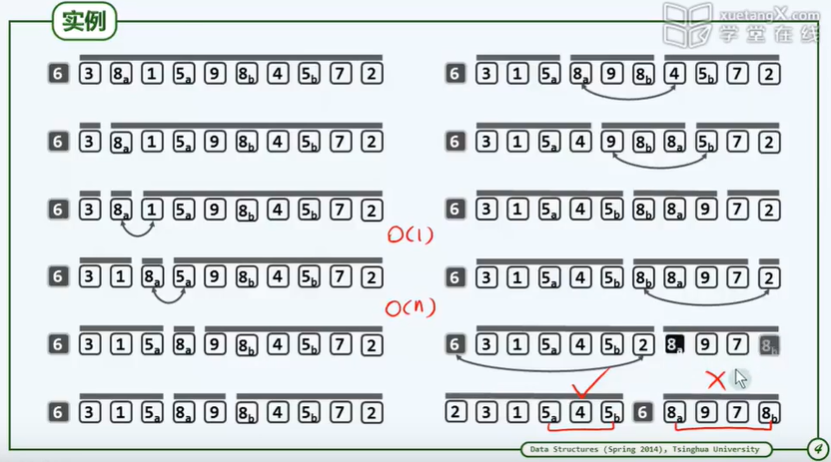
selection
The k-th largest element
Centered element
Select mode
P481
median
Traverse + count + take extreme value
template <typename T> bool majority(Vector<T> A, T& maj)
{
return majEleCheck(A, maj = median(A));
}
template <typename T> bool najiority(Vector<T> A, T& maj)
{
return majElecheck(A, maj = mode(A));
}
template <typename T> bool majority(Vector<T> A, T& maj)
{
return majEleCheck(A, maj = majEleCandidate(A));
}
Reduce and govern
template <typename T> T majEleCandidate(Vector<T> A) {
T maj; //Mode candidate
// Linear scanning: with the help of counter c, the difference between the number of maj and other elements is recorded
for(int c=0; i < A.size(); i++)
if (0 == c) {// Whenever c returns to zero, it means that the prefix p can be cut off
maj = A[i]; c = 1; // The mode candidate is changed to the new current element
}
else// otherwise
maj == A[i] ? c++ : c--; // Update the difference counter accordingly
return maj; //
}
quickSelect
P486
/* quickSelect()algorithm */
template <typename T> void quickSelect(Vector<T>& A, Rank k) {
for (Rank lo = 0, hi = A.size() - 1; lo < hi;) {
Rank i = lo, j = hi; T pivot = A[lo];
while (i < j) {// O(hi - lo + 1) = O(n)
while (i < j && pivot <= A[j]) j--; A[i] = A[j];
while (i < j && A[i] <= pivot) i++; A[j] = A[i];
}
A[i] = pivot;
if (k <= i) hi = i - 1;
if (i <= k) lo = i + 1;
}
}
Select the median from the vector with scale n, and the worst time complexity of quickselect algorithm is O(n^2)
linearSelect() algorithm
P487
Shell Sort
P491
1959
Matrix rearrangement: logically sort (call by rank)
Insert sort
Step sequence
Mutual prime
Insertion sort is sensitive to the order of the input sequence
Postage problem
Collect postage
linear combination
Theorem K (knuth)
Any sequence that was originally g-ordered will remain g-ordered after h-sorting.
The linear combination of ordered sequences is still ordered.
Insertion sort: the total number of inverse sequences will continue to decrease. The input is sensitive and linearly proportional to the number of inverse pairs.
Stability: Merge
Unstable: fast, heap, Hill
The median selection algorithm of linear time is very inefficient.
Prevent quick sort from becoming inefficient due to unbalanced pivot points:
Method 1: choose the middle of the three
Method 2: combine heap sort with quick sort