The Difference between Chain Storage Structure and Sequential Storage Structure
1. The memory address of the linked list storage structure is not necessarily continuous, but the memory address of the sequential storage structure must be continuous.
2. Chain storage is suitable for inserting, deleting and updating elements more frequently, while sequential storage structure is suitable for frequent queries.
How to understand the chain storage structure:
Like detective stories, the author will not let you know the whole story, but through the information on the scene or some judgment, step by step to achieve the designated link, that is to say, every step is to confirm the information and the next step of guidance. (Exclude some complicated cases with clues.)
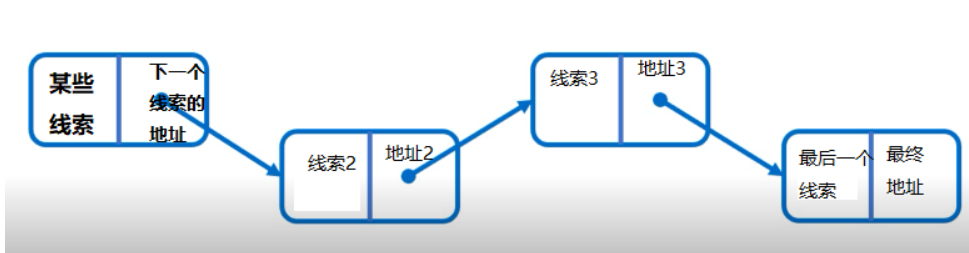
dynamic chain
1) node
In the sequential structure, each data element only needs to store data element information, but in the chain structure, it not only needs to store data element information, but also needs to store the storage address of its successor elements.
Unlike the sequential storage structure, which is similar to standing in a queue, it is equivalent to the random distribution of information in the memory space that everyone will take with them where they are going.
Therefore, in order to represent the logical relationship between each data element ai and its immediate successor element ai+1, besides storing its own information, data ai also needs to store a storage location indicating its immediate successor. We call the domain storing data element information as data domain, the domain storing direct successor location as pointer domain, and the information stored in pointer domain as needle or chain. The storage image of the data element ai composed of these two parts of information is called Node.
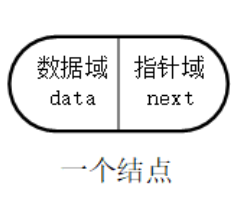
n nodes (storage image of ai) are linked into a linked list, which is a linear table (a1, a2, a3... The chain storage structure is called single linked list because there is only one pointer field in each node of the linked list.
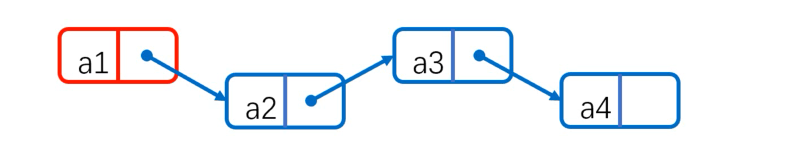
head node
We call the first node in the list as the head node. In the chain storage structure, the head node can be virtual and real, which means that the real head node stores information and the location of the subsequent nodes. The virtual head node does not store information. Its pointer domain stores pointers to the first node. The virtual head node is not really big. Brother, Brother is the next point that the pointer of his pointer field stores (but the virtual header node is the real node!!!).

A red node is a virtual header node. It does not store information, but only the address of the next node.
2) Head and tail pointers
For linear tables, there must always be a head and tail, and linked lists are no exception. We call the storage location of the first node in the list header pointer, so the whole list must be stored from the header pointer. Every node after that is where the successor pointer of the previous node points. So imagine where the last node points?
Finally, it means that direct succession does not exist, so the pointer of the last node of the linear list is null.
Header pointer: Just a reference variable, just a pointer to store the address of the header node.
Tail pointer: Represents the location of the last node in the list and stores the address of the last node.
When traversing the list, the tail pointer can be used as the termination condition. When the tail pointer points to NULL, it means that the list traversal is completed. It also reduces the time complexity of the tail insertion method, which only requires the tail pointer to move to the next node.
3) Insertion and deletion of linked list
insert
There are three kinds of insertion: head insertion, tail insertion and general insertion.
1. Head insertion;
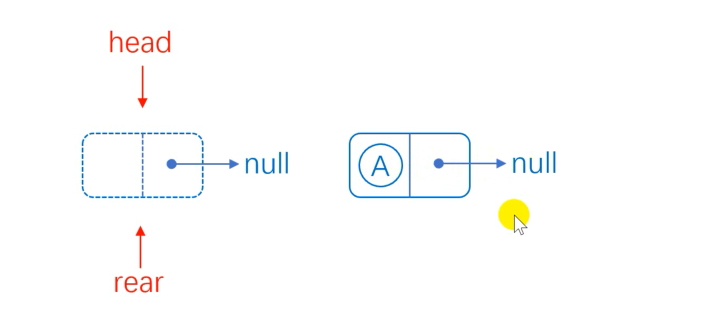
Head insertion has special circumstances. When the list is empty and a node is inserted, we can first give the next hop of the header node to the next hop of A, then give the address of A to the next hop of the header node, and then point back to A.
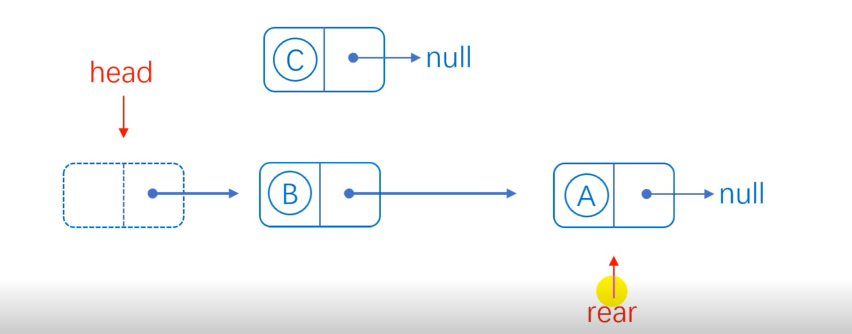
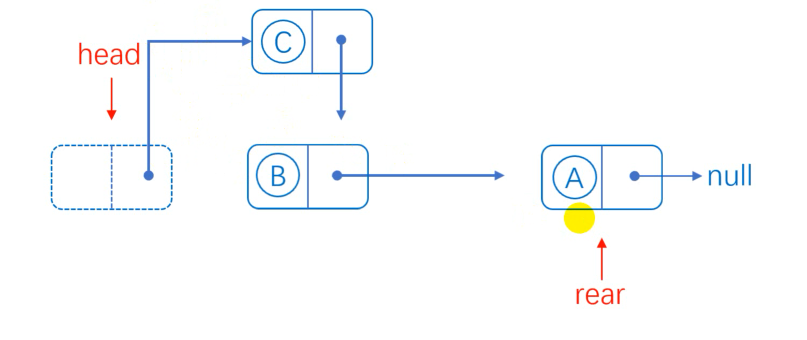
When the list is not empty, the next hop of the head node points to the next hop assigned to C, the next hop of the head node points to C, and the tail pointer does not need to move.
Tail insertion method
When the list is empty, we find that it is the same as head insertion.
When the list is not empty:
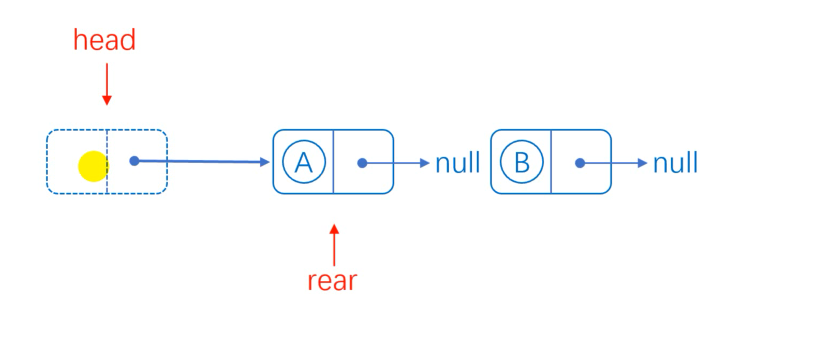
Give the next hop of the endpoint to the next hop of the new element B, and the next hop of the endpoint points to the new element B. Don't forget that the tail pointer needs to point to the new element.
(3) General insertion:
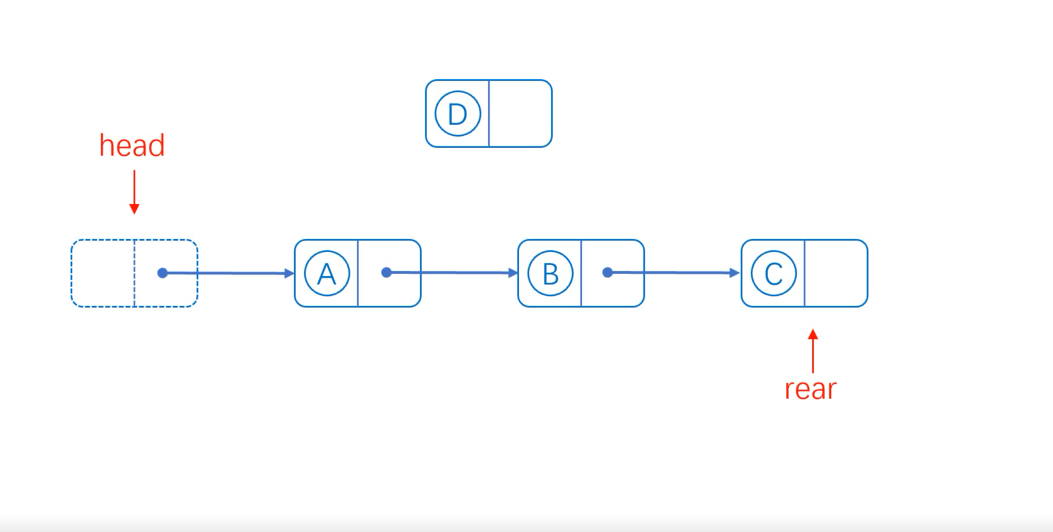
If we want to insert new element D between AB, we can regard A as a header node, so that we can use header interpolation to calculate the next hop of A to the next hop of D, and point the next hop of A to D.
delete
There are also three types of deletion: header deletion, tail deletion and general deletion.
First, delete:
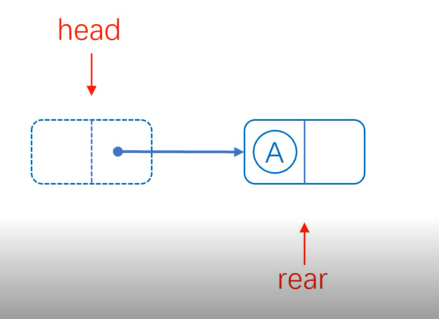
Head deletion is also a special case. When there is only one element in the list, the next hop of the head node is pointed to empty, and both the head pointer and the tail pointer are pointed to the head node (virtual head node).
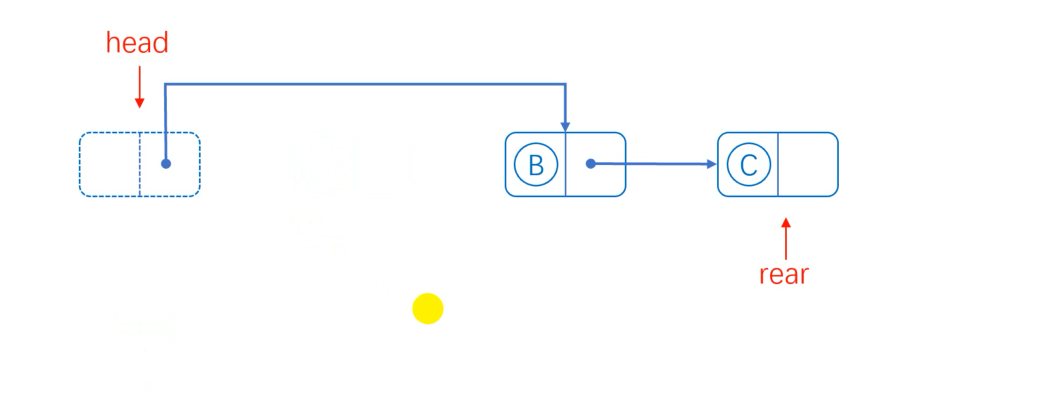
When the length of the list is longer than 1, delete B, just assign the next hop of B to the next hop of the head node, and then point the deleted element to empty.
Tail deletion
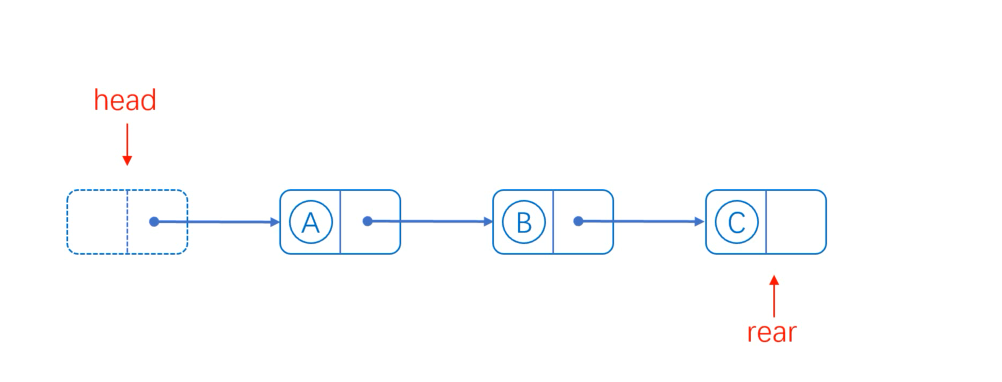
In tail deletion, we need to know the precursor of the endpoint (the list does not know where the end is, so we need to look from the beginning), point the next hop of the precursor B to null, and the tail pointer to the precursor.
(3) General deletion
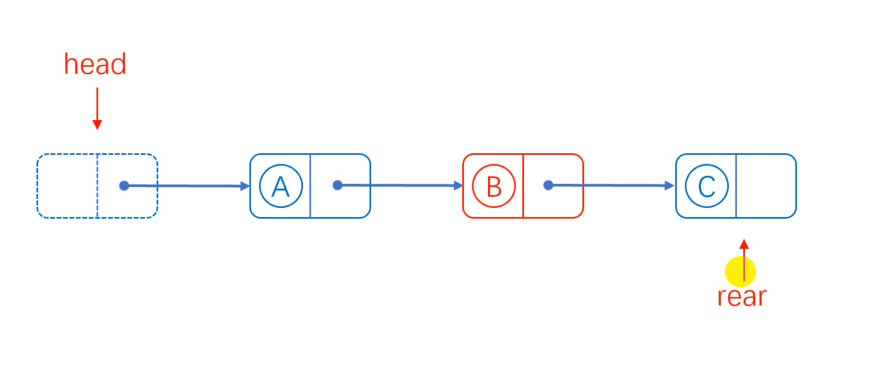

First, traverse the list, find the precursor A that needs to delete element B, assign the next hop of B to the next hop of A. The next hop of A points directly to C, then there is no element pointing to B, but B also points to C, so the next hop of B points to null, and B disappears!
How to Realize Linear Tables with Linked Lists
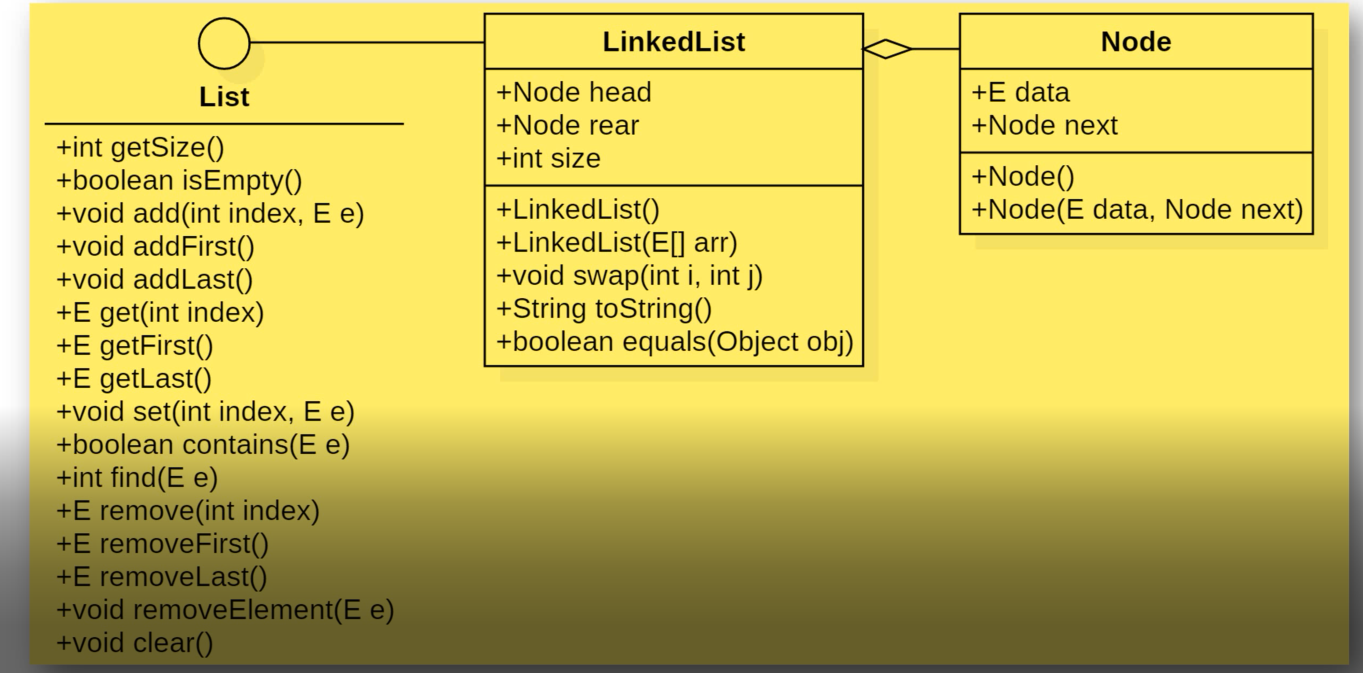
Using linked lists to implement linear lists or inheriting the List interface. Next is how to use the linked list to realize the function operation of the linear table (this time the linear table is realized by using the structure of virtual header nodes) (LinkedList)
Single linked list code implementation:
1) First, we define the List interface.
package com.openlab.list;
/**
* List Is the ultimate parent interface of a linear table
* @author ABC
* @param <E>
*/
public interface List<E> {
/**
* Get the number of elements in a linear table (the length of a linear table)
* @return The Number of Effective Elements in a Linear Table
*/
public int getSize();
/**
* Judging whether a linear table is empty
* @return Whether the Boolean type value is empty or not
*/
public boolean isEmpty();
/**
* Add element e to the index corner label specified in the linearity table
* @param index Specified corner label 0 <= index <= size
* @param e Elements to insert
*/
public void add(int index,E e);
/**
* Insert an element in the header position of a linear table
* @param e The element to be inserted is specified at corner zero
*/
public void addFirst(E e);
/**
* Insert an element at the end of the table of the linearity
* @param e The element to be inserted is specified at the corner size
*/
public void addLast(E e);
/**
* Get the element at the specified index corner in the linearity table
* @param index Specified corner label 0<=index<size
* @return The element corresponding to the corner label
*/
public E get(int index);
/**
* Get the elements of the header in a linear table
* @return Table header element index=0
*/
public E getFirst();
/**
* Getting the elements at the end of a linear table
* @return The element index at the end of the table = size-1
*/
public E getLast();
/**
* Modify the element at index specified in the linear table to a new element e
* @param index Designated corners
* @param e element fresh
*/
public void set(int index,E e);
/**
* Determine whether the linear table contains the specified element e by default
* @param e To determine whether elements exist or not
* @return Boolean Type Value of Element Existence
*/
public boolean contains(E e);
/**
* Get the label of the specified element e in the linearity table by default from before to after
* @param e Data to be queried
* @return Corner of data in linearity
*/
public int find(E e);
/**
* Delete the element at the specified corner label in the linearity table and return
* @param index Specified corner label 0<=index<size
* @return Remove old elements
*/
public E remove(int index);
/**
* Delete header elements from linear tables
* @return Header element
*/
public E removeFirst();
/**
* Delete tail elements in linear tables
* @return Table tail element
*/
public E removeLast();
/**
* Delete specified elements from a linear table
* @param e Specified element
*/
public void removeElement(E e);
/**
* Clear Linear Table
*/
public void clear();
}2) LinkedList implements List interface
The linked list is composed of many nodes. We can define a Node class to store the information of data items.
Since the node class we defined is not allowed to be manipulated by the outside world, the Node class is privatized and only allowed to be called in this class.
package com.openlab.lianbiao
public class LinkedList<E> implements List<E>{
private class Node{
E data;
Node next; //Pointer field, same data field
public Node() {
this(null,null);
}
public Node(E data,Node next) {
this.data=data;
this.next=null;
}
@Override
public String toString() {
return data.toString();
}
}
private Node head; //Head Pointer to Head Node
private Node rear; //End pointer to endpoint
private int size; //Number of recording elements
public LinkedList() {
head = new Node();
rear =head;
size=0;
}
public LinkedList(E[] arr) {//Constructive Functions with Parameters
this();
for(E e:arr) {
addLast(e);
}
}
@Override
public int getSize() { //Get the length of the linked list
return size;
}
@Override
public boolean isEmputy() {//Sentence blank
return size==0&&head.next==null;
3) Insert and delete
Insertion
@Override
public void add(int index, E e) {
if(index<0||index>size){ //Judging whether the adding position is legitimate
throw new IllegalArgumentException("Illegal insertion of corners!");
}
Node n=new Node(e,null);//Create new nodes
if(index==0){ //Head insertion
n.next=head.next;//Store the address of the real header node in the pointer field of the new node
head.next=n;//Replace the contents of the pointer field of the virtual header node with the address of the new node added
if(size==0){//Are there any elements in the list?
rear=n;//Point the tail pointer to the address of the new element
}
}else if(index==size){ //Tail insertion
rear.next=n;
rear=rear.next;
}else{//Intermediate interpolation
Node p=head;//Ab initio traversal
for(int i=0;i<index;i++){
p=p.next;//Find the precursor to delete the node
}
n.next=p.next;
p.next=n;
}
size++;
}
@Override
public void addFirst(E e) {//Head insertion
add(0,e);
}
@Override
public void addLast(E e) {//Tail insertion
add(size,e);
}
@Override
public E get(int index) {
if(index<0||index>=size){
throw new IllegalArgumentException("Illegal corner marking!");
}
if(index==0){
return head.next.data;
}else if(index==size-1){
return rear.data;
}else{
Node p=head;
for(int i=0;i<=index;i++){
p=p.next;
}
return p.data;
}
}
@Override
public E getFirst() {
return get(0);
}
@Override
public E getLast() {
return get(size-1);
}
@Override
public void set(int index, E e) {
if(index<0||index>=size){
throw new IllegalArgumentException("Illegal modification of corner markers!");
}
if(index==0){
head.next.data=e;
}else if(index==size-1){
rear.data=e;
}else{
Node p=head;
for(int i=0;i<=index;i++){
p=p.next;
}
p.data=e;
}
}
@Override
public boolean contains(E e) { //Determine whether an element is included
return find(e)!=-1;
}
@Override
public int find(E e) {
int index=-1;
if(isEmpty()){
return index;
}
Node p=head;
while(p.next!=null){
p=p.next;
index++;
if(p.data==e){
return index;
}
}
return -1;
}
Delete
@Override
public E remove(int index) { //Input Corner Deletes Corresponding Nodes
if(index<0||index>=size){ //Judgment of legality
throw new IllegalArgumentException("Deleting corner labels is illegal!");
}
E res=null;
if(index==0){ //Header deletion
Node p=head.next;
res=p.data;
head.next=p.next;
p.next=null;
p=null;
if(size==1){ //In special cases, there is only one node left.
rear=head; //Tail pointer forward
}
}else if(index==size-1){//Tail deletion
Node p=head;
res=rear.data;
while(p.next!=rear){
p=p.next;
}
p.next=null;
rear=p;
}else{
Node p=head;
for(int i=0;i<index;i++){
p=p.next;
}
Node del=p.next;
res=del.data;
p.next=del.next;
del.next=null;
del=null;
}
size--;
return res;
}
@Override
public E removeFirst() {
return remove(0);
}
@Override
public E removeLast() {
return remove(size-1);
}
@Override
public void removeElement(E e) { //find the element, return the corner mark and delete it
int index=find(e);
if(index==-1){
throw new IllegalArgumentException("Element does not exist");
}
remove(index);
}
@Override
public void clear() {
head.next=null;
rear=head;
size=0;
}
(3) Rewrite toString
@Override
public String toString() {
StringBuilder sb=new StringBuilder();
sb.append("LinkedList:size="+getSize()+"\n");
if(isEmpty()){
sb.append("[]");
}else{
sb.append("[");
Node p=head;
while(p.next!=null){
p=p.next;
if(p==rear){
sb.append(p.data+"]");
}else{
sb.append(p.data+",");
}
}
}
return sb.toString();
}