List

1. Introduction

1.1. Abstract Data Types(ADTS)

1. ADT definition: a set of objects together with a set of operations Abstract data types are mathematical abstractions; nowhere in an ADT‟s definition is there any mention of how the set of operations is implemented. A set of objects and a set of operations. Abstract data types are mathematical abstractions; In the definition of ADT, there is no mention of how to implement the operation set.

1.1.1. data object

1.1.2. data structure

2. Linearity table

1. A linear table is a collection of objects or values

1. The above is the method to be implemented.

2.1. Methods to implement linear table

2.2. Different implementations of linear tables

2.2.1. Simple array implementation of linear table

1. (e1,e2,...... en), that is, the array requests a continuous piece of memory from the system, and the size of the data is determined by the programmer.
2. each position of the array is called a cell or a node mapping formula: location(i)=i-1
3. The complexity of extracting an element from the linear table stored in the array type is O(1).
4. Generally, we place values of the same type in the linear table.

Some methods

1. Time complexity O(n) and average algorithm complexity O((n+1)/2) of sequential Search(x)
   • Average data access times: n/2
2. delete the k'th element and return it in x
   • The algorithm complexity in the worst and average cases is O(n)
   • Average number of data moves: (n-1)/2
3. Insert operation insert(x,i)
   • Average number of data moves: n/2

2.2.2. A linked list implements a linear table

1. Features: not continuous memory in memory.
2. A linked list node stores a pointer and data.
   • Pointers in java cannot be added or subtracted to prevent some system problems. In C + +, addition and subtraction can be performed.
3. The last pointer points to null

Partial operation

1. Delete operation: Delete(index,x)
   1. Delete the first node: re point to the first pointer, and delete the dereferenced object in C + +. Manual release needs to write down the position first.
   2. Delete intermediate node: query first and then delete
      • before.link = before.link.link
2. Insert operation: insert(index,x)
   1. Insert an element at the beginning of the linear table: first insert an element, and then point the head pointer to the head.
   2. Insert an element in the middle of the linear table: first query to find the corresponding element

2.2.3. Single linked list with header element

1. There is a Header node, Header: there is no data in this node, and then the pointer points to the first element

3. java implementation of linear table

1. ListNode: class representing the node
2. LinkedList: a class representing the table itself
3. LinkedListItr: class representing cursor position
4. Are part of the package DataStructure

3.1. ListNode

class ListNode {   
    object element;
    ListNode next;
    ListNode( object theElement) {
        this( theElement, null);
    }
    ListNode( object theElement, ListNode n) {
        element = theElement; 
        next = n;
    }
} 

3.2. LinkedListItr

1. Encapsulate the corresponding pointer operation

public class LinkedListItr {
    LinkedListItr( ListNode  theNode) {
        current = theNode;
    }
    public boolean isPastEnd( ) {
        return current == null; 
    }
    public object retrieve() {
        //Get current node data
        return isPastEnd( ) ? null : current.element; 
    }
    public void advance( ) {
        if( ! isPastEnd( ) ) current = current.next; 
    }
    ListNode current; 
}

3.3. LinkedList

public class LinkedList {
    private ListNode header;
    public LinkedList( ) {//Here is a single linked list with header node. If there is no header, it should be heder = null
        header = new ListNode( null );
    }
    public boolean isEmpty( ) {
        return header.next = = null ;
    }
    public void makeEmpty( ) {
        header.next = null;
    }
    //Itr pointing to head pointer
    public LinkedListItr zeroth( ) {
        return new LinkedListItr( header );
    }
    //Itr pointing to the first item
    public LinkedListItr first( ) {
        return new LinkedListItr( header.next );
    } 
    public LinkedListItr find( object x )
    public void remove( object x )
    public LinkedListItr findPrevious( object x )
    public void insert( object x, LinkedListItr p )
}

3.4. Implementation of some methods

3.4.1. Print linear table

//Method to print a list
public static void printList( LinkedList theList ) {   
    if ( theList.isEmpty( ) ) 
        System.out.print ("Empty list");
    else {
        LinkedListItr itr = theList.first();
        for(;! Itr.isPastEnd(); itr. Advance( ) )
            System.out.print(itr.retrieve() + " " );
    }
    System.out.println();
}

3.4.2. Find specific items

public LinkedListItr find (object x) {
    ListNode itr = header.next;
    while ( itr != null && !itr.element.equals( x ))
        itr = itr.next;
        return new LinkedListItr( itr );
} 

1. Time complexity O(n)

3.4.3. Remove node

public void remove( object x ) {
    LinkedListItr p = findprevious( x );
    if( p.current.next != null )
        p.current.next = p.current.next.next;
}

1. Time complexity O(1)
   • You can treat the findPrevious operation as a separate operation, not a part of this operation.

3.4.4. Find previous node

public LinkedListItr findPrevious( object x ) {
    ListNode itr = header;
    while( itr.next !=null && !itr.next.element.equals( x )) itr = itr.next;
    return new LinkedListItr( itr );
}

1. Time complexity O(n)

3.4.5. Example: polynomial summation

1. We sum two polynomials
2. Method 1: we align and add
3. Method 2: we use arrays to store indices and parameters.

public class Polynomial {
    public Polynomial( ) {
        zeroPolynomial( );
    }
    public void insertTerm( int coef, int exp )
    public void zeroPolynomial(){//Empty polynomial
        for( int i = 0; i<=MAX-DEGREE; i++) 
            coeffArray[i] = 0;
        highPower = 0; 
    }
    public Polynomial add( Polynomial rhs ){
        Polynomial sum = new Polynomial( );
        sum.highPower = max( highPower, rhs.highPower );
        for( int i = sum.highPower;  i>=0;  i--)
            sum.coeffArray[i] = coeffArray[i] + rhs.coeffArray[i];
        return sum; 
    }
    public Polynomial multiply( Polynomial rhs ) throws Overflow
    public void print( )
    public static final int MAX-DEGREE = 100;
    private int coeffArray[ ] = new int [MAX-DEGREE + 1];
    private int highPower = 0;
}

4. Single cycle linked list

1. The next of the last one points to the first or header

4.1. example

1. josephus problem
   

2. Problem solving:

   • Use a new single linked list to record.
   • p is the last point to reduce the complexity of insertion

w = m;
for( int i = 1; i<= n-1; i++) {
    for (int j = 1; j<=w-1; j++) rear = rear.link;
    if (i = = 1) { 
        head = rear.link ; p = head;
    } else { 
        p.link = rear.link;
        p = rear.link;
    }
    rear.link = p.link;
    }
    P.link = rear; rear.link = null;

4.2. Relevant calculation formulas of circular queue

1. We might as well set front as the head pointer, rear as the tail pointer, and m as the maximum capacity of the queue.

1. Join the team: rear = (rear + 1)% m

2. Outgoing: front = (front + 1)% m

3. front = rear

4. Full team: front = (rear + 1)% m

5. Number of elements in the current queue: n = (Rear - front + m)% m

6. Find the position of the team head pointer: (Rear - length + 1 + m)% m

7. Relevant calculation formulas of circular queue

5. Polynomial problem

5.1. Array implementation of linear table

5.1.1. Partial method

multiplication

5.2. Single linked list implementation of linear table

5.2.1. Polynomial addition

1. Store the coefficients and indexes of non-zero indexes, so no node is composed of three fields.
   • (coef + exp)(item) + link
2. In the specific implementation, do not re apply for nodes, and make full use of the nodes of the original two linked lists.
3. Method: Set 4 reference variables:
   • PA, Pb, PC, P (required for C + +)

Arithmetic steps

1. Initialization: PC, PA, Pb
2. When both pa and pb have entries, pc always points to the last node of the result list when adding.
   1. Exponential equality (pa. exp==pb. exp)
      • Corresponding coefficient addition: Pa. coef = Pa. coef + Pb coef ;
      • P = Pb (required for C + +);
      • pb advance;
      • if (the coefficient addition result is 0) {P = Pa; PA forward;} Else {PC. link = Pa; PC = Pa; PA forward}
   2. Exponential inequality Pa. exp < Pb Exp / / Pb to insert the linked list of results
      • {PC. link = Pb; PC = Pb; Pb forward}
   3. Exponential inequality Pa. exp > Pb Exp / / PA to insert the linked list of results
      • {PC. link = Pa; PC = Pa; PA forward}
3. When one of the two linked lists is empty, the other linked list can be linked into the result linked list. if(pb is empty) {pc. link=pa;} else pc. link=pb;

Algorithm complexity: O(m+n)

6. Two way linked list

1. When deleting, the middle is different

6.1. delete

1. Delete the first node
   
2. Delete middle
   

6.2. insert

1. Insert from scratch
   
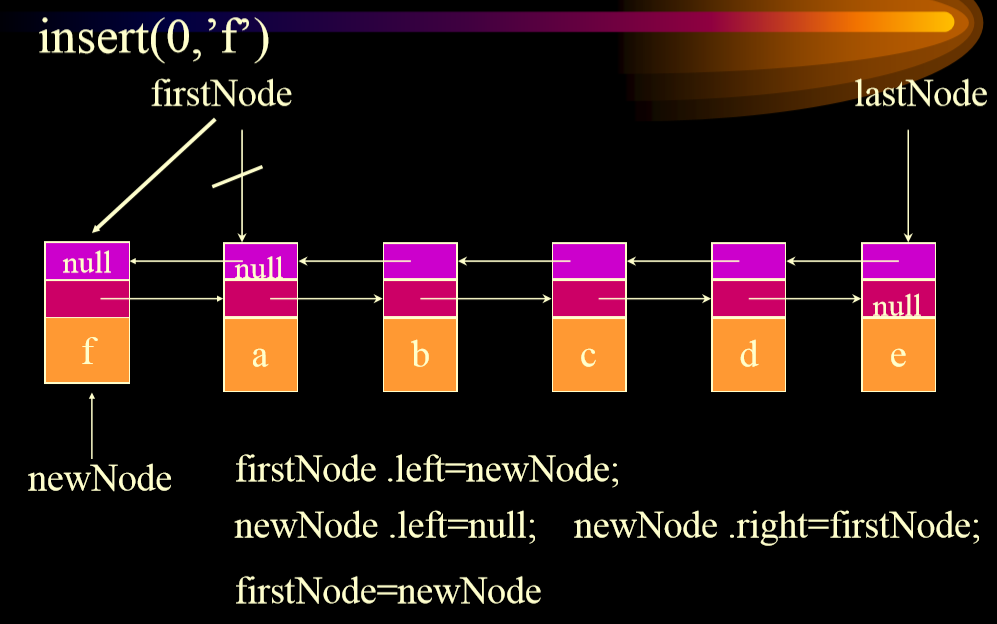
2. Insert from
   

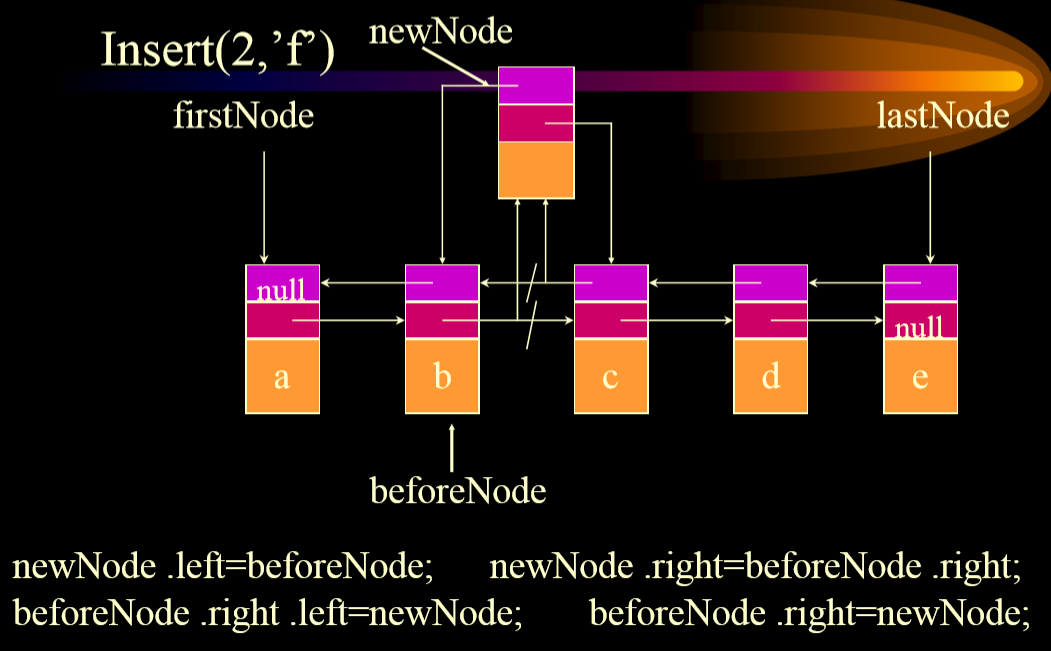
6.3. Deformation: bidirectional circular linked list

1. Bidirectional linked list with header
2. Bidirectional linked list without header
3. Empty bidirectional linked list with header

7. Example: 2009 postgraduate entrance examination questions

1. Algorithm idea: Double pointers. The first pointer runs k steps first, then runs the second pointer, and the first and second run forward together.

8. Static linked list

1. Static linked list is a single linked list implemented by array.

1. In the system, for the system, memory is managed by the system like this.
2. If next is 0, it is equivalent to null

8.1. Implementation of static linked list

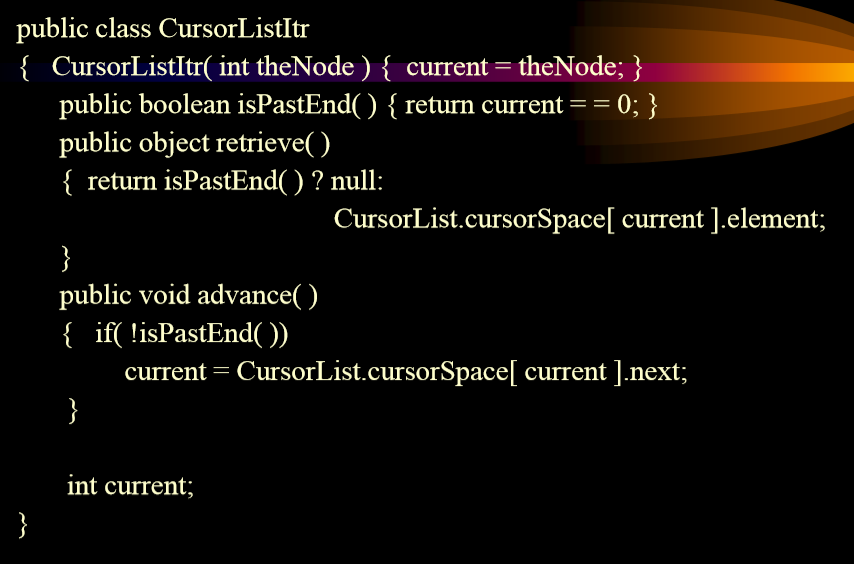
8.2. Implementation code

//Class skeleton for CursorList 
public class CursorList {
    private static int alloc( )
    private static void free( int p)
    public CursorList( ) {  header = alloc( );   cursorSpace[ header ].next = 0; }
    public boolean isEmpty( ) {  return cursorSpace[ header ].next = = 0; }
    public void makeEmpty( )
    public CursorListItr zeroth( ) {   return new CursorListItr( header ); }
    public CursorListItr first( ) {   return new CursorListItr( cursorSpace[ header ].next ); }
    public CursorListItr find( object x )
    public void insert( object x, CursorListItr p)
    public void remove( object x )
    public CursorListItr findPrevious( object x )
    private int header; static CursorNode [ ] cursorSpace;
    private static final int SPACE-SIZE = 100;
    static {//There is only one static variable for a class
        cursorSpace = new CursorNode[ SPACE-SIZE ];
        for( int i = 0; i<SPACE-SIZE; i++) cursorSpace[ i ] = new CursorNode( null, i + 1 );
        cursorSpace[ SPACE-SIZE-1].next = 0;
    }
}

1. The static part is the responsibility of the system manager
2. The non static part is user's

8.3. How does the static linked list determine that there is still memory that can be allocated

1. Store the remaining memory in a static linked list first.

8.4. Implementation of some methods

private static int alloc( ) {
    int p = cursorSpace[ 0 ].next;
    cursorSpace[0].next = cursorSpace[p].next;
    if( p == 0 ) throw new OutOfMemoryError( ); return p; }
private static void free( int p ) {
    cursorSpace[p].element = null;
    cursorSpace[p].next = cursorSpace[0].next;
    cursorSpace[0].next = p; }
public CursorListItr find( object x ) {
    int itr = cursorSpace[ header ].next;
    while( itr != 0 && !cursorSpace[ itr ].element.equals( x ) )
        itr = cursorSpace[ itr ].next;
    return new CursorListItr( itr );
}
public void insert( object x, CursorListItr p ) {
    if( p != null && p.current != 0) {
        int pos = p.current;
        int tmp = alloc( );
        cursorSpace[ tmp ].element = x;
        cursorSpace[ tmp ].next = cursorSpace[ pos ].next;
        cursorSpace[ pos ].next = tmp;
    }
}
public void remove( object x ) {   
    CursorListItr p = findPrevious( x );
    int pos = p.current;
    if( cursorSpace[ pos ].next != 0 ) {
        int tmp = cursorSpace[ pos ].next;
        cursorSpace[ pos ].next = cursorSpace[ tmp ].next;
        free( tmp );
    }
}
public void makeEmpty( ) {
    while( !isEmpty( ) )
        remove( first( ).retrieve( ) );
}