(1) Basic concepts of search

• Static lookup: Find only specific elements or their attributes
• Dynamic lookup: In addition to the above, there are insertion and deletion operations.
• Key words: primary keywords, sub-keywords.

(2) Sequential Search Method

• Starting from the last record of the table, the keywords of the record are compared with the given value one by one. If they are equal, the search succeeds, and if they are not equal until the first record, the search fails.

//Sequential storage structure of static lookup table
typedef struct{
	EkemType *elem;//Data Element Storage Space Base Address
	int  length;//Table Length
}SSTable;

int Search_Seq(SSTable ST,KeyType key){
	//In the sequence table ST, the data elements whose key is equal to key are searched sequentially.
	//If found, the function value is the position of the element in the table, otherwise 0
	ST.elem[0].key=key; //Sentry
	for(i=ST.length; !EQ(ST.elem[i].key,key);--i);//Look back and forth
	return i；//When not found, i is 0
}//Search.Seq

• Average search length ASL=3/4 (n+1)

(3) Half-fold Search Method

• First determine the scope of the records to be checked, then narrow the scope one by one until they are found or not found.

int Search_Bin(SSTable ST,KeyType key)
{
	low=1;high=ST.length;//Interval Initial Value
	while(low<=high)
	{
		mid=(low+high)/2;
		if(EQ(key,ST.elem[mid].key)) high=mid-1;
		else low=mid+1;
	}
	return 0; //There are no pending elements in the sequence table
}

• The maximum number of successful/unsuccessful comparison keywords for half-search is
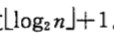
• The average search length is
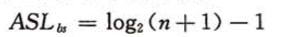
• Half-fold lookup is more efficient than sequential lookup, but half-fold lookup is only used in ordered tables and is limited to sequential storage structure (it is impossible to half-fold linear linked lists).

(4) Dynamic lookup table

• Binary Sort Tree (also known as Binary Search Tree)
  Empty tree; or left subtree is smaller than root node, right subtree is larger than root node, left and right subtrees of left and right subtrees all meet the above conditions.
  The storage structure is a binary linked list.

BiTree SearchBST(BiTree T,KeyType key, BiTree f, BiTree &p)
{
	//Recursive lookup of data elements whose keyword equals key in the binary sorting tree indicated by the root pointer T
	//If successful, pointer p points to the element node and returns TRUE, otherwise pointer p points to the access on the lookup path.
	//The last node returns to False, pointer f points to T's parents, and its initial call value is NULL
	if (!T) {p=f;return FALSE;} //Unsuccessful search
	else if EQ(key,T->data.key){P=t;return TURE;} //Find Success
	else if LT(key,T->data.key) return(SearchBST(T->lchild,key));//Continue searching in the left subtree
	else return(SearchBST(T->rchild,key));//Continue searching in the right subtree
}

// Insert

Status InsertBST(BiTree &T, ElemType e)
{
	//When there is no data element whose key is equal to e.key in the binary sorting tree T
	//Insert e and return TRUE, otherwise return FALSE
	if(!SearchBST(T,e.key,NULL,p){   //Unsuccessful search
	s=(BiTree)malloc(sizeof(BiTNode));
	s->data=e; s->lchild=s->rchild=NULL;
	if(!p) T=s;//The inserted node*s is a new root node
	else if LT(e.key,p->data.key) p->lchild=s; //The inserted node * s is the left child
	else p->rchild=s;
	return TRUE;
})
else return FALSE;//There are already nodes with the same keywords in the tree, and they are no longer inserted.
}

// Delete

Status DeleteBST(BiTree &T,KeyType key)
{
	//If there is a data element node whose key is equal to key in the binary sorting tree T,
	//And return True, or FALSE
	if(!T) return FALSE;//There is no element whose keyword equals key.
	else{
		if(EQ(key,T->data.key)){return Delete(T)};//Find data elements with keys equal to keys
		else if (LT(key，T->data.key))return DeleteBST(T->lchild,key);
		else return DeleteBST(T->rchild,key);
}
}

Status Delete(BiTree &p)
{
	//Delete the node p from the binary sorting tree and join its left or right subtrees
	if(!p->rchild)//The right subtree empty only needs to reconnect its left subtree
	{
		q=p;p=p->lchild;free(q);
	}
	else if(!p->lchild)
	{
		q=p;p=p->rchild;free(q);
	}
	else{//Neither left nor right subtrees are empty
		q=p;s=p->lchild;
		while(s->rchild){q=s;s=s->rchild}//Turn left, then right to the end.
		p->data=s->data;//s points to the "precursor" of the deleted node
		if(q!=p)q->rchild=s->lchild;//Right subtree of * q
		else q->lchild=s->lchild;
		delete s;
}
return TRUE;
}

• balanced binary tree
  Also called AVL tree. An empty tree or a left subtree and a right subtree are balanced binary trees, and the absolute value of the difference between the depth of the left subtree and the right subtree (balance factor: -1, 0, 1) is not more than 1.
  (Picture Title) The binary sorting tree is transformed into a balanced binary tree.
• B-Tree and Its Basic Operations
  A B-tree of order m is either an empty tree or an m-fork tree satisfying the following characteristics:
  There are at most m sub-trees at each node in the tree.
  2 If the root node is not the leaf node, there are at least two subtrees.
  3 All non-terminal nodes except root have at least [m/2] subtrees
  4 All non-terminal nodes contain the following information data, where k is the keyword and Ki < ki + 1; A is the pointer to the root node of the subtree, and the keywords of all nodes in the subtree indicated by the pointer Ai-1 are less than Ki, the keywords of all nodes in the subtree indicated by A n are greater than Kn, n is the number of keywords, and n+1 is the number of subtrees.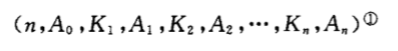
  5 All leaf nodes appear at the same level without information.
  B-tree is mainly used as the index of documents, so its search involves access to other villages.
• How to insert and delete B tree?
  Graphic and Textual Demonstration: https://www.cnblogs.com/nullzx/p/8729425.html

(5) Hash table
The storage address corresponds to the stored value. Storage location is called hash address or hash address.
(6) Analysis and Application of Search Algorithms