1. Concept introduction

In order structure and balance tree, there is no corresponding relationship between element key and its storage location. Therefore, when looking for an element, it must be compared many times by key. It depends on the complexity of the search tree (n), that is, the search efficiency is the balance of the search tree (n)
Number of element comparisons.

Ideal search method: you can get the elements to be searched directly from the table at one time without any comparison. If a storage structure is constructed to establish a one-to-one mapping relationship between the storage location of an element and its key code through a function (hashFunc), the element can be found quickly through this function.

When adding to the structure

• Insert element: calculate the storage location of the element with this function according to the key of the element to be inserted, and store it according to this location
• Search element: perform the same calculation on the key code of the element, take the obtained function value as the storage location of the element, and compare the elements according to this location in the structure. If the key codes are equal, the search is successful

This method is called hash (hash) method. The conversion function used in hash method is called hash (hash) function, and the structure constructed is called hashtable (or Hash list)

For example: data set {1, 7, 6, 4, 5, 9};
The hash function is set to: hash (key) = key% capacity; Capacity is the total size of the underlying space of the storage element.

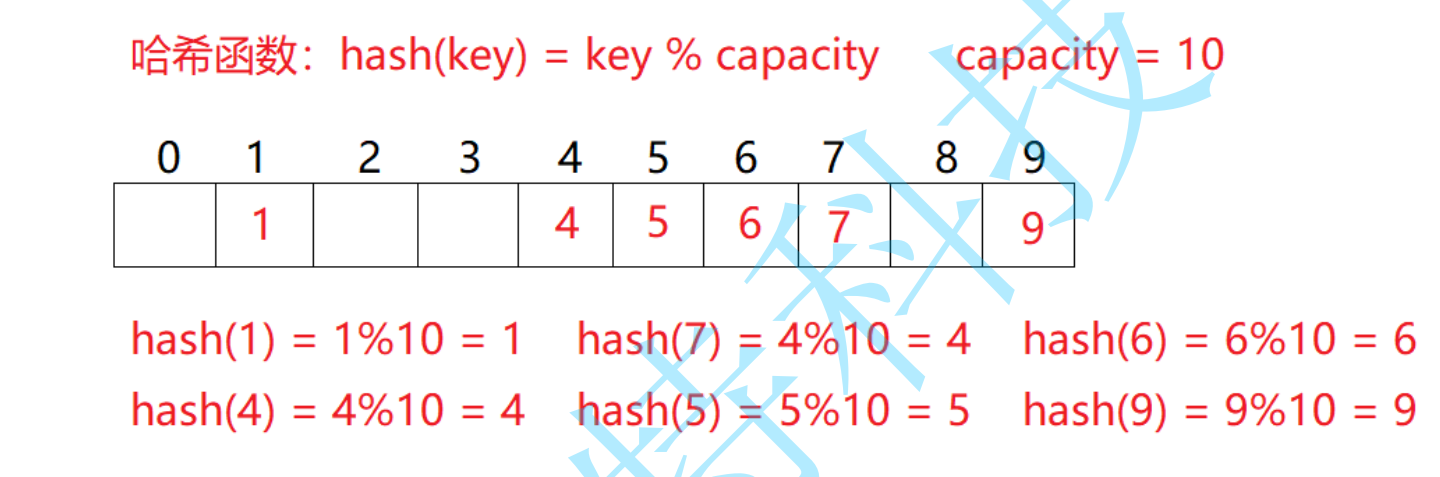
Using this method to search does not need to compare multiple key codes, so the search speed is relatively fast

2. Conflict

2.1 concept

For the keyword sum of two data elements (I! = J), there is! =, However, there are: hash () = = hash (), that is, different keywords calculate the same hash address through the same hash number. This phenomenon is called hash collision or hash collision. Data elements with different keys and the same hash address are called "synonyms".

2.2 avoidance

First of all, we need to make it clear that the capacity of the underlying array of our hash table is often less than the actual number of keywords to be stored, which leads to a problem. The occurrence of conflict is inevitable, but what we can do is to reduce the conflict rate as much as possible.

2.3 conflict avoidance hash function design

One reason for hash conflict may be that the hash function design is not reasonable. Design principle of hash function:

• The definition field of hash function must include all keys to be stored. If the hash table allows m addresses, its value field must be between 0 and m-1
• The address calculated by hash function can be evenly distributed in the whole space
• Hash functions should be simple

Common hash functions

1. Direct customization method – (common)
   Take a linear function of the keyword as the Hash address: Hash (Key) = A*Key + B advantages: simple and uniform disadvantages: you need to know the distribution of keywords in advance. Usage scenario: it is suitable for finding small and continuous situations Interview question: the first character in the string appears only once
2. Division and remainder method – (common)
   Let the number of addresses allowed in the hash table be m, and take a prime number p not greater than m but closest to or equal to m as the divisor, according to the hash function:
   Hash (key) = key% P (P < = m), convert the key code into hash address
3. Square middle method – (understand)
   Assuming that the keyword is 1234, its square is 1522756, and the middle three bits 227 are extracted as the hash address; For another example, if the keyword is 4321, its square is 18671041. It is more suitable to extract the middle three bits 671 (or 710) as the square median of the hash address: the distribution of keywords is not known, and the number of bits is not very large
4. Folding method – (understand)
   The folding method is to divide the keyword from left to right into several parts with equal digits (the digits of the last part can be shorter), then overlay and sum these parts, and take the last few digits as the hash address according to the length of the hash table.
   The folding method is suitable for the situation that there is no need to know the distribution of keywords in advance and there are many keywords
5. Random number method – (understand)
   Select a random function and take the random function value of the keyword as its hash address, that is, H(key) = random(key), where random is a random number function.
   This method is usually used when the keyword length is different
6. Mathematical analysis – (understanding)
   There are n d digits, and each bit may have r different symbols. The frequency of these r different symbols may not be the same in each bit. They may be evenly distributed in some bits, and the opportunities of each symbol are equal. They are unevenly distributed in some bits, and only some symbols often appear. According to the size of the hash table, several bits in which various symbols are evenly distributed can be selected as the hash address.

Digital analysis method is usually suitable for dealing with the situation of large number of keywords, if the distribution of keywords is known in advance and several bits of keywords are evenly distributed

The more sophisticated the hash function is designed, the lower the possibility of hash conflict, but hash conflict cannot be avoided

2.4 conflict avoidance load factor adjustment (key)

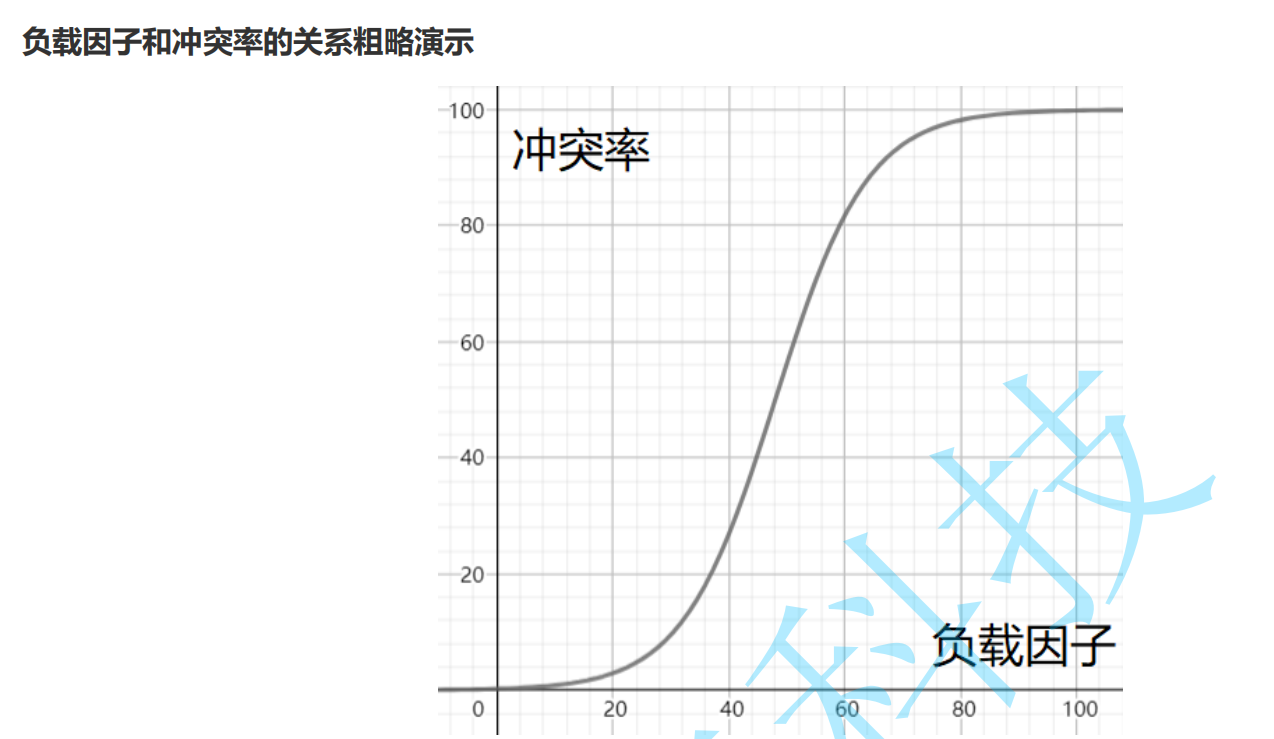
Therefore, when the conflict rate reaches an intolerable level, we need to reduce the conflict rate in disguise by reducing the load factor.
Given that the number of existing keywords in the hash table is immutable, all we can adjust is the size of the array in the hash table.

2.5 conflict resolution

There are two common ways to resolve hash conflicts: closed hash and open hash

2.5.1 closed hash

Closed hash: also known as open addressing method. In case of hash conflict, if the hash table is not full, it means that there must be an empty position in the hash table, then the key can be stored in the "next" empty position in the conflict position.

How to find the next empty location:

1. Linear detection
   For example, in the above scenario, you need to insert element 44. First calculate the hash address through the hash function with the subscript of 4. Therefore, 44 should be inserted in this position theoretically, but the element with the value of 4 has been placed in this position, that is, hash conflict occurs.

Linear detection: start from the conflicting position and detect backward in turn until the next empty position is found.

• insert

1. Obtain the position of the element to be inserted in the hash table through the hash function
2. If there is no element in this position, insert the new element directly. If there is a hash conflict in this position, use linear detection to find the next empty position and insert the new element
   

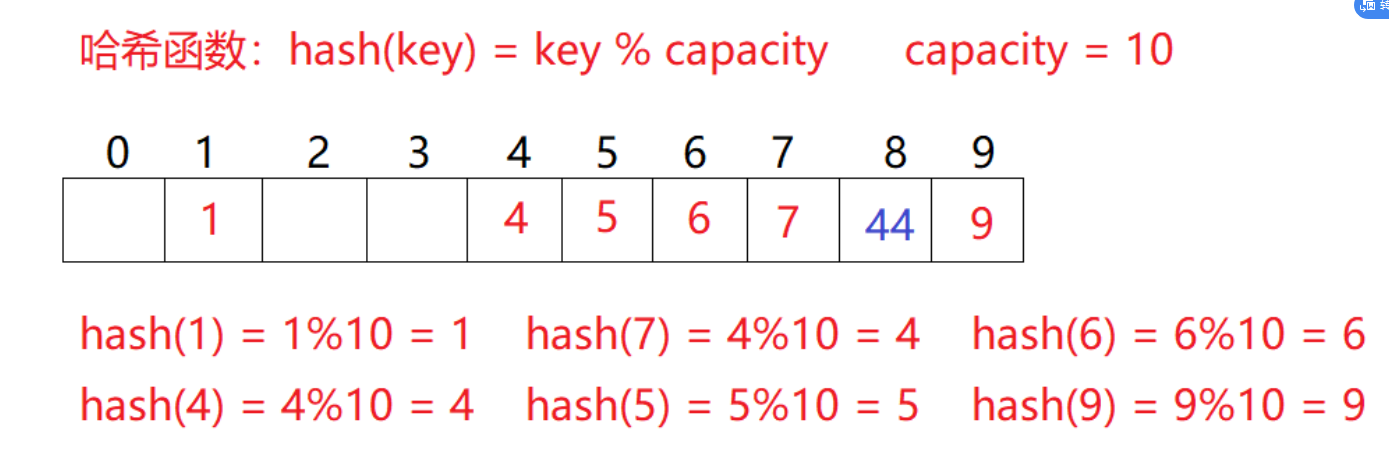
• When using closed hash to deal with hash conflicts, the existing elements in the hash table cannot be deleted physically. If the elements are deleted directly, the search of other elements will be affected. For example, if element 4 is deleted directly, 44 searching may be affected. Therefore, linear detection uses the marked pseudo deletion method to delete an element.

1. Secondary detection (use specific formula to avoid data being placed next to each other)
   The defect of linear detection is that conflicting data are stacked together, which has something to do with finding the next empty position. Because the way to find the empty position is to find it one by one next to each other, in order to avoid this problem, the method to find the next empty position for secondary detection is: Hi = (H0 + I ^ 2)% m, or: Hi
   = (H0 -i^2 )% m. Where: i = 1,2,3..., H0 is the position obtained by calculating the key of the element through the hash function Hash(x), and M is the size of the table.

The research shows that when the length of the table is a prime number and the table loading factor A does not exceed 0.5, the new table entry can be inserted, and any position will not be explored twice. Therefore, as long as there are half empty positions in the table, there will be no problem of full table. When searching, you can not consider the situation that the table is full, but when inserting, you must ensure that the loading factor a of the table does not exceed 0.5. If it exceeds, you must consider increasing the capacity.

Therefore, the biggest defect of hash ratio is the low space utilization, which is also the defect of hash.

2.6 conflict resolution hash / hash bucket (array + linked list)

The open hash method, also known as the chain address method (open chain method), first uses the hash function to calculate the hash address of the key code set. The key codes with the same address belong to the same subset. Each subset is called a bucket. The elements in each bucket are linked through a single linked list, and the head node of each linked list is stored in the hash table.

2.7 solutions in case of serious conflict

In fact, the hash bucket can be regarded as transforming the search problem of large sets into the search problem of small sets. If the conflict is serious, it means that the search performance of small sets is actually poor. At this time, we can continue to transform the so-called small set search problem, for example:

1. Behind each bucket is another hash table
2. Behind each bucket is a search tree

3. The key Val values are assumed to be the code implementation of int type

public class HashBuck {
    static class Node{
        public int key;
        public int val;
        public Node next;

        public Node(int key,int val){
            this.key=key;
            this.val=val;
        }
    }

    public Node[] array;
    public int usedSize;

    public static final double DEFAULT_LOAD_FACTOR=0.75;

    public HashBuck(){
        this.array=new Node[10];
    }

    /**
     * put function
     * @param key
     * @param val
     */
    public void put(int key,int val){
        //1. Find the location of the key
        int index=key%this.array.length;
        //2. Traverse the linked list of this subscript to see if the same key has an updated val value
        Node cur=array[index];
        while (cur!=null){
            if (cur.key==key){
                cur.val=val;//Update the value of val
                return;
            }
            cur=cur.next;
        }
        //3. If there is no such key, use the header insertion method
        Node node=new Node(key,val);
        node.next=array[index];
        array[index]=node;
        this.usedSize++;
        //4. After the element is successfully inserted, check the load factor of the current hash table
        if (loadFactor()>=DEFAULT_LOAD_FACTOR){

        }

    }

    private void resize(){
        Node[] newArray=new Node[array.length*2];
        //After capacity expansion, all elements need to be hashed again
        for (int i = 0; i < array.length; i++) {
            Node cur=array[i];
            while (cur!=null){
                int index=cur.key%newArray.length;//Get new subscript
                //Re hashing: the cur node is inserted into the linked list corresponding to the subscript of the new array in the form of head insertion / tail insertion
                Node curNext=cur.next;
                cur.next=newArray[index];//Bind first and then
                newArray[index]=cur;//Rebind front
                cur=curNext;
            }
        }
        array=newArray;
    }

    private double loadFactor(){
        return 1.0*usedSize/array.length;
    }

    /**
     * get function
     * Get the value of val according to the key
     * @param key
     * @return
     */
    public int get(int key){
        //1. Find the location of the key
        int index=key%this.array.length;
        //2. Get val
        Node cur=array[index];
        while (cur!=null){
            if (cur.key==key){
                return cur.val;
            }
            cur=cur.next;
        }
        return -1;
    }
}

Before capacity expansion:

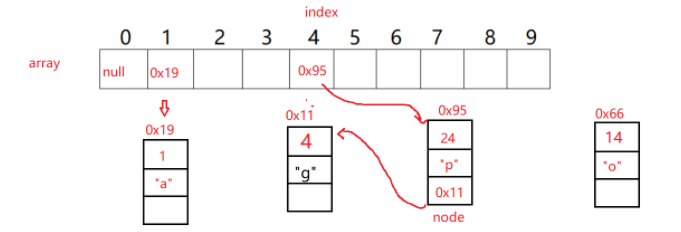
After capacity expansion: (re hash and then place elements)

4. Performance analysis

Although the hash table has been struggling with conflicts, in the actual use process, we think that the conflict rate of the hash table is not high, and the number of conflicts is controllable, that is, the length of the linked list in each bucket is a constant. Therefore, in the general sense, we think that the insertion / deletion / lookup time complexity of the hash table is low
O(1) .

5. Relationship with Java class set (code list)

1. Hash Map and Hash Set are the maps and sets implemented in java using hash tables
2. The hash bucket method is used in java to resolve conflicts
3. After the length of the conflict linked list is greater than a certain threshold, java will turn the linked list into a search tree (red black tree)
4. Calculating the hash value in java is actually the hashCode method of the called class. Comparing the equality of keys is to call the equals method of keys. Therefore, if you want to use a custom class as the key of HashMap or the value of HashSet, you must override the hashCode and equals methods, and the hashCode must be consistent for objects with equal equals;
5. hashcode is the same, but equals is not necessarily the same!
6. equals, hashcode must be the same!

The codes are listed below:

import java.util.HashMap;
import java.util.Objects;

/**
 * Created with IntelliJ IDEA.
 * User: 12629
 * Date: 2022/2/22
 * Time: 21:32
 * Description:
 */
class Person { //Custom person class
    public String ID;

    public Person(String ID) {
        this.ID = ID;
    }


    @Override // Override the equals method
    public boolean equals(Object o) {
        if (this == o) return true;
        if (o == null || getClass() != o.getClass()) return false;
        Person person = (Person) o;
        return Objects.equals(ID, person.ID);
    }

    @Override //Override hashcode method
    public int hashCode() {
        return Objects.hash(ID);
    }

    @Override
    public String toString() {
        return "Person{" +
                "ID='" + ID + '\'' +
                '}';
    }
}
public class HashBuck2<K,V> {

    static class Node<K,V> {
        public K key;
        public V val;
        public Node<K,V> next;

        public Node(K key,V val) {
            this.val = val;
            this.key = key;
        }
    }

    public Node<K,V>[] array = (Node<K,V>[])new Node[10];
    public int usedSize;

    public void put(K key,V val) {
        int hash = key.hashCode();
        int index = hash % array.length;
        Node<K,V> cur = array[index];
        while (cur != null) {
            if(cur.key.equals(key)) {
                cur.val = val;//Update val value
                return;
            }
            cur = cur.next;
        }
        Node<K,V> node = new Node<>(key, val);
        node.next = array[index];
        array[index] = node;
        this.usedSize++;
    }

    public V get(K key) {
        int hash = key.hashCode();
        int index = hash % array.length;
        Node<K,V> cur = array[index];
        while (cur != null) {
            if(cur.key.equals(key)) {
                //Update val value
                return cur.val;
            }
            cur = cur.next;
        }
        return null;
    }

    public static void main(String[] args) {
        
        //We believe that two people with the same ID card are the same person 
        //This logic can be implemented by rewriting the hashcode and equals methods
        //After rewriting hashcode, if the ID of string type is the same, the generated integer is the same
        //It realizes the logic that two people with the same ID are the same person
        
        Person person1 = new Person("123");
        Person person2 = new Person("123");

        HashBuck2<Person,String> hashBuck2 = new HashBuck2<>();
        hashBuck2.put(person1,"love");

        System.out.println(hashBuck2.get(person2));
    }

    
}

Because person1 and person2 are the same person
So the val of get person2 is actually put into the love of person1

• over