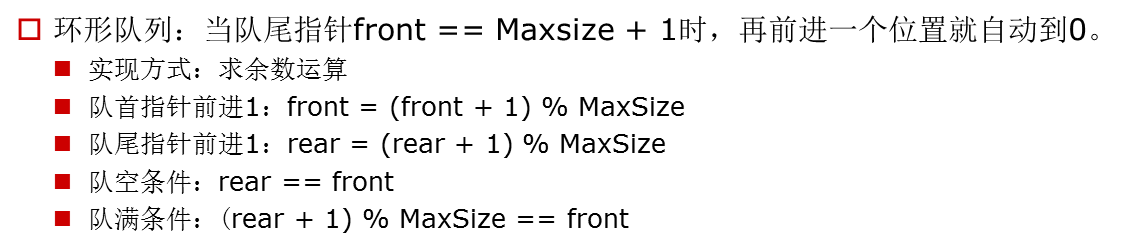Data Structure Foundation for Python

Posted by rachel2004 on Wed, 22 Apr 2020 19:27:53 +0200

1. Data Structure Basis

A. What is a data structure

        

b. Classification of data structures

       

c, List

        

import random
from timewrap import *

def list_to_buckets(li, iteration):
    """
    :param li: list
    :param iteration: Bucketing is the first iteration
    :return:
    """
    buckets = [[] for _ in range(10)]
    for num in li:
        digit = (num // (10 ** iteration)) % 10
        buckets[digit].append(num)
    return buckets

def buckets_to_list(buckets):
    return [num for bucket in buckets for num in bucket]
    # li = []
    # for bucket in buckets:
    #     for num in bucket:
    #         li.append(num)

@cal_time
def radix_sort(li):
    maxval = max(li) # 10000
    it = 0
    while 10 ** it <= maxval:
        li = buckets_to_list(list_to_buckets(li, it))
        it += 1
    return li

li = [random.randint(0,1000) for _ in range(100000)]
radix_sort(li)
list

d, Stack

                

 

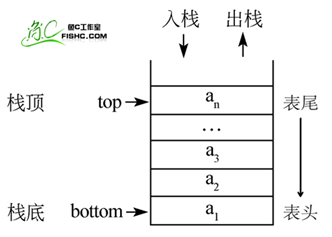
2. Python implementation of stack

 

a. Application of stack - topic of bracket matching

    

def brace_match(s):
    stack = []
    match = {')':'(', ']':'[', '}':'{'}
    match2 = {'(':')', '[':']', '{':'}'}
    for ch in s:
        if ch in {'(', '[', '{'}:
            stack.append(ch)
        elif len(stack) == 0:
            print("Lack%s" % match[ch])
            return False
        elif stack[-1] == match[ch]:
            stack.pop()
        else:
            print("Bracket mismatch")
            return False
    if len(stack) > 0:
        print("Lack%s" % (match2[stack[-1]]))
        return False
    return True


brace_match("[{()[]}{}{}")
Bracket Matching Implementation

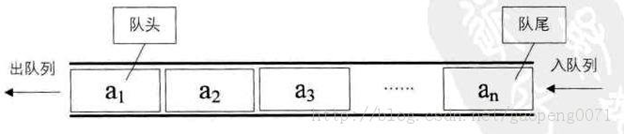
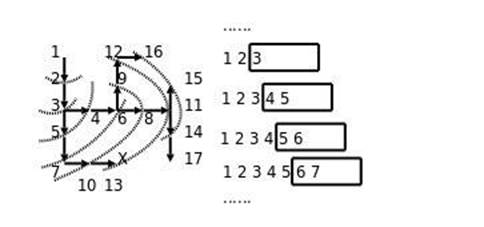
b. Queues

       

        

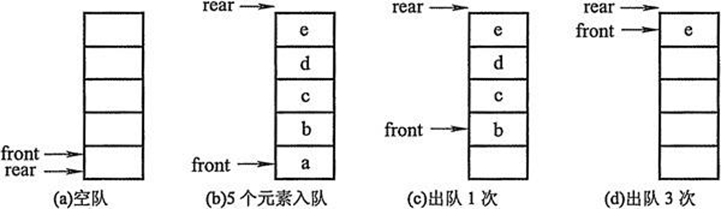
c. Implementation of queues

    

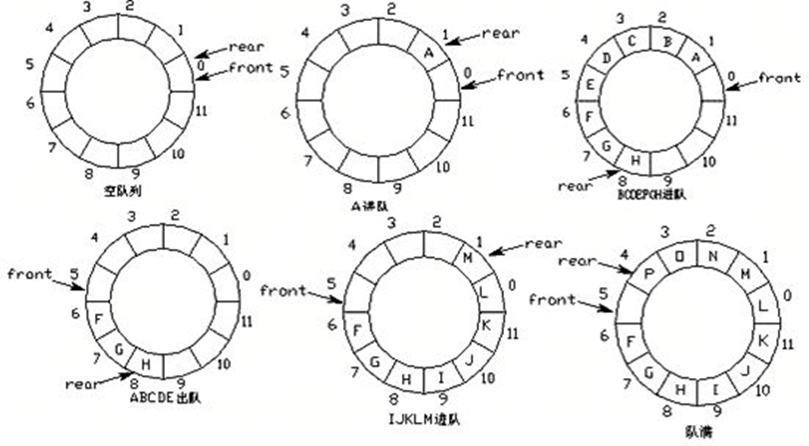
d. Implementation principle of queue--ring queue

 

e. Implementation principle of queue--ring queue

    

f, Queue's built-in modules

  

 

 

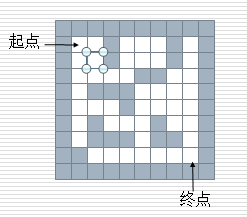
3. The Application of Stack--Maze as Topic

     

     

Solution ideas

from collections import deque

maze = [
    [1,1,1,1,1,1,1,1,1,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,0,0,1,1,0,0,1],
    [1,0,1,1,1,0,0,0,0,1],
    [1,0,0,0,1,0,0,0,0,1],
    [1,0,1,0,0,0,1,0,0,1],
    [1,0,1,1,1,0,1,1,0,1],
    [1,1,0,0,0,0,0,0,0,1],
    [1,1,1,1,1,1,1,1,1,1]
]

dirs = [
    lambda x,y:(x-1,y),  #upper
    lambda x,y:(x,y+1),  #right
    lambda x,y:(x+1,y),  #lower
    lambda x,y:(x,y-1),  #Left
]


def solve_maze(x1, y1, x2, y2):
    stack = []
    stack.append((x1,y1))
    maze[x1][y1] = 2
    while len(stack) > 0:   # Loop when stack is not empty
        cur_node = stack[-1]
        if cur_node == (x2,y2): #Arrive at End
            for p in stack:
                print(p)
            return True
        for dir in dirs:
            next_node = dir(*cur_node)
            if maze[next_node[0]][next_node[1]] == 0:   #Find a direction to go
                stack.append(next_node)
                maze[next_node[0]][next_node[1]] = 2  # 2 Represents a point that has passed
                break
        else: #If one direction is not found
            stack.pop()
    else:
        print("No way to go")
        return False






def solve_maze2(x1,y1,x2,y2):
    queue = deque()
    path = []    # Record nodes after queue
    queue.append((x1,y1,-1))
    maze[x1][y1] = 2
    while len(queue) > 0:
        cur_node = queue.popleft()
        path.append(cur_node)
        if cur_node[0] == x2 and cur_node[1] == y2:  #To End
            real_path = []
            x,y,i = path[-1]
            real_path.append((x,y))
            while i >= 0:
                node = path[i]
                real_path.append(node[0:2])
                i = node[2]
            real_path.reverse()
            for p in real_path:
                print(p)
            return True
        for dir in dirs:
            next_node = dir(cur_node[0], cur_node[1])
            if maze[next_node[0]][next_node[1]] == 0:
                queue.append((next_node[0], next_node[1], len(path)-1))
                maze[next_node[0]][next_node[1]] = 2 # Mark as past
    else:
        print("No way to go")
        return False




solve_maze2(1,1,8,8)
Labyrinth problem

a. Queue application

def solve_maze2(x1,y1,x2,y2):
    queue = deque()
    path = []    # Record nodes after queue
    queue.append((x1,y1,-1))
    maze[x1][y1] = 2
    while len(queue) > 0:
        cur_node = queue.popleft()
        path.append(cur_node)
        if cur_node[0] == x2 and cur_node[1] == y2:  #To End
            real_path = []
            x,y,i = path[-1]
            real_path.append((x,y))
            while i >= 0:
                node = path[i]
                real_path.append(node[0:2])
                i = node[2]
            real_path.reverse()
            for p in real_path:
                print(p)
            return True
        for dir in dirs:
            next_node = dir(cur_node[0], cur_node[1])
            if maze[next_node[0]][next_node[1]] == 0:
                queue.append((next_node[0], next_node[1], len(path)-1))
                maze[next_node[0]][next_node[1]] = 2 # Mark as past
    else:
        print("No way to go")
        return False




solve_maze2(1,1,8,8)
Labyrinth Problem - Queue Implementation

Chain List

 

 

import random
from timewrap import *

def list_to_buckets(li, iteration):
    """
    :param li: list
    :param iteration: Bucketing is the first iteration
    :return:
    """
    buckets = [[] for _ in range(10)]
    for num in li:
        digit = (num // (10 ** iteration)) % 10
        buckets[digit].append(num)
    return buckets

def buckets_to_list(buckets):
    return [num for bucket in buckets for num in bucket]
    # li = []
    # for bucket in buckets:
    #     for num in bucket:
    #         li.append(num)

@cal_time
def radix_sort(li):
    maxval = max(li) # 10000
    it = 0
    while 10 ** it <= maxval:
        li = buckets_to_list(list_to_buckets(li, it))
        it += 1
    return li

li = [random.randint(0,1000) for _ in range(100000)]
radix_sort(li)
list 

def insert_sort(li):
    for i in range(1, len(li)):
        # i Represents the first number of disordered zones
        tmp = li[i] # Touched cards
        j = i - 1 # j Point to the last position of the ordered region
        while li[j] > tmp and j >= 0:
            #Loop termination condition: 1. li[j] <= tmp; 2. j == -1
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp

def shell_sort(li):
    d = len(li) // 2
    while d > 0:
        for i in range(d, len(li)):
            tmp = li[i]
            j = i - d
            while li[j] > tmp and j >= 0:
                li[j+d] = li[j]
                j -= d
            li[j+d] = tmp
        d = d >> 1
Exercise i - Insert 
from timewrap import *

@cal_time
def binary_search(li, val):
    low = 0
    high = len(li) - 1
    while low <= high:
        mid = (low + high) // 2
        if li[mid] > val:
            high = mid - 1
        elif li[mid] < val:
            low = mid + 1
        else:
            return mid
    else:
        return -1

def find_a(nums, target):
    low = 0
    high = len(nums) - 1
    while low <= high:
        mid = (low + high) // 2
        if target <= nums[mid]:
            high = mid - 1
        else:
            low = mid + 1
    #[1, 2, 2, 2, 4, 8, 10]

    if low < len(nums):
        return low
    else:
        return -1



def find_b(nums, target):
    low = 0
    high = len(nums) - 1
    while low <= high:
        mid = (low + high) // 2
        if target < nums[mid]:
            high = mid - 1
        else:
            low = mid + 1
    if low < len(nums):
        return low
    else:
        return -1

@cal_time
def linear_search(li, val):
    try:
        return li.index(val)
    except ValueError:
        return -1

li = [1,2,2,2,4,8,10]
print(find_a(li, 10))
def insert_sort(li):
    for i in range(1, len(li)):
        # i Represents the first number of disordered zones
        tmp = li[i] # Touched cards
        j = i - 1 # j Point to the last position of the ordered region
        while li[j] > tmp and j >= 0:
            #Loop termination condition: 1. li[j] <= tmp; 2. j == -1
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp

def shell_sort(li):
    d = len(li) // 2
    while d > 0:
        for i in range(d, len(li)):
            tmp = li[i]
            j = i - d
            while li[j] > tmp and j >= 0:
                li[j+d] = li[j]
                j -= d
            li[j+d] = tmp
        d = d >> 1

Topics: Python Lambda

Hot Topics

©2024 Programmer Think