chart
In mathematics, a graph is a structure described in a group of objects, some of which are "related" in a sense. These objects correspond to mathematical abstractions called vertices (also known as nodes or points), and each associated vertex pair is called an edge (also known as a link or line). Usually, a graph is depicted diagrammatically as a set of points or rings of vertices connected by lines or curves of edges. Graph is one of the research objects of discrete mathematics------ Baidu Encyclopedia
6.1 basic terms
Figure: marked as G = (V, E)
Where: V is the vertex set of G, which is a finite non empty set;
E is the edge set of G and is a finite set
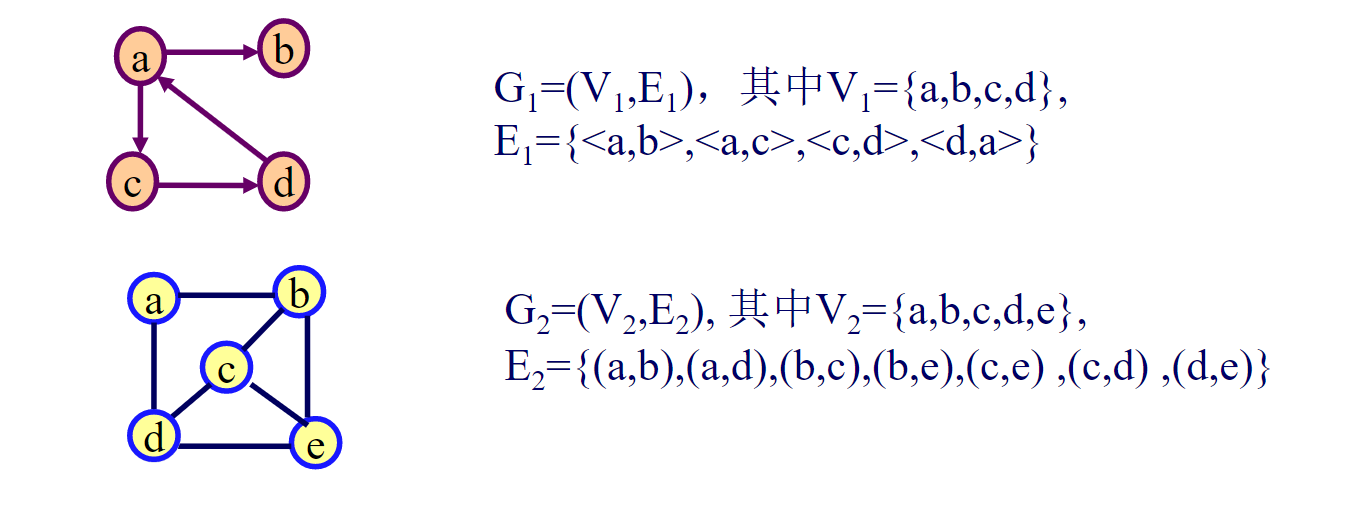



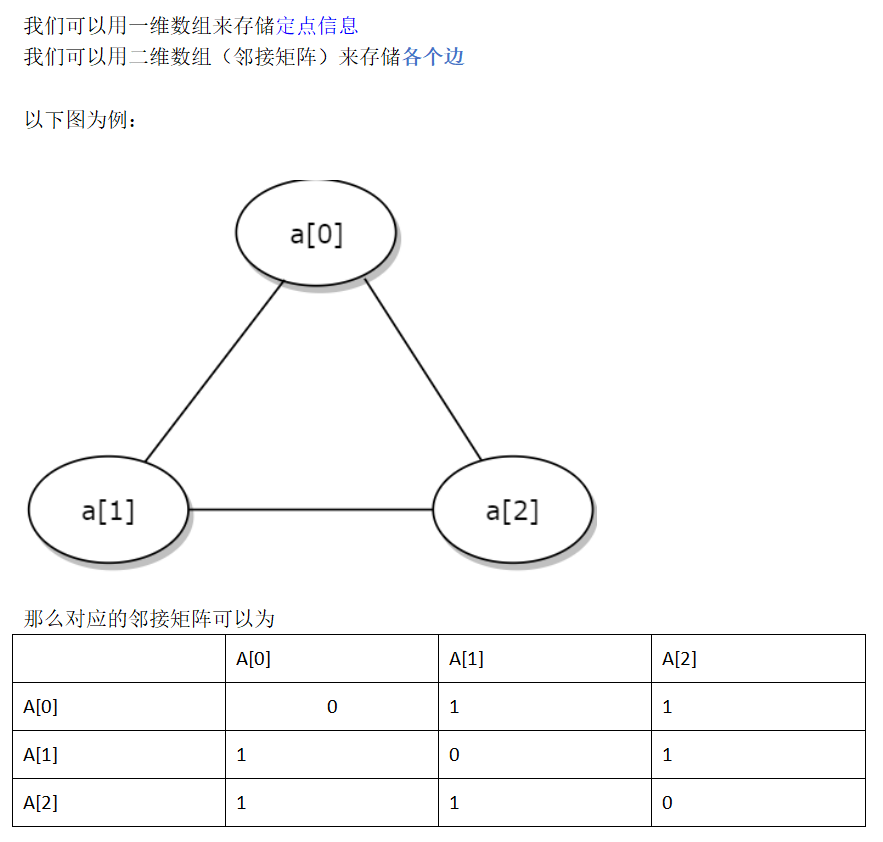
6.2 storage structure
- Figure features: nonlinear structure
- Sequential storage structure of graph: none (multiple fixed points, out of order), but array can be used to describe the relationship between elements. (designed as adjacency matrix)
- Linked storage structure: multiple linked lists (adjacency list, adjacency multiple list, cross linked list) can be used
The following conclusion surface introduces the array representation (adjacency matrix) and chain representation (adjacency table) of graphs
Array representation of graphs (adjacency matrix as an example)
Directly give the storage structure code
#define MAX_ VERTEX_ Num 100 / * the maximum number of vertices is set to 100*/
/*---Adjacency matrix representation of Graphs---*/
typedef struct
{
int vexs[MAX_VERTEX_NUM]; /*Vertex vector*/
int arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; /*Adjacency matrix*/
int vexnum,arcnum; /*Number of vertices and edges*/
int kind; /*---Type of graph (1: directed graph 0: undirected graph)---*/
}Mgraph;
explain
The matrix representation of edges is given
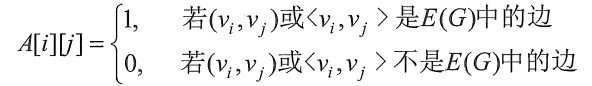

Remembering the above rules is very helpful for the creation of directed and undirected graphs
Chain storage structure of graph (adjacency list as an example)
/*-------------- Adjacency table of graph--------*/
#define MAX_VERTEX_NUM 100
typedef struct ArcNode{
int adjvex; //The vertex position to which the arc points
struct ArcNode *nextarc; //Pointer to the next arc
int weight;
}ArcNode; //Table node (Fox)
typedef struct VNode{
int data; //Vertex information
ArcNode *firstarc; //Pointer to the first arc attached to the vertex
}VNode; //vertex
typedef struct {
Vnode adjlist [MAX_VERTEX_NUM]; /*Adjacency table*/
int vexnum,arcnum; //Number of vertices, number of edges
int kind;
}ALGraph; //Adjacency table of graph
explain


6.3 graph traversal
Traversal definition: starting from a given vertex in the graph, visiting all vertices in the graph along some edges, and making each vertex accessed only once is called traversal of the graph.
Traversal essence: the process of finding the adjacency point of each vertex.
Characteristics of graph: there may be loops in the graph, and any vertex of the graph may be connected with other vertices. After accessing a vertex, it may return to the visited vertex along some edges.
Solution: you can set an auxiliary array visited [n] to mark each accessed vertex. Its initial state is 0. During the traversal of the graph, once a vertex I is accessed, it is immediately changed to visited [i] to 1 to prevent it from being accessed multiple times.
Common traversal methods of graph: 1. Depth first search 2. Breadth first search
Depth first traversal of Graphs
Depth first search is also called depth first search, or DFS for short.
Its principle is as follows:
- After accessing a starting vertex v in the graph, start from V and access any adjacent vertex w1;
- Then, starting from w1, access the vertex w2 adjacent to w1 but not yet accessed;
- Then start from w2 and make a similar visit
- This continues until you reach the vertex u where all adjacent vertices have been visited.
- Then, go back to the vertex you just visited last time to see if there are other adjacent vertices that have not been visited.
- If yes, access this vertex, and then start from this vertex to access similar to the above;
- If not, go back and search. Repeat the above process until all vertices in the connected graph have been accessed
[external chain picture transfer failed. The source station may have anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-wjv3zenw-163672246012)( https://img2020.cnblogs.com/blog/2190843/202111/2190843-20211112202027103-1151409099.gif )]
[external chain picture transfer failed. The source station may have anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-iuycausj-163672246012)( https://img2020.cnblogs.com/blog/2190843/202111/2190843-20211112203741798-1811882883.gif )]
Note: the drawing is not good. You'd better understand the text slowly
It is not difficult to see from the text that this is a recursive idea.
Given code (adjacency matrix):
void DFS( Mgraph g,int v,int visited[])
{/* The adjacency matrix is stored, and the depth first search is carried out for graph g from vertex v*/
int j;
printf("%d ",g.vexs[v]);
visited[v]=1; /*Identity v accessed*/
for(j=0;j<g.vexnum;j++); /* */
{
if( g.arcs[v][j]==1&&visited[j]==0)/*j Is the adjacency point of v, which has not been accessed*/
DFS(g,j,visited); /*Calling DFS recursively from j*/
}/*for*/
}/*DFS*/
void DFSTraverse(Mgraph g)
{ /*Adjacency matrix depth first search*/
int v;
int visited[MAX_VERTEX_NUM];
for(v=0;v<g.vexnum;v++)
visited[v]=0; /*Initialize visited array*/
for(v=0;v<g.vexnum;v++)
if(visited[v]==0) DFS(g,v,visited);
/*Never visited, DFS search*/
}
Given code (adjacency table):
void DFS(ALGraph *g,int v,int visited[])
{/*Starting from vertex v, depth first search is performed on graph g*/
ArcNode *p;
int w;
printf("%d ",g->adjlist[v].data);
visited[v]=1; /*Identity v accessed*/
p=g->adjlist[v].firstarc; /*p Pointer to the header of the v-th single linked list*/
while(p)
{
w=p->adjvex; /*w Adjacency point of v*/
if(visited[w]==0) /*If w is not accessed*/
DFS(g,w,visited); /*Calling DFS recursively from w*/
p=p->nextarc; /*Find the next adjacent contact of v*/
}/*while*/
}/*DFS*/
void DFSTraverse(ALGraph *g)
{ /*Adjacency table depth first search*/
int v;
int visited[MAX_VERTEX_NUM];
for(v=0;v<g->vexnum;v++)
visited[v]=0; /*Initialize visited array*/
for(v=0;v<g->vexnum;v++)
if(visited[v]==0) DFS(g,v,visited);
/*Never visited, DFS search*/
}
Performance analysis of DFS algorithm
DFS algorithm is a recursive algorithm, which needs the help of a recursive work stack, so its spatial complexity is O (V) O (V) O (V).
For a graph with n vertices and e edges, the adjacency matrix is a two-dimensional array. To find the adjacency point of each vertex, you need to access all elements in the matrix, so it takes O (V 2) O (V ^ 2) O (V 2) time. When the adjacency table is used as the storage structure, the time required to find adjacency points depends on the number of vertices and edges, so it is O (V + e) O (V + e) O (V + e). Obviously, for sparse graphs with few points and polygons, the adjacency table structure greatly improves the time efficiency of the algorithm.
For a directed graph, because it is only feasible or infeasible for the channel, there is no change in the algorithm, and it is completely universal.
Breadth first traversal of Graphs
Breadth first search, also known as breadth first search, is called BFS for short.
Basic idea: -- the hierarchical traversal process of imitation tree.
Traversal steps: after accessing the starting point v, access the adjacent points of V in turn; Then, the adjacent points in these points (the next layer) that have not been accessed are accessed successively (sequentially); Until all vertices have been accessed.
Breadth first search is a hierarchical search process. Each step forward may access a batch of vertices, unlike the fallback of depth first search.
Therefore, breadth first search is not a recursive process, and its algorithm is not recursive
Given code (adjacency matrix):
void BFSTraverse(Mgraph *mgraph, int n)
{
int v,w,u;
int visited[n];
int Q[n+1],r,f; //Q is the queue, where r and f are the end of the queue pointer and the end of the queue pointer respectively
//Initializing visited arrays and queues
int i;
for(i = 0;i<n;i++)
{
visited[i] = 0;
}
f = 0;
r = 0;
for(v = 0;v< mgraph->vexnum;v++)
{
if(!visited[v])
{
visited[v] = 1;//Default access from v = 0 (first access)
printf("%d ",mgraph->vexs[v]);//Print
Q[r] = v;//Queue
r = (r+1)%(n+1);
while(f<r) //When the queue is not empty
{
u = Q[f];f = (f+1)%(n+1);//Queue out and assign the number of queues to u
for(w = 0;w<mgraph->vexnum;w++)
{
if(mgraph->arcs[u][w]==1 && visited[w] == 0) //Traverse all the adjacency points of the vertex to find whether there are adjacency points that have not been visited
{//Find and output and join the team
visited[w] = 1;
printf("%d ",mgraph->vexs[w]);
Q[r] = w;r = (r+1)%(n+1);
}
}
}
}
}
}
Given code (adjacency table):
void BFSTraverse(ALGraph *g ,int n)
{
int v,w,u;
int Q[n+1];
int visited[g->vexnum];
int r = 0 ,f = 0;
ArcNode *p;
for(int i = 0;i<n+1;i++) Q[i] = 0;
for(v=0;v<g->vexnum;v++) visited[v]=0 ;//Initialize visited array
//Queue Q initialization
for(v=0;v<g->vexnum ;v++) //Breadth first search from v
{ if (!visited[v])
{
visited[v]=1;
printf("%d ",v); //Output v
Q[r] = v; r = (r+1)%(n+1); //v join the team
while(f<r || f>r) //Queue Q is not empty
{
u = Q[f]; f = (f+1)%(n+1);// u out of the team
p=g->adjlist[u].firstarc ;
while(p) //Access the adjacency points of u in turn
{ w=p->adjvex;
if(!visited[w])
{ visited[w]=1;
printf("%d ",w);
Q[r] = w; r = (r+1)%(n+1); //w join the team
}
p=p->nextarc ; //p points to the next adjacent contact
}//end of while
}//end of while
}//end of if
}//end of for
}//end of BFSTravers