1. Hash table

Why is there a hash table?

For example, chestnuts:

There are thousands of employees in a company. How do I find an employee's information

Through the array, each employee corresponds to a job number. I can directly find the job number to obtain the corresponding information

But I don't want to get it through the job number. I want to get it through the employee's name. At this time, I will think of the linked list, but the problem comes. The linked list is an information linked to one information, and the efficiency is very slow

At this time, the hash table can be used. The name of each employee can be converted into a corresponding number, and the number corresponds to the name. In this way, I can obtain the employee information directly through the number

1.1 hashing

The process of converting large numbers into subscripts within the array range (the range here is defined by itself). For example, 0-100 takes the remainder 10 to get the subscript value of 0-9 (there are many ways, such as bit operation in java). This process is called hashing

If there are 5000 words, an array with a length of 5000 may be defined, but in practice, we can't guarantee that the large numbers corresponding to these words are completely different, so we need to double the size of 10000. Although the length of the array is enough, the index after hashing may still be repeated, At this time, it is necessary to resolve conflicts (conflicts here refer to the hash of large numbers, not large numbers)

1.2 hash function

Usually, we will convert words into large numbers (power multiplication). The code of large numbers after hashing will be processed by a function to get the desired data. This function is the hash function

Why convert words into large numbers: because we need to convert the corresponding words into a very large number in an appropriate way, so that they will not be repeated with other words, ensuring that each word has a corresponding number (but if the data is too large, it needs to be hashed)

1.3 hash table

Finally, the data is inserted into an array, which is called a hash table

1.4 conflict resolution

• What is conflict? Conflict means that there will be the same subscript value after hashing. There are two ways to solve conflict: chain address method and development address method

• Chain address method

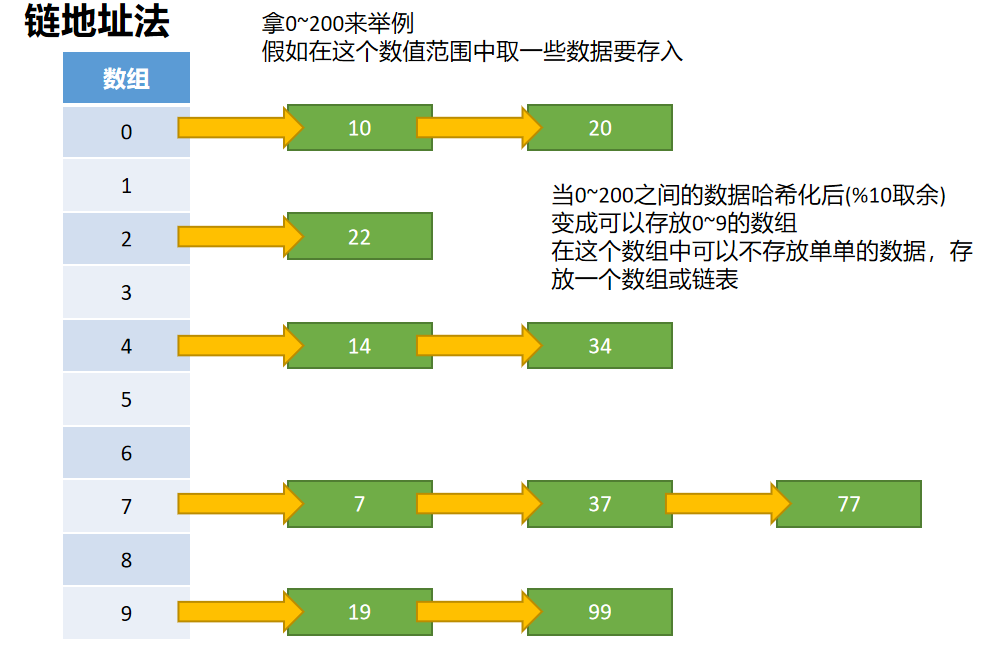
• The solution to the conflict of chain address method is that the data stored in each array is no longer a single data, but a linked list or array

• When querying, first find the corresponding position according to the hashed subscript, and then perform linear search in the corresponding position

• The problem is whether to select a linked list or an array. In fact, they are almost the same, because there are few conflicts (but we need to solve them), which means that the length of the linked list or array behind it will not be very long. They are all linear checks, and the efficiency is not much worse

• The choice of linked list or array depends on the demand. Both linked list and array have their own advantages and disadvantages. Array is suitable for inspection and modification, and linked list is suitable for insertion and deletion

• Open address method

• Developing the address method is to find a blank location to store conflicting data, because after processing, the length of the storage array is enough to store these data (if the length is not enough, it will expand), but there will be conflicts after hashing. The efficiency of developing the address method is higher than that of the chain address method. There are three ways to develop the address method, linear detection Secondary detection, re Hashimoto

• Linear detection

  Insert: suppose that there is a data of 22 in the subscript 2, and then I want to insert the data of 32. At this time, linear detection is required. Linear detection is to check the blank unit linearly. If there is no content in the subscript 3, you can use line detection to make index + + (currently refers to 2). When it is added to 3, 32 is inserted, Linear detection will only start from the corresponding subscript, not from scratch

  Query: the idea of query is the same as that of insertion. If there are values 62, 72, etc., there is also the idea of querying the value of index=2. For example, I want to check whether there is 102. Linear search stops when an empty position has not been found, because all empty positions will be excluded when inserting. All empty positions have been found and have not been found, It can already indicate that there is no such value

  Delete: the same idea applies to deletion and query insertion. However, it should be noted that after deletion, the content of this subscript cannot be set to null, because if it is set to null, an empty item will be found during query insertion and deletion, so it will not be detected backward. Then, it will not be found when I save 62 and 72, Therefore, after deletion, special processing needs to be done (for example, set to - 1), indicating that it is deleted, and there may be the same type behind it (here, the type refers to 2 at the end, which can be distinguished after hashing), and then it can be placed at this - 1 position when inserting again

  Linear detection: a serious problem with linear detection is aggregation. For example, when we do not have any data, we insert some data 22-23-24-25-26-27, which means that there are elements at the position of 2-3-4-5-6-7. This series of data is called aggregation. Aggregation will affect the performance of hash table, whether it is insertion, deletion or query, For example, if we insert a 32, we will find that there is data from 2-7, but it will still detect bit by bit, which is particularly performance consuming. At this time, we need secondary detection. Secondary detection can solve some of this problem

• Secondary detection

  Secondary detection is actually an improved version of linear detection: linear detection is x+1, x+2 and x+3 step by step, while secondary detection is x+1 (square), x+2 (square) and x+3 (square). Other operations are the same as linear detection, that is, the step size is different

  The problem of secondary detection: if we insert the data of 32-112-42-92-2, this situation will also cause a focus with different steps. At this time, we need Hashi method to fundamentally solve the problem

• double hashing

  Re hashing method: linear detection and secondary detection will have corresponding focusing problems. In order to solve these problems, it is necessary to use hashing method. Re hashing method detects according to keywords. Even if different keywords are mapped to the same array subscript (conflict), different detection sequences (steps) can be used, and different steps can be used for different keywords, Unlike the first hash function, the second hash function cannot output 0, because the output of 0 means that there is no step size, and the algorithm enters an endless loop

  New hash function: stepsize = constant - (key% constant), where key is the length of the data, constant is a prime number, and is less than the capacity of the array. For example, stepsize = 5 - (key% 5), the result can not be 0 in any case

1.5 efficiency of hashing

• If there is no conflict, the efficiency will be very high
• In case of conflict, the access time depends on the subsequent detection length. The average detection length and average access time depend on the loading factor. As the loading factor becomes larger, the detection length becomes longer and longer
• Loading factor = total data item / hash table length
• The loading factor of open address method can only be 1 at most, because it must find a blank cell to put elements into
• The loading factor of chain address method can be greater than 1, because the zipper of chain address method can extend indefinitely (the efficiency is getting lower and lower at the back)

1.6 excellent hash function

• Fast calculation

  • Using multiplication in a computer is very performance consuming

  • To convert the corresponding data to a large number, we use the power multiplication. Here, we will use a lot of multiplication, such as

    cats = 3 * 27^3 + 1*27^2 + 20 * 27^1 + 17 * 27^0 = 60337

    Note: 27 is the base of the power selected by yourself, ^ represents the power, and 3, 1, 20 and 17 represent the code of the corresponding word

    Each word is converted in this way, which can be represented by N. after a series of simplification operations, the multiplication times become n(n+1)/2 times, and the addition times are n times

  • Horner's rule: in order to solve this kind of evaluation problem, Horner's rule is also called Qin Jiushao algorithm in China

    After the change of Horner's law, the number of multiplication is n times and the number of addition is n times

    If large o is used to represent time complexity, it is directly reduced from O(N^2) to O(N)

• Uniform distribution

  • In hash table, whether chain address method or open address method, when multiple elements are mapped to the same location, it will affect the efficiency

  • Therefore, an excellent hash function should map elements to different locations as much as possible when elements are evenly distributed in the hash table

  • For uniform distribution, try to use prime numbers when using constants

    The length of the hash table and the base of the power all use prime numbers. In order to make the hash table more evenly distributed, hashing method is also easier to find

    For example, chestnuts:

    If the container length is 15 (subscript value 0 ~ 14), calculate the step to be found through the function of rehash method: 5 - (15% 5) = 5 (step)

    Detection sequence: 0 - 5 - 10 - 0 - 5 - 10... If there is data in 0, 5 and 10, the program will become an endless loop

    If the container length is 13 (subscript value 0 ~ 12), the search step is 5 - (13% 5) = 2 (step)

    Detection sequence: 0 - 2 - 4 - 6 - 8 - 10 - 12 - 1 - 3 - 5 - 7 - 9 - 11. Every position will be detected

    When trying one, the container length is 7 (subscript value 0 ~ 6), and the search step is 5 - (7% 5) = 3 (step)

    Detection sequence: 0 - 3 - 6 - 2 - 5 - 1 - 4. Each position will also be detected

    In this way, not only will there be no loop, but also the data can be more evenly distributed in the hash table (mathematical knowledge is designed in this)

1.7 hash table expansion

• In the chain address method, the loading factor can be greater than 1
• However, as the amount of data increases, the bucket corresponding to each index will become longer and longer, which will reduce the efficiency
• Therefore, it is necessary to expand the capacity of the array at this time
• It is common to expand the capacity when the loading factor is > 0.75, and the expansion efficiency is the highest at this time
• After capacity expansion, empty the data in the previous array and add it to the new array again
• With capacity expansion, of course, there will be corresponding capacity reduction. The implementation principle of capacity reduction is actually the same as that of capacity expansion
• Shrink the volume when the filling factor is < 0.25
• Because if there is no capacity reduction and only capacity expansion, I always add data, and then the array will continue to expand, and then I always delete data. At this time, there will be many empty positions in the array, wasting a lot of unnecessary space, so I also need to use capacity reduction

1.8 hash table encapsulation (chain address method)

• hash function

  // Encapsulate hash function
  // str: data to be converted to a large number
  // size: the length of the array
  function hashFn(str, size) {
    // Store large numbers
    let hashCode = 0
  
    // Horner's Law: efficient computing
    // ((...(((anx + an - 1)x + an - 2)x + an - 3)...)x + a1)x + a0
    for (let i = 0; i < str.length; i++) {
      // Charcodeat -- > to Unicode encoding
      // 37 the prime number you choose is more than 37
      hashCode = hashCode * 37 + str.charCodeAt(i)
    }
  
    // The length of the array is modular (hashed), which is convenient for storing different corresponding positions
    let index = hashCode % size
    return index
  }
  

• Efficient judgment of prime numbers

  function isPrime(num) {
    // Sqrt (n) -- > refers to the square root of n
    // If a number n can be factorized, the two numbers obtained by factorization
    // There must be one less than or equal to sqrt(n) and one greater than or equal to sqrt(n)
    let temp = parseInt(Math.sqrt(num))
    
    for (let i = 2; i <= temp; i++) {
      if (num % i == 0) {
        return false
      }
    }
    return true
  }
  

• Hashtable

  // The addition, deletion, modification and query of hash table are the same
  // 1. Take out the corresponding subscript through hash function conversion, that is, the bucket of data to be stored
  // 2. Check whether the bucket is empty
  //  (1) In the addition operation, if the bucket is empty, create a bucket (array is used here, and the efficiency of array and linked list is similar)
  //  (2) In the hash table, adding and modifying are the same method, because the key is used to add or modify data,
  //      Adding without a key is equivalent to adding, and modifying value with a key is equivalent to modifying
  //  (3) In query and deletion, if there is no bucket, the operation corresponding to the operation failure is returned
  // 3. Traverse the bucket and add, delete, modify and query. The second point refers to the bucket, and the third point refers to the data in the bucket. The ideas are the same
  // 4. Add and delete operations that only exist
  //  (1) Add, add 1 to the content length, and then check whether it needs to be expanded
  //  (2) Delete, the content length is reduced by 1, and delete to see whether it needs to shrink
  //  (3) After capacity expansion or reduction, the data must also be prime
  
  // Hash table class
  class HashTable {
    constructor() {
      // Outermost large array (hash table)
      this.storage = []
      // Data volume (total length of data content)
      this.count = 0
      // Hash table length
      this.limit = 7
    }
  
    // Encapsulate hash function
    // str: data to be converted to a large number
    // size: the length of the array
    hashFn(str, size) {
      // Store large numbers
      let hashCode = 0
  
      // Horner's Law: efficient computing
      // ((...(((anx + an - 1)x + an - 2)x + an - 3)...)x + a1)x + a0
      for (let i = 0; i < str.length; i++) {
        // Charcodeat -- > to Unicode encoding
        // 37 the prime number you choose is more than 37
        hashCode = hashCode * 37 + str.charCodeAt(i)
      }
  
      // The length of the array is modular (hashed), which is convenient for storing different corresponding positions
      let index = hashCode % size
      return index
    }
  
    // 1.put(key, value): insert and modify data
    put(key, value) {
      // Take out the corresponding subscript to be put in
      let index = this.hashFn(key, this.limit)
  
      // Bucket: because of the selected chain address method, each corresponding subscript must store an array (bucket)
      let bucket = this.storage[index]
  
      // If the bucket does not exist, it indicates the first insertion value. You need to create the bucket and place it at the corresponding subscript position
      if (bucket == null) {
        bucket = []
        this.storage[index] = bucket
      }
  
      // If the data is added for the first time, the loop will not come in (bucket.length == 0)
      for (let i = 0; i < bucket.length; i++) {
        // Each item of data is also stored in an array, [key, value]
        let data = bucket[i]
        // If the same key is found, modify it
        if (data[0] == key) {
          data[1] = value
          return
        }
      }
      // Add without
      bucket.push([key, value])
  
      // Add data content plus one
      this.count++
      // When the loading factor is > 0.75, expand the capacity of the array hash table
      if (this.count > this.limit * 0.75) {
        // Check whether this number is a prime number. If yes, it will return and if not, it will become a prime number
        let prime = this.setPrime(this.limit * 2)
        this.resize(prime)
      }
    }
  
    // 2.get(key): get data
    get(key) {
      // Take out the corresponding subscript to find
      let index = this.hashFn(key, this.limit)
  
      // Remove the current bucket
      let bucket = this.storage[index]
  
      // If the bucket is empty, return directly
      if (bucket == null) {
        console.log("The bucket is empty");
        return
      }
  
      for (let i = 0; i < bucket.length; i++) {
        let data = bucket[i]
        // Find the key equal and return value
        if (data[0] == key) {
          return data[1]
        }
      }
  
      return "There is no such data"
    }
  
    // 3.remove(key): delete data and return it
    remove(key) {
      let index = this.hashFn(key, this.limit)
  
      let bucket = this.storage[index]
  
      if (bucket == null) {
        console.log("The bucket is empty");
        return
      }
  
      for (let i = 0; i < bucket.length; i++) {
        let data = bucket[i]
        if (data[0] == key) {
          // Delete the current item when it matches
          bucket.splice(i, 1)
          this.count--
  
          // The minimum hash table length is 7 (because it is too small and unnecessary)
          // When the filling factor is < 0.25, the volume is reduced
          if (this.limit > 7 && this.count < this.limit * 0.25) {
            let prime = this.setPrime(Math.floor(this.limit / 2))
            this.resize(prime)
          }
  
          return data[1]
        }
      }
      return "There is no such data"
    }
  
    // 4.isEmpty(): check whether the hash table is empty, return true if it is empty, and return false if it is not empty
    isEmpty() {
      return this.count == 0
    }
  
    // 5.size(): get the number of elements in the hash table
    size() {
      return this.count
    }
  
    // resize(newLimit): hash table capacity expansion / reduction
    resize(newLimit) {
      // Save the original data first
      let oldStorage = this.storage
  
      // Initialize and then change the hash table length
      this.storage = []
      this.count = 0
      this.limit = newLimit
  
      // 
      for (let i = 0; i < oldStorage.length; i++) {
        let bucket = oldStorage[i]
  
        // Skip if empty
        if (bucket == null) {
          continue
        }
  
        // If there are any values, they are all added to the new hash table length
        for (let i = 0; i < bucket.length; i++) {
          let data = bucket[i]
          this.put(data[0], data[1])
        }
      }
    }
  
    // isPrime(num): determines whether a number is a prime number. It is true, not false
    isPrime(num) {
      // Sqrt (n) -- > refers to the square root of n
      // If a number n can be factorized, the two numbers obtained by factorization
      // There must be one less than or equal to sqrt(n) and one greater than or equal to sqrt(n)
      let temp = parseInt(Math.sqrt(num))
      
      for (let i = 2; i <= temp; i++) {
        if (num % i == 0) {
          return false
        }
      }
      return true
    }
  
    // setPrime(num): change a number to a prime number
    setPrime(num) {
      while (!this.isPrime(num)) {
        num++
      }
      return num
    }
  }
  
  // test
  let hashTable = new HashTable()
  
  hashTable.put("Xiao Hong", "1")
  hashTable.put("Xiaobai", "12")
  hashTable.put("Blue ", "123")
  hashTable.put("Little green", "1234")
  hashTable.put("Xiao Hei", "12345")
  hashTable.put("Xiaotian", "123456")
  hashTable.put("Xiao Huang", "1234567")
  
  // console.log(hashTable.get("big dog");
  // hashTable.get("little black")
  
  console.log(hashTable.remove("Xiao Hong"));
  console.log(hashTable.remove("Xiaobai"));
  console.log(hashTable.remove("Little green"));
  console.log(hashTable.remove("Xiao Hei"));
  
  // console.log(hashTable.isEmpty());
  
  // console.log(hashTable.size());
  
  console.log(hashTable);