Heap

• Heap is a special kind of data structure in computer science. Heap can usually be regarded as an array object of a complete binary tree.
• Heap classification: the heap with the largest root node is called the maximum heap or large top heap, and vice versa is called the minimum heap or small top heap. Common heaps include binary tree heaps, Fibonacci heaps, etc.

Characteristics of reactor

1. Each node can have at most two nodes.
2. Except that the root node has no siblings, the last left child node can have no siblings, and other nodes must have siblings.
3. The key value of the root node is the largest (smallest) of all heap nodes, and the value of each node is larger (smaller) than that of its child node

As shown in figure A,B is not a heap, and C is the largest heap.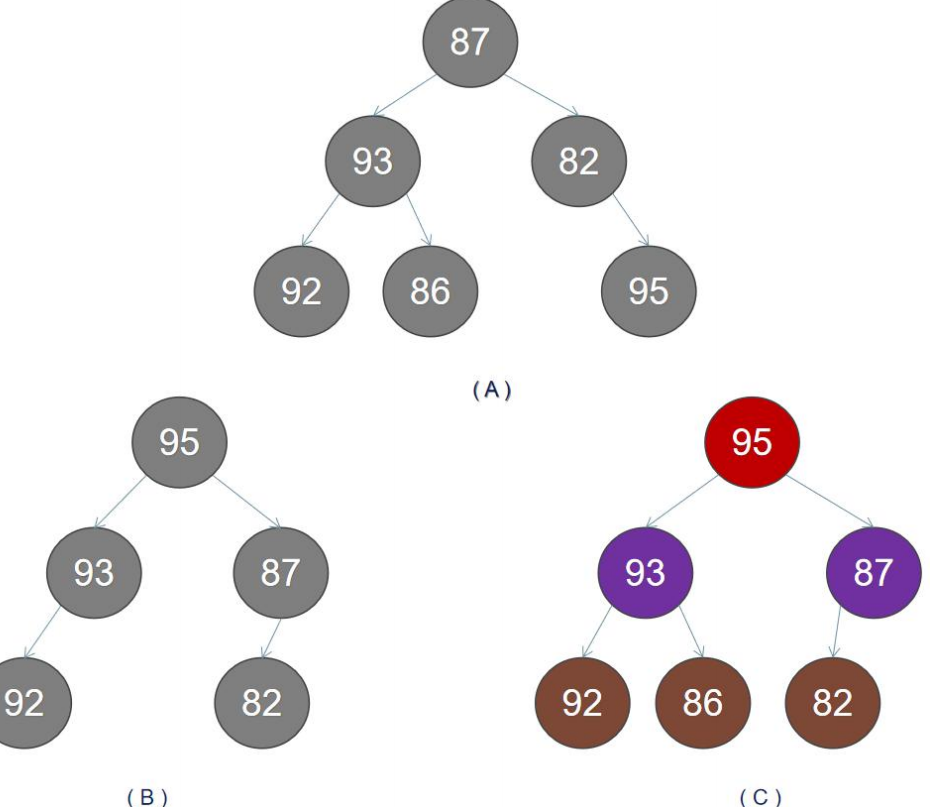

Algorithm implementation of heap (taking the maximum heap as an example)
Build the following array as the maximum heap

1. First, we need to find the parent node of the last node, as shown in figure (a). The node we find is 87, and then find the largest child node of the node to compare with ourselves. If the child node is larger than itself, the two nodes will be exchanged.
   In figure (a), 87 is smaller than the left child node 95, so after exchange, it is shown in figure (b).
   
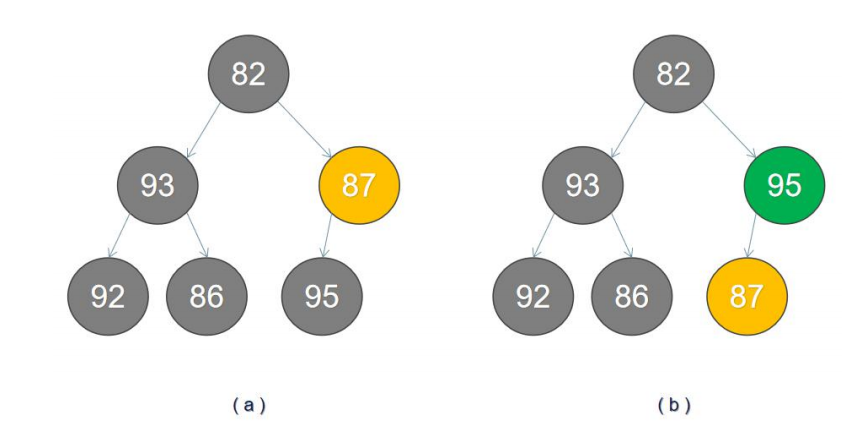
   2. We move to the previous parent node 93. Similarly, we do the comparison operation in the first step. The results do not need to be exchanged
   3. Continue to move the node to the previous parent node 82, as shown in figure (d). 82 is smaller than its two nodes, but its right child node is larger than its left child node, so 82 and 95 are exchanged, as shown in figure (e). After 82 is exchanged, its value is smaller than the left child node, which does not meet the characteristics of the maximum heap, so continue to adjust downward, as shown in figure (f)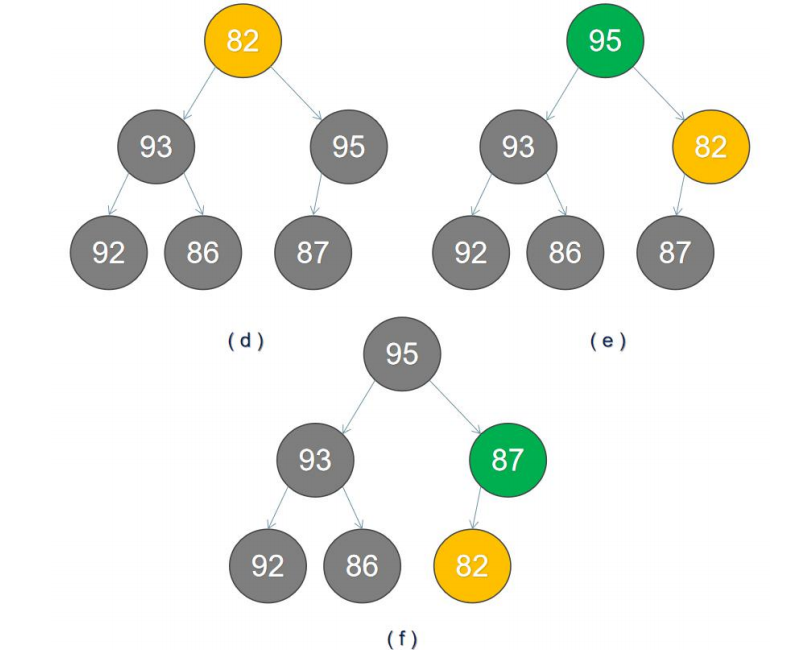
   Build heap

#define DEFAULT_CAPCITY 128 
typedef struct _Heap{ 
 int *arr; //An array that stores heap elements
 int size;//Number of elements currently stored
 int capacity; //Current storage capacity 
}Heap;

/*Adjust the current node and child nodes to the maximum heap*/
 void adjustDown(Heap &heap, int index) 
 {
   int cur=heap.arr[index];//Current node to be adjusted
   int parent,child; 
   /*Judge whether there is a sub node larger than the current node. If it does not exist, the heap itself is balanced and does not need to be adjusted; If it exists, exchange the largest child node with it. After the exchange, if the child node has children, continue to adjust the child node according to the same steps*/ 
   for(parent=index; (parent*2+1)<heap.size; parent=child)
   { 
      child=parent*2+1; //Take the largest of the two child nodes 
      if(((child+1)<heap.size)&&(heap.arr[child]<heap.arr[child+1]))
        {
         child++; 
         }
   //Judge whether the largest node is larger than the current parent node 
     if(cur>=heap.arr[child])
       {
          //No more than, no adjustment is required and the loop is skipped
           break; 
       }else {
       //Greater than the current parent node, swap, and then continue to adjust downward from the child node position 
              heap.arr[parent]=heap.arr[child];
               heap.arr[child]=cur; 
               }
   }
 }



/* From the last parent node (size/2-1's location), adjust all parent nodes (until the root node) one by one, ensure that every parent node is a maximum heap, and finally form a maximum heap on the whole. */ 
  void buildHeap(Heap &heap)
    { 
      int i;
      for(i=heap.size/2-1; i>=0; i--)
        { 
          adjustDown(heap, i); 
        } 
     }

Insert the number 99 into the upper large top pile
1) The original heap is shown in the figure: corresponding array: {95,, 93,, 87,, 92,, 86,, 82}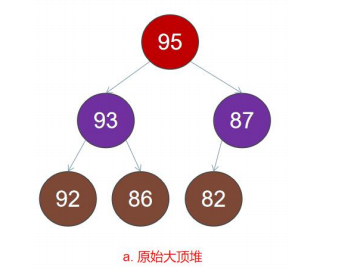
2) Insert the new element into the tail of the big top heap, as shown in Figure b: the corresponding array is: {95,, 93,, 87,, 92,, 86,, 82, 99}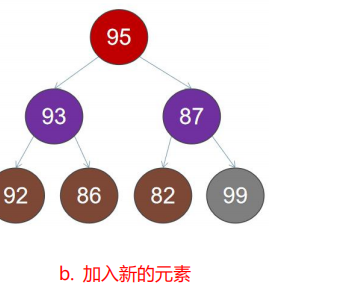
3) At this time, the maximum heap has been destroyed and needs to be readjusted. Since the added node is larger than the parent node, the new node can be exchanged with the parent node, as shown in Figure c; After adjustment, if the new node is smaller than the new parent node, it has been adjusted in place. If it is larger than the new parent node, it needs to be exchanged with the parent node again, as shown in Figure d. so far, the maximum heap adjustment is completed.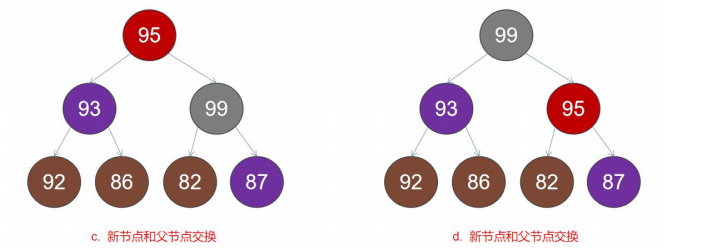

/*Adjust the current node and parent node to the maximum heap*/
 void adjustUp(Heap &heap, int index)
  { 
  	if(index<0 || index >= heap.size)
  		{//Is greater than the maximum value of the heap
  			 return return; 
  		}
  	while(index>0)
  	  { 
  		int temp = heap.arr[index];
  		int parent = (index - 1) / 2; 
  		if(parent >= 0)
  		  {   //If the index is not out of bounds, perform the desired operation
  			if(temp > heap.arr[parent])
  			{ 
  			  heap.arr[index] = heap.arr[parent]; 
  			  heap.arr[parent] = temp; index = parent; 
  			}else {
  			//If you are younger than your father, end the cycle directly
  			 break; 
  			 } 
  			}
  		else {
  		//Out of bounds end cycle 
  		break;
  		 } 
  	  } 
  }


/*Insert nodes at the end of the maximum heap while ensuring the characteristics of the maximum heap*/
 bool insert(Heap &heap, int value)
  {
   if (heap.size == heap.capacity)
    { fprintf(stderr, "Stack space exhausted!\n");
      return false;
    }
   int index = heap.size;
   heap.arr[heap.size++] = value;
   adjustUp(heap, index);
   return true; 
   }

Heap top element dequeue
When inserting nodes, we insert new values at the end of the array. Now let's do the opposite: we take the last element in the array, put it at the top of the heap, and then fix the heap properties.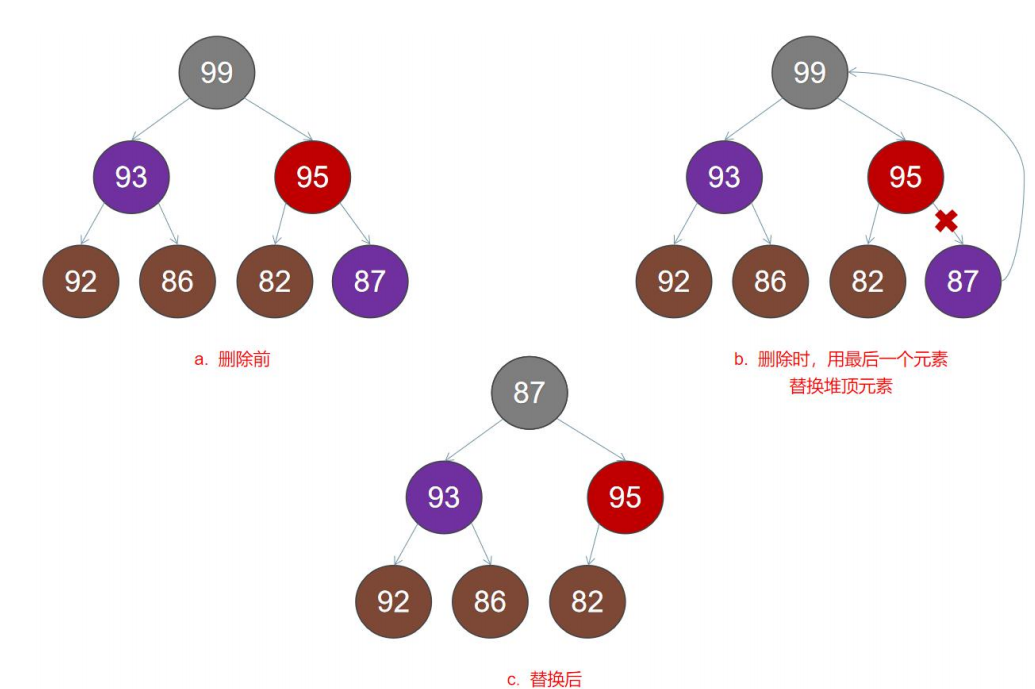

/*Adjust the current node and child nodes to the maximum heap*/ 
void adjustDown(Heap &heap, int index)
 { 
   int cur = heap.arr[index];//Current node to be adjusted
   int parent, child; 
   /*Judge whether there is a sub node larger than the current node. If it does not exist, the heap itself is balanced and does not need to be adjusted;
   If it exists, exchange the largest child node with it. After the exchange, if this child node has children, continue
   Follow the same steps to adjust this child node */
   for (parent = index; (parent * 2 + 1)<heap.size; parent = child)
    { 
      child = parent * 2 + 1; //Take the largest of the two child nodes
      if (((child + 1)<heap.size) && (heap.arr[child]<heap.arr[child + 1]))
       { child++; }
       //Judge whether the largest node is larger than the current parent node 
      if (cur >= heap.arr[child]) 
        {//No more than, no adjustment is required and the loop is skipped
         break; 
        }else
        {//Greater than the current parent node, swap, and then continue to adjust downward from the child node position
         heap.arr[parent] = heap.arr[child];
         heap.arr[child] = cur; 
         } 
     } 
  }



//Delete the largest node and get the value of the node
bool popMax(Heap &heap,int &vaule)
 {
    if(heap.size<1)   return false;
    
    vaule=heap.arr[0];
    //Carry out the operation in Figure b, and put the last node into the root node
    heap.arr[0]=heap.arr[--heap.size];
    //Make it the largest heap from top to bottom
    addjustDown(heap,0);