Basic concepts of Huffman

 
Path: the branch from one node to another in the tree forms the path between the two nodes
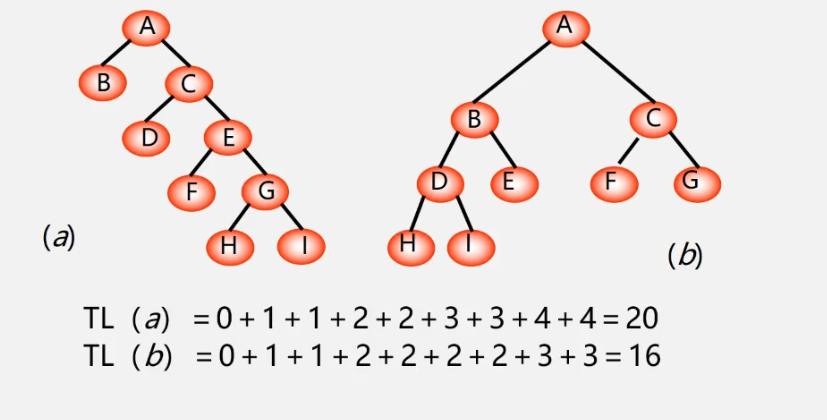
Node path length: the number of branches on the path between two nodes

 

Path length of tree: the sum of the path length from the tree root to each node is recorded as TL

In the binary tree with the same number of nodes, the complete binary tree is the shortest binary tree
 
 

Weight: assign a node in the tree to a value with a certain meaning, then this value is called the weight of the node

Weighted path length of a node: the product of the path length from the root node to the node and the weight of the node

Weighted path length of tree (WPL): the sum of weighted path lengths of all leaf nodes in the tree
Record as: W P L = ∑ i = 0 k w k l k WPL=\sum_{i=0}^{k} w_ k l_k WPL=i=0∑k​wk​lk​
ω \omega ω—— Weight    l k l_k lk -- path length from node to root

 
 

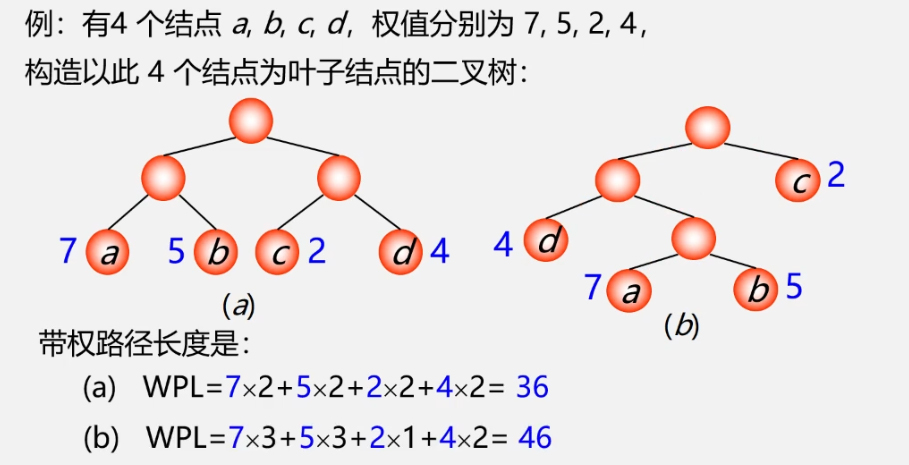
Huffman tree: optimal tree - the tree with the shortest weighted path length (WPL)

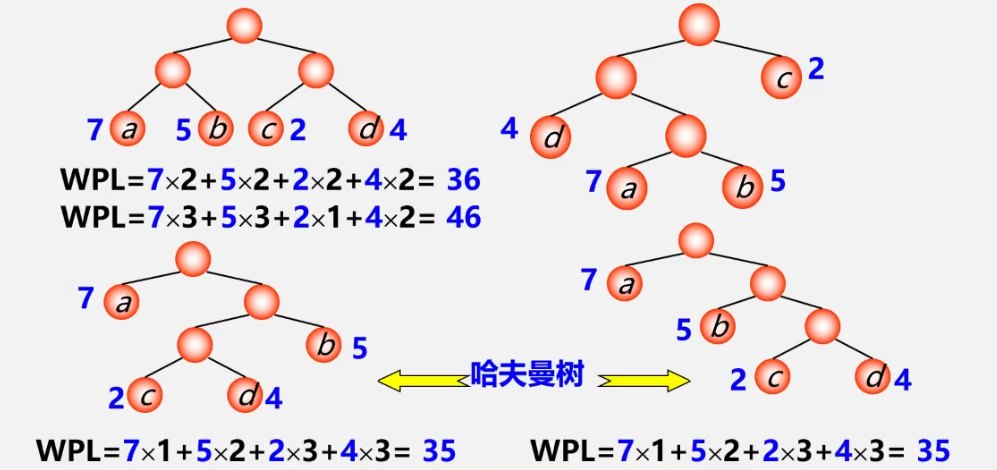
1. A full binary tree is not necessarily a Huffman tree
2. The more powerful the leaf in the Huffman tree, the closer it is to the root
3. Huffman trees with the same weighted nodes are not unique

 
 

Construction algorithm of Huffman tree

 

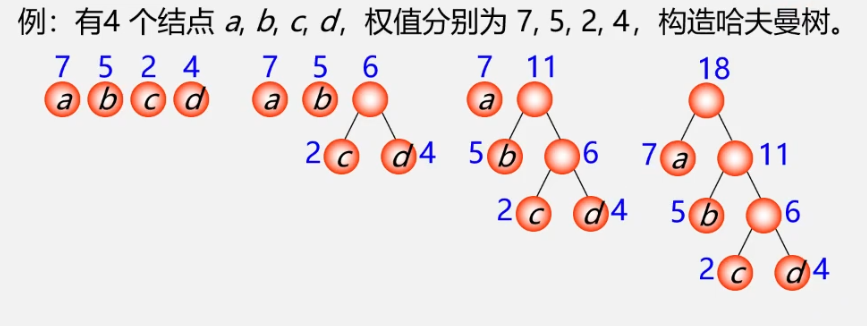
Greedy algorithm: to construct Huffman tree, first select the leaf node with small weight

Huffman algorithm (method of constructing Huffman tree)

Pithy formula:

1. Structural forests are all roots;
2. Select two small trees to build new trees;
3. Delete two new people
4. Repeat 2 and 3, leaving a single piece

 

The degree of the node of Huffman tree is 0 or 2, and there is no node with degree 1;

The Huffman tree with n leaf nodes has 2n-1 nodes;

The forest containing N trees must be merged n-1 times to form Huffman tree, with n-1 new nodes;
 

Summary:

1. In Huffman algorithm, there are N binary trees at the beginning, which need to be merged n-1 times to finally form Huffman tree
2. After n-1 merging, n-1 new nodes are generated, and these n-1 new nodes are branch nodes with two children

It can be seen that the Huffman tree has n+n-1 = 2n-1 nodes, and the degree of all its branch nodes is not 1
 
 

Implementation of Huffman tree construction algorithm

 
Using sequential storage structure -- one-dimensional structure array
Node type definition:

typedef struct{
	int weight;
	int parent, lch, rch;
}HTNode, *HuffmanTree;

The Huffman tree has 2n-1 nodes in total, does not use 0 subscript, and the array size is 2n
 

For example, if the weight of the first node is 5, it can be expressed as H [i] weight = 5;

 

Example: n = 8, weight W = {7, 19, 2, 6, 32, 3, 21, 10}, construct Huffman tree

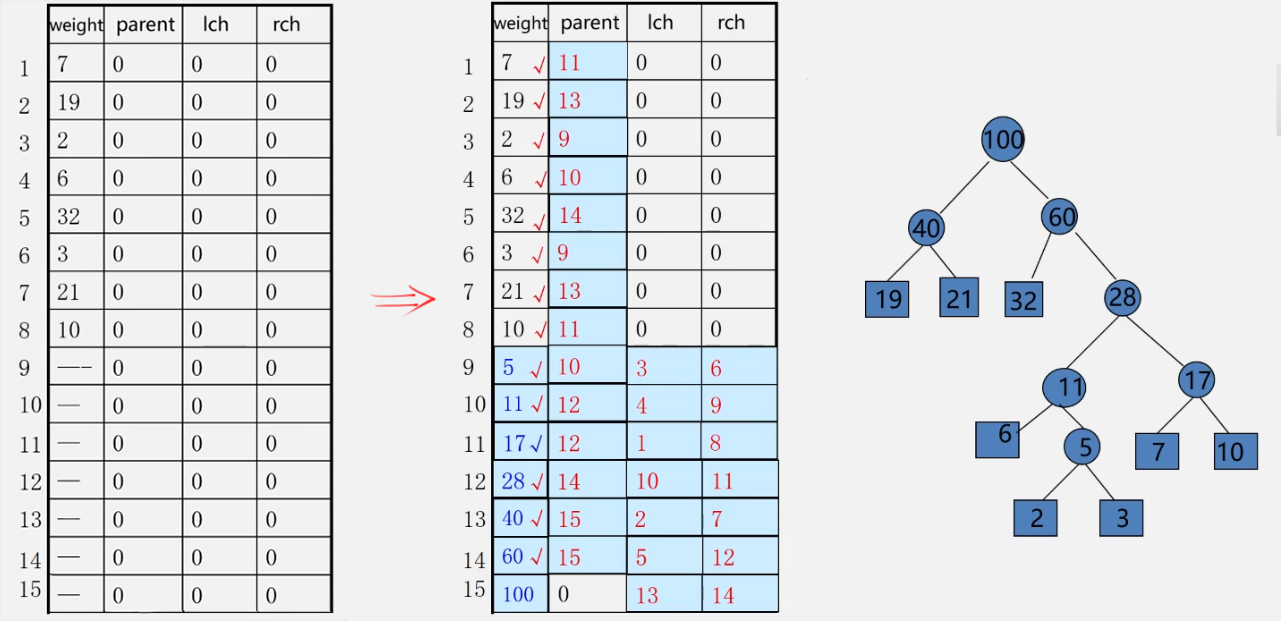
1. Initialize HT [1... 2n-1]: lch = rch = parent = 0;
2. Enter the initial n leaf nodes: set the weight value of HT[1... N]
3. Perform the following n-1 merges to generate n-1 nodes HT[i], i = n+1... 2n-1
   a)   in HT[1... i-1, select two nodes HT[s1] and HT[s2] with the smallest weight that have not been selected (from the nodes with parent==0), and s1 and s2 are the subscripts of the two smallest nodes;
   b)   modify the parent values of HT[s1] and HT [S2]:   HT[s1] parent=i;  HT[s2].parent = i;
   c)   modify the newly generated HT[i]:
     1) HT[i].weight = HT[s1].weigth + HT[s2].weight;
     2) HT[i].lch = s1; HT[i].rch = s2;

//Constructing Huffman tree -- Huffman algorithm
void CreatHuffmanTree(HuffmanTree &HT, int n){
	if(n <= 1) return;
	m = 2 * n - 1;		//The array has 2n-1 elements in total
	HT = new HTNode[m + 1];		//Unit 0 is not used, HT[m] represents the root node
	for(i =1; i <= m; ++i){		//Set lch, rch and parent of 2n-1 elements to 0
		HT[i].lch = 0;
		HT[i].rch = 0;
		HT[i].parent = 0;
	}
	for(i = 1; i <= n; ++i)
		cin >> HT[i].ewight;	//Enter the weight value of the first n elements
	//After initialization, let's start building Huffman tree

	//Merging to produce n-1 nodes -- Constructing Huffman tree
	for(i = n + 1; i <= m; i++){	
		Select(HT, i - 1, s1, s2);	//Select two in HT[k] (1 ≤ K ≤ i-1) whose parental domain is 0,
									//And the node with the smallest weight, and return their sequence numbers s1 and s2 in HT
									
		HT[s1].parent = i;		//Indicates that s1 and s2 are deleted from F
		HT[s2].parent = i;
		
		HT[i].lch = s1;			//s1 and s2 are the left and right children of i respectively
		HT[i].rch = s2;

		HT[i].weight = HT[s1].weight +HT[s2].weight;	//The weight of i is the sum of the weight of left and right children
	}
}

 

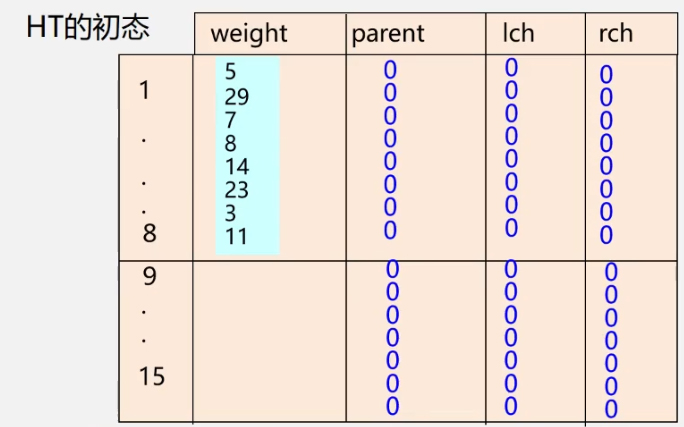
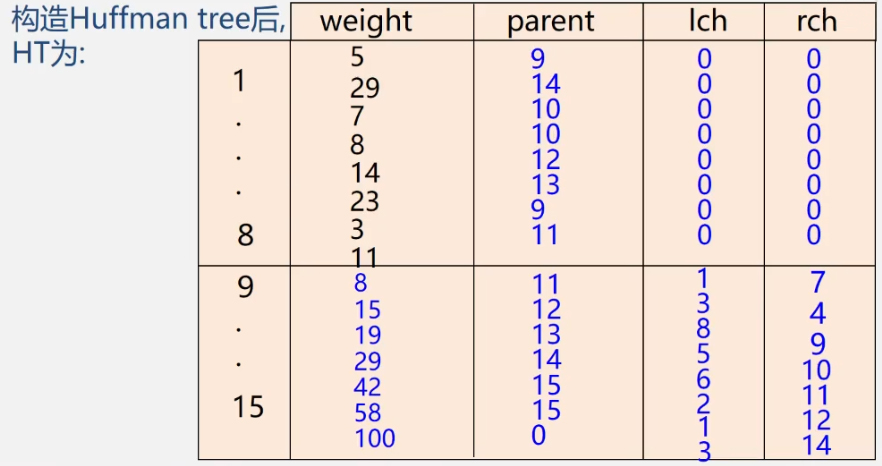
Example: let n = 8, w = {5, 29, 7, 8, 14, 23, 3, 11}, and try to design Huffman code

(m = 2*8-1 = 15)


 
 

Huffman coding

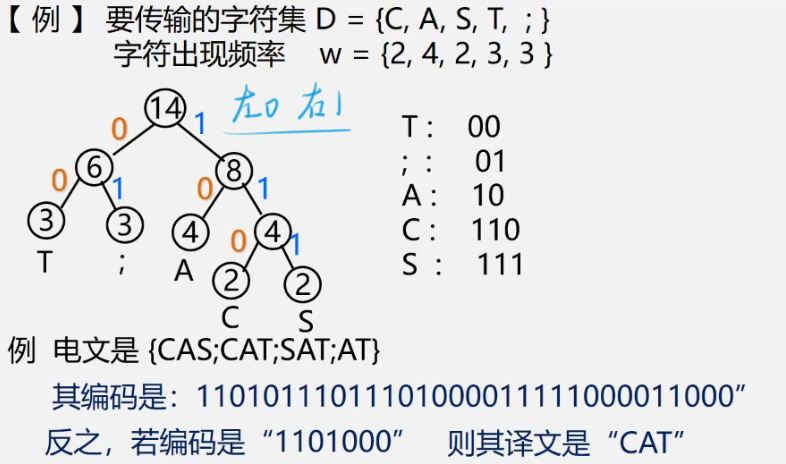
Question: what prefix code can make the total length of the message shortest—— Huffman coding

1. Count the average probability of each character in the character set appearing in the message (the greater the probability, the shorter the code is required)
2. Using the characteristics of Huffman tree: the greater the weight, the closer the leaf is to the root; Taking the probability value of each character as the weight to construct Huffman tree, the node with higher probability will have shorter path
3. Mark 0 or 1 on each branch of Huffman tree:
      node left branch mark 0, right branch mark 1
     connect the labels on the path from the root to each leaf as the encoding of the characters represented by the leaf

 

Explanation of Huffman coding algorithm: https://www.bilibili.com/video/BV1nJ411V7bdp=106&spm_id_from=pageDriver

Implementation of Huffman coding algorithm:

//The Huffman code of each character is obtained from the leaf to the inverse root and stored in the coding table HC
void CreatHuffmanCode(HuffmanTree HT, HuffmanCode &HC, int n){
	HC = new char *[n + 1];			//Allocate n character encoded header pointer vectors
	cd = new char [n];				//Allocate dynamic array space for temporarily storing codes
	cd[n - 1] = '\0' ;				//Code Terminator
	for(i = 1; i <= n; ++i){		//Huffman coding character by character
		start = n - 1;
		c = i;
		f = HT[i].parent;
		while(f != 0){			//Trace back from the leaf node to the root node
			--start;			//Backtracking once start points forward to a position
			if(HT[f].lchild == c)		//If node c is the left child of f, the production code is 0
				cd[start] = '0' ;		
			else						//If node c is the right child of f, code 1 is generated
				cd[start] = '1' ;
			c = f;				//Keep going back up
			f = HT[f].parent;
		}						//Find the coding of the ith character	
		HC[i] = new char [n - start];		//Allocate space for the ith string encoding
		strcpy(HC[i], &cd[start]);			//Copy the obtained code from the temporary space cd to the current line of HC
	}
	delete cd;		//Free up temporary space
} //CreatHuffanCode

 
 

Encoding and decoding of documents

1, Code:

  ① input each character and its weight

  ② construct Huffman tree - HT[i]

  ③ Huffman coding - HC[i]

  ④ check HC[i] to get Huffman code of each character

2, Decoding:

  ① construct Huffman tree

  ② read in binary codes in sequence

  ③ read 0 and go to the left child; Read 1 and go to the right child

  ④ once a leaf is reached, characters can be translated

⑤ then continue decoding from the root until the end

Explanation: https://www.bilibili.com/video/BV1nJ411V7bd?p=107