Huffman tree

definition:

Given N weights as N leaf nodes, a binary tree is constructed. If the weighted path length of the tree reaches the minimum, such a binary tree is called the optimal binary tree, also known as Huffman tree. Huffman tree is the tree with the shortest weighted path length, and the node with larger weight is closer to the root.

understand:

Take chestnuts for example: if you have a wardrobe with ABCDEF, there are 6 clothes in total, but the frequency of wearing each clothes is different, 54% (ask is like wearing), 10%, 6%, 3%, 7%, 20%
So now the question is, how can you put your clothes in order to avoid making a mess of the wardrobe every time you look for clothes?
The answer must be to put the one with high frequency in your nearest place
you 're right!! Huffman tree is like this

Let's see how to build a Huffman tree to complete this operation

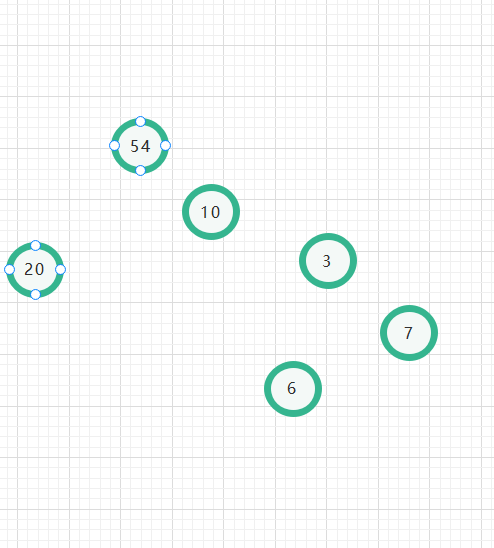
Just remember one sentence: find the two smallest vertices to merge

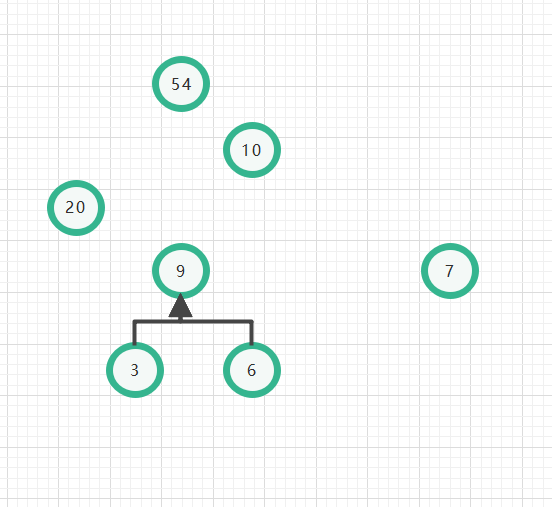
Then keep repeating, keep repeating~~

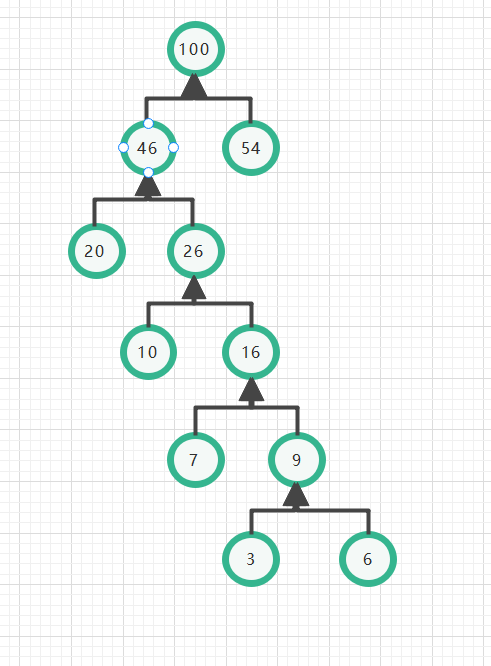
Obviously~~~
You can find
Each of its leaves is clothes, and the root of the tree with the highest frequency is the nearest
This forms a Huffman tree


Here's the point

Huffman coding

We know that there are many coding methods, such as ASCII coding, binary coding and so on
A Huffman code is introduced below
Or the clothes on it
We stipulate that the right subtree is 1 and the left subtree is 0 (that is, looking right is 1 and looking left is 0)
You can analyze it according to the figure

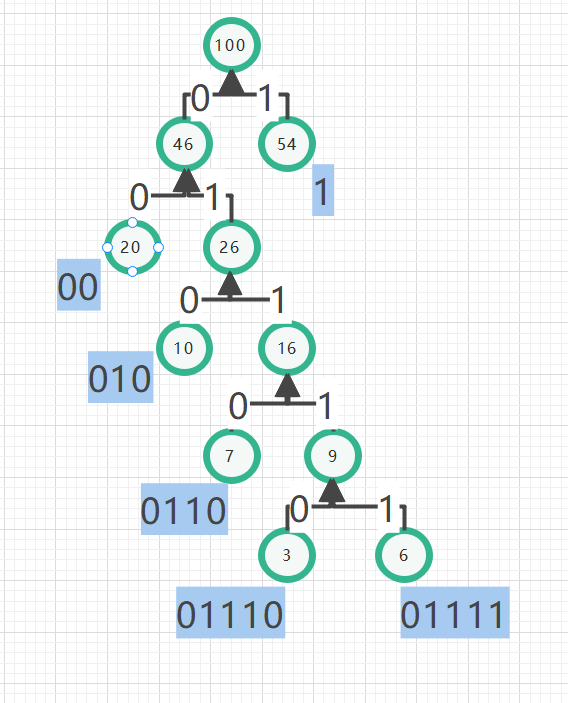
For the above clothes, we can use ASCII coding or binary coding
Of course, Huffman coding can also be used
Let's analyze which is the most efficient (that is, coding with the shortest code length)
A S C I I : 8 b i t ASCII: 8bit ASCII: 8bit
two enter system : 3 b i t Binary: 3bit Binary: 3bit
Huffman coding: because of the indefinite length of Huffman coding, we require the average code length ACL
A C L = 0.54 ∗ 1 + 0.20 ∗ 2 + 0.10 ∗ 3 + 0.07 ∗ 4 + 0.09 ∗ 5 = 1.97 ACL=0.54*1+0.20*2+0.10*3+0.07*4+0.09*5 = 1.97 ACL=0.54∗1+0.20∗2+0.10∗3+0.07∗4+0.09∗5=1.97

obviously!! Huffman is smaller than the other two coding lengths

Next, we use code to realize the construction of Huffman tree

Better understanding combined with tables~~~
This form has also become a codec table. It can be said that if you use Huffman coding to send messages to your friends, the internet police will never find it no matter how powerful it is

node	character	probability	parent node	left node	right node	code
1	A	54	11	0	0	1
2	B	10	9	0	0	010
3	C	6	7	0	0	01111
4	D	3	7	0	0	01110
5	E	7	8	0	0	0110
6	F	20	10	0	0	00
7		9	8	4	3
8		16	9	5	7
9		26	10	2	8
10		46	11	6	9
11		100		10	1

Huffman tree node structure

struct HTNode
{
	char ch;   //Corresponding letters, such as a
	int weight;//The number of occurrences of letters, such as 1000 occurrences of a
	int parent;
	int left;
	int right;
	char* code;
};

Initialize tree structure

void InitHTTable(int AsciiCount[], HTNode* &HT)
{
	for(int i = 0; i <= 128; i ++) AsciiCount[i] = 0;//Initialize array to 0
	
	AsciiCount[65] = 54;
	AsciiCount[66] = 10;
	AsciiCount[67] = 6;
	AsciiCount[68] = 3;
	AsciiCount[69] = 7;
	AsciiCount[70] = 20;
	
	HT=new HTNode[2 * 6];//Generate dynamic space [1...2n-1]
	int	CurrentASCII=0;//Current ASCII code
	HT[0].weight=0;
	for(int i = 1; i <= 6; i ++)
	{
		while(AsciiCount[CurrentASCII] == 0)//There may be a break in ASCII. Find the character whose count is not zero
			CurrentASCII++;
			
		HT[i].ch = CurrentASCII;//j is the ASCII code of the character whose count is not zero
		HT[i].weight = AsciiCount[CurrentASCII];//This is the number of occurrences of the character j as Huffman's weight
		HT[i].parent = 0;//Initialize parents
		HT[i].left = 0;//Initialize left child
		HT[i].right = 0;//Initialize right child
		
		CurrentASCII++;//Next ASCII code
	}
}

Find the two smallest probabilities

void selectMin(HTNode* &HT,int end,int &min1,int &min2)
{//In the array HT[1...end], find the two with the smallest weight
	int i;
	min1 = 0;
	min2 = 0;
	for(i = 1; i <= end; i++)
	{
		if(HT[i].parent != 0)//If this node already has parents, it means that it is already in the tree
			continue;
		else
		{
			if(min1 == 0)
				min1 = i;//Note the minimum value
			else if(HT[i].weight < HT[min1].weight)//Smaller value found
				min1 = i;			
		}
	}

	for(i = 1; i <= end; i++)
	{ 
		if(HT[i].parent != 0 || i == min1)
			continue;
		else
		{
			if(min2 == 0)
				min2 = i;
			else if(HT[i].weight < HT[min2].weight)
				min2 = i;			
		}
	}

	if(min1 > min2)
	{//Make sure min1 is minimum
		int t = min1;
		min1 = min2;
		min2 = t;
	}

}

Build a tree

void createHT(HTNode* &HT)
{//Create Huffman tree and get Huffman code
	int i = 0;
	for(i = 0; i <= 11; i++)
	{//Initialize all Huffman tables
		HT[i].parent=0;
		HT[i].left=0;
		HT[i].right=0;
	}

	for(i = 7; i <= 11; i++)
	{//Form Huffman tree
		int min1, min2;
		selectMin(HT, i - 1, min1, min2);//Select two minimum values from the i-1 items in front of the Huffman table, min1 is the minimum, and the left subtree of the constructed Huffman tree is small
		HT[min1].parent = i;
		HT[min2].parent = i;
		HT[i].weight = HT[min1].weight + HT[min2].weight;//Two small probabilities synthesize a node
		HT[i].left = min1;
		HT[i].right = min2;
	}

	//Huffman node generating leaves
	int code_length = 0;

	for(i = 1; i <= 6; i++)
	{
		char code[128];//Save Huffman code
		int j = i, k = 0;
		while(1)
		{
			int parentPosition = HT[j].parent;
			if(parentPosition == 0)
			{//This is the root node
				code[k] = '\0';
				HT[i].code = new char[k + 1];
				for(int x = 0; x < k; x++)
					HT[i].code[x] = code[k - 1 - x];
				HT[i].code[k] = '\0';
				
				printf("%c : %d : %s\n",HT[i].ch, HT[i].weight, HT[i].code);// Output character probability and coding value 
				break;
			}

			if(HT[parentPosition].left == j)
				code[k++] = '0';
			else
				code[k++] = '1';

			j = parentPosition;
		}
	}
}

Sprinkle flowers at the end 🌼🌻🌼🌻