Before we started learning and collecting, we also looked for some information in advance.
Recommend this blogger's article; Explain and collect easy to understand. Know the blogger: Pecco --> Algorithmic Learning Notes (1): and collect
Can be used and collected to solve node connection problems on the network; Specifically speaking right two functions; (1) Determine if two points are connected, (2) Connect if they are not connected
First, define a generic interface UnionSet before implementation.
When using and collecting, you don't care about element content.
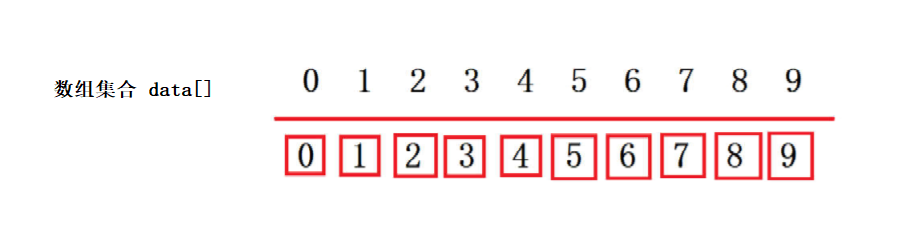
So you can save elements using arrays, where p and q correspond to the index of the array in which they are located
/**
* @author by CSDN@Smart RE0
* @date 2021-12-08
* Find Common Interfaces
*/
public interface UnionSet {
/**
* Connection method defined
* @param p The current index of the elements of the first collection
* @param q The element current index of the second set
*/
void toUnion(int p, int q);
/**
* Determine whether two sets are connected
* @param p Current index of elements in set 1
* @param q Current index of elements in set 2
* @return Connect or not
*/
boolean isConnection(int p, int q);
/**
* Returns the number of elements in the current collection;
* @return Number of elements
*/
int getSize();
}
📢 Implementation 1: Using array base implementation
process
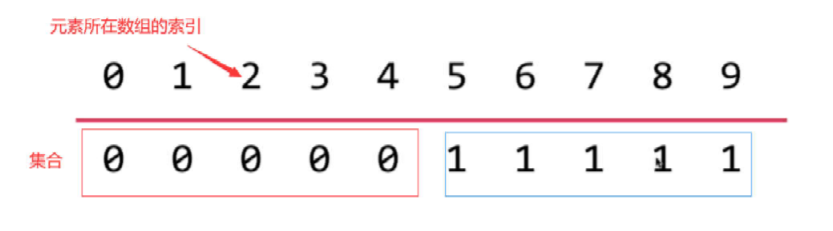
For example, you can think of each element in an array as a separate set;
For example, to see if Nodes 1 and 4 are connected; The content of the array element found in Node 1 is 1, and that of Node 4 is 0. Not equal, so no connection;
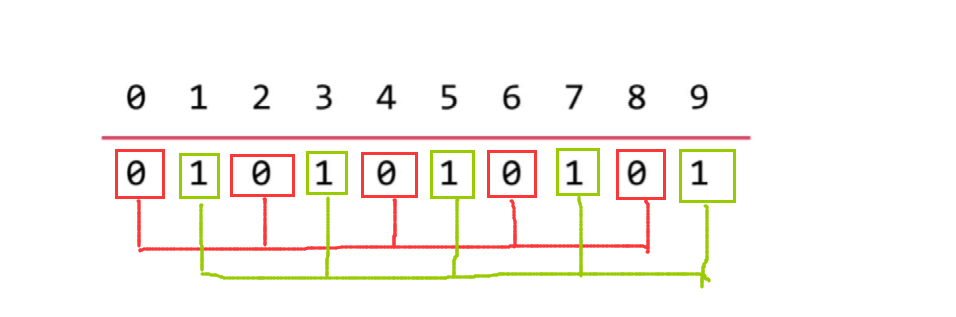
To connect Node 1 and Node 4, you actually have to combine the sets they belong to.
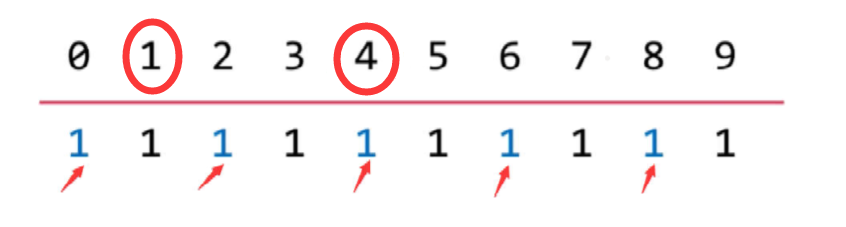
Replace all collection elements of the collection to which node 4 belongs with 1;
code implementation
import com.company.unionset.UnionSet;
/**
* @author by CSDN@Smart RE0
* @date 2021-12-08
* Mode 1:: Array base implementation and collection;
*/
public class RealUnionSet01 implements UnionSet {
//An array of stored elements;
int[] data;
//Initialization;
public RealUnionSet01(int len){
this.data = new int[len];
//Save elements into the array;
for (int i = 0; i < len; i++) {
this.data[i] = i;
}
}
//The corresponding element used to find the current index;
public int findEle(int index){
return this.data[index];
}
@Override
public void toUnion(int p, int q) {
//Find the corresponding elements of the two indexes;
int pEle = findEle(p);
int qEle = findEle(q);
if(pEle!=qEle) {
//The elements of the first set are uniformly reset to those of the second set;
for (int i = 0; i < this.data.length; i++) {
if (findEle(i) == pEle) {
this.data[i] = qEle;
}
}
}
}
@Override
public boolean isConnection(int p, int q) {
//Find the corresponding elements of the two indexes separately;
int pEle = findEle(p);
int qEle = findEle(q);
return pEle == qEle;
}
@Override
public int getSize() {
return data.length;
}
}
Test 1
/**
* @author by CSDN@Smart RE0
* @date 2021-12-08
* Implemented by Test Mode 1
*/
public class Test01 {
public static void main(String[] args) {
int len = 100000;
int num = 100000;
RealUnionSet01 rs1 = new RealUnionSet01(len);
test1(rs1,num);
}
/**
* Testing num connections under union set
* @param rs And Search Sets
* @param num frequency
*/
public static void test1(UnionSet rs, int num){
long startTime = System.nanoTime();
//Use random number classes;
Random rd = new Random();
for (int i = 0; i < num; i++) {
int n1 = rd.nextInt(rs.getSize());
int n2 = rd.nextInt(rs.getSize());
rs.toUnion(n1,n2);
}
long endTime = System.nanoTime();
System.out.println("Connection time"+(endTime-startTime)/1000000000.0);
}
}
Connection time 6.4901904
📢 Implementation 2: Array-based, tree-structured implementation
process
At first each node is self-connected;
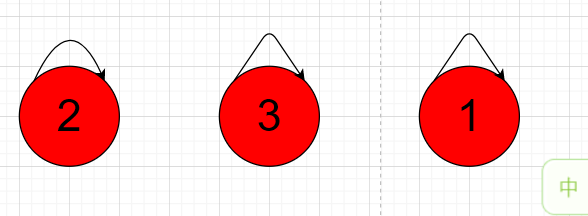
To connect Node 2 and Node 3, Node 1 is still self-connected
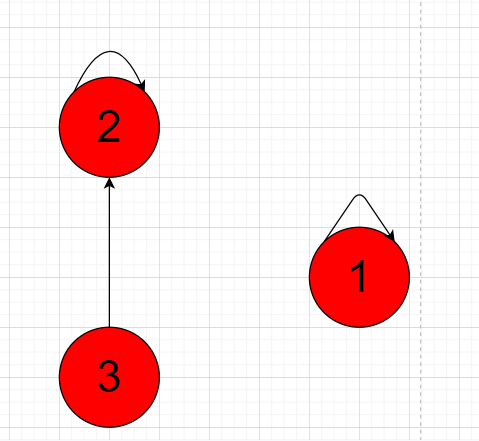
Then connect Node 1 to Node 3, as long as the root nodes of Node 1 and Node 3 are connected.
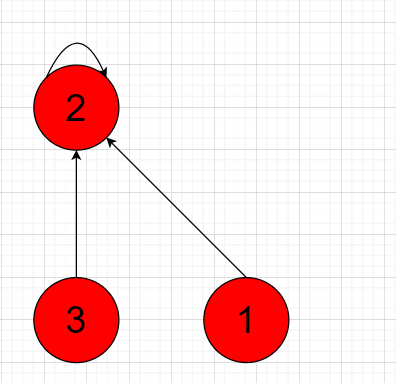
As long as the top node of the tree where the node is located is the same, the two trees are considered connected.
Top node features: >>> Its parent node is itself,
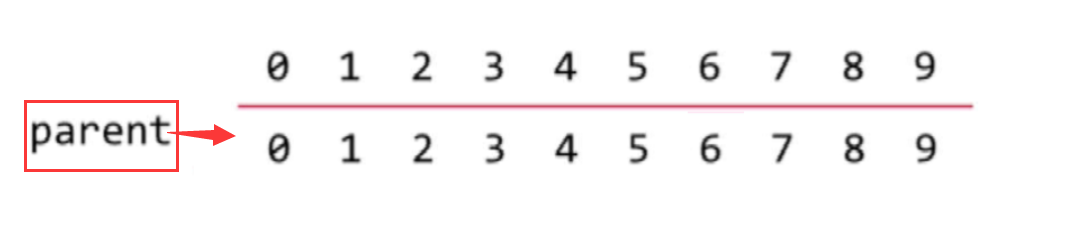
For example, using arrays as the underlying structure initially points to itself; The top node of each node is itself; Make a self-connection;
In terms of tree structure, this is the following;

For example, node 3 and node 4 are connected; Node 3 is the top node of Node 4.
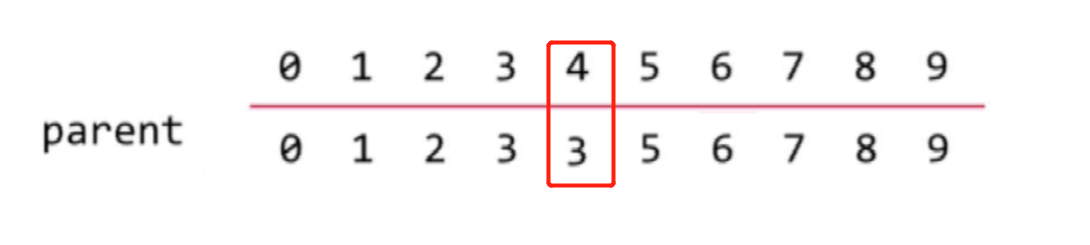

Then, to see if a node is connected, check if the elements indexed by that node are equal.
Connect Node 3 and Node 8; Change the parent node of node 3 to node 8
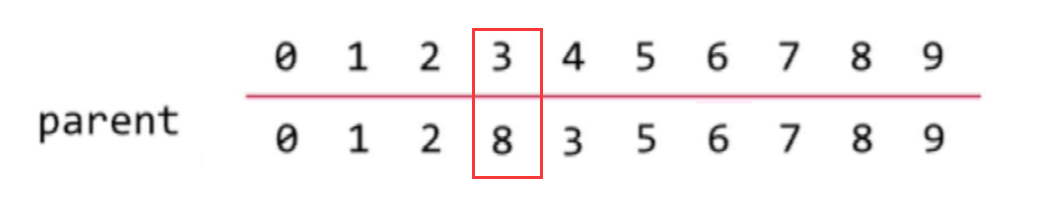

Connect Node 6 to Node 5; The parent node of node 6 can be changed to node 5.

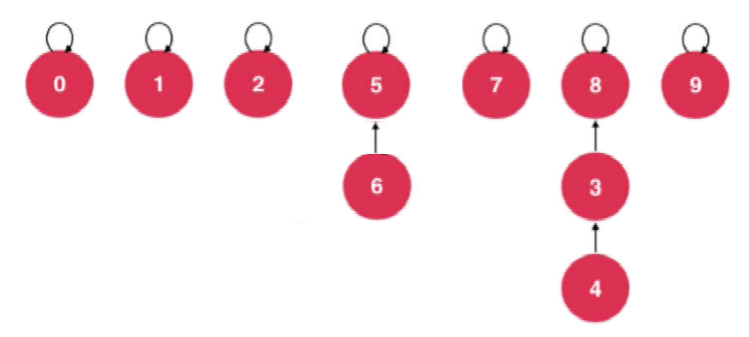
Connect Node 9 and Node 4; Node 9 points to the top node of Node 4.

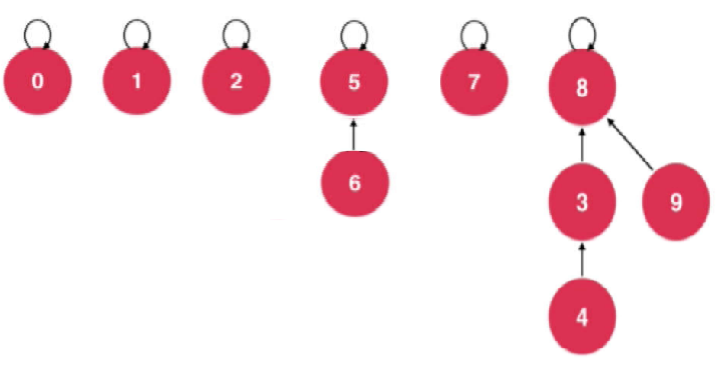
Connect Node 2 to Node 1,

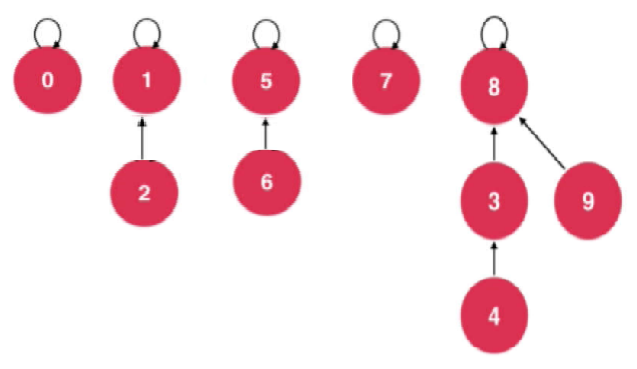
Connect node 5 to node 0;

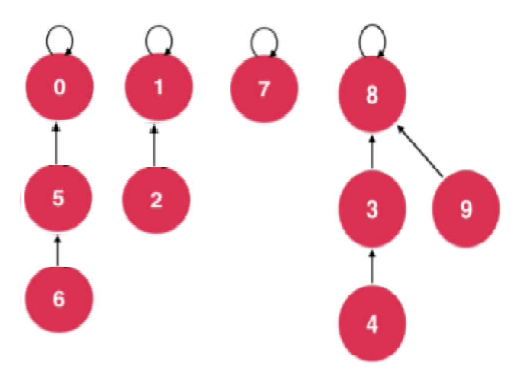
Connect nodes 7 and 2; Node 7 is connected to Node 2's parent Node 1;

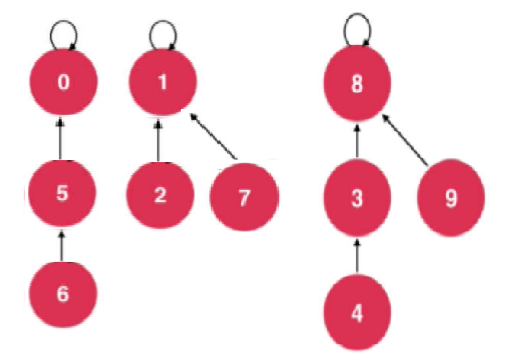
Node 6 and Node 2 are connected; Tie top node 0 of node 6 onto top node 1 of node 2

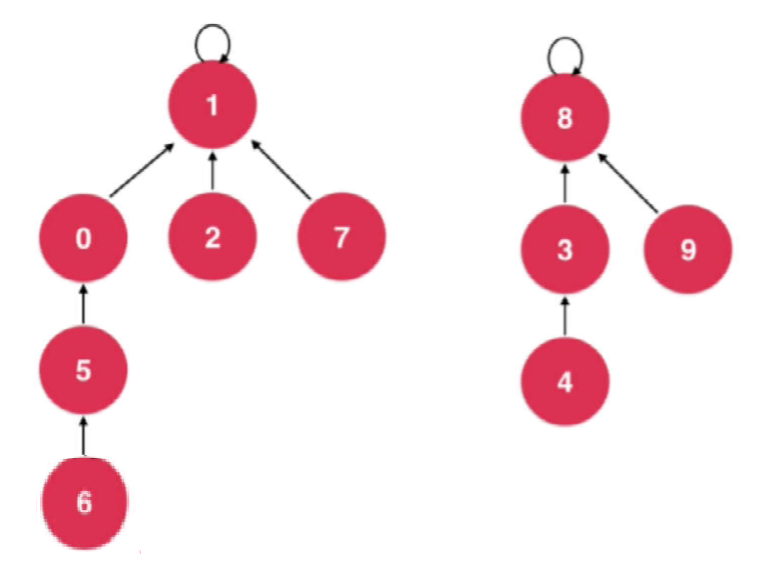
code implementation
import com.company.unionset.UnionSet;
/**
* @author by CSDN@Smart RE0
* @date 2021-12-08
* Mode 2:
*/
public class RealUnionSet02 implements UnionSet {
//Use arrays as the underlying structure; Is the element stored in the parent node;
int[] parent;
//Initialization;
public RealUnionSet02(int len){
this.parent = new int[len];
//Initialization is self-connected;
for (int i = 0; i < len; i++) {
this.parent[i] = i;
}
}
//Auxiliary methods; findParent;
private int findParent(int index){
while(index !=this.parent[index]){
index = this.parent[index];
}
return index;
}
@Override
public void toUnion(int p, int q) {
//Find the corresponding top-level elements of the two indexes respectively;
int pEle = findParent(p);
int qEle = findParent(q);
//If there is no connection, place the elements under the two indexes in the same place;
if(pEle!=qEle){
this.parent[pEle] = qEle;
}
}
@Override
public boolean isConnection(int p, int q) {
//Find the corresponding top-level elements of the two indexes respectively;
int pEle = findParent(p);
int qEle = findParent(q);
return pEle == qEle;
}
@Override
public int getSize() {
return this.parent.length;
}
}
Test 2
public class Test02 {
public static void main(String[] args) {
int len = 100000;
int num = 100000;
RealUnionSet02 rs2 = new RealUnionSet02(len);
test2(rs2,num);
}
/**
* Testing num connections under union set
* @param rs And Search Sets
* @param num frequency
*/
public static void test2(UnionSet rs, int num){
long startTime = System.nanoTime();
//Use random number classes;
Random rd = new Random();
for (int i = 0; i < num; i++) {
int n1 = rd.nextInt(rs.getSize());
int n2 = rd.nextInt(rs.getSize());
rs.toUnion(n1,n2);
}
long endTime = System.nanoTime();
System.out.println("Connection time"+(endTime-startTime)/1000000000.0);
}
}
Connection time 3.321709
📢 Implementation 3: (Optimized 2), adding an auxiliary array to store the number of nodes per tree
Use tree-structured
The complexity of the set is O(h), and in extreme cases, the tree will be deeper.
For example, when joining nodes 0 and 3, such a direct hook increases the depth of the tree; Reduce efficiency;
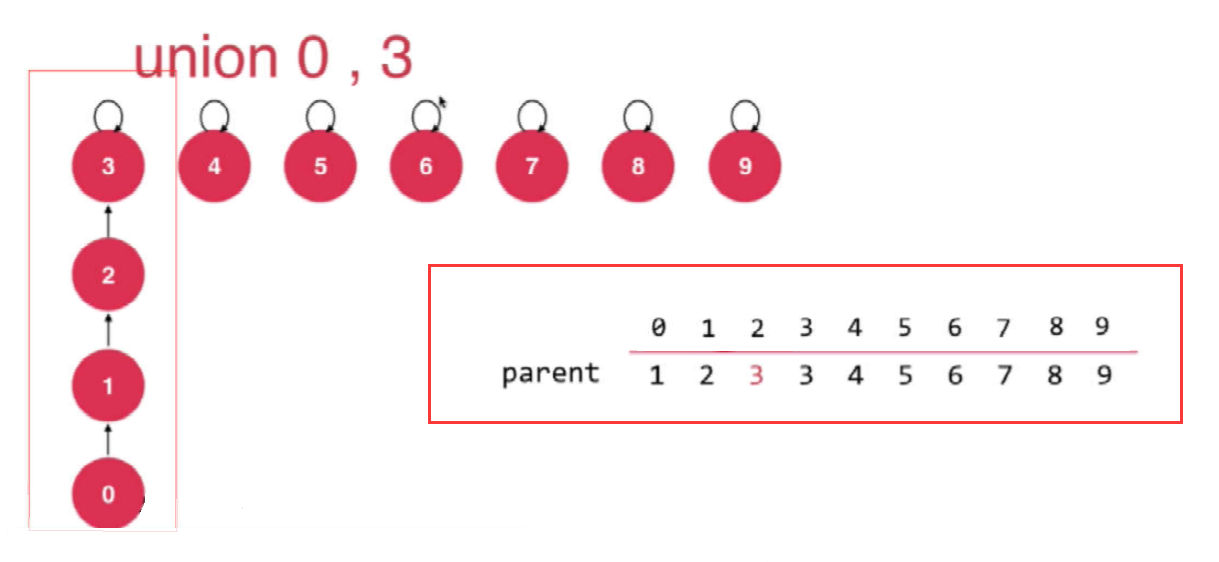
Optimize the connection operation of the tree; Connect the small tree to the big tree;
Merge trees with fewer elements into trees with more elements. Space needs to be created to store the number of elements per tree.
Then you need to create an array separately to store the number of nodes in the tree.
import com.company.unionset.UnionSet;
/**
* @author by CSDN@Smart RE0
* @date 2021-12-09
* Mode 3: (Optimize for implementation mode 2)
*/
public class RealUnionSet03 implements UnionSet {
//Use arrays as the underlying structure; Is the element stored in the parent node;
int[] parent;
//Store the number of nodes per tree;
int[] size;
//Initialization;
public RealUnionSet03(int len){
this.parent = new int[len];
this.size = new int[len];
//Initialization is self-connected;
for (int i = 0; i < len; i++) {
this.parent[i] = i;
//Initialize, each tree is connected independently;
this.size[i] = 1;
}
}
//Auxiliary methods; findParent;
private int findParent(int index){
while(index !=this.parent[index]){
index = this.parent[index];
}
return index;
}
//Optimize points; -->
@Override
public void toUnion(int p, int q) {
//Find the corresponding top-level elements of the two indexes respectively;
int pEle = findParent(p);
int qEle = findParent(q);
//If there is no connection, place the elements under the two indexes in the same place;
if(pEle!=qEle){
//Need to compare the number of nodes in the tree; Connect the small tree to the big tree;
if(size[pEle] >size[qEle]){
parent[qEle] = pEle;
size[pEle] += size[qEle];
}else{
parent[pEle] = qEle;
size[qEle] += size[pEle];
}
}
}
@Override
public boolean isConnection(int p, int q) {
//Find the corresponding top-level elements of the two indexes respectively;
int pEle = findParent(p);
int qEle = findParent(q);
return pEle == qEle;
}
@Override
public int getSize() {
return this.parent.length;
}
}
📢 Implementation 4: (Optimized 3) Merge by rank
Mode three does the operation of connecting a small tree to a large tree, but there is still a problem, which may happen to the tree in the following situation;
For example, after a series of connections,
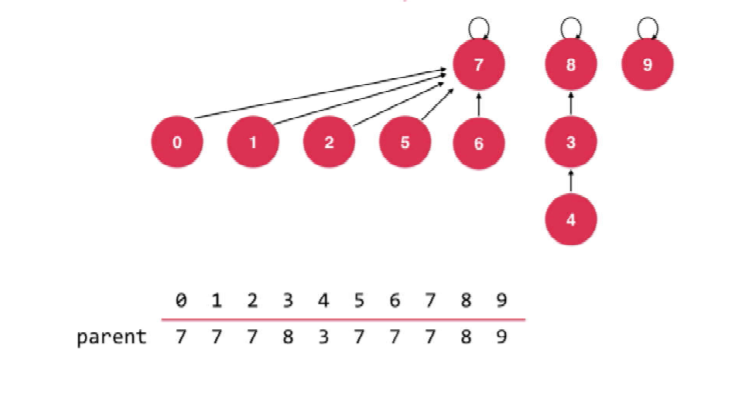
Node 4 and Node 2 will now be connected; Since node 2 is located in more tree nodes, it is necessary to merge the tree where node 4 is located into the tree where node 2 is located. That's what happened; It also affects efficiency;
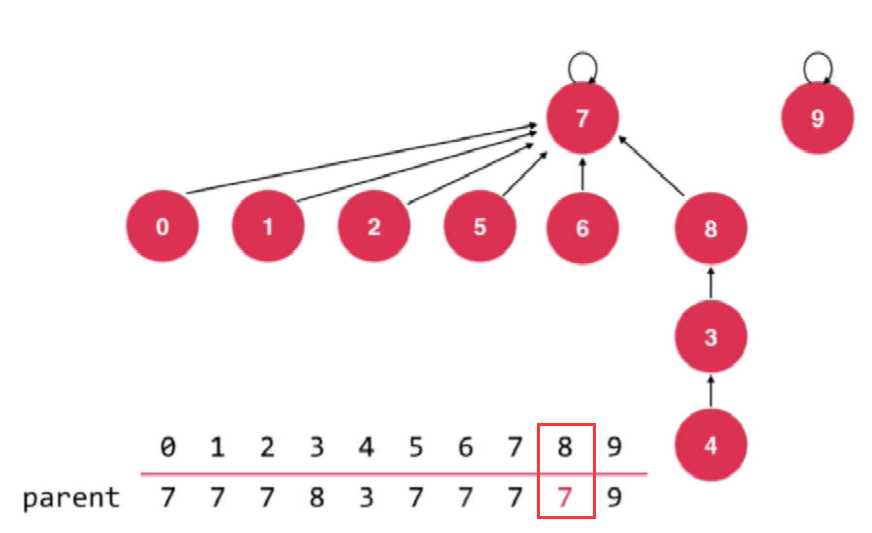
import com.company.unionset.UnionSet;
/**
* @author by CSDN@Smart RE0
* @date 2021-12-09
* Mode 4: (Optimize implementation mode 3) --> Optimize tree height;
* Merge by rank;
*/
public class RealUnionSet04 implements UnionSet {
//Use arrays as the underlying structure; Is the element stored in the parent node;
int[] parent;
//Store the height of each tree;
int[] rank;
//Initialization;
public RealUnionSet04(int len){
this.parent = new int[len];
this.rank = new int[len];
//Initialization is self-connected;
for (int i = 0; i < len; i++) {
this.parent[i] = i;
//Initialize, each tree is connected independently;
this.rank[i] = 1;
}
}
//Auxiliary methods; findParent;
private int findParent(int index){
while(index !=this.parent[index]){
index = this.parent[index];
}
return index;
}
//Optimize points; -->
@Override
public void toUnion(int p, int q) {
//Find the corresponding top-level elements of the two indexes respectively;
int pEle = findParent(p);
int qEle = findParent(q);
//If there is no connection, place the elements under the two indexes in the same place;
if (pEle != qEle) {
//Trees from low to high;
if (rank[pEle] > rank[qEle]) {
parent[qEle] = pEle; //Note that the height does not change;
} else if (rank[pEle] < rank[qEle]) {
parent[pEle] = qEle;
} else {
//If equal; After merging, the height will change;
parent[qEle] = pEle;
rank[pEle] += 1;
}
}
}
@Override
public boolean isConnection(int p, int q) {
//Find the corresponding top-level elements of the two indexes respectively;
int pEle = findParent(p);
int qEle = findParent(q);
return pEle == qEle;
}
@Override
public int getSize() {
return this.parent.length;
}
}
📢 Implementation 5: Path Compression
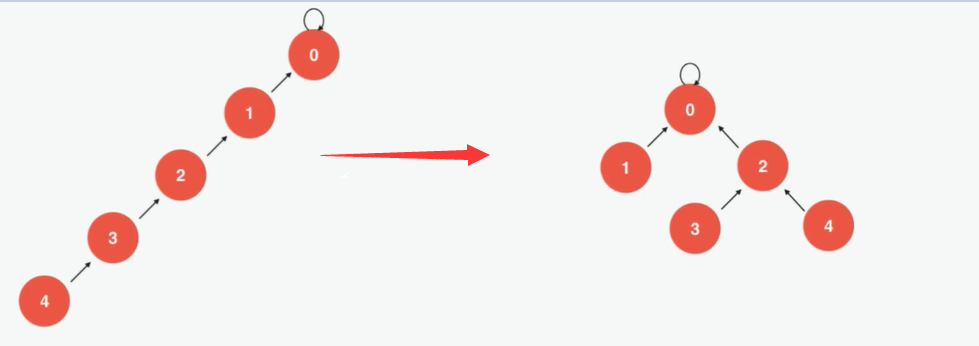
Specific process, can be seen as having node 4 as the current operation node and attaching it to parent node 2 of parent node 3;
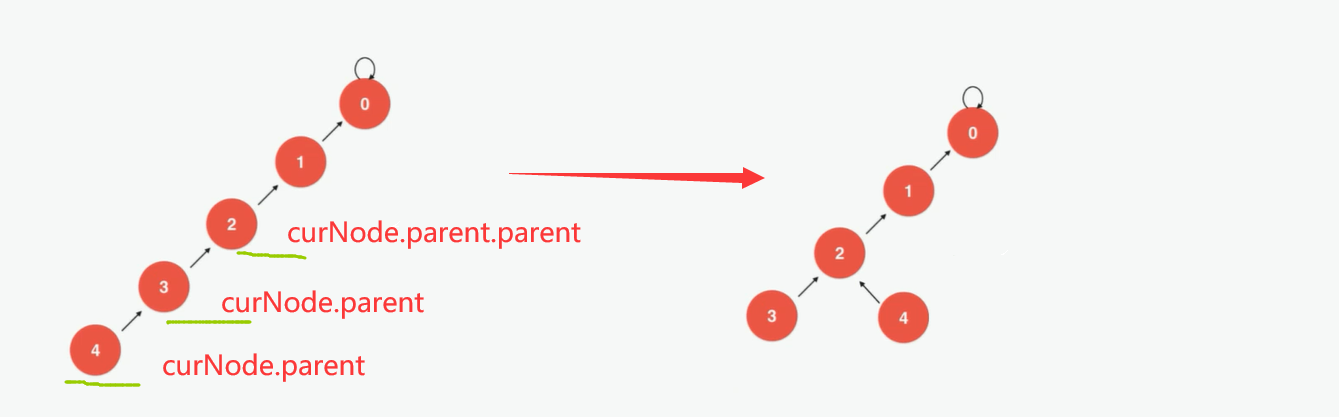
Then make Node 2 the current operation node; Let it be attached to parent node 0 of parent node 1;

import com.company.unionset.UnionSet;
/**
* @author by CSDN@Smart RE0
* @date 2021-12-09
* Mode 5: Path Compression
*/
public class RealUnionSet05 implements UnionSet {
//Use arrays as the underlying structure; Is the element stored in the parent node;
int[] parent;
//Store the height of each tree;
int[] rank;
//Initialization;
public RealUnionSet05(int len){
this.parent = new int[len];
this.rank = new int[len];
//Initialization is self-connected;
for (int i = 0; i < len; i++) {
this.parent[i] = i;
//Initialize, each tree is connected independently;
this.rank[i] = 1;
}
}
//Auxiliary methods; findParent; Optimize Points--->
private int findParent(int index){
while(index !=this.parent[index]){
//Join the parent node of the parent node of the current operation node to the current node;
parent[index] = parent[parent[index]];
//To update the operation node;
index = this.parent[index];
}
return index;
}
@Override
public void toUnion(int p, int q) {
//Find the corresponding top-level elements of the two indexes respectively;
int pEle = findParent(p);
int qEle = findParent(q);
//If there is no connection, place the elements under the two indexes in the same place;
if (pEle != qEle) {
//Trees from low to high;
if (rank[pEle] > rank[qEle]) {
parent[qEle] = pEle; //Note that the height does not change;
} else if (rank[pEle] < rank[qEle]) {
parent[pEle] = qEle;
} else {
//If equal; After merging, the height will change;
parent[qEle] = pEle;
rank[pEle] += 1;
}
}
}
@Override
public boolean isConnection(int p, int q) {
//Find the corresponding top-level elements of the two indexes respectively;
int pEle = findParent(p);
int qEle = findParent(q);
return pEle == qEle;
}
@Override
public int getSize() {
return this.parent.length;
}
}
📢 Implementation 6: Optimize
It can optimize and reduce the height of the tree.
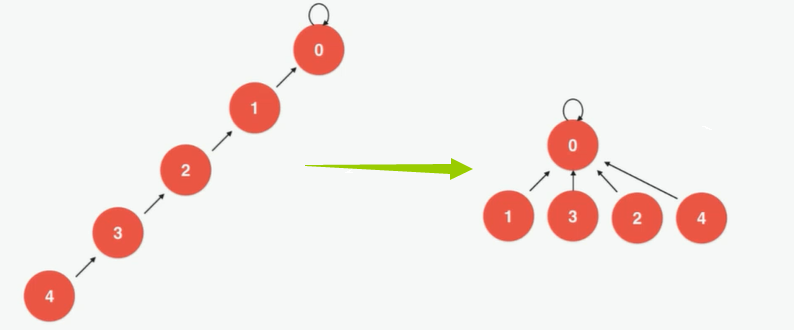
If this is implemented specifically, it needs to be optimized when looking up the node index. Layer by layer recursion,
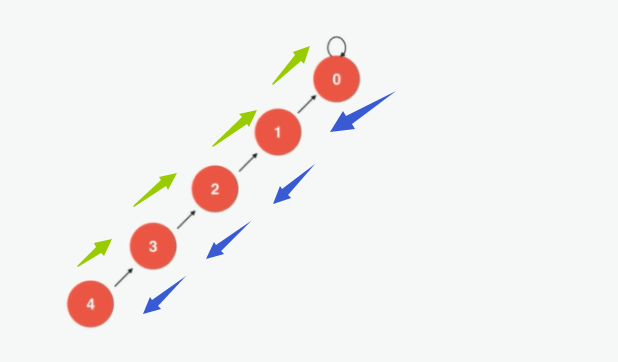
import com.company.unionset.UnionSet;
/**
* @author by CSDN@Smart RE0
* @date 2021-12-09
* Mode 6: Final optimization
*/
public class RealUnionSet06 implements UnionSet {
//Use arrays as the underlying structure; Is the element stored in the parent node;
int[] parent;
//Initialization;
public RealUnionSet06(int len){
this.parent = new int[len];
//Initialization is self-connected;
for (int i = 0; i < len; i++) {
this.parent[i] = i;
}
}
//Auxiliary methods; findParent; Optimize Points--->
private int findParent(int index){
if (index !=this.parent[index]){
//Recursively find parent node;
parent[index] = findParent(parent[index]);
}
return parent[index];
}
@Override
public void toUnion(int p, int q) {
//Find the corresponding top-level elements of the two indexes respectively;
int pEle = findParent(p);
int qEle = findParent(q);
//If there is no connection, place the elements under the two indexes in the same place;
if (pEle != qEle) {
parent[pEle] = qEle;
}
}
@Override
public boolean isConnection(int p, int q) {
//Find the corresponding top-level elements of the two indexes respectively;
int pEle = findParent(p);
int qEle = findParent(q);
return pEle == qEle;
}
@Override
public int getSize() {
return this.parent.length;
}
}