1. Concept

Binary search tree (also known as binary sort tree) can be an empty tree or a binary tree with the following properties:

• If its left subtree is not empty, the value of all nodes on the left subtree is less than the value of the root node
• If its right subtree is not empty, the values of all nodes on the right subtree are greater than those of the root node
• Its left subtree and right subtree are also binary search trees

By nature, we can easily draw a conclusion:

You can judge whether the binary tree is a search binary tree through medium order traversal. If the results are ordered, it is a search binary tree

Example diagram: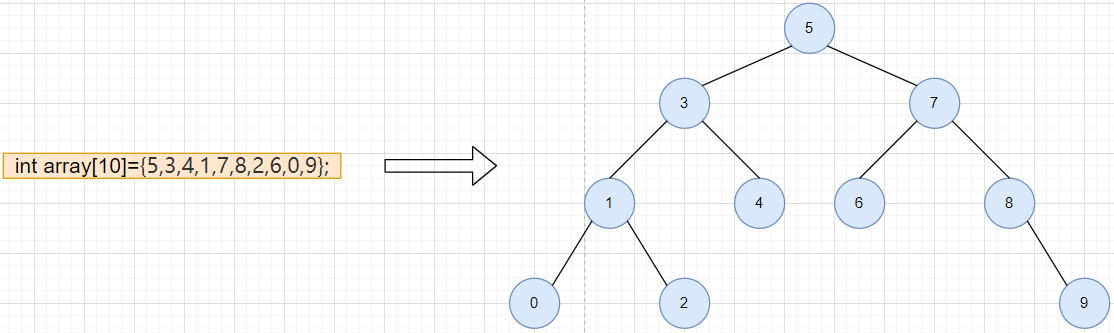

2. Operation

Before implementing the following operations on search binary tree, we will first write a basic search binary tree class to implement our operations in this class

Implementation code:

public class BinarySearchTree {
	// Define the node directly inside the binary tree class
    static class TreeNode{
        public int val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(int val){
            this.val=val;
        }
    }

    // lookup
    
    // insert
        
    // delete
}

2.1 search

Thought:

• If the node is not empty:
  • If the root node key = = lookup value key, return true
  • If the root node key > find value key, continue searching in its left subtree
  • If the root node key < search value key, continue to search in its right subtree
• Otherwise, false is returned

Implementation code:

// lookup
public TreeNode search(TreeNode root,int key){
    while(root!=null){
        if(root.val==key){
            return root;
        }else if(root.val>key){
            root=root.left;
        }else{
            root=root.right;
        }
    }
    return null;
}

2.2 insertion

Thought:

• If the following node is empty, it is inserted in the root node
• If it is not empty, find the leaf node where the value should be inserted to judge the insertion

Implementation code:

public void insertTree(int key){
    if (root==null){
        root=new TreeNode(key);
    }
    TreeNode cur=root;
    TreeNode parent=null;
    while(cur!=null){
        if(cur.val<key){
            parent=cur;
            cur=cur.right;
        }else{
            parent=cur;
            cur=cur.left;
        }
    }
    TreeNode node=new TreeNode(key);
    if(parent.val<key){
        parent.right=node;
    }else{
        parent.left=node;
    }
}

2.3 deletion

Thought:

• First find the node to be deleted by searching, and then set a node as its parent node
• After the deleted node is found
  • If the left node of the node to be deleted is empty
    • If the node to be deleted is the root node, let the root node be the right subtree
    • If the node to be deleted is not the root node and is the left subtree of the parent node, just make the left subtree of the parent node the right subtree of the node to be deleted
    • If the node to be deleted is not the root node and is the right subtree of the parent node, just make the right subtree of the parent node the right subtree of the node to be deleted
  • If the right node of the node to be deleted is empty
    • If the node to be deleted is the root node, let the root node be the left subtree
    • If the node to be deleted is not the root node and is the left subtree of the parent node, just make the left subtree of the parent node the left subtree of the node to be deleted
    • If the node to be deleted is not the root node and is the right subtree of the parent node, just make the right subtree of the parent node the left subtree of the node to be deleted
  • If the left and right nodes of the node to be deleted are not empty, use the replacement method to find the maximum value of the left subtree or the minimum value of the right subtree to replace the node to be deleted. In this way, we just need to delete the node to be replaced

Implementation code:

public void remove(int key){
    TreeNode cur=root;
    TreeNode parent=null;
    while(cur!=null){
        if(cur.val<key){
            parent=cur;
            cur=cur.right;
        }else if(cur.val==key){
            removeNode(cur,parent);
        }else{
            parent=cur;
            cur=cur.left;
        }
    }
}
public void removeNode(TreeNode cur,TreeNode parent){
    if(cur.left==null){
        if(cur==root){
            root=cur.right;
        } else if(cur==parent.left){
            parent.left=cur.right;
        } else if(cur==parent.right){
            parent.right=cur.right;
        }
    }else if(cur.right==null){
        if(cur==root){
            root=cur.left;
        } else if(cur==parent.left){
            parent.left=cur.left;
        } else if(cur==parent.right){
            parent.right=cur.left;
        }
    }else{
        TreeNode tp=cur;
        TreeNode target=cur.right;
        while (target.left!=null) {
            tp = target;
            target = target.left;
        }
        cur.val=target.val;
        if(tp.left==target){
            tp.left=target.right;
        }else{
            tp.right=target.right;
        }
    }
}

3. Performance analysis and optimization

Through analysis, we find that both delete and insert operations must be searched before, so the search efficiency represents the performance of these operations of binary search tree

The time complexity of two special search binary trees is analyzed

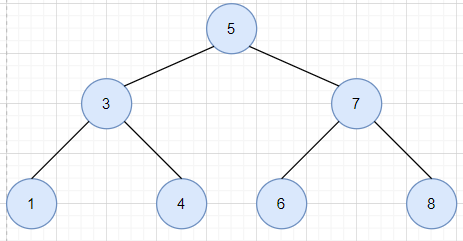
• Complete binary tree (time complexity: O(logN))

• Single branch binary tree (time complexity: O(N))

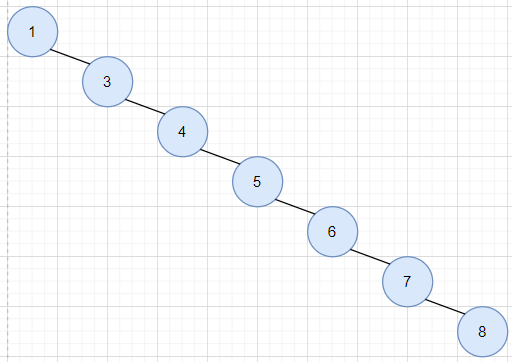
If it is a single tree, the time complexity actually reaches O(N). In order to optimize faster, there are AVL trees and red black trees