next array
definition
- Strict definition: next[i] means the maximum K of the substring s[0...k] == s[i-k...i] (the prefix and suffix can overlap, but not s[0..i]
- Meaning: the subscript of the Prefix suffix such as the longest appearance. If not, it is given - 1
- Graphical explanation: s[0] starts to find a longest substring, which satisfies a condition that when the substring is pulled to the end, it can completely coincide with the parent string
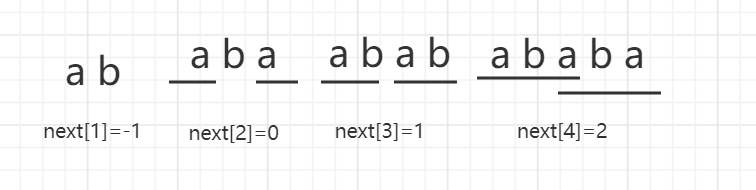
solve
recursion
The above judgment can be summarized as a recursive process:
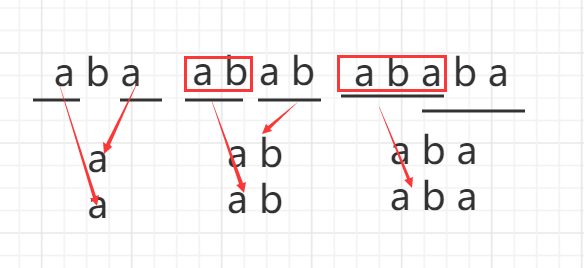
Read two lines of substring, one line provides prefix and the other line provides suffix.
When a new character s[i] is read, the suffix line continues to slide to the left.
If it can be matched, the subscript of the last matching element in the suffix line is the next value
Otherwise, the suffix line slides to the right until an exact match is found
give an example
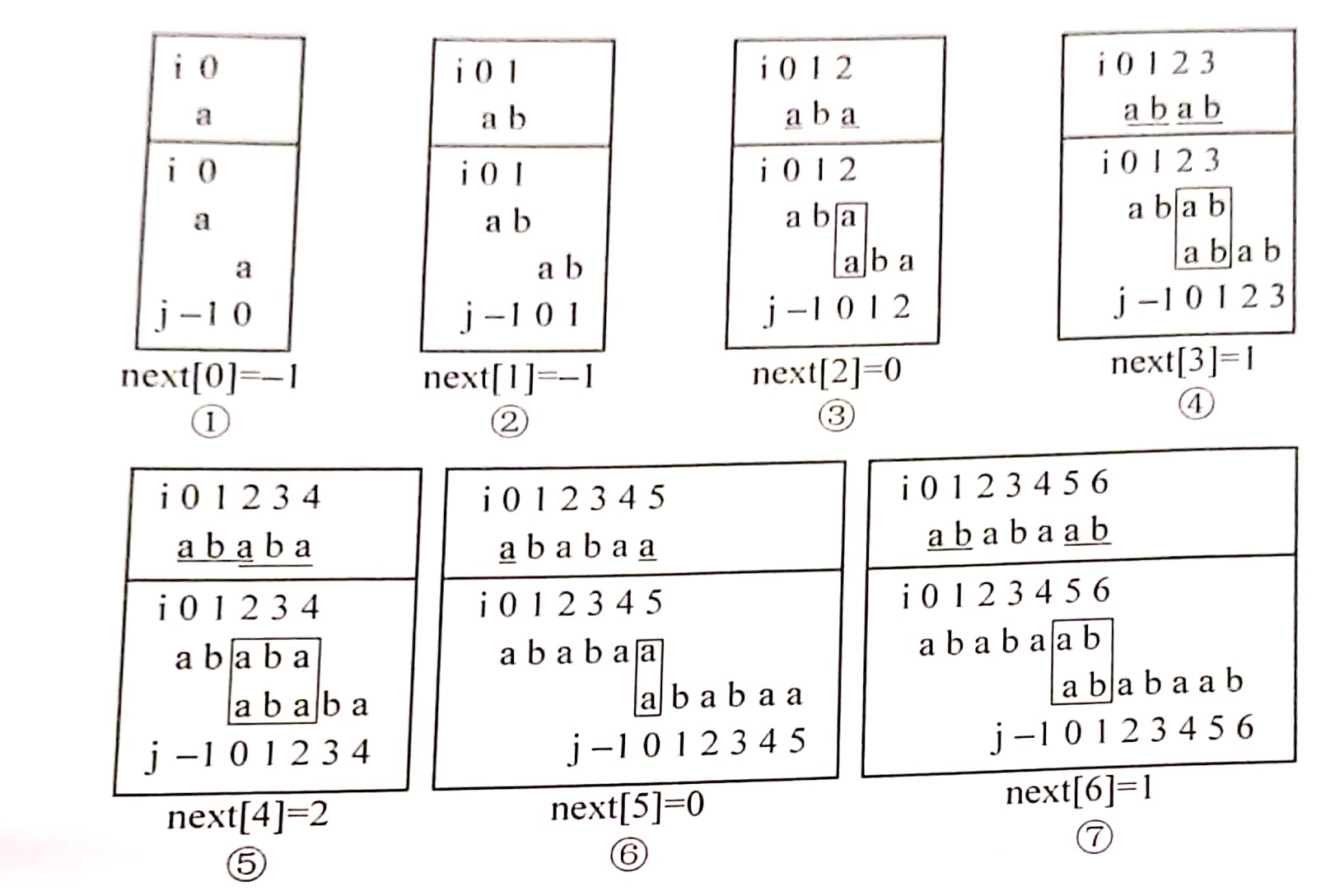
If you know next[0]~next[3], how to recursively find next[4] and next[5]

next[4]:
It is known that next[3]=1. Since s[4]==s[next[3]+1], the prefix of longest phase is extended, and next[4]=next[3]+1
If j=next[3], the above two formulas become s [4] = s [J + 1], and next [4] = j + 1
next[5]:
It is known that next[4]=2, s [5]= S [J + 1] at this time, the Prefix suffix such as the longest phase cannot be expanded. It is necessary to slide the suffix string to a certain position to the right to make it meet "s[5]==s[j+1]", as shown in the rightmost figure of figure 12-3
Now determine j: the essence is to determine~
Since ~ is obtained by sliding "aba" to the right, it is the prefix of aba
Since ~ is also the suffix of "aba", as shown in the rightmost figure of figure 12-3, it can be seen that ~ is the longest prefix of "aba"
"aba" is subscript 0-2 in the suffix line, so j = next[2] (understand it again in combination with the definition of next array) = next[next[4]] = j '(j value when calculating next[4])
Therefore, when solving next[5], just make next[5]=next[2], and then judge whether s[5] == s[j+1] is true
If true, next[5]=next[j]+1
Otherwise, keep j=next[j] until j=-1 or s[5] == s[j+1] is established
realization
step
- Initialize next array, next[0] = j = -1
- Repeat 3.4 for i from 1 - (len-1)
- Keep making j = next[j], know J=- 1 or s[i] == s[j+1],
- If s[i] == s[j+1], next[i] = j+1
code
//getNext solves the next array of string s with length len
void getNext(char s[], int len){
int j = -1;
next[0] = -1; //Initialization j = next[0] = -1
for(int i = 1; i < len; i++){
while(j != -1 && s[i] != s[j+1]){ //Solve next[1] ~ next[len-1]
j = next[j]; //Repeat j = next[j]
} //Until j goes back to - 1, or s[i] == s[j+1]
if(s[i] == s[j+1]){
j++; //Then next[i] = j + 1, shilling J points to this position
}
next[i] = j; //Make next[i] = j
}
}
It is not difficult to find that j is an intermediate variable used to assign a value to next[i] and to record the previous next value in the process of recursive solution (the code uses a loop instead of recursion, but the essence is the idea of recursion)
KMP algorithm
analysis
String matching, matched string: text string text, matched string: pattern string patten
Initialize so that j = - 1 and I = 0.
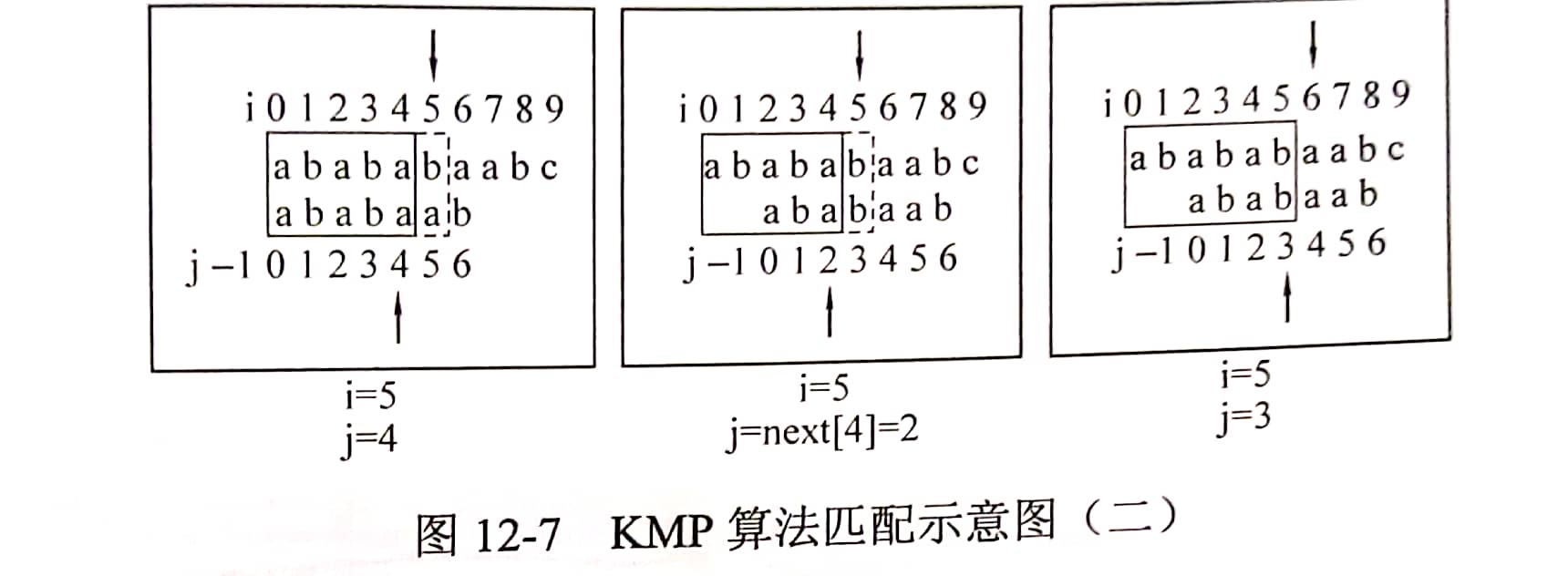
As shown in the following figure, traverse text. When text[i] == patten[j+1], I and j keep moving to the right
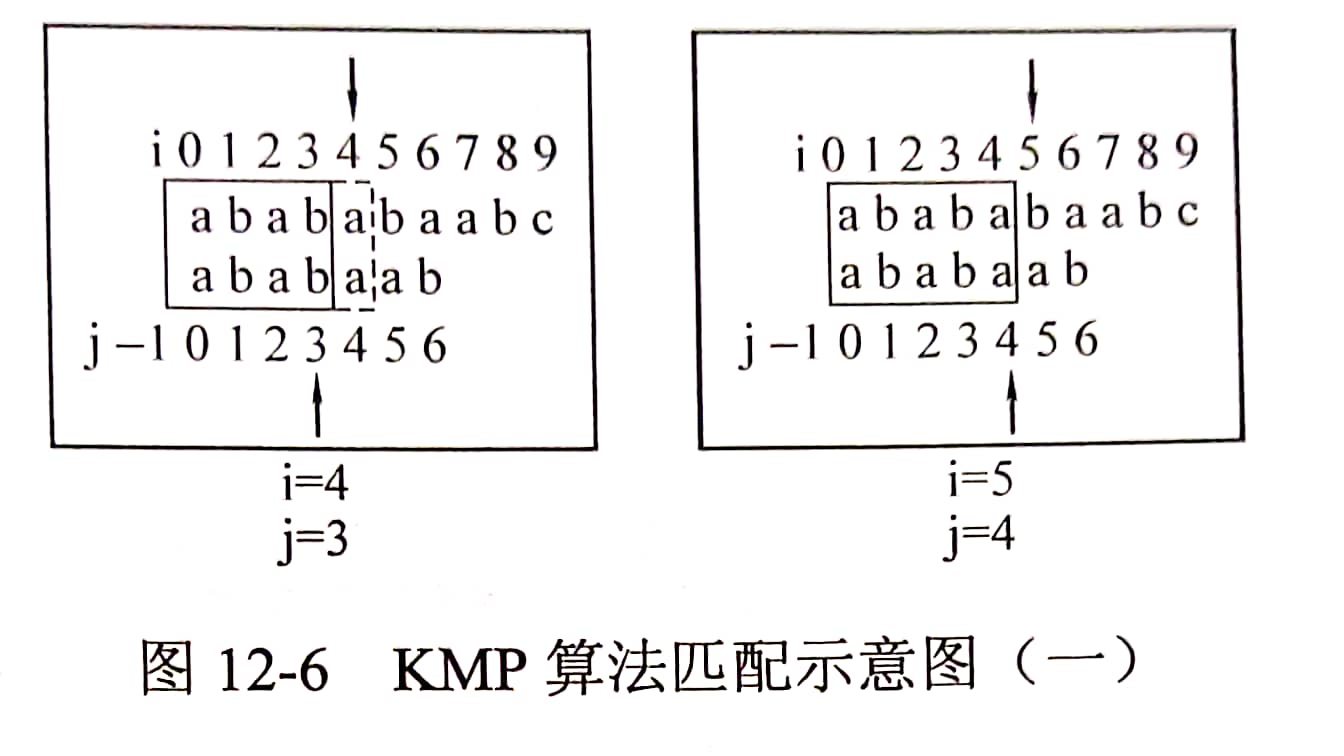
As shown in the following figure, when text [i]= When patten [J + 1], slide patten to the right until the condition text[i] == patten[j+1] is met,
It is not difficult to find that this process is very similar to the mismatch when solving the next array. The same idea as when solving the next array is to make j = next[j], so that patten can quickly move to the corresponding position. It can be seen that next[j] is the position where j should fall back in case of current j mismatch.
Finally, if j == 5 is also matched successfully, it indicates that patten is a substring of text
realization
step
- Initialization j=1
- Let I traverse the text array and execute 3.4. For each I to try to match text[i] and patten[j+1]
- Keep j = next[j] until j == -1 or text[i] == patten[j+1]
- If text[i] == patten[j+1], make j + +; When j== m-1, Patten is a text substring
code
//KMP algorithm to judge whether the pattern array is a substring of text
/*O(m+n)*/
bool KMP(char text[], char patten[]){
int n = strlen(text), m = strlen(patten); //String length
getNext(patten, m); //Calculate the next array of patten
int j = -1; //Initializing j to - 1 indicates that no bit has been matched
for(int i = 0; i < n; i++){ //Attempt to match text[i]
while(j != -1 && text[i] != patten[j+1]){
j = next[j]; //Keep going back until j returns to - 1 or text[i] == patten[j+1]
}
if(text[i] == patten[j+1]){
j++; //text[i] matches patten successfully, make j plus 1
}
if(j == m-1){
return true; //Patten matches exactly, indicating that patten is a substring of text
}
}
return false; //After executing text, the matching is not successful, indicating that patten is not a substring of text
}
Complete code
#include<stdio.h>
#include<string.h>
const int MaxLen = 100;
int next[MaxLen];
//getNext solves the next array of string s with length len
void getNext(char s[], int len){
int j = -1;
next[0] = -1; //Initialization j = next[0] = -1
for(int i = 1; i < len; i++){
while(j != -1 && s[i] != s[j+1]){ //Solve next[1] ~ next[len-1]
j = next[j]; //Repeat j = next[j]
} //Until j goes back to - 1, or s[i] == s[j+1]
if(s[i] == s[j+1]){
j++; //Then next[i] = j + 1, shilling J points to this position
}
next[i] = j; //Make next[i] = j
}
}
//KMP algorithm to judge whether the pattern array is a substring of text
/*O(m+n)*/
bool KMP(char text[], char patten[]){
int n = strlen(text), m = strlen(patten); //String length
getNext(patten, m); //Calculate the next array of patten
int j = -1; //Initializing j to - 1 indicates that no bit has been matched
for(int i = 0; i < n; i++){ //Attempt to match text[i]
while(j != -1 && text[i] != patten[j+1]){
j = next[j]; //Keep going back until j returns to - 1 or text[i] == patten[j+1]
}
if(text[i] == patten[j+1]){
j++; //text[i] matches patten successfully, make j plus 1
}
if(j == m-1){
return true; //Patten matches exactly, indicating that patten is a substring of text
}
}
return false; //After executing text, the matching is not successful, indicating that patten is not a substring of text
}
relationship
The process of solving nex array is the process of pattern string patten self matching