Will share some classic exercises and solutions being done, and write your own understanding if you are interested. If you are interested, you can refer to it.

There are duplicate elements

Given an integer array, determine whether there are duplicate elements.
If a value exists and appears in the array at least twice, the function returns true. Returns false if each element in the array is different.
Example 1:

Input:[1, 2, 3, 1]
Output: true

Example 2:

Input:[1, 2, 3, 4]
Output: false

Example 3:

Input:[1,1,1,3,3,4,3,2,4,2]
Output: true

Official answer:

class Solution {
public:
    bool containsDuplicate(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        for(int i = 0; i < n-1; i++)
        {
            if(nums[i+1] == nums[i])
            {
                return true;
            }
        }
        return false;
    }
};

When I write it myself, I change if (Num [i + 1] = = num [i]) to if (Num [i] = = num [I-1]) and report an error directly
Line 1034: Char 34: runtime error: addition of unsigned offset to 0x602000000090 overflowed to 0x60200000008c (stl_vector.h)
After thinking about it, there is a problem with writing like this. There are no other elements in front of the element in bit 0.

Maximum suborder sum

Given an integer array nums, find a continuous sub array with the largest sum (the sub array contains at least one element) and return its maximum sum.
Example 1:

Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
 Explanation: continuous subarray [4,-1,2,1] The sum of is 6.

Example 2:

Input: nums = [1]
Output: 1

Example 3:

	Input: nums = [0]
	Output: 0

Example 4:

Input: nums = [-1]
Output:-1

Example 5:

Input: nums = [-100000]
Output:-100000

This article mainly discusses the greedy method to solve this problem:
The idea of greedy algorithm: if the sum of the elements indicated by the current pointer is less than 0, the elements before the pointer will be discarded.

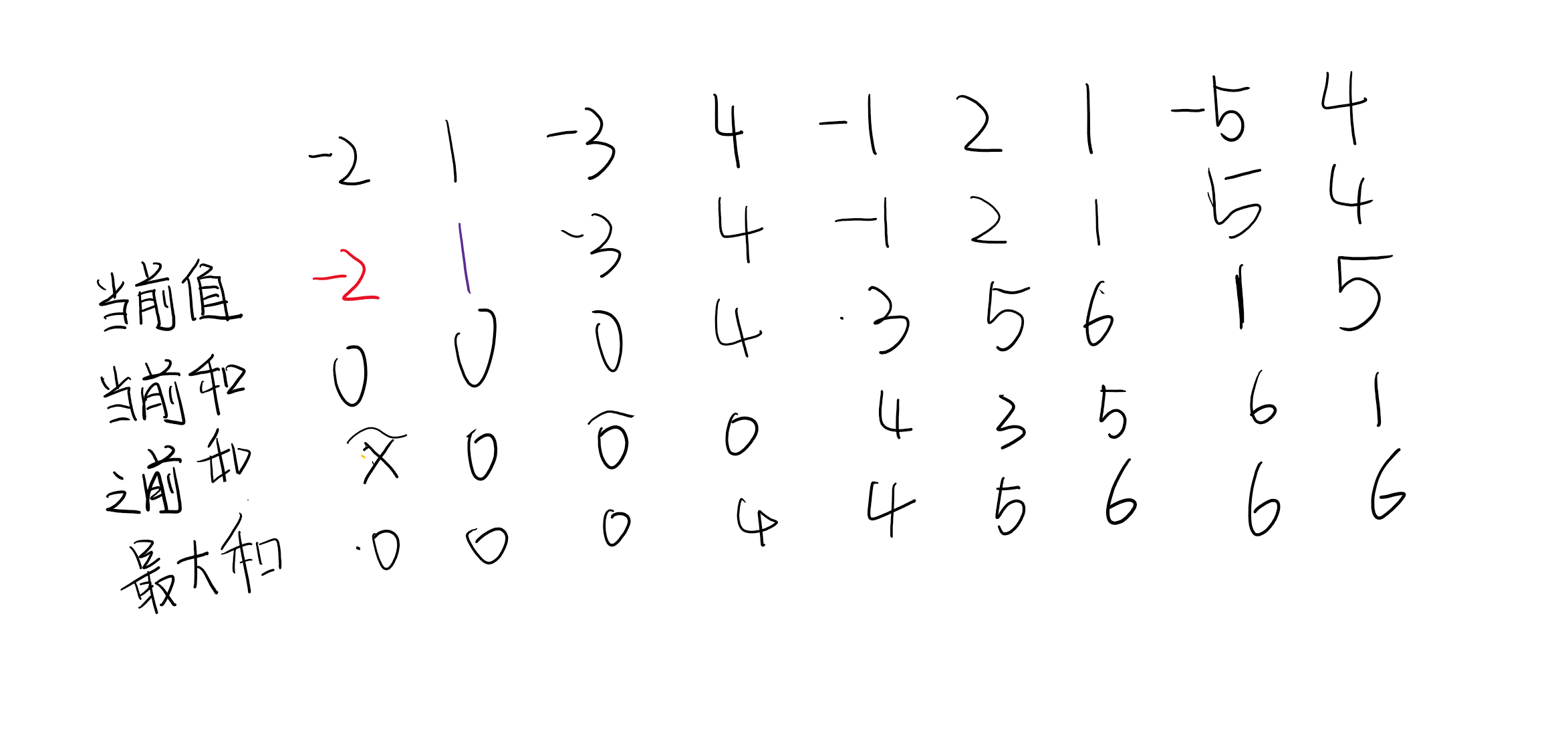
We can use the way of drawing to preliminarily conclude that the maximum sum is 6 and the maximum sum suborder is [4, - 1, 2, 1].
The following is the code implementation

	class Solution {
public:
    int maxSubArray(vector<int>& nums) {
       int result = nums[0];  /Initialization maximum sum is nums The first element of the array
       int sum = 0;	/Initializes the current and, in this case, 0 sum Minimum boundary of value
       int numsize = nums.size();  /obtain nums The size of the array
       for( int i = 0; i<numsize; i++){ 
           sum+= nums[i];
           result =max(result, sum);  /Compare current sum Value and maximum result Select maximum value
           if(sum<0)
           {
               sum = 0; /sum If the value is less than 0, discard it directly
           }
       }
    return result;
   }
};

Sum of two numbers

Given an integer array nums and an integer target value target, please find the two integers with and as the target value target in the array and return their array subscripts.

You can assume that each input will correspond to only one answer. However, the same element in the array cannot be repeated in the answer.

You can return answers in any order.

My level is only enough to do the first question 💔.
However, it still takes two traversals, and the time complexity is O(n^2). Because the topic is relatively simple, there is no more to expand.

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
       int n = nums.size();
        for(int i = 0; i < n-1; i++)
        {
            for(int j = i+1; j< n; j++){
                if(nums[i] + nums[j] == target)
                {
                   return {i, j};
                }
            }
        }
        return {};
    }
};

Merge two ordered arrays

Here are two ordered integer arrays nums1 and nums2. Please merge nums2 into nums1 to make nums1 an ordered array.

The number of elements initializing nums1 and nums2 is m and n, respectively. You can assume that the space size of nums1 is equal to m + n, so it has enough space to store elements from nums2.
In fact, this problem is not difficult, because it has been assumed that the space of nums1 has n+m. in this way, the elements of num2 can be directly inserted into num1 and sorted.
The specific implementation code is as follows

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
                for(int i =0; i<= n-1; i++)
                {
                    nums1[m+i] = nums2[i];
                }
        sort(nums1.begin(), nums1.end());
    }
};

ps: after finishing the problem, I read Xiali buckle's machine learning 101. I feel it's really useless 23333.

Intersection of two arrays

Given two arrays, write a function to calculate their intersection.
Example 1:

Input: nums1 = [1,2,2,1], nums2 = [2,2]
Output:[2,2]

Example 2:

Input: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
Output:[4,9]

The number of occurrences of each element in the output result shall be consistent with the minimum number of occurrences of elements in the two arrays.
We can ignore the order of the output results.
The code implementation is as follows:

	class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        vector<int> num;
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        int length1 = nums1.size();
        int length2 = nums2.size();
        int index1 = 0, index2 = 0;
        while(index1 < length1 && index2 < length2)
        {
            if(nums1[index1]< nums2[index2])
            {
                index1++;
            }
            else if(nums1[index1]> nums2[index2])
            {
                index2++;
            }
            else {
                num.push_back(nums1[index1]);
                index1++;
                index2++;
            }
        }
        return num;
    }
};

Two methods are used in the force buckle, namely hash table and double pointer. When I solve the problem, I use the double pointer writing method. Explain that it's actually sorting first, and then whoever is younger runs first.