Line Segment Tree (A Binary Search Tree)

The characteristics of tree structure make it more convenient to query and search.
Line segment tree is convenient for querying and updating the interval, because the father node on the tree represents an interval. The node of the leaf is the original element.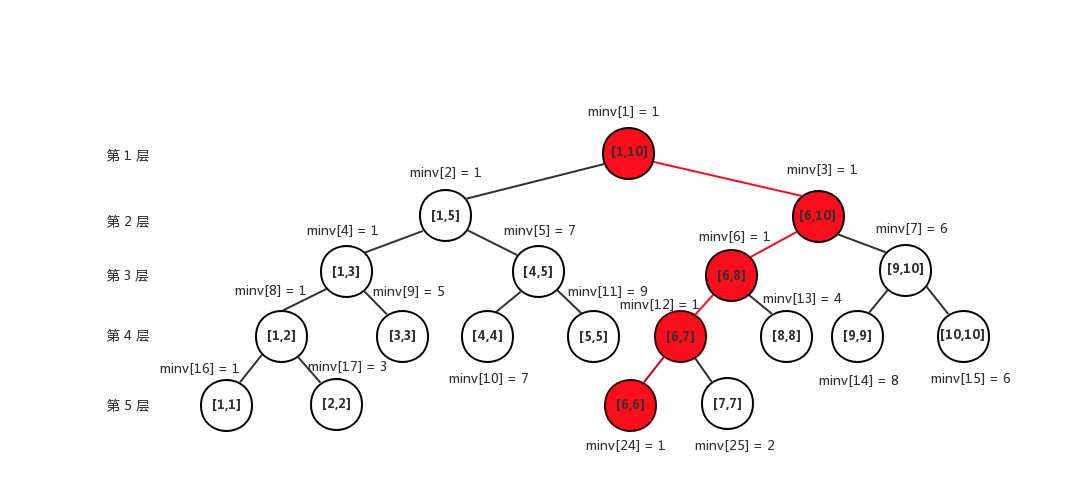

As shown in the figure above:

The steps to solve the problem by using segment tree are as follows (take template questions - give N numbers, and find any interval combination as an example):

For this algorithm, I think it is necessary to understand: 1. When building a tree, how to traverse the whole tree and deal with nodes as intervals and sums. 2. Use lazy tags to add data to the tree when maintaining intervals, and how to press the lazy tags of nodes into the nodes below when needed. 3. How to press the lazy tag of the node into the node below when needed when querying the interval.
Above is the essence of the algorithm, general access.

Details are as follows

//Pre-processing data and main functions to facilitate subsequent reading of the code. p [] array stores input data, tr [N < 2] stores node values and lazy tags.
const int N=1e5+5;
int p[N];
struct node{
    long long sum,lazy;
}tr[N<<2];
int main()
{
    int n,m,i,k,a,b,q;
    scanf("%d%d",&n,&m);                          //Input n digits, m processing
    for(i=1;i<=n;i++){
        scanf("%d",&p[i]);
    }
    build_tree(1,1,n);
    while(m--){
        scanf("%d",&q);
        if(q==1){                                              //1 represents interval plus k value
            scanf("%d%d%d",&a,&b,&k);
            add(1,1,n,a,b,k);
        }
        else{                                               //2 represents the sum of queries a to b
            scanf("%d%d",&a,&b);
            printf("%lld\n",search_tree(1,1,n,a,b));
        }
    }
    return 0;
}

1. Using the relationship in the title to build a tree, using DFS, recursively traverse every point of the tree, which mainly involves recursive backtracking, all of which are traversed;
The code is as follows:

    void update(int root)
{
    tr[root].sum=tr[root<<1].sum+tr[root<<1|1].sum;     //Add the left and right son nodes to the father node. That's what intervals mean.
}
void build_tree(int root, int l, int r)
{
    if(l==r){
        tr[root].sum=p[l] ;                  //Satisfying conditions (traversing to leaf nodes)
        return;
    }
    int mid=(l+r)>>1;
    build_tree(root<<1,l,mid);                    //Diversion, left son;
    build_tree(root<<1|1,mid+1,r);              //Diversion, right son;
    update(root);                                       //Pass to Father Node
}

If you haven't learned dfs, you will understand it better, but a picture can make you happy!

2. The following is the maintenance of the interval. The maintenance of the interval reflects the advantages of the line segment tree naked. Every query only needs to find the location of the father node which satisfies the left and right intervals. With the lazy tag, the time required is greatly reduced.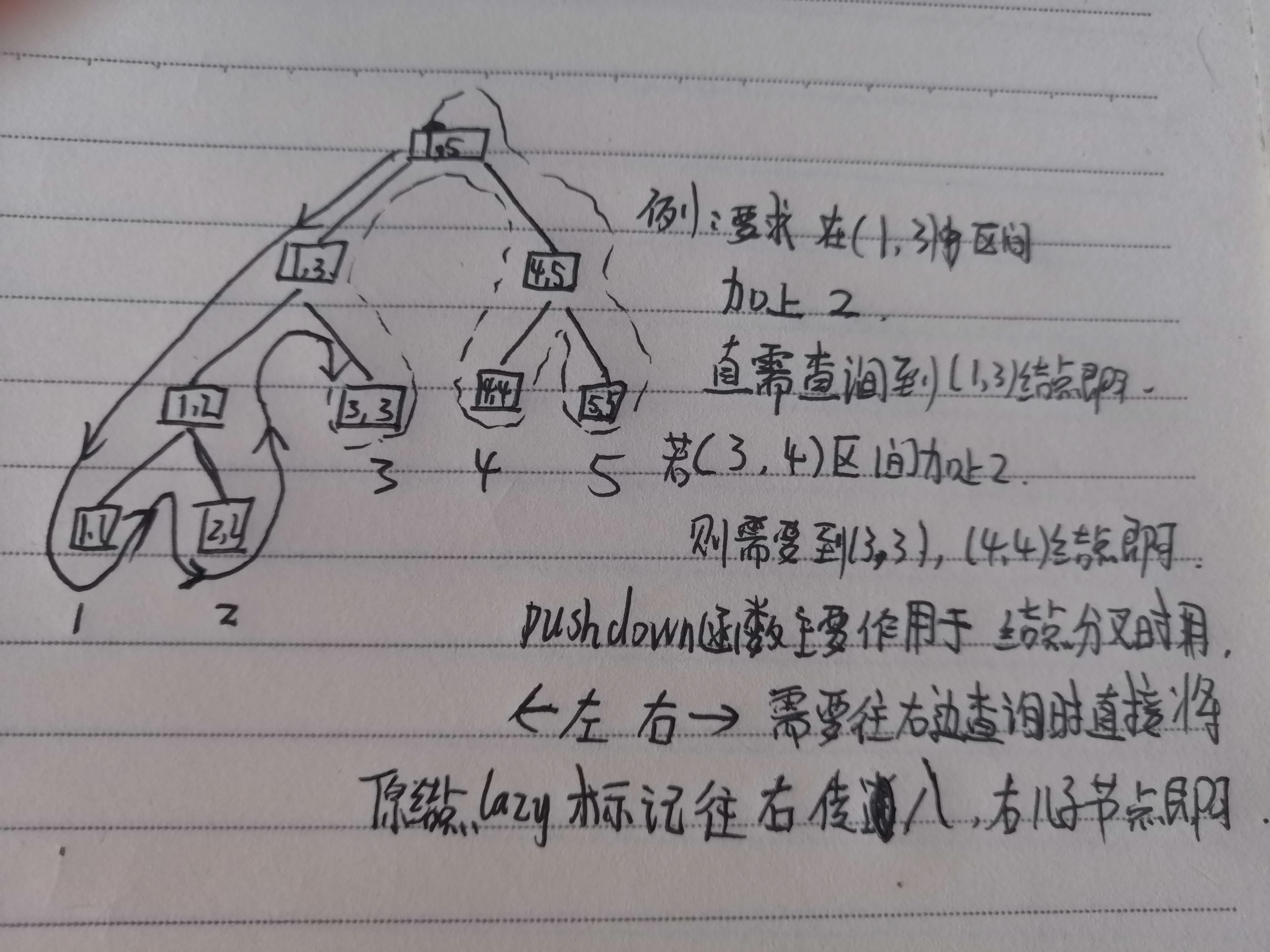

The code is as follows:

void pushdown(int root, int l, int r)      //The pushdown function pushes the lazy value of the original node into the left and right sons
{
    if(!tr[root].lazy) return;            //A kind of pruning, good.
    int mid=(l+r)>>1;
    tr[root<<1].sum+=(tr[root].lazy*(mid-l+1));  //Update the sum of the left son node
    tr[root<<1|1].sum+=(tr[root].lazy*(r-mid));  //Update the sum of the right son node
    tr[root<<1].lazy+=tr[root].lazy;             //Update the left son node lazy tag
    tr[root<<1|1].lazy+=tr[root].lazy;            //Update the right son node lazy tag
    tr[root].lazy=0;                           //Zero the lazy tag of the parent node
}
void add(int root, int l, int r, int a, int b, int k)
{
    if(l==a&&r==b){            //Finding the target node region
        tr[root].lazy+=k;       //To update  
        tr[root].sum+=k*(l-r+1);  //To update
        return ;
    }
    pushdown(root,l,r);     // Each time, check whether the father node needs to be pushed into the left and right nodes.
    int mid=(l+r)>>1;
    if(mid>=b){               //  Need to go to the left interval
        add(root<<1,l,mid,a,b,k); 
    }
    else if(mid<a){        //  Need to go to the right interval
        add(root<<1|1,mid+1,r,a,b,k);
    }
    else{               // Both left and right intervals need to be looked for.
        add(root<<1,l,mid,a,mid,k);
        add(root<<1|1,mid+1,r,mid+1,b,k);
    }
    update(root);     //The father node also needs to be updated.
}

3. Query interval sum; (This point is similar to the above interval maintenance, mainly interval query, the difference is to return the value of the interval)
The code is as follows:

long long search_tree(int root, int l, int r, int a, int b)
{
    if(l==a&&r==b){
        return tr[root].sum;
    }
    pushdown(root,l,r);     // Whether the father node needs to be pressed into the child node is checked every time.
    int mid=(l+r)>>1;       
    if(mid>=b){
        return search_tree(root<<1,l,mid,a,b);   //Returning the value found is also a recursive implementation.
    }
    else if(mid<a){
        return search_tree(root<<1|1,mid+1,r,a,b);
    }
    else{
        return search_tree(root<<1,l,mid,a,mid)+search_tree(root<<1|1,mid+1,r,mid+1,b);
    }
}

The main purpose of learning this algorithm is to understand recursive implementation thoroughly, lazy marking thoroughly, line segment tree thoroughly, interval interval????? No can no bibi bi!! < ->

Patience works wonders

The code is too long to recommend chunking.

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=1e5+5;
int p[N];
struct node{
    long long sum,lazy;
}tr[N<<2];
void update(int root)
{
    tr[root].sum=tr[root<<1].sum+tr[root<<1|1].sum;
}
void build_tree(int root, int l, int r)
{
    if(l==r){
        tr[root].sum=p[l];
        return;
    }
    int mid=(l+r)>>1;
    build_tree(root<<1,l,mid);
    build_tree(root<<1|1,mid+1,r);
    update(root);
}
void pushdown(int root, int l, int r)
{
    if(!tr[root].lazy) return;
    int mid=(l+r)>>1;
    tr[root<<1].sum+=(tr[root].lazy*(mid-l+1));
    tr[root<<1|1].sum+=(tr[root].lazy*(r-mid));
    tr[root<<1].lazy+=tr[root].lazy;
    tr[root<<1|1].lazy+=tr[root].lazy;
    tr[root].lazy=0;
}
void add(int root, int l, int r, int a, int b, int k)
{
    if(l==a&&r==b){
        tr[root].lazy+=k;
        tr[root].sum+=k*(l-r+1);
        return ;
    }
    pushdown(root,l,r);
    int mid=(l+r)>>1;
    if(mid>=b){
        add(root<<1,l,mid,a,b,k);
    }
    else if(mid<a){
        add(root<<1|1,mid+1,r,a,b,k);
    }
    else{
        add(root<<1,l,mid,a,mid,k);
        add(root<<1|1,mid+1,r,mid+1,b,k);
    }
    update(root);
}
long long search_tree(int root, int l, int r, int a, int b)
{
    if(l==a&&r==b){
        return tr[root].sum;
    }
    pushdown(root,l,r);
    int mid=(l+r)>>1;
    if(mid>=b){
        return search_tree(root<<1,l,mid,a,b);
    }
    else if(mid<a){
        return search_tree(root<<1|1,mid+1,r,a,b);
    }
    else{
        return search_tree(root<<1,l,mid,a,mid)+search_tree(root<<1|1,mid+1,r,mid+1,b);
    }
}
int main()
{
    int n,m,i,k,a,b,q;
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++){
        scanf("%d",&p[i]);
    }
    build_tree(1,1,n);
    while(m--){
        scanf("%d",&q);
        if(q==1){
            scanf("%d%d%d",&a,&b,&k);
            add(1,1,n,a,b,k);
        }
        else{
            scanf("%d%d",&a,&b);
            printf("%lld\n",search_tree(1,1,n,a,b));
        }
    }
    return 0;
}

Thank you for watching. Just collect if you like.