Learning materials

1. Monotone Queue and Its Application By Codinginging
2. Monotonic queue By liukee
3. Initial monotone queue By justmeh
4. Monotone stack-monotone team in the door By _tham

Example

Consolidated fruit

luogu1090

Topic Description

In an orchard, Doudou has knocked down all the fruits and divided them into different heaps according to different kinds of fruits. Dodo decided to put all the fruits together.

Every merger, more than two piles of fruit can be merged together, the physical expenditure is equal to the sum of the weight of two piles of fruit. It can be seen that after n-1 mergers of all the fruits, there is only one pile left. The total amount of physical energy consumed in merging fruits is equal to the sum of physical energy consumed in each merger.

Because it takes a lot of effort to move these fruits home, it is necessary to save as much energy as possible when combining the fruits.

Assuming that the weight of each fruit is 1, and the number of types and fruits of each fruit is known, your task is to design a merged sequencing scheme to minimize the amount of physical energy consumed and output the minimum value of physical energy expenditure.

For example, there are three kinds of fruits, the number of which is 1, 2, 9 in turn. First, 1 and 2 heaps can be merged, the number of new heaps is 3, and the energy consumption is 3. Then, the new reactor is merged with the original third reactor, and a new reactor is obtained, the number of which is 12 and the physical cost is 12. So the total physical cost is 3 + 12 = 15. It can be proved that 15 is the minimum physical cost.

input
The input consists of two lines. The first line is an integer n (1<=n<=10000), representing the number of fruits. The second line contains n integers separated by spaces, and the first integer AI (1<=ai<=20000) is the number of the first fruit.

output
The output consists of one line, which contains only one integer, the minimum physical cost. Enter data to ensure that the value is less than 2 ^ 31.

Input and Output Samples

Input #1 replication
3
1 2 9
Output #1 replication
1
Note/hint
For 30% of the data, it is guaranteed that n is less than 1000:

For 50% of the data, n < 5000 is guaranteed.

For all data, it is guaranteed that n is less than 10000.

Analysis

See my blog: Luogu 1090 Combines Fruits

Code

/************************
User:Mandy.H.Y
Language:c++
Problem:luogu1090
Algorithm:  
************************/
#include<bits/stdc++.h>

using namespace std;

const int maxn = 1e4 + 5;

int n,l1,r1,l2,r2;
long long ans;
long long q[maxn],a[maxn];

template<class T>inline void read(T &x){
    x = 0;bool flag = 0;char ch = getchar();
    while(!isdigit(ch)) flag |= ch == '-',ch =  getchar();
    while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch =  getchar();
    if(flag) x = -x;
}

template<class T>void putch(const T x){
    if(x > 9) putch(x / 10);
    putchar(x % 10 | 48);
}

template<class T>void put(const T x){
    if(x < 0) putchar('-'),putch(-x);
    else putch(x);
}

void file(){
	freopen("testdata(1).in","r",stdin);
//	freopen("1090.out","r",stdin);
}

void readdata(){
	read(n);
	for(int i = 1;i <= n; ++ i){
		read(a[i]);
	}
}

void work(){
		l1 = 1,r1 = n + 1;
	sort(a + 1,a + 1 + n);
	l2 = r2 = 0;
	for(int i = 1;i < n; ++ i){
		long long x1,x2,x3,x4,x = 0;
		if(l1 < r1) x1 = a[l1];
		else x1 =1e15;
		if(l1 < r1-1) x2 = a[l1 + 1];
		else x2 = 1e15;
		if(l2 < r2) x3 = q[l2];
		else x3 =1e15;
		if(x3 > x1){
			x += x1;l1++;
			if(x3 > x2) x+=x2,l1++;
			else x += x3,l2++;
		}else{
			x += x3;l2++;
			if(l2 < r2) x4 = q[l2];//Here l2 has + 
			else x4 = 1e15;
			if(x4 < x1) x += x4,l2++;
			else x += x1,l1++;
		}
		q[r2++] = x;
		ans += x;
	}
	put(ans);
}

int main(){
//	file();
	readdata();
	work();
	return 0;
}

sliding window

luogu1886
Topic Description
Now there's a bunch of numbers (N<=10^6) and a window of size k. Now this slides from the left to the right, one unit at a time, and finds the maximum and minimum values in the window after each sliding.

For example:

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

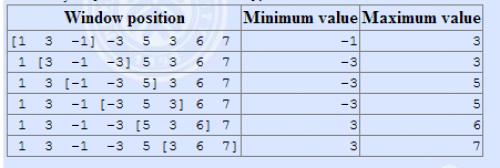
Input format
There are two lines of input, the first action n,k.

Number of second actions n (< INT_MAX).

Output format
The output consists of two lines. The first action is the minimum value of each window sliding.

The second action is the maximum value of each window sliding

Input and Output Samples
Input #1 replication
8 3
1 3 -1 -3 5 3 6 7
Output #1 replication
-1 -3 -3 -3 3 3
3 3 5 5 6 7
Note/hint
50% of the data, n <== 10 ^ 5

100% data, n <=10^ 6

Analysis

See my blog: luogu 1886 Sliding Window

Code

//1886 Sliding Window 
#include<bits/stdc++.h>
using namespace std;

const int maxn=1e6+5;

int n,k,a[maxn],q[maxn],l,r; 

void readdata()
{
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
}

void init()
{
    freopen(".txt","r",stdin);
    freopen(".txt","w",stdout);
}

void work()
{
    l=r=0;
    for(int i=1;i<=n;i++)
    {
        while(l<r && a[q[r-1]]>=a[i]) r--;
        q[r++]=i;
        while(l<r && q[l]<i-k+1) l++;
        if(i>=k) printf("%d ",a[q[l]]);
    }
    printf("\n");
    l=r=0;
    for(int i=1;i<=n;i++)
    {
        while(l<r && a[q[r-1]]<=a[i]) r--;
        q[r++]=i;
        while(l<r && q[l]<i-k+1) l++;
        if(i>=k) printf("%d ",a[q[l]]);
    }
}

int main()
{
    //init();
    readdata();
    work();
    return 0;
}

Finding the Minimum Value in m Interval

luogu1440

Topic Description
A sequence of numbers containing n terms (n<=2000000) is used to find the minimum number of M before each term in its interval. If the preceding number is less than m, it starts with the first number and outputs 0 if there is no preceding number.

Input format
The first row has two numbers n and m.

The second row, n positive integers, is a given sequence of numbers.

Output format
Line n, the number ai of line i, is the minimum of the number m before the number I in the sequence.

Input and Output Samples
Input #1 replication
6 2
7 8 1 4 3 2
Output #1 replication
0
7
7
1
1
3
Note/hint
[Data Scale]

m≤n≤2000000

ai​≤3×10^7

Analysis

See my blog: luogu 1440 to find the minimum value in m interval

Code

/**************************
User:Mandy.H.Y
Language:c++
Problem:luogu1440
Algorithm:
**************************/
#include<bits/stdc++.h>

using namespace std;

const int maxn = 2e6 + 5;

int n,l,r,m;
int q[maxn],a[maxn];

template<class T>inline void read(T &x){
    x = 0;bool flag = 0;char ch = getchar();
    while(!isdigit(ch)) flag |= ch == '-',ch = getchar();
    while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar();
    if(flag) x = -x;
}

template<class T>void putch(const T x){
    if(x > 9) putch(x / 10);
    putchar(x % 10 | 48);
}

template<class T>void put(const T x){
    if(x < 0) putchar('-'),putch(-x);
    else putch(x);
}

void file(){
    freopen("1440.in","r",stdin);
    freopen("1440.out","w",stdout);
}

void readdata(){
    read(n);read(m);
}

void work(){
    for(int i = 1;i <= n; ++ i){
        
        read(a[i]);
        
        while(l < r && i - q[l] > m) l++;
        
        if(l >= r) puts("0");
        else put(a[q[l]]),putchar('\n');
        
        while(l < r && a[q[r - 1]] >= a[i]) r--;//>= 
        q[r++] = i;
    }
}

int main(){
//    file();
    readdata();
    work();
    return 0;
}

Cut the cake

luogu1714

Topic Description
Today is Xiao Z's birthday. His classmates brought him a cake. This cake is a cuboid, divided into N identical pieces in different colors, each piece has its corresponding lucky value.

As a longevity star, small Z naturally wishes to eat the greatest sum of lucky value of the first cake, but small Z can only eat M pieces (M < N) of cake at most.

It's natural that little Z doesn't want to think about eating. So little Z throws this task to you who learns OI. Please help him find out the continuous K cakes (k < M) from these N cakes so as to maximize the lucky value on them.

Input format
The first line of the input file cake.in is two integers N,M. Represents a total of N pieces of cake, small Z can only eat M pieces at most.

The second line contains N integers separated by spaces, and the first integer Pi represents the lucky value of the second cake.

Output format
The output file cake.out has only one line, an integer, which is the maximum lucky value that small Z can get.

Input and Output Samples
Input #1 replication
5 2
1 2 3 4 5
Output #1 replication
9
Input #2 replication
6 3
1 -2 3 -4 5 -6
Output # 2 replication
5
Note/hint
For 20% of the data, N is less than 100.

For 100% of the data, N is less than 500000, | Pi | is less than 500. The answer is guaranteed to be within 2 ^ 31 - 1.

Analysis

See my blog: luogu 1714 Cut Cake

Code

/**************************
User:Mandy.H.Y
Language:c++
Problem:luogu1440
Algorithm:
**************************/
#include<bits/stdc++.h>

using namespace std;

const int maxn = 5e5 + 5;

int n,l,r,m;
long long ans = -1e15;
int q[maxn],a[maxn];

template<class T>inline void read(T &x){
    x = 0;bool flag = 0;char ch = getchar();
    while(!isdigit(ch)) flag |= ch == '-',ch = getchar();
    while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar();
    if(flag) x = -x;
}

template<class T>void putch(const T x){
    if(x > 9) putch(x / 10);
    putchar(x % 10 | 48);
}

template<class T>void put(const T x){
    if(x < 0) putchar('-'),putch(-x);
    else putch(x);
}

void file(){
    freopen("1440.in","r",stdin);
    freopen("1440.out","w",stdout);
}

void readdata(){
    read(n);read(m);
}

void work(){
    //Prefix and 
    for(int i = 1; i <= n ; ++ i){
        read(a[i]);a[i] += a[i - 1];
        while(l < r && i - q[l] > m) l++;
        //Here I - Q [l] > m, because a[i] - a[j-1] is the sum of J to I 
//        Ans = max (ans, (long) a[i]; no, a[i] is prefix and 
        ans = max(ans,(long long)a[i] - a[q[l]]);
        while(l < r && a[q[r-1]] >= a[i]) r--;//>=
        q[r++]  = i;
    }
    put(ans);
}

int main(){
//    file();
    readdata();
    work();
    return 0;
}

Largest Rectangle in a Histogram

POJ 2559

Analysis

Topic translation and problem solving: POJ 2559 Largest Rectangle in a Histogram

Code

/************************
User:Mandy.H.Y
Language:c++
Problem:POj 2559
Algorithm:  
************************/
//#include<bits/stdc++.h>
#include<cstdio>
#include<iomanip> 
#include<cmath> 

using namespace std;

const int maxn = 1e5 + 5;

int n,l,r;
int q[maxn];

struct Node{
	int h,l,r;
}node[maxn]; 

template<class T>inline void read(T &x){
    x = 0;bool flag = 0;char ch = getchar();
    while(!isdigit(ch)) flag |= ch == '-',ch =  getchar();
    while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch =  getchar();
    if(flag) x = -x;
}

template<class T>void putch(const T x){
    if(x > 9) putch(x / 10);
    putchar(x % 10 | 48);
}

template<class T>void put(const T x){
    if(x < 0) putchar('-'),putch(-x);
    else putch(x);
}

void file(){
	freopen("2559.in","r",stdin);
//	freopen("1090.out","r",stdin);
}

void work(){
	read(n);
	while(n){
		long long ans = 0;
		for(int i = 1;i <= n; ++ i) read(node[i].h),node[i].l = i,node[i].r = i;
		//Initialize l, r 
		l = r = 0;
		for(int i = 1;i <= n; ++ i){
			while(l < r && node[q[r - 1]].h >= node[i].h) node[i].l = node[q[r - 1]].l,r--;
			//Q contains a number, node [i]. L = node [q [r - 1]. l, or the remaining coordinate + 1, but to be empty 
			q[r++] = i;
		}
		l = r = 0;
		for(int i = n; i >= 1; -- i){
			while(l < r && node[q[r - 1]].h >= node[i].h) node[i].r = node[q[r - 1]].r,r--;
			q[r++] = i;
			ans = max(ans,(long long)node[i].h * (node[i].r - node[i].l + 1));
		}
		put(ans);
		putchar('\n');
		read(n);
	}
}

int main(){
//	file();
	work();
	return 0;
}