1, Double linked list

There is only one pointer to its successor in the single linked list node, so that the single linked list can only traverse backward from the first node in turn.

To access the predecessor node of a node (during insertion and deletion operations), you can only traverse from the beginning. The time complexity of accessing the successor node is 0 (1), and the time complexity of accessing the predecessor node is O(n).

In order to overcome the above shortcomings of single linked list, double linked list is introduced. The double linked list node has two pointers, prior and next, pointing to its predecessor node and successor node respectively.

1.1 storage definition of double linked list:

typedef struct DuLNode{
	ElemType data;	// Data domain
	struct DuLNode *prior,*next;  // Predecessor and successor pointers
}DNode,*DlinkList

The double linked list adds a prior pointer to its predecessor in the node of the single linked list, so the operations of search by value and search by bit in the double linked list are the same as those in the single linked list. However, the implementation of insertion and deletion of double linked list is quite different from that of single linked list.

1.2 initialization of double linked list:

bool InitDLinklist(DlinkList l&){
    L = (DNode *)malloc(sizeof(DNode)); // Allocation header node
    if(L==NULL)     // Insufficient memory, allocation failed
        return false;
    L->prior = NULL;  // The prior ity of the header node always points to NULL
    L->next = NULL;   // There is no node after the head node
    return true;
}

1.3 empty judgment of double linked list:

bool Empty(DlinkList L){
    if(L->next==NULL)
        return true;
    else
        return false;
}

1.4 search operation of double linked list:

Find the ith element in the bidirectional linked list L of the leading node and return the address of the node.

DNode *GetElemP_DuL(DlinkList L, int i) {	
//Find the ith element in the two-way linked list L of the leading node and return the address of the node
	int j;
	DlinkList p;
	p = L->next;
	j = 1; //Initialization, p points to the first node, and j is the counter
	while (j<i&&p) { // Loop until p points to the ith element or p is empty
		p = p->next;
		++j;
	}
	if (!p||j>i)
		return NULL; // The ith element does not exist
	return p;
}

1.5 insertion of double linked list:

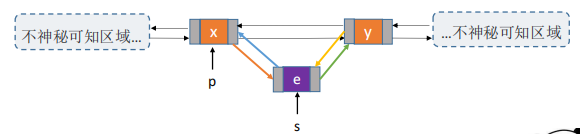
Determine the position pointer p of the ith element in L and insert it forward or backward.
[analysis]: circular operation: determine the legal position pointer p of the ith element in L; Then create the s node and assign e to the data field of S.

• Sufficient conditions: 1. The next node of P is the next node of S; 2. The precursor of the next node of P is the s node; Therefore – > 3, s's (predecessor) previous node is p, and P's (successor) next node is s.

• Pre insert at position i: sufficient conditions: 1. The previous node of P is the previous node of S; 2. The last node of P is followed by s node; Therefore, the (subsequent) node of – > 3 and S is p, and the (predecessor) node of P is s.

1,Post insert core code:
s = new DNode; // Generate new node * s
s->data = e; // Set the node * s data field to e
s->next = p->next;
p->next->prior = s;
s->prior = p;
p->next = s;
++length;
----
2,Pre inserted core code:
s = new DNode; // Generate new node * s
s->data = e; // Set the node * s data field to e
s->prior = p->prior;
p->prior->next = s;
s->next = p;
p->prior = s;
++length;
----
3,Insert on the first element of the two-way linked list
if(i==1){
    s = new DNode;
    s->data = e;
    DlinkList p = L->next;
    L->next = s;
    s->prior = L;
    s->next = p;//Insert node * s into L
	p->prior = s;    
    ++length;
}
----
4,Insert on the last element of the bidirectional linked list
else if (i == length) { //Insert on the last element of the bidirectional linked list
	s = new DNode; //Generate new node s
	s->data = e; //Set node s data to e
	DlinkList p = L;
	while (p->next)
		p = p->next; // Point the LinkList p to the end of the bidirectional linked list
	p->next = s;
	s->prior = p; // Insert node * s after p and into L
	s->next = NULL;
	++length;

Algorithm insertion of bidirectional linked list: insert element e before the ith position in the bidirectional linked list L of the leading node, and the legal value of i is 1 < = i < = table length + 1.

Status ListInsert_DuL(DlinkList &L, int i, ElenType e) { //Insertion algorithm of bidirectional linked list
	DlinkList s, p;
	if (!(p = GetElemP_DuL(L, i))) //Determine the position pointer p of the ith element in L
		return ERROR; //When p is NULL, the ith element does not exist
	if (i == 1) {//Insert on the first element of the two-way linked list
		s = new DNode; //Generate new node s
		s->data = e; //Set node s data to e
		DlinkList p = L->next;
		L->next = s;
		s->prior = L;
		s->next = p;//Insert node * s into L
		p->prior = s;
		++length;
	} else if (i == length) {//Insert on the last element of the bidirectional linked list
		s = new DNode; //Generate new node s
		s->data = e; //Set node s data to e
		DlinkList p = L;
		while (p->next)
			p = p->next;//Point the LinkList p to the end of the bidirectional linked list
		p->next = s;
		s->prior = p;//Insert node * s after p and into L
		s->next = NULL;
		++length;
	} else { // Forward insertion
		s = new DNode; //Generate new node * s
		s->data = e; //Set the node * s data field to e
		s->prior = p->prior; //Insert node * s into L,
		p->prior->next = s;
		s->next = p;
		p->prior = s;
		++length;
	}
	return true;
}

1.6 deletion of double linked list:

Delete the element e inserted before the ith position in the bidirectional linked list L of the leading node. The legal value of i is 1 < = i < = table length.
[analysis]: to delete the p node, you need to solve the problem of the precursor and successor of p!!

• 1. Determine the position i of element e in L, and the pointer p points to the ith position;
• 2. Satisfy: the successor of the precursor of P = = the successor of p;
• 3. Satisfy: subsequent precursors of p = = precursors of p.

p->prior->next = p->next; // Modify the subsequent pointer of the predecessor node of the deleted node
p->next->prior = p->prior; //Modify the precursor pointer of the successor node of the deleted node
delete p; //Free up space for deleted nodes 
--length;

Delete the element e inserted after the ith position in the bidirectional linked list L of the leading node, and the legal value of i is 1 < = i < = table length.
[analysis]: to delete the next node q of p node, we should solve the problem of the precursor and successor pointing of q!!

• 1. Determine the position i of element e in L, and the pointer p points to the ith position;
• 2. Satisfy: the next node of p is the next node of q;
• 3. Satisfaction: q the precursor of the next node is the p node.

// Delete the successor node of p node
bool DeleteNextDNode (DNode *p){
    if (!(p = GetElemP_DuL(L, i))) //Determine the position pointer p of the ith element in L
		return ERROR; 	// When p is NULL, the ith element does not exist
    DNode *q = p->next; // Find the successor node q of p
    if (q==NULL)
        return false;   // p no successor
    p->next=q->next;
    if (q->next!=NULL)  // The q node is not the last node
        q->next->prior=p;
    free(q);    //Free node space
    return true;
}