Hash lookup (hash)

• In the search of linear tables and tree tables, there is no definite relationship between the position of records in the table and the keywords of records. Therefore, a series of keyword comparison is required when searching records in these tables. This kind of search method is based on "comparison", and the efficiency of search depends on the number of comparisons.

Basic concepts of hash table

• Hash function: a function that maps the keyword in the lookup table to the address corresponding to the keyword, which is recorded as hash (key) = addr (the address here can be array subscript, index or memory address).
• Hash functions may map two or more different keywords to the same address, which is called hash collision. These different keywords that collide are called synonyms. On the one hand, a well-designed hash function should minimize such conflicts; On the other hand, because such conflicts are always inevitable, we should design methods to deal with them.
• Hash table: a data structure that is accessed directly based on keywords. That is, the hash table establishes a direct mapping relationship between keywords and storage addresses.
• Ideally, the time complexity of hash table lookup is O(1), which is independent of the number of elements in the table.

Construction method of hash function

• The goal of constructing hash function is to make the hash addresses of all elements evenly distributed on m continuous memory units as much as possible, and make the calculation process as simple as possible to achieve as high time efficiency as possible. According to the structure and distribution of keywords, many different hash functions can be constructed. This paper mainly discusses several common hash function construction methods of integer type keywords.
• When constructing hash functions, you must pay attention to the following points:

1. The definition field of hash function must contain all the keywords to be stored, and the range of value field depends on the size or address range of Hash list
2. The addresses calculated by the hash function should be evenly distributed in the whole address space with equal probability, so as to reduce the occurrence of conflicts.
3. The hash function should be as simple as possible and can calculate the hash address corresponding to any keyword in a short time.

direct addressing

• Directly take the value of a linear function of the keyword as the hash address, and the hash function is
  H ( k e y ) = k e y or H ( k e y ) = a × k e y + b H(key)=key or H(key)=a × key+b H(key)=key or H(key)=a × key+b
  Where a and b are constants. This method is the simplest and will not cause conflict. It is suitable for the situation that the distribution of keywords is basically continuous. If keywords are discontinuous and there are many vacancies, it will cause a waste of storage space.
  

Division method

• This is the simplest, widely applicable and most commonly used method. The division and remainder method uses the remainder obtained by dividing the keyword k by an integer p not greater than the hash table length m as the hash address.
• The hash function h(k) of the division residue method is usually
  h ( k ) = k    m o d    p h(k)= k\;mod\;p h(k)=kmodp(mod is the remainder operation, p ≤ m)
• The key of this method is to select p so that the probability of mapping each keyword in the element set to any address within the hash table after conversion by this function is equal, so as to reduce the possibility of conflict as much as possible. Theoretical research shows that the effect is the best when the prime number is not greater than m.

Digital analysis

• Suppose that the keyword is r-ary number (such as decimal number), and the frequency of R numbers in each bit is not necessarily the same. It may be evenly distributed in some bits, and each number has an equal opportunity to appear; However, some bits are unevenly distributed, and only some numbers often appear. At this time, several bits with more uniform digital distribution should be selected as the hash address. This method is suitable for the known keyword set. If the keyword is replaced, a new hash function needs to be reconstructed.
  

Square middle method

• As the name suggests, this method takes the middle digits of the square value of the keyword as the hash address, and the specific number of digits depends on the actual situation. The hash address obtained by this method is related to each keyword, so the hash address distribution is relatively uniform, and each value of the keyword is not uniform or less than the number of bits required for the hash address.
  

In different cases, different hash functions have different performance, so we can't generally say which hash function is the best. In the actual selection, the method of constructing hash function depends on the keyword set, but the goal is to minimize the possibility of conflict.

Resolution of hash conflict

• It should be noted that any Hash function designed cannot absolutely avoid conflicts. Therefore, we must consider how to deal with the conflict, that is, to find the next "empty" Hash address for the conflicting keyword. use H i H_i Hi indicates the hash address obtained by the i-th detection in the conflict processing, and it is assumed that another hash address is obtained H 1 H_1 H1 ， there was still a conflict, so we had to continue to ask for the next address H 2 H_2 H2, and so on until there is no conflict, then H k H_k Hk ， is the address of the keyword in the table.
• There are many methods to solve hash conflict, mainly including open addressing method and zipper method.

Open addressing

• The so-called open addressing method means that the free address that can store new entries is open to both its synonymous and non synonymous entries. The mathematical recurrence formula is
  H i = ( H ( k e y ) + d i ) H_i=(H(key)+d_i)%m Hi​=(H(key)+di​)
  Where, H ( k e y ) H(key) H(key) is a hash function; i = 0 , 1 , 2 , ... , k ( k ≤ m − 1 ) i=0,1,2,...,k(k≤m-1) i=0,1,2,...,k(k≤m−1)； m m m represents the length of the hash table; d i d_i di is an incremental sequence.
• After a certain increment sequence is selected, the corresponding processing method is determined. There are usually four methods:

1. Linear probing. When d i = 0 , 1 , 2 , , m − 1 d_i=0,1,2,,m-1 When di = 0,1,2,,m − 1, it is called linear detection method. The characteristic of this method is that when a conflict occurs, the next cell in the table is viewed sequentially (when the end address m-1 is detected, the next detection address is the first address 0) until a free cell is found (when the table is not full, a free cell can be found) or the whole table is searched.

• The linear detection method may store the synonyms of the ith hash address in the i + 1st hash address, so the elements that should be stored in the i + 1st hash address compete for the addresses of the elements of the i + 2nd hash address... Thus causing a large number of elements to "gather" (or stack) on the adjacent hash addresses, greatly reducing the search efficiency.

1. Square probing. When d i = 0 ² ， 1 ² ， − 1 ² ， 2 ² ， − 2 ² ， ... k ² ， − k ² d_i=0²，1²，-1²，2²，-2²，...k²，-k² di​=0 ²， one ²， −1 ²， two ²， −2 ²，… k ²， −k ² When, it is called square detection method, where k ≤ m 2 k≤\frac m2 k ≤ 2m, the hash table length m must be a prime number that can be expressed as 4k+3, also known as secondary detection method.

• The square detection method is a better method to deal with conflicts, which can avoid the "stacking" problem. Its disadvantage is that it can not detect all the cells in the hash table, but at least half of the cells can be detected.

1. Hashing method. When d i = H a s h 2 ( k e y ) d_i= Hash_2(key) When di = Hash2 (key), it is called re hashing method, also known as double hashing method. You need to use two hash functions when you pass the first hash function H ( k e y ) H(key) When the address obtained by H(key) conflicts, the second hash function is used H a s h 2 ( k e y ) Hash_2(key) Hash2 (key) calculates the address increment of the keyword. Its specific hash function form is as follows
   H i = ( H ( k e y ) % m + i × h a s h 2 ( k e y ) ) % m H_i=(H(key)\%m+i×hash_2(key))\%m Hi​=(H(key)%m+i×hash2​(key))%m
   Initial detection position H 0 = H ( k e y ) % m H_0=H(key)\%m H0​=H(key)%m. i is the number of conflicts, initially 0. In the re hashing method, after m-11 probes at most, it will traverse all positions in the table and return to H 0 H_0 H0} position.

• Re hashing is not easy to produce aggregation when dealing with conflicts.

1. Pseudo random sequence method. When d i = d_i= When di = pseudo-random number sequence, it is called pseudo-random sequence method.
   ! Note: in the case of open addressing, the existing elements in the table cannot be deleted physically, because if the elements are deleted, the lookup addresses of other elements with the same hash address will be destroyed. Therefore, when you want to delete an element, you can make a deletion mark for it for logical deletion. However, the side effects of this are: after multiple deletions, the hash table looks very full on the surface, but in fact there are many unused positions. Therefore, the hash table needs to be maintained regularly and the elements marked for deletion should be physically deleted.

//Operation algorithm of hash table constructed by open address method
#include <stdio.h>
#define MaxSize 100 / / define the maximum hash table length
#define NULLKEY -1 / / define an empty keyword value
#define DELKEY -2 / / defines the value of the deleted key
typedef int KeyType; //Keyword type
typedef struct
{
	KeyType key; //Keyword domain
	int count; //Detection frequency domain
} HashTable; //Hash table type

void InsertHT(HashTable ha[],int &n,int m,int p,KeyType k) //Insert keyword k into hash table
{
	int i,adr;
	adr=k % p; //Calculate hash function value
	if (ha[adr].key==NULLKEY || ha[adr].key==DELKEY)//k can be placed directly in the hash table
	{
		ha[adr].key=k;
		ha[adr].count=1;
	}
	else //In case of conflict, the linear detection method is used to solve the conflict
	{
		i=1; //i record k the number of conflicts
		do 
		{
			adr=(adr+1) % m; //Linear detection
			i++;
		} while (ha[adr].key!=NULLKEY && ha[adr].key!=DELKEY);
		ha[adr].key=k; //Place k at adr
		ha[adr].count=i; //Set detection times
	}
	n++; //Increase the number of total keywords by 1
}

void CreateHT(HashTable ha[],int &n,int m,int p,KeyType keys[],int n1) //Create hash table
{
	for (int i=0;i<m;i++) //Initial value of setting hash table to null
    {
        ha[i].key=NULLKEY;
	    ha[i].count=0;
    }
	n=0;
	for (i=0;i<n1;i++)
		InsertHT(ha,n,m,p,keys[i]);	//Insert n keywords
}

void SearchHT(HashTable ha[],int m,int p,KeyType k) //Find keyword k in hash table
{
	int i=1,adr;
	adr=k % p; //Calculate hash function value
	while (ha[adr].key!=NULLKEY && ha[adr].key!=k)
	{
		i++; //Cumulative keyword comparison times
		adr=(adr+1) % m; //Linear detection
	}
	if (ha[adr].key==k) //Search succeeded
		printf("Success: Keyword%d，compare%d second\n",k,i);
	else //Search failed
		printf("Failed: Keyword%d，compare%d second\n",k,i);
}

bool DeleteHT(HashTable ha[],int &n,int m,int p,KeyType k) //Delete keyword k in hash table
{
	int adr;
	adr=k % p; //Calculate hash function value
	while (ha[adr].key!=NULLKEY && ha[adr].key!=k)
		adr=(adr+1) % m; //Linear detection
	if (ha[adr].key==k) //Search succeeded
	{
		ha[adr].key=DELKEY; //Delete keyword k
		return true;
	}
	else //Search failed
		return false; //Return false
}

void ASL(HashTable ha[],int n,int m,int p) //Average search length
{
	int i,j;
	int succ=0,unsucc=0,s;
	for (i=0;i<m;i++)
		if (ha[i].key!=NULLKEY)
			succ+=ha[i].count; //Total keyword comparison times when cumulative success
	printf(" In case of success ASL(%d)=%g\n",n,succ*1.0/n);
	for (i=0;i<p;i++)
	{
		s=1; j=i;
		while (ha[j].key!=NULLKEY)
		{
			s++;
			j=(j+1) % m;
		}
		unsucc+=s;
	}
	printf(" In case of failure ASL(%d)=%g\n",n,unsucc*1.0/p);
}

void DispHT(HashTable ha[],int n,int m,int p) //Output hash table
{
	int i,j;
	int succ=0,unsucc=0,s;
	printf("Hashtable :\n");
	printf(" Hash table address:\t");
	for (i=0;i<m;i++) 
		printf(" %3d",i);
	printf(" \n");
    printf(" Hash table key:\t");
	for (i=0;i<m;i++) 
		if (ha[i].key==NULLKEY)
			printf("    ");	 //Output 3 spaces
		else
			printf(" %3d",ha[i].key);
	printf(" \n");
	printf(" Detection times:\t");
	for (i=0;i<m;i++)
		if (ha[i].key==NULLKEY)
			printf("    "); //Output 3 spaces
		else
			printf(" %3d",ha[i].count);
	printf(" \n");
	ASL(ha,n,m,p);
}

int main()
{
	int keys[]={16,74,60,43,54,90,46,31,29,88,77};
	int n,m=13,p=13,k;
	HashTable ha[MaxSize];
	printf("(1)Create hash table\n"); CreateHT(ha,n,m,p,keys,11);
	printf("(2)Show hash table:\n"); DispHT(ha,n,m,p);
	k=29;
	printf("(3)lookup"); SearchHT(ha,m,p,k);
	k=31;
	printf("(4)Deleting: Keywords%d\n",k);
	DeleteHT(ha,n,m,p,k);
	printf("(5)Show hash table:\n"); DispHT(ha,n,m,p);
	printf("(6)lookup"); SearchHT(ha,m,p,k);
	printf("(7)Inserting: Keywords%d\n",k);
	InsertHT(ha,n,m,p,k);
	printf("(8)Show hash table:\n"); DispHT(ha,n,m,p);
	printf("\n");
	return 0;
}

Zipper method

• Obviously, different keywords may be mapped to the same address through the hash function. In order to avoid the conflict of non synonyms, all synonyms can be stored in a linear linked list, which is uniquely identified by its hash address. Suppose that the head pointer of the synonym chain with hash address i is stored in the ith cell of the Hash list, so the search, insert and delete operations are mainly carried out in the synonym chain. Zipper method is suitable for frequent insertion and deletion.
  
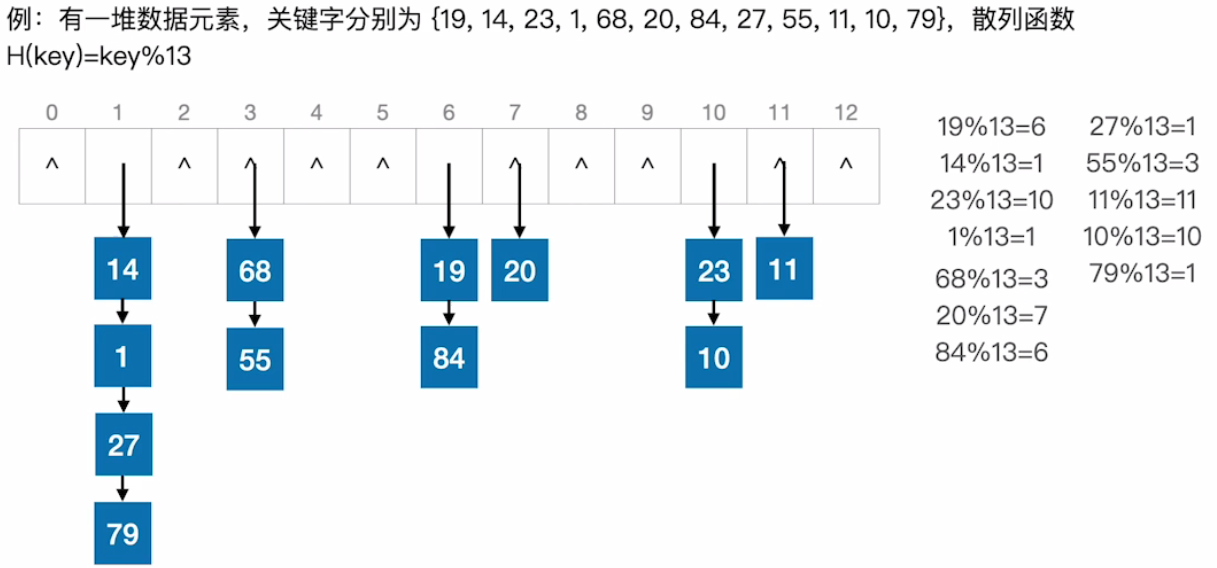
• Compared with the open addressing method, the zipper method has the following advantages:

1. The zipper method is simple to deal with conflicts without accumulation, that is, non synonyms will never conflict, so the average search length is short;
2. Because the node space on each single chain table in the zipper method is dynamically applied, it is more suitable for the situation that the table length cannot be determined before making the table;
3. In order to reduce conflicts, the open addressing method requires that the loading factor A is small, so a lot of space will be wasted when the data scale is large, while a ≥ 1 can be taken in the zipper method, and the pointer field added in the zipper method can be ignored when the elements are large, so space is saved;
4. In the hash table constructed by zipper method, the operation of deleting nodes is easier to implement.

• The zipper method also has disadvantages: the pointer needs additional space, so when the element size is small, the open addressing method saves space. If the saved pointer space is used to expand the size of the hash table, the loading factor can be reduced, which reduces the conflict in the open addressing method and improves the average search speed.

//Operation algorithm of hash table constructed by zipper method
#include <stdio.h>
#include <malloc.h>
#define MaxSize 100 	 // Defines the maximum hash table length
typedef int KeyType; //Keyword type
typedef struct node
{
	KeyType key; //Keyword domain
	struct node *next; //Next node pointer
} NodeType;	 //Single linked list node type
typedef struct
{
	NodeType *firstp; //First node pointer
} HashTable; //Hash table type
void InsertHT(HashTable ha[],int &n,int p,KeyType k) //Insert keyword k into hash table
{
	int adr;
	adr=k % p; //Calculate hash function value
	NodeType *q;
	q=(NodeType *)malloc(sizeof(NodeType));
	q->key=k; //Create a node q to store the keyword k
	q->next=NULL;
	if (ha[adr].firstp==NULL) //If the single linked list adr is empty
		ha[adr].firstp=q;
	else //If the single linked list adr is not empty
	{
		q->next=ha[adr].firstp;	//Insert it into the single linked list of ha[adr] by head interpolation
		ha[adr].firstp=q;
	}
	n++; //The total number of nodes increases by 1
}
void CreateHT(HashTable ha[],int &n,int m,int p,KeyType keys[],int n1) //Create hash table
{
	for (int i=0;i<m;i++) //Hash table initial value
		ha[i].firstp=NULL;
	n=0;
	for (i=0;i<n1;i++)
		InsertHT(ha,n,p,keys[i]); //Insert n keywords
}
void SearchHT(HashTable ha[],int p,KeyType k) //Find keyword k in hash table
{
	int i=0,adr;
	adr=k % p; //Calculate hash function value
	NodeType *q;
	q=ha[adr].firstp; //q points to the first node of the corresponding single linked list
	while (q!=NULL)	 //Scan all nodes of single linked list adr
	{
		i++;
		if (q->key==k) //Search succeeded
			break; //Exit loop
		q=q->next;
	}
	if (q!=NULL) //Search succeeded
		printf("Success: Keyword%d，compare%d second\n",k,i);
	else //Search failed
		printf("Failed: Keyword%d，compare%d second\n",k,i);
}

bool DeleteHT(HashTable ha[],int &n,int m,int p,KeyType k) //Delete keyword k in hash table
{
	int adr;
	adr=k % p; //Calculate hash function value
	NodeType *q,*preq;
	q=ha[adr].firstp; //q points to the first node of the corresponding single linked list
	if (q==NULL) 
		return false; //The corresponding single linked list is empty
	if (q->key==k) //The first node is k
	{
		ha[adr].firstp=q->next; //Delete node q
		free(q);
		n--; //Total number of nodes minus 1
		return true; //Return true
	}
	preq=q; q=q->next; //When the first node is not k
	while (q!=NULL)
	{
		if (q->key==k) //Search succeeded
			break; //Exit loop
		q=q->next;
	}
	if (q!=NULL) //Search succeeded
	{
		preq->next=q->next; //Delete node q
		free(q);
		n--; //Total number of nodes minus 1
		return true; //Return true
	}
	else return false; //k not found, return false
}

void ASL(HashTable ha[],int n,int m) //Average search length
{
	int succ=0,unsucc=0,s;
	NodeType *q;
	for (int i=0;i<m;i++) //Scan all hash table address spaces
	{
		s=0;
		q=ha[i].firstp; //q points to the first node of the single linked list i
		while (q!=NULL) //Scan all nodes of single linked list i
		{
			q=q->next;
			s++; //s records the number of nodes in the corresponding single linked list
			succ+=s; //Cumulative total number of successful comparisons
		}
		unsucc+=s; //Total number of cumulative unsuccessful comparisons
	}
	printf(" In case of success ASL(%d)=%g\n",n,succ*1.0/n);
	printf(" In case of failure ASL(%d)=%g\n",n,unsucc*1.0/m);
}

void DispHT(HashTable ha[],int n,int m) //Output hash table
{
	int succ=0,unsucc=0,s;
	NodeType *q;
	for (int i=0;i<m;i++) //Scan all hash table address spaces
	{
		s=0;
		printf(" %3d:\t",i);
		q=ha[i].firstp; //q points to the first node of the single linked list i
		while (q!=NULL) //Scan all nodes of single linked list i
		{
			printf("%4d",q->key);
			q=q->next;
			s++; //s records the number of nodes in the corresponding single linked list
			succ+=s; //Cumulative total number of successful comparisons
		}
		unsucc+=s; //Total number of cumulative unsuccessful comparisons
		printf("\n");
	}
	printf(" In case of success ASL(%d)=%g\n",n,succ*1.0/n);
	printf(" In case of failure ASL(%d)=%g\n",n,unsucc*1.0/m);
}

void DestroyHT(HashTable ha[],int m) //Destroy hash table
{
	int i;
	NodeType *q,*preq;
	for (i=0;i<m;i++)
	{
		q=ha[i].firstp; //q points to the first node of the single linked list i
		while (q!=NULL) //Scan all nodes of single linked list i
		{
			preq=q; q=q->next;
			free(preq);
		}
	}
}

int main()
{
	int keys[]={16,74,60,43,54,90,46,31,29,88,77};
	int n,m=13,p=13,k=29;
	HashTable ha[MaxSize];
	printf("(1)Create hash table\n"); CreateHT(ha,n,m,p,keys,11);
	printf("(2)Show hash table:\n"); DispHT(ha,n,m);
	printf("(3)lookup"); SearchHT(ha,p,k);
	k=77;
	printf("(4)Deleting: Keywords%d\n",k);
	DeleteHT(ha,n,m,p,k);
	printf("(5)Show hash table:\n"); DispHT(ha,n,m);
	printf("(6)lookup"); SearchHT(ha,p,k);
	printf("(7)Inserting: Keywords%d\n",k);
	InsertHT(ha,n,p,k);
	printf("(8)Show hash table:\n"); DispHT(ha,n,m);
	printf("\n");
	DestroyHT(ha, m); //Destroy hash table
	return 0;
}

Hash lookup and performance analysis

• The search process of hash table is basically the same as that of constructing Hash list. For a given keyword key, the hash address can be calculated according to the hash function. The steps are as follows:
  Initialization: addr=Hash(key);
  ① Check whether there is a record at the location with address Addr in the lookup table. If there is no record, the query failure is returned; If there is a record, compare it with the value of key. If it is equal, return the search success flag. Otherwise, execute step ②
  ② Calculate the "next hash address" with the given conflict handling method, set Addr as this address, and go to step ①
  

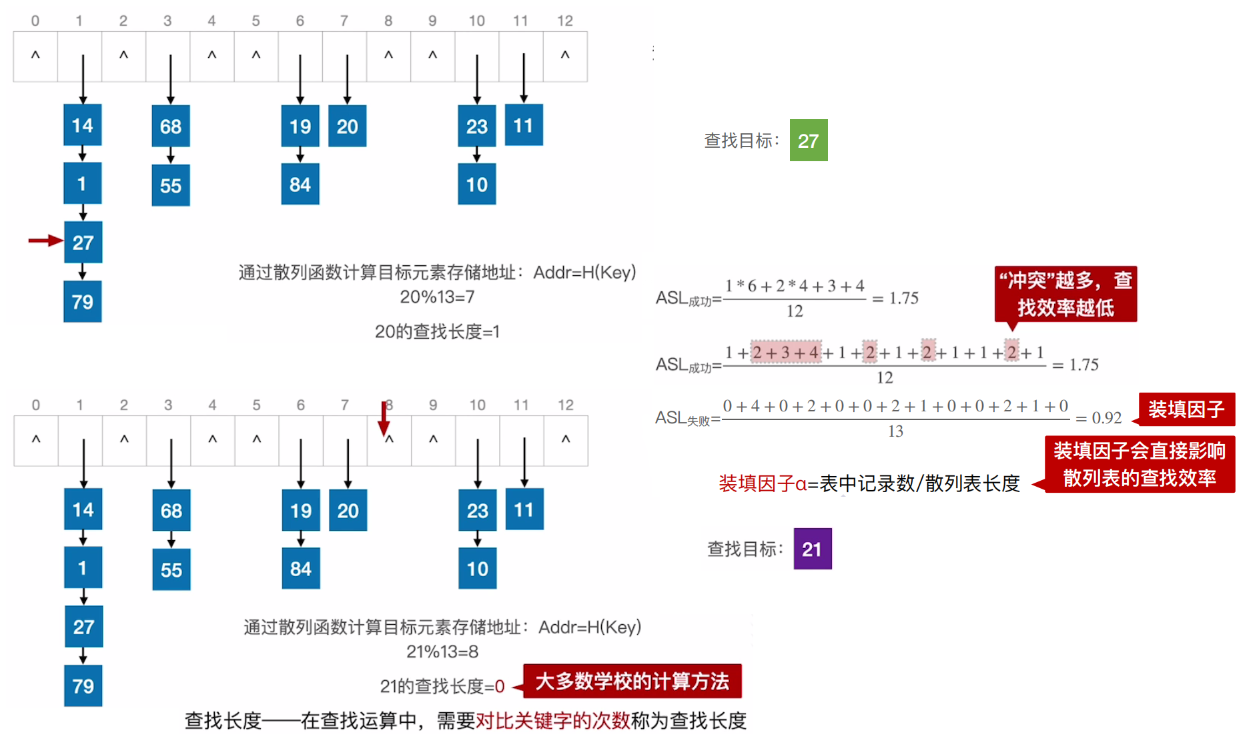
In the hash table, although conflicts are difficult to avoid, the possibility of conflicts is different, which will affect the performance of hash lookup. Hash search performance is mainly related to three factors:

1. It is related to filling factor a. The so-called load factor refers to the ratio of the number of elements n stored in the hash table to the size m of the hash address space, i.e a = n m a=\frac nm a=mn​. A the smaller the, the less likely the conflict is; A the greater (maximum 1) the greater the likelihood of conflict. This is easy to understand, because the smaller a, the larger the proportion of free cells in the hash table, so the less likely there is a conflict between the elements to be inserted and the elements already inserted; On the contrary, the larger a, the smaller the proportion of free cells in the hash table, so the greater the possibility of conflict between the elements to be inserted and the elements already inserted. On the other hand, the smaller a, the lower the utilization of storage space; Conversely, the higher the utilization of storage space. In order to reduce conflicts and improve the utilization of storage space, the final a is usually controlled in the range of 0.6 ~ 0.9.
2. Related to the hash function used. If the hash function is properly selected, the hash address can be evenly distributed in the hash address space as much as possible, so as to reduce the occurrence of conflict; Otherwise, if the hash function is not selected properly, the hash address may be concentrated in some areas, thus increasing the occurrence of conflicts.
3. When a hash conflict occurs, a method to solve the hash conflict needs to be taken, so the hash lookup performance is also related to the method to solve the conflict.

• For pre-known and small-scale keyword sets, we can usually find hash functions that do not conflict, so as to avoid conflicts, make the search time complexity O(1), and improve the search efficiency. Therefore, we should try our best to design a perfect hash function for keyword sets that are searched frequently.