Data structure*

Single linked list, C reverse order and C two increasing linked lists are combined into one increasing linked list

Job address
MOOC
Please complete the following algorithm to fill in the blank to realize the reverse storage of the sequence table. The reverse storage refers to the sequential storage after reversing the linear relationship of elements, such as (a0,a1,a2), and the reverse of the relationship is (a2,a1,a0)
The structure of SeqList is defined as follows:

typedef struct seqList
{
    int n;
    int maxLength;
    ElemType *element;
}SeqList;

void Invert(SeqList *L) {
ElemType temp; int i; 
for ( i=0; i<________; i++) { 
    temp =____________; 
    L->element[i] = L->element[___________]; 
    L->element[________] = ___________; }
}

Reference answer:

`void Invert(SeqList *L)
{
    ElemType temp;
    int i;
    for(i = 0;i<n/2;i++)        //The actual length of the current array is n, so n/2 cycles are enough
    {
        temp = L->element[i];
        L->element[i] = L->element[n-1-i];
        L->element[n-1-i] = temp;
        
    }
}`

This is a basic introductory question. Maybe the circular condition of for() function is not easy to get along with, but the internal statement block of for should be easy to take notes to solve. If it is not clear, it is recommended to watch the data structure by Mr. Hao bin. The link is as follows (the reason why it was not given at the beginning is for everyone to think about it again): BiliBIli

Please complete the following algorithm to fill in the blank to realize the inverted storage of single chain table. The inverted storage refers to the storage of chain table after reversing the linear relationship of elements, such as (a0,a1,a2), and the inverted relationship is (a2,a1,a0)
Single chain table Node and single chain table SingleList structure are defined as follows:

typedef struct node
{
     ElemType element;
     struct node *link;
}Node;

typedef struct singlelist
{
    Node *first;
    int n;
}SingleList;

void invert(SingleList *L) { 
Node *p=__________,*q; 
L->first=NULL; 
while (_____) { 
    q=p->link; 
    p->link=_______; 
    L->first=_______; 
    p=_______; } 
}

Reference answer

void invert(SingleList *L)
{
    Node *p = L->first ,*q;     //Make p point to the first node
    L->first = NULL;
    while(p != NULL)            //Judge whether p points to the tail node
    {
        q = p->link;        //q points to the next node of p
        p->link = L->first ;
        L->first = p;
        p = q;
    }
}

This problem is to use two new pointers to change the node point from the back to the beginning. The final result is that l - > first points to the tail node, p = q = NULL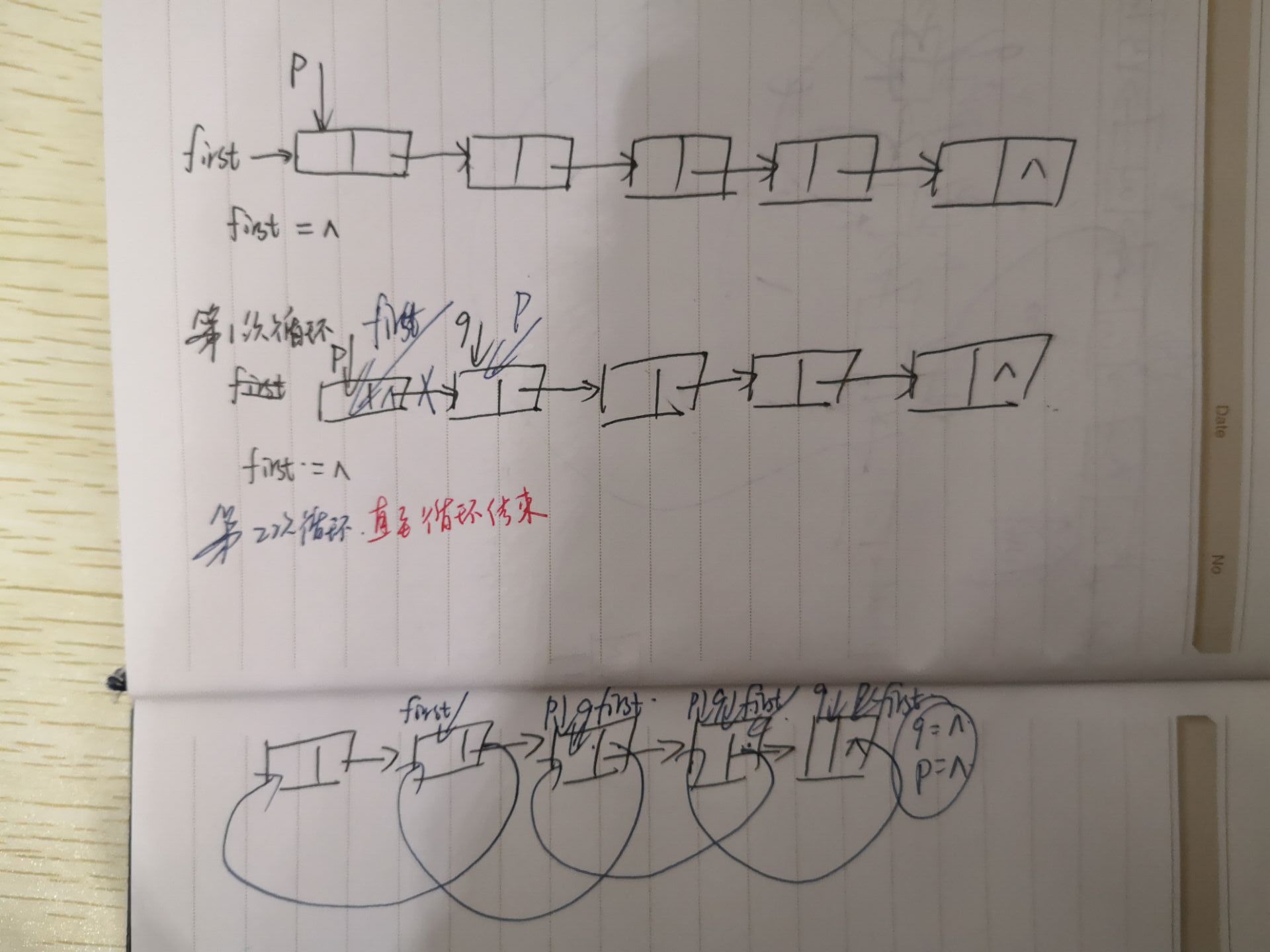

Complete the following algorithm to fill in the blank, and merge the two ordered increasing single chain tables with header nodes into one ordered increasing single chain table.
The Node of the list Node and the SingleList structure are defined as follows:

typedef struct node
{
     ElemType element;
     struct node *link;
}Node;

typedef struct headerlist
{
    Node *head;
    int n;
}HeaderList;

void MergeList1(HeaderList *La,HeaderList *Lb,HeaderList *Lc) { 
//Merge the linked list La and Lb. the new merged table points to the 
Node *pa,*pb,*pc,*q;
pa=La->head->link; 
pb=Lb->head->link; 
pc=Lc->head; 
while(pa && pb) {
     if(____________________) { 
           pc->link=pa; 
           pc=pa; 
           pa=pa->link; 
           La->n--; }
     else if(pa->element>pb->element) { 
           pc->link=___________; 
           pc=________; 
           pb=_________;
           Lb->n--; } 
      else { 
           pc->link=pa; 
           pc=pa; 
           pa=_________; 
           q=_________; 
           free(pb); 
           pb =q; } 
Lc->n++; } 
pc->link=pa?pa:pb; //Insert the remaining segment LC - > N + = Pa? La - > n: LB - > n; 
}

Reference answer:

while(pa&&pb)           //Judge who gets to the end of the linked list first
{                           /*There are three cases. Look at the value of the node that pa and pb currently point to*/
    if(pa->element < pb->element)           /*When the value in the node that pa points to is less than the value in the node that Pb points to*/
    {
        pc->link = pa;                          //Pointer in Lc list the pointer domain of pc points to the node pa points to
        pc = pa;                             //The pointer pc in Lc list points to the node position of pa to prepare for the next cycle
        pa = pa->link;                          //pa moves to the next node of La list
        La->n--;                                //La's list length minus one
    }
    else if(pa->element > pb->element)       /*When the value of pa in the node is greater than that of Pb in the node*/
    {
        pc->link = pb;                           //Pointer in Lc list the pointer domain of pc points to the node that pb points to
        pc = pb;                       //The pointer pc in Lc list points to the node position pointed by pa, which is ready for the next cycle
        pb = pb->link;              //pb moves to the next node of the Lb list
        Lb->n--;                        //Length of link list of Lb minus one
    }
    else                     /*When the value in the node that pa points to = the value in the node that pb points to*/
    {
        pc->link = pa;           //Pointer in Lc list the pointer domain of pc points to the node pa points to
        pc = pa;                 //The pointer pc in Lc list points to the node position of pa to prepare for the next cycle
        pa = pa->link;      //pa moves to the next node of La list
        q = pb->link;           //Define a new pointer to store pb in the next node of Lb
        free(pb);               //Release the dynamic memory of current pb
        pb = q;
    }
    Lc->n++;                Before the end of each cycle Lc Length of plus one
}

This question is annotated in detail. I'm just starting to learn, and I have limited expression of professional terms on data structure. So I would be very happy if I could give you any help. If there is any problem or improvement, please send me a private message. Thank you!