Basic concepts
- A linear table is a finite sequence of n data elements. The elements in the same linear table must have similarity
- Do not care about the specific data between elements, but about the relationship between elements
- Linear table operations: create, judge whether it is empty, determine the length, find, delete and insert
Array description (sequential storage)
- C + + class definition
template<class T>
class LinearList{
public:
LinearList(int MaxListSize=10); //Constructor
~LinearList(){delete[] element;) //Destructor
bool IsEmpty() const{return length==0;}
int Length() const(return length;)
bool Find(int k,T& x) const; //Reference to return the k-th element of the list
int Search(const T& x) const; //Returns the position of x (no duplicate elements)
LinearList<T> Delete(int k,T& x); //Delete the k-th element and save it in x
LinearList<T>& Insert(int k, const T& x); //Insert x after the k th element
void Output(ostream& out) const;
private:
int length;
int MaxSize; //Fixed part, ignore
T *element; //One dimensional dynamic array
}
- C + + implementation: create and release
template<class T>
LinearList<T>::LinearList(int MaxListSize){
MaxSize=MaxListSize;
element=new T[MaxSize]; //Time complexity: constant level
length=0;
}
~Linearlist(){ //Time complexity: constant level
delete[] element;
}
- lookup
template<class T>
bool LinearList<T>::Find(int k,T& x) const{
if(k<1||k>length)
return false;
x=element[k-1];
return true;
} //Time complexity: O(1)
template<class T>
bool LinearList<T>::Search(int k,T& x) const{
for(int i=0;i<length;i++)
if(element[i]==x)
return ++i;
return 0;
} //Time complexity: O(length)
- delete
template<class T>
LinearList<T>& LinearList<T>::Delete(int k,T& x){
if(Find(k,x)){ //If the element can be found
for(int i=k;i<length;i++)
element[i-1]=element[i]; //Move the following elements forward one space
length--;
return *this;
} //Time complexity: O(length-k)
else
throw OutOfBounds(); //Out of bounds, exception
return *this;
}
template<class T>
LinearList<T>& LinearList<T>::Insert(int k,const T& x){
if(k<0||k>length)
throw OutOfBounds(); //k illegal
if(length==MaxSize)
throw NoMem(); //Table space is full and cannot be inserted again
for(int i=length-1;i>=k;i--) //General situation
element[i+1]=element[i];
element[k]=x;
length++;
return *this;
//Problem: the element needs to be moved, and it is easy to overflow
} //Time complexity: O(length-k)
- output
template<class T>
void LinearList<T>::Output(ostream& out) const{
for (int i=0;i<length;i++)
out<<element[i]<<" ";
}
//heavy load
template<class T>
ostream& operator<<(ostream& out, const LinearList<T>& x){
x.Output(out);
return out;
}
- Evaluation: low space efficiency
Linked list description
- Linked list node: ChainNode
template<class T>
class ChainNode{
friend Chain<T>; //Declared friend class
friend ChainIterator<T>;
private:
T data; //Stored data
ChainNode<T> *link; //Point to next node
}
- Unidirectional linked list
template<class T>
class Chain{
friend ChainIterator<T>;
public:
Chain(){first=0;} //Create an empty linked list
~Chain();
bool IsEnmpty()const {return first==0;}
int Length() const;
bool Find(int k,T& x) const;
int Search(const T& x) const;
Chain<T>& Delete(int k,T& x);
Chain<T>& Insert(int k,const T& x);
void Output(ostream& out) const;
private:
ChainNode<T> *first; //First pointer
}
template<class T>
Chain<T>::~Chain(){
ChainNode<T> *next; //A temporary variable that controls the pointer
while(first){ //The next node exists
next=first->link;
delete first;
first=next;
}
} //Time complexity: O(n)
template<class T>
int Chain<T>::Length()const{
ChainNode<T> *current=first;
int len=0;
while(current){
len++;
current=current->link;
}
return len;
} //Time complexity: O(n)
template<class T>
bool Chain<T>::Find(int k, T& x) const{
if(k<1)
return false;
ChainNode<T> *current=first;
int index=1;
while(index<k&¤t){
current=current->link;
index++;
}
if(current){ //If the pointer points to something real
x=current->data;
return true;
}
return false;
} //Time complexity: O(k)
template<class T>
bool Chain<T>::Search(const T& x) const{
ChainNode<T> *current=first;
int index=1; //Used to record where x is
while(current&¤t->data!=x){ //If you haven't found x
current=current->link;
index++;
}
if(current) //If the pointer points to something real
return index;
return 0;
} //Time complexity: O(n)
template<class T>
void Chain<T>::Output(ostream& out)const{
ChainNode<T> *current;
for (current=first;current;current=current->link)
out << current->data << " ";
}
//Operator overloading
template <class T>
ostream& operator<<(ostream& out, const Chain<T>& x){
x.Output(out);
return out;
} //Time complexity: O(n)
template<class T>
Chain<T>&Chain<T>::Delete(int k, T& x){
if(k<1||first) //If k is illegal or the linked list is empty
throw OutOfBounds();
ChainNode<T> *p=first; //A temporary variable that eventually points to the k-th element
if(k==1) //If you want to delete the first element
first=first->link; //Update linked list header element
else{ //If you want to delete the middle element
ChainNode<T> *q=first; //You want it to point to the previous element of the element you want to delete
for(int index=1;index<k-1&&q;index++)
q=q->link; //Pointer shift right
if(!q||!q->link) //k> Linked list length
throw OutOfBounds();
p=q->link;
q->link=p->link;
}
x=p->data;
delete p; //Release the memory space occupied by item k, but do not delete the data. It may be used elsewhere
return *this;
} //Time complexity: O(n)
template<class T>
Chain<T>&Chain<T>::Insert(int k, const T& x){
if(k<0) //If k is illegal
throw OutOfBounds();
ChainNode<T> *p=first; //A temporary variable that eventually points to the k-th element
for(int index=1;index<k&&p;index++)
p=p->link;
if(k>0&&!p)
throw OutOfBounds();//k> Linked list length
ChainNode<T> *y=new ChainNode<T>;
y->data=x; //Add a new node
if(k){
y->link=p->link;
p->link=y; //Insert operation
}
else{ //When k=0, the chain header element is inserted
y->link=first;
first=y; //Remember to update the header node
}
return *this;
}
template<class T>
void Chain<T>::Erase(){ //Delete all nodes of the linked list
ChainNode<T> *next;
while (first){
next = first->link;
delete first;
first = next;
}
}
template<class T>
Chain<T>& Chain<T>::Append(const T& x){ //Add an element at the end of the linked list
ChainNode<T> *y;
y = new ChainNode<T>;
y->data = x;
y->link = NULL;
if (first) {//If the linked list is not empty
last->link = y;
last = y;
}
else //The linked list is empty
first = last = y;
return *this;
}
- Two improved forms
(1) Point the tail node to the head node
(2) Add a header node that does not store data template<class T>
bool Chain<T>::Search(const T& x) const{ //Optimization of Search function of leading node
ChainNode<T> *current=first->link;
int index=1; //Used to record where x is
first->data=x; //Save the value of x in an empty header node and set an termination condition
while(current->data!=x){ //If you haven't found x
current=current->link;
index++;
}
return ((current==first)?0:index); //If it points to the head node, it means that it is not found in the linked list
}
- Bidirectional linked list
template <class T>
class DoubleNode {
friend Double<T>;
private:
T data;
DoubleNode<T> *left, *right;
};
template<class T>
class Double {
public:
Double() {LeftEnd = RightEnd = 0;};
~Double();
int Length() const;
bool Find(int k, T& x) const;
int Search(const T& x) const;
Double<T>& Delete(int k, T& x);
Double<T>& Insert(int k, const T& x);
void Output(ostream& out) const;
private:
DoubleNode<T> *LeftEnd, *RightEnd; //* RightEnd can be omitted from the two-way circular linked list
};
- summary
(1) Spatial complexity
The formulaic space is all used to save the list data, while the linked list has additional space to save the link pointer
The linked list is dynamically allocated, the occupied space is proportional to the current linked list size, and the utilization rate is high; The formulation is static distribution, which can not predict the actual demand, resulting in waste or shortage
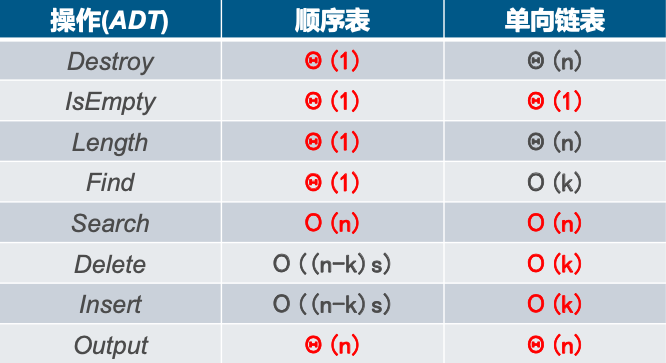
(2) Time complexity
The performance of inserting and deleting operations is better described by linked list, while the performance of random access is better described by formula
Application of linear table
bin sort
- A lot of data is stored
- Limited range of stored data
- Sorting method realized by linked list
Delete each node (head node) of the linked list one by one
Put the deleted node into the appropriate box (insert the head position of the corresponding linked list)
Collect and link all boxes to generate a sorting linked list (adjacent boxes are connected from beginning to end) class Node {
friend ostream& operator<<(ostream&, const Node &);
friend void BinSort(Chain<Node>&, int);
public:
int operator !=(Node x) const{ //Operator overloading
return (score != x.score);
}
private:
int score;
char *name;
};
ostream& operator<<(ostream& out, const Node& x) { //Operator overloading
out << x.score << ' ';
return out;
}
void BinSort(Chain<Node>& X,int range){ //Value range of element
int len=X.length();
Node x;
Chain<Node> *bin;
bin=new Chain<Node>[range+1];
for(int i=1;i<len;i++){
X.Delete(1,x); //Delete header node
bin[x.score].Insert(0,x); //Insert into the head of the new linked list
} //O(n)
for(int j=range;j>=0;j--) //Starting from the last box, insert the large data into the ordered linked list first, because each insertion is at the head, so the large elements will go to the back
while(!bin[j].IsEmpty()){ //If the box is not empty (it is already empty or has been taken)
bin[j].Delete(1,x); //Delete header node
X.Insert(0,x); //Insert into the head of the ordered linked list
} //O(n+range)
delete[] bin;
} //Time complexity: 2n+range
//Problem: there are many times of new and Delete in Delete and Insert, and this is required for each cycle
//update: avoid frequent calls to Delete and Insert
template<class T>
void Chain<T>::BinSort(int range){ //Sort the box as a member function of the linked list
int b;
ChainNode<T> **bottom, **top; //Initialize box
bottom=new ChainNode<T>* [range+1];
top=new ChainNode<T>* [range+1];
for(b=0;b<=range;b++)
bottom[b]=NULL;
for(;first;first=first->link){
b=first->data;
if(bottom[b]){ //If the box is not empty
top[b]->link=first;
top[b]=first;
}
else
bottom[b]=top[b]=first;
}
ChainNode<T> *y=0;
for(b=0;b<=range;b++)
if(bottom[b]){
if(y)
y->link=bottom[b];
else
first=bottom[b];
y=top[b];
}
if(y)
y->link=0;
delete[] bottom;
delete[] top;
} //Time complexity: n+2range
Cardinality sort
Assignment 2
Splice the two linked lists alternately into a linked list
//Splice the two linked lists alternately into a linked list
template <typename T>
class extendedChain{
struct node{
T data;
node *next;
};
public:
node *head; //Head node
extendedChain(); //Constructor
void append(T t); //Splice the data at the end of the linked list
void display(); //Output linked list
bool empty(); //Determine whether the linked list is empty
void deleteHead(); //Delete header element
};
template <typename T>
extendedChain<T>::extendedChain(){
head=NULL;
}
template <typename T>
void extendedChain<T>::append(T t){
node *p=new node;
p->data=t;
p->next=NULL;
if(head==NULL){ //If the linked list has not been created
head=p;
return;
}
node *tail=head;
while(tail->next) //Find the location of the tail node
tail=tail->next;
tail->next=p; //Connect the new node to the back
}
template <typename T>
void extendedChain<T>::display(){
node *p=head;
while(p){ //Sequential output
cout<<p->data<<" ";
p=p->next;
}
cout<<endl;
}
template <typename T>
bool extendedChain<T>::empty(){
if(head)
return false;
else
return true;
}
template <typename T>
void extendedChain<T>::deleteHead(){
node *p=head;
head=p->next; //Update header node
}
template <typename T>
void meld(extendedChain<T> a,extendedChain<T> b){
extendedChain<T> c;
while(!a.empty()&&!b.empty()){ //When neither is empty
c.append(a.head->data);
c.append(b.head->data);
a.deleteHead();
b.deleteHead();
}
while(!b.empty()){ //Add all the remaining elements to c
c.append(b.head->data);
b.deleteHead();
}
while(!a.empty()){
c.append(a.head->data);
a.deleteHead();
}
c.display();
}
int main(){
extendedChain<int> a,b;
cout<<"Please input 7 integers in entended chain a!"<<endl;
int t;
for(int i=1;i<=7;i++){
cin>>t;
a.append(t);
}
cout<<"Please input 10 integers in entended chain b!"<<endl;
for(int i=1;i<=10;i++){
cin>>t;
b.append(t);
}
meld(a, b);
return 0;
}
Split a linked list into two linked lists according to the index
//Split a linked list into two lists according to the index
template <typename T>
class extendedChain{
struct node{
T data;
node *pre; //Bidirectional cycle
node *next;
};
public:
node *head;
node *mark;
extendedChain();
void append(T t);
void display();
bool empty();
void deleteHead();
void split();
};
template <typename T>
extendedChain<T>::extendedChain(){
head=NULL;
}
template <typename T>
void extendedChain<T>::append(T t){
node *p=new node;
p->data=t;
p->next=NULL;
if(head==NULL){
head=p;
return;
}
node *tail=head;
while(tail->next)
tail=tail->next;
tail->next=p;
p->pre=tail;
}
template <typename T>
void extendedChain<T>::display(){
node *p=head;
while(p){
cout<<p->data<<" ";
p=p->next;
}
cout<<endl;
}
template <typename T>
bool extendedChain<T>::empty(){
if(head)
return false;
else
return true;
}
template <typename T>
void extendedChain<T>::deleteHead(){
node *p=head;
head=p->next;
p->pre=NULL;
}
template <typename T>
void extendedChain<T>::split(){
}
void split(extendedChain<int>c){ //Non member function method
extendedChain<int>a,b;
c.mark=c.head;
int index=1;
while(c.mark){
if(index%2==0) //Index is double
b.append(c.mark->data);
else //Index is single
a.append(c.mark->data);
c.mark=c.mark->next;
index++;
}
a.display();
b.display();
}
int main(){
extendedChain<int> c;
cout<<"Please input 10 integers in entended chain c!"<<endl;
int t;
for(int i=1;i<=10;i++){
cin>>t;
c.append(t);
}
split(c);
return 0;
}
