1, The concept of red black tree
- Red Black tree is a binary search tree, but a storage bit is added on each node to represent the color of the node, which can be red or Black. By limiting the coloring mode of each node on any path from root to leaf, the red Black tree ensures that its longest path does not exceed twice the shortest path, so it is close to balance.
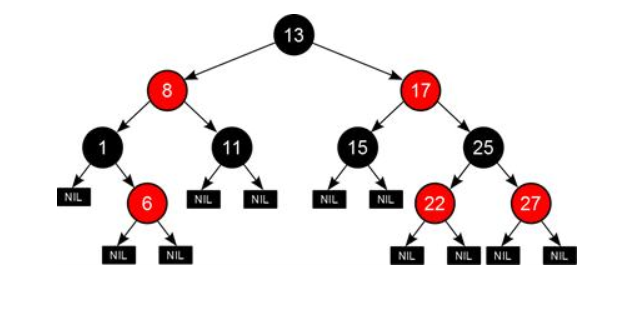
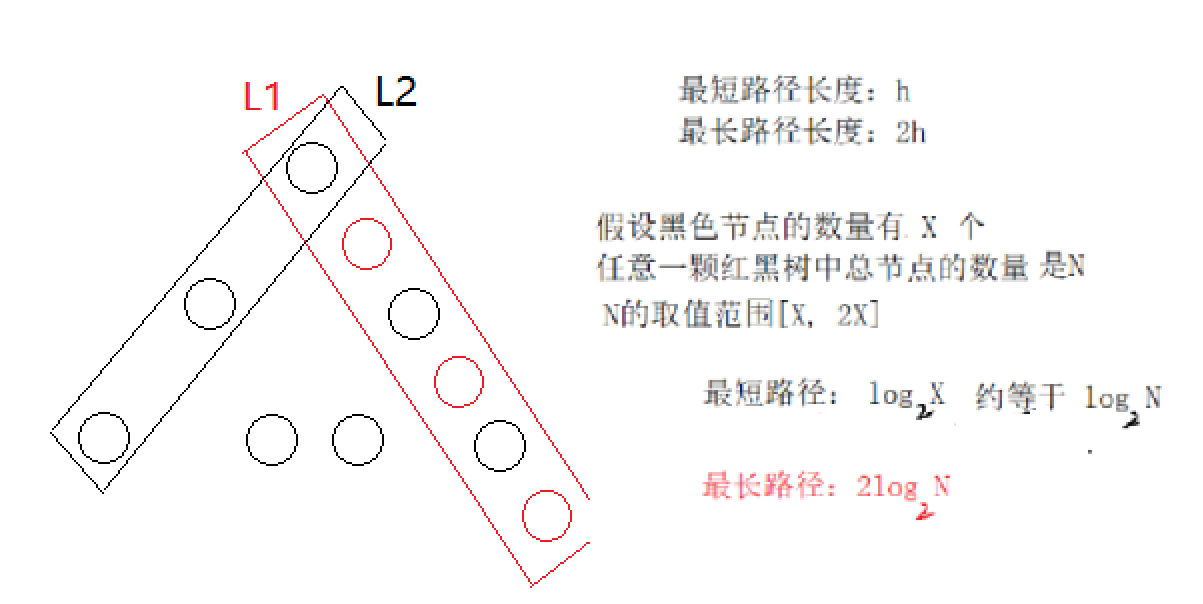
On the longest path and shortest path problem: suppose a red black tree has h black nodes on each path.
2, The nature, definition and structure of red black tree
(1) Nature
- Each node is either red or black.
- The root node is black.
- There are no two consecutive red nodes.
- Each path has the same black node.
- Each leaf node is black (here leaf node refers to the empty node NIL).
(2) Definition
// The color of the node
enum Color{RED, BLACK};
// Definition of red black tree node
template<class ValueType>
struct RBTreeNode
{
RBTreeNode(const ValueType& data = ValueType(),Color color = RED)
: _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr)
, _data(data), _color(color)
{}
RBTreeNode<ValueType>* _pLeft; // Left child of node
RBTreeNode<ValueType>* _pRight; // Right child of node
RBTreeNode<ValueType>* _pParent; // Parent of the node (the red black tree needs to be rotated, and this field is given for simplicity)
ValueType _data; // Value range of node
Color _color; // The color of the node
};
Here, we find that the default color of nodes is red, because the nature of inserting red node tree may not change, while inserting black nodes will violate property 4 every time Setting the node to red has little impact on the red black tree when inserting, while black is the largest. Therefore, in order to minimize the impact, the default node color is red.
(3) Structure
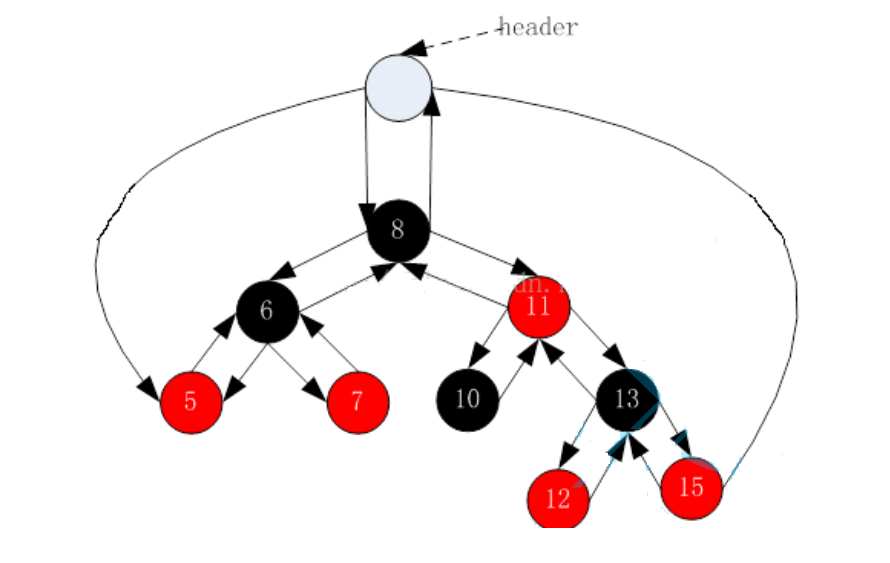
- In order to simplify the subsequent implementation of the associated container, a head node is added in the implementation of the red black tree, because the heel node must be black. In order to distinguish from the root node, the head node is black, and the parent field of the head node points to the root node of the red black tree, and the left field points to the smallest node in the red black tree_ The piright domain points to the largest node in the red black tree, as follows:
3, Insertion and verification of red black tree
(1) Insert
The red black tree is based on the binary search tree with its balance constraints. Therefore, the insertion of red black tree can be divided into two steps:
1. Insert a new node according to the tree rules of binary search
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return make_pair(_root, true);
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(cur, false);
}
}
cur = new Node(kv); // RED
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
2. Check whether the nature of the red black tree is damaged after the new node is inserted
Because the default color of the new node is red, if the color of its parent node is black and does not violate any property of the red black tree, it does not need to be adjusted; However, when the color of the parent node of the newly inserted node is red, it violates property 3 and cannot have connected red nodes. At this time, it is necessary to discuss the red black tree according to the situation:
Convention: cur is the current node, p is the parent node, g is the grandfather node, and u is the uncle node
Case 1: cur is red, p is red, g is black, and u exists and is red
Case 2: cur is red, p is red, g is black, u does not exist / u is black
Case 3: cur is red, p is red, g is black, u does not exist / u is black
pair<Node*, bool> Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return make_pair(_root, true);
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(cur, false);
}
}
cur = new Node(kv); // RED
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
Node* newnode = cur;
//
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (grandfather->_left == parent)
{
Node* uncle = grandfather->_right;
// Case 1: u exists and is red
if (uncle && uncle->_col == RED)
{
// Discoloration
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
// Continue to process upward
cur = grandfather;
parent = cur->_parent;
}
else // Case 2 + 3: u does not exist or exists and is black
{
// g
// p
// c
//
if (cur == parent->_left) //
{
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
// g
// p
// c
//
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else // grandfather->_right == parent
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else // Case 2 + 3: u does not exist or exists and is black
{
if (cur == parent->_right)
{
RotateL(grandfather);
grandfather->_col = RED;
parent->_col = BLACK;
}
else
{
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return make_pair(newnode, true);
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* parentParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)
{
parentParent->_left = subL;
}
else
{
parentParent->_right = subL;
}
subL->_parent = parentParent;
};
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
subR->_left = parent;
Node* parentParent = parent->_parent;
parent->_parent = subR;
if (_root == parent)
{
_root = subR;
}
else
{
if (parentParent->_left == parent)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
}
subR->_parent = parentParent;
}1. Random insertion to construct red black tree
2. Insert and construct red black tree in descending order
3. Insert and construct the red black tree in ascending order
(2) Verify
The detection of red black tree is divided into two steps:
1. Check whether it meets the binary search tree (whether the middle order traversal is an ordered sequence)
2. Check whether it meets the properties of red black tree
bool IsValidRBTree()
{
PNode pRoot = GetRoot();
// Empty trees are also red and black trees
if (nullptr == pRoot)
return true;
// Check whether the root node meets the requirements
if (BLACK != pRoot->_color)
{
cout << "Violation of red black tree property 2: the root node must be black" << endl;
return false;
}
// Gets the number of black nodes in any path
size_t blackCount = 0;
PNode pCur = pRoot;
while (pCur)
{
if (BLACK == pCur->_color)
blackCount++;
pCur = pCur->_pLeft;
}
// Check whether the property of red black tree is satisfied. k is used to record the number of black nodes in the path
size_t k = 0;
return _IsValidRBTree(pRoot, k, blackCount);
}
bool _IsValidRBTree(PNode pRoot, size_t k, const size_t blackCount)
{
//After going to null, judge whether k and black are equal
if (nullptr == pRoot)
{
if (k != blackCount)
{
cout << "Violation nature 4: the number of black nodes in each path must be the same" << endl;
return false;
}
return true;
}
// Count the number of black nodes
if (BLACK == pRoot->_color)
k++;
// Check whether the current node and its parents are red
PNode pParent = pRoot->_pParent;
if (pParent && RED == pParent->_color && RED == pRoot->_color)
{
cout << "Violation nature 3: no connected red nodes" << endl;
return false;
}
return _IsValidRBTree(pRoot->_pLeft, k, blackCount) &&
_IsValidRBTree(pRoot->_pRight, k, blackCount);
}
4, Application of red black tree
1. C++ STL library -- map/set, until_ map/mutil_ set
2. Java library
3. linux kernel
4. Other libraries
5, Comparison between red black tree and AVL tree
- Both red black trees and AVL trees are efficient balanced binary trees. The time complexity of adding, deleting, modifying and checking is O(). Red black trees do not pursue absolute balance. They only need to ensure that the longest path does not exceed twice the shortest path. Relatively speaking, the number of insertion and rotation is reduced. Therefore, in the structure of frequent addition and deletion, neutral energy is better than AVL trees, and the implementation of red black trees is relatively simple, Therefore, there are more red and black trees in practical application.
- AVLTree: strictly balanced binary search tree; RBTree: approximately balanced binary search tree.
- AVL does not necessarily rely on the balance factor, but introduces the balance factor for convenience, not necessarily with pair.
- AVL trees must be rotated, but red and black trees are not. Sometimes red and black trees only need to change the color of nodes.
- AVL tree is guaranteed by the balance factor of nodes, and red black tree is guaranteed by the color of nodes and the characteristics of red black tree.
- AVL trees are strictly balanced. Although red and black trees are approximately balanced, their performance is often better than AVL trees, and their implementation is simple. Therefore, their search efficiency is O(logN).