1 Array, Chain List
Mode 1 Static Initialization
int[] arr0 = new int[]{2,4,6,8};
Mode 2 implicit initialization
double[] arr1 = {2.2,3.3,4.4};
Mode 3 dynamic initialization
int[] arr2 = new int[3];//[3] means that this array can hold three elements
arr[0] = 2;//[0] The first data representing the array stores 2 in the first position of the array
arr[1] = 4;//[1] The second data representing the array Store 4 in the second position of the array
arr[2] = 6;//[2] The third data representing the array stores six in the third position of the array
Chain List: The process of creating a chain table is different from that of creating an array. A contiguous block of memory is not drawn out first. Because the data in a chain table is not contiguous, there are two areas in the memory where the data is stored, and one area where the data is stored. An area is used to record where the next data is stored (pointer to next data). When data enters the chain table, it finds the next location to store the data based on the pointer, saves the data, and then points to the next location to store the data. This allows the chain table to take advantage of some fragmentation space, although the chain table is a linear table, it does not store the data in a linear order.

Expanding the knowledges: ArrayList and linklist.
At present, I use arraylist more often, after all, many small open source projects only ensure that the program can run, whether it is good or bad, after all, small projects are not visible to the naked eye.
- ArrayList is based on arrays and LinkedList is based on double-linked lists. LinkedList is powerful as a two-way queue, stack, and List collection.
- Because Array is an index-based data structure, it is fast to search and read data in arrays using an index, and it can directly return elements in the index position of the array, so it has better performance in random access to collection elements. Array acquires data with O(1) time complexity, but inserting and deleting data is expensive. I also know roughly that the rest of the projects that are already in use in the market need to be contacted in order to better understand the use.
- LinkedList requires more memory because the location of each index in the ArrayList is the actual data, while each node in the LinkedList stores the actual data and the location of the front and back nodes.
2 Queues, Stacks
Queues: Queues are a first-in-first-out data structure, and arrays and chain tables can also generate queues. When data enters a queue, it enters below first and then above first, but when it comes out of the queue, it first exits below, then above, and lastly enters and exits the queue.

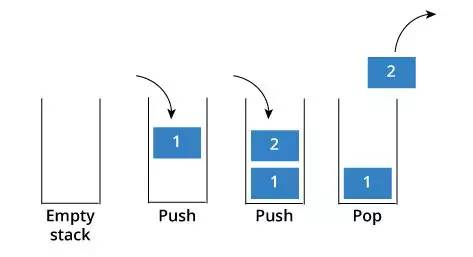
Stack: A stack is a FIFO data structure that can be generated from arrays and lists. When the data enters the stack, it will be pushed to the bottom of the stack according to the rules, then the data that enters again will be pushed on the first data, and so on, when the data in the stack is taken out, the top data will be taken out first, so it is first come out.
Since both arrays and lists can form a stack, the operating characteristics depend on whether the stack is generated from an array or a list, and the corresponding operating characteristics will be inherited.
3 Trees, Heaps, Diagrams
Tree: A tree refers specifically to a binary tree. A binary tree is a finite set of n (n>=0) nodes, either an empty set (empty binary tree), or a binary tree consisting of a root node and two disjoint left and right subtrees called root nodes, respectively.
- Each node has at most two subtrees. (Note: Instead of requiring two subtrees, you can have at most two, neither a subtree nor a subtree.)
- The left subtree and the right subtree are sequential and cannot be reversed.
- Even if a node in a tree has only one subtree, it is necessary to distinguish whether it is a left subtree or a right subtree. Below is a completely different binary tree:

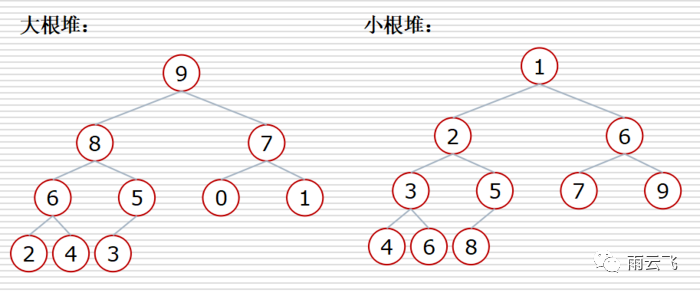
Heap: A heap is a complete binary tree. In this tree, all parent nodes satisfy a heap called a large root heap that is greater than or equal to their child nodes. All parent nodes satisfy a heap called a small root heap that is less than or equal to their child nodes. A heap is a tree, but it is usually stored in an array where parent-child relationships are determined by the array subscripts.
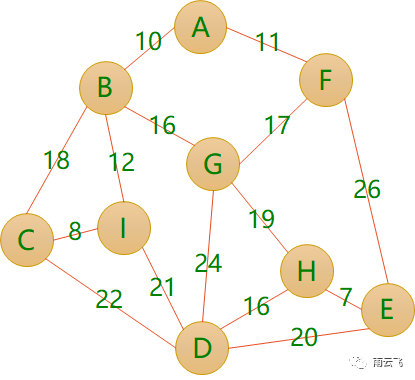
**Diagram: **Graph is a graph composed of an infinite non-empty set of vertices and a set of edges between vertices, usually expressed as G(V,E), where G represents a graph, V is a set of vertices in graph G, and E is a set of edges in graph G. Graphs come in all shapes and sizes. Edges can have weight s, where each edge is assigned a positive or negative value.
4 Hash Table
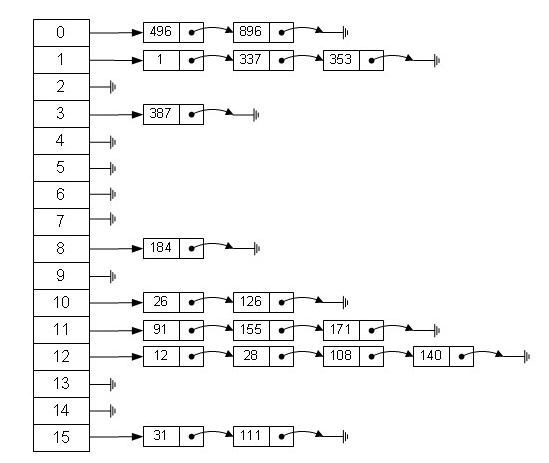
Hash tables are also common in applications. For example, some collection classes in Java are constructed by using hash principles, such as HashMap, HashTable, etc. With the advantages of hash tables, it is very convenient to find elements for a collection. However, because hash tables are array-based data structures, they are slower to add and delete elements. So many times you need to use an array chain table, which is called zipper method. Zipper method is a structure of array-bound chain lists, which were used in the lower storage of earlier hashMaps until jdk1.8 and then the structure of the array plus the red-black tree is changed. The following is an example:
Extension knowledges: hashmap and hashtable (omitted)
57 Basic Sorts
Comparing the various indexes of the seven sorting algorithms (the most common), stability is only between two
(Do not remember tables, remember sorting rules, this order is easy to remember, remember dynamic charts)
| Sorting method | Average | Best case | Worst case | Spatial Complexity | stability |
|---|---|---|---|---|---|
| Bubble sort | O(n²) | O(n) | O(n²) | O(1) | Stable |
| Insert Sort | O(n²) | O(n) | O(n²) | O(1) | Stable |
| Select Sort | O(n²) | O(n²) | O(n²) | O(1) | Stable |
| Merge Sort | O(n logn) | O(n logn) | O(n logn) | O(n) | Stable |
| Heap Sorting | O(n logn) | O(n logn) | O(n logn) | O(1) | Instable |
| Quick Sort | O(n logn) | O(n logn) | O(n²) | O(logn)~O(n) | Instable |
| Shell Sort | O(n logn)~O(n²) | O(n^1.3~1.5) | O(n²) | O(1) | Instable |
5.1 Bubble Sorting
Compare two to two, big back row, so it's o(n) ²), If you start out sorted, and only do a two-to-two comparison once, n o exchange is o(n)
5.2 Insert Sort Directly
Take the next number and compare it with the previous one. Play it behind it. If it is sorted at the beginning, just take out and insert it. If it is not compared with the previous one, it is o(n).
5.3 Half Insert Sort:

5.4 Select Sort
Find the smallest, put the front, all once, two times for overlay, so is o(n) ²)
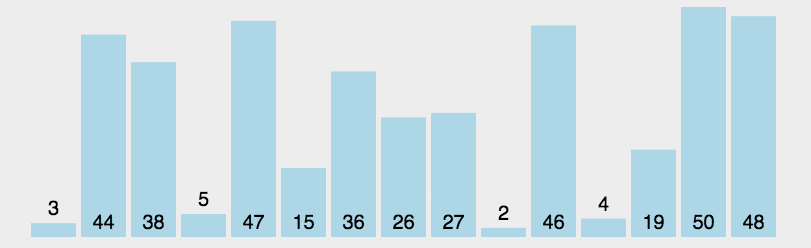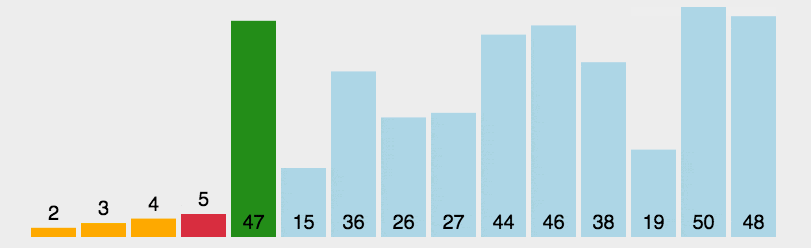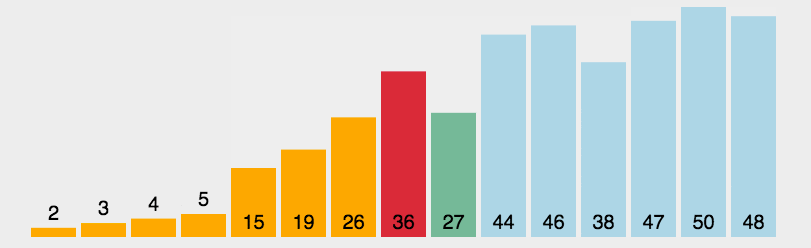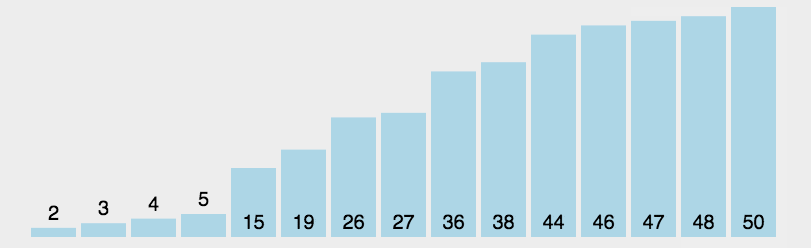
5.5 Merge Sort
Sort from smallest to largest, first make each number in the array a single interval of length 1, then merge two or two groups in order to get an ordered interval of length 2, and proceed one by one until the entire interval is synthesized.
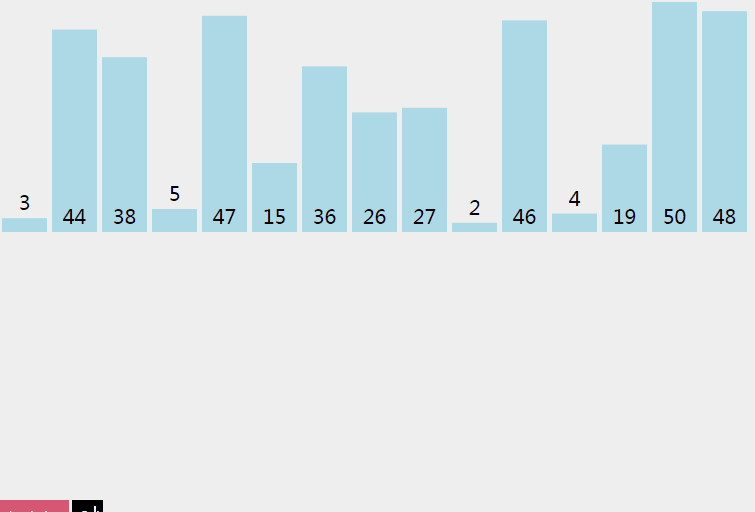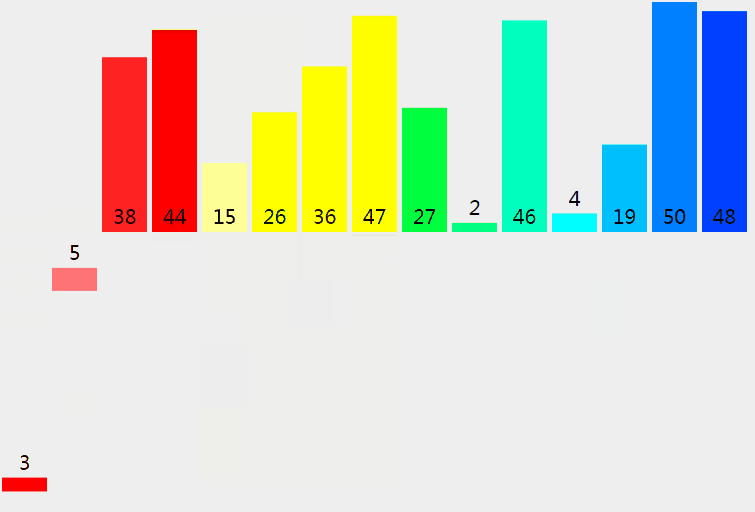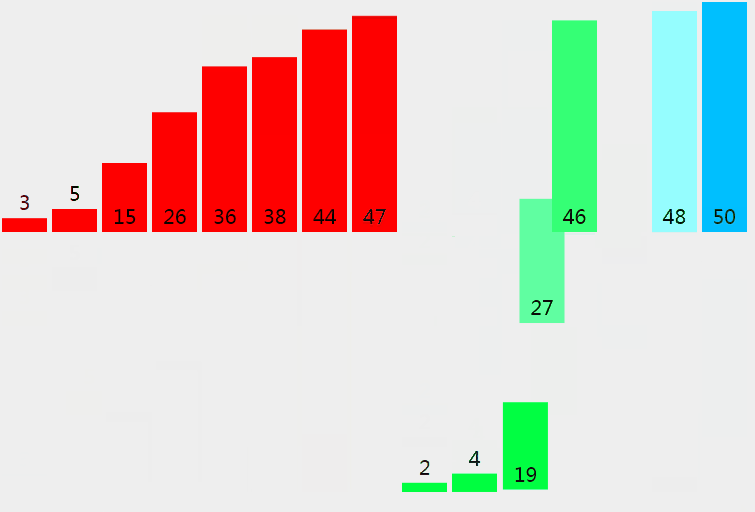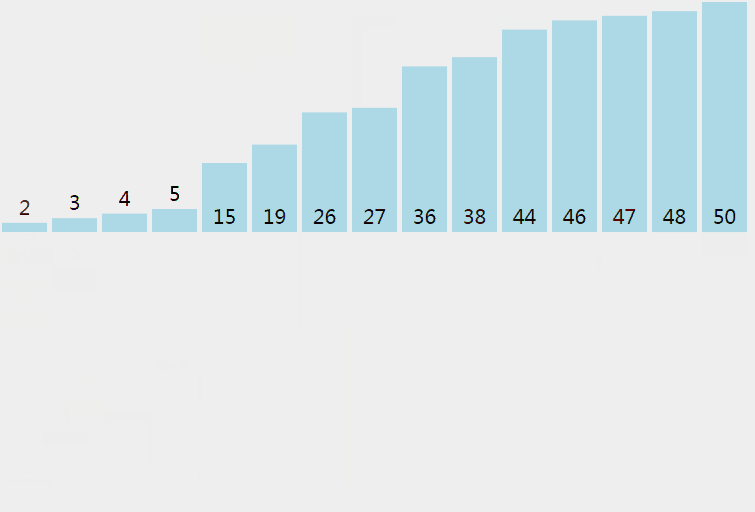
5.6 Quick Sort
Sort from smallest to largest: a base number, less than the base number to the left, larger to the right
Randomly select a number in the array (the first element of the default array). Place less than or equal to the number on the left, greater than the number on the right, and recursively call Quick Sort on both sides of the array to repeat the process.
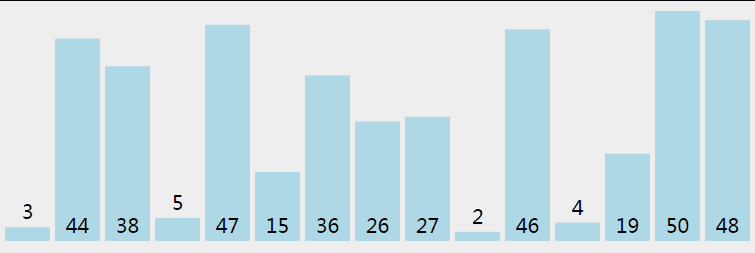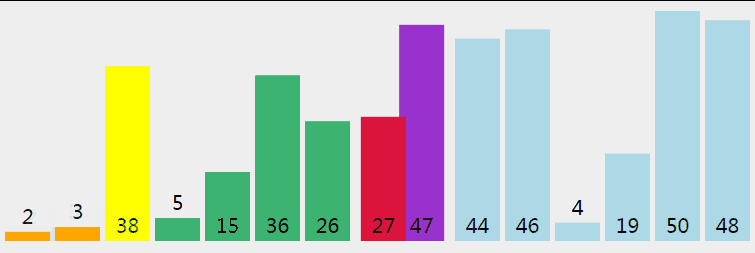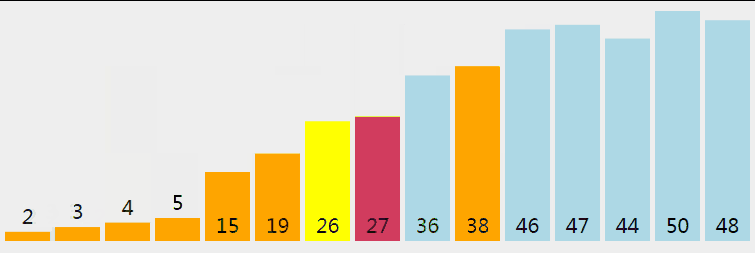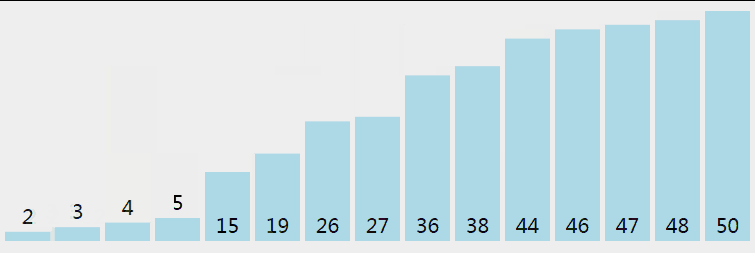
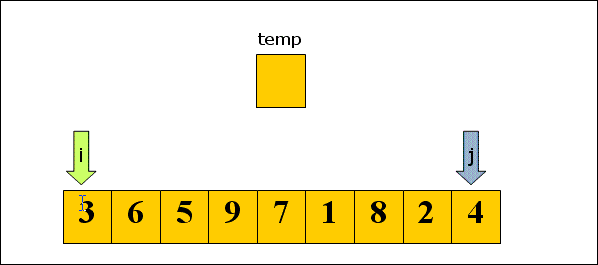
5.7 Hill Sort
First, the whole sequence of records to be sorted is divided into several subsequences and inserted into the sorting font> directly. The algorithm is described in detail:

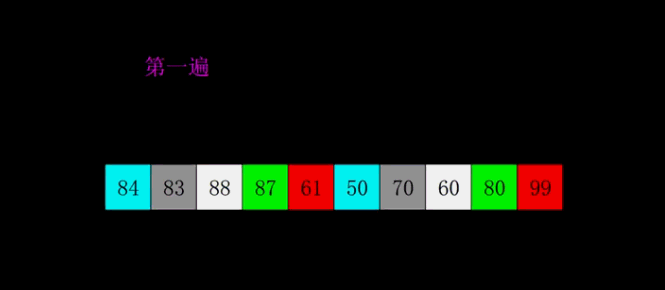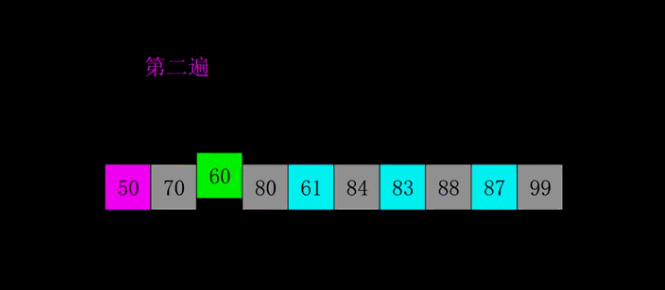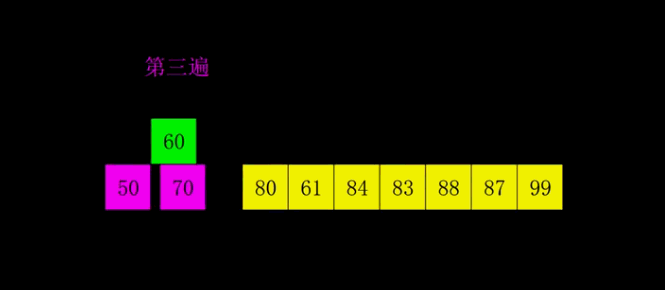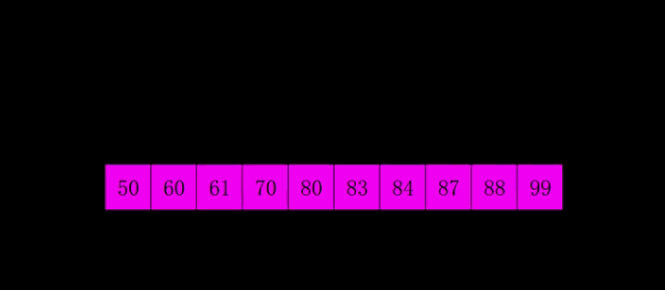
6 Simple Algorithms
6.1 Bubble Sorting
public static int[] bubbleSort(int[] array){
if(array.length > 0){
for(int i = 0;i<array.length;i++){
for(int j = 0;j<array.length - 1 - i;j++){
if(array[j] > array[j+1]){
int temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
}
}
}
return array;
}
6.2 Insert Sort Directly
public static int[] insertionSort(int[] array) {
if (array.length == 0)
return array;
int current;
for (int i = 0; i < array.length - 1; i++) {
current = array[i + 1];
int preIndex = i;
while (preIndex >= 0 && current < array[preIndex]) {
array[preIndex + 1] = array[preIndex];
preIndex--;
}
array[preIndex + 1] = current;
}
return array;
}
6.3 Select Sort
public static int[] selectionSort(int[] array) {
if (array.length == 0)
return array;
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i; j < array.length; j++) {
if (array[j] < array[minIndex]) //Find the smallest number
minIndex = j; //Save Minimum Index
}
int temp = array[minIndex];
array[minIndex] = array[i];
array[i] = temp;
}
return array;
}
6.4 Merge Sort
public static int[] MergeSort(int[] array) {
if (array.length < 2) return array;
int mid = array.length / 2;
int[] left = Arrays.copyOfRange(array, 0, mid);
int[] right = Arrays.copyOfRange(array, mid, array.length);
return merge(MergeSort(left), MergeSort(right));
}
public static int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
for (int index = 0, i = 0, j = 0; index < result.length; index++) {
if (i >= left.length)
result[index] = right[j++];
else if (j >= right.length)
result[index] = left[i++];
else if (left[i] > right[j])
result[index] = right[j++];
else
result[index] = left[i++];
}
return result;
}
6.5 Quick Sort
public static int[] QuickSort(int[] array, int start, int end) {
if (array.length < 1 || start < 0 || end >= array.length || start > end) return null;
int smallIndex = partition(array, start, end);
if (smallIndex > start)
QuickSort(array, start, smallIndex - 1);
if (smallIndex < end)
QuickSort(array, smallIndex + 1, end);
return array;
}
//Quick sorting algorithm
public static int partition(int[] array, int start, int end) {
int pivot = (int) (start + Math.random() * (end - start + 1));
int smallIndex = start - 1;
swap(array, pivot, end);
for (int i = start; i <= end; i++)
if (array[i] <= array[end]) {
smallIndex++;
if (i > smallIndex)
swap(array, i, smallIndex);
}
return smallIndex;
}
//Swap two elements in an array
public static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
6.6 Hill Sort
public static int[] ShellSort(int[] array) {
int len = array.length;
int temp, gap = len / 2;
while (gap > 0) {
for (int i = gap; i < len; i++) {
temp = array[i];
int preIndex = i - gap;
while (preIndex >= 0 && array[preIndex] > temp) {
array[preIndex + gap] = array[preIndex];
preIndex -= gap;
}
array[preIndex + gap] = temp;
}
gap /= 2;
}
return array;
}
6.7 Other algorithms, low priority
Algorithms are important, but they have low priority and are delayed strategically because they cannot make up for them in a short time.
7 Reference Links
Array definition, declaration, initialization, traversal, bubble sort: https://blog.csdn.net/qq_43519384/article/details/106203666
Data Structure and Algorithms for High Frequency Surface Meridians: https://blog.csdn.net/qq_36936730/article/details/104342464
Top 10 Classic Sorting Algorithms are the strongest summaries (with JAVA code implementations): https://blog.csdn.net/sinat_38325967/article/details/88851025
If there are any omissions, leave a message in the comments area.