1. Concept of red black tree
Red Black tree is a binary search tree, but a storage bit is added on each node to represent the color of the node, which can be red or Black. By limiting the coloring mode of each node on any path from root to leaf, the red Black tree ensures that no path will be twice longer than other paths, so it is close to balance.
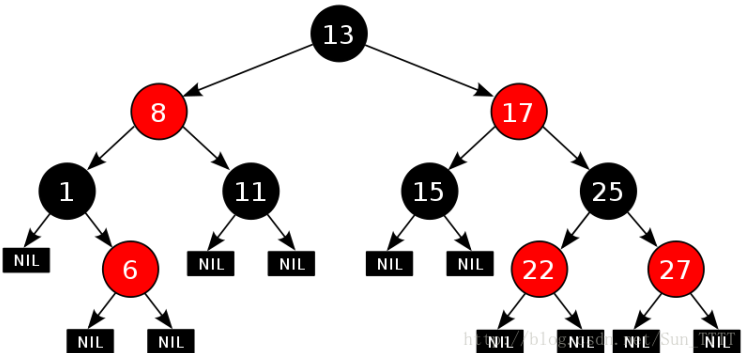
2. Properties of red black tree
- Each node is either red or black
- The root node is black
- If a node is red, its two child nodes are black (there cannot be two consecutive red nodes)
- For each node, the simple path from this node to all its descendant leaf nodes contains the same number of black nodes
- Each leaf node is black (the leaf node here refers to the empty node)
3. Definition of red black tree node
In the definition of node, why should the default color of node be red?
When you have to choose one of the destructive properties 3 and 4, choose destructive property 3 (a red node and its two child nodes are black). This condition is relatively easier to control and ensure that the number of black nodes on each path is the same. This condition is not easy to control.
enum Color
{
RED,
BLACK
};
template<class K,class V>
struct RBTreeNode
{
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
pair<K, V> _kv;
enum Color _col;
//When you have to choose one of destructive properties 3 and 4, it is better to choose 3 - a red node and his two children's nodes are black
RBTreeNode(const pair<K,V>& kv)
: _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _col(RED)
, _kv(kv)
{}
};
4. Red black tree insertion
The red black tree is based on the binary search tree with its balance constraints. Therefore, the insertion of red black tree can be divided into two steps:
- Insert new nodes according to the tree rules of binary search
- Detect whether the nature of red black tree is damaged after the new node is inserted
Inserting new nodes can be divided into two cases according to the large frame:
- This node exists and is red
- The uncle node does not exist or exists and is black
Because the default color of the new node is red, if the color of its parent node is black and does not violate any property of the red black tree, it does not need to be adjusted; However, when the color of the parent node of the newly inserted node is red, it violates property 3 and cannot have connected red nodes. At this time, it is necessary to discuss the red black tree according to the situation:
Convention: cur is the current node, p is the parent node, g is the grandfather node, and u is the uncle node
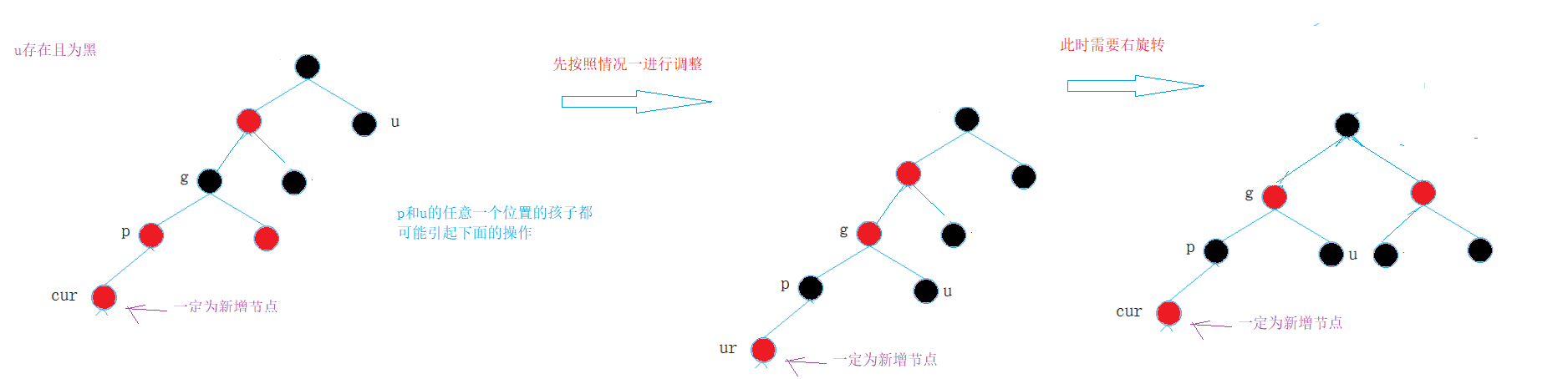
Case 1: cur is red, p is red, g is black, and u exists and is red
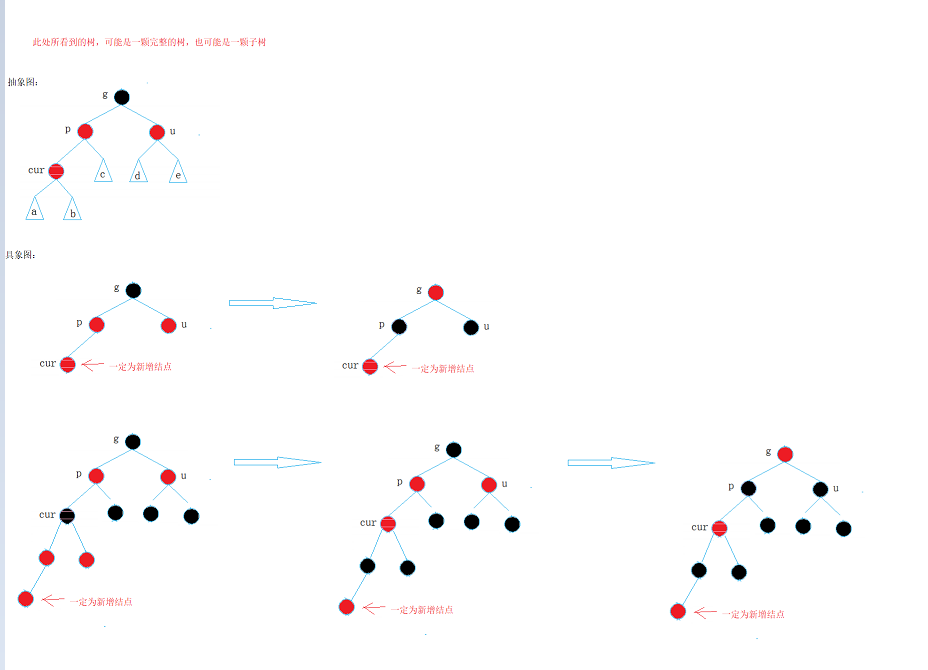
- p and u become black and g becomes red. In this way, there will be no continuous red nodes, and the number of black nodes in each path of this subtree will not change.
- If G is the root node, change g to black after adjustment.
- If g is a subtree, g must have parents, and if g's parents are red, they need to continue to adjust upward
Case 2: cur is red, p is red, g is black, u does not exist / u exists and is black
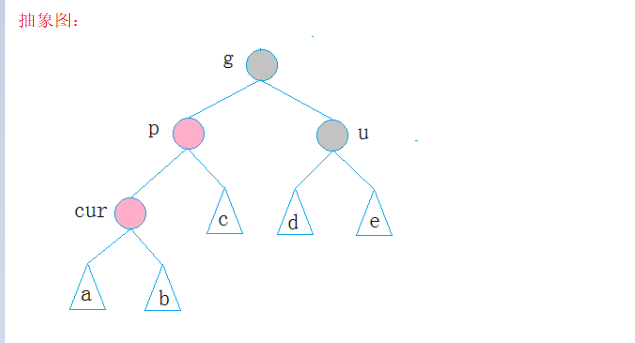
There are two situations of u:
- If u node does not exist, cur must be a newly inserted node, because if cur is not a newly inserted node, one of cur and p must be black, which does not meet property 4: the number of black nodes in each path is the same.
① Right single rotation
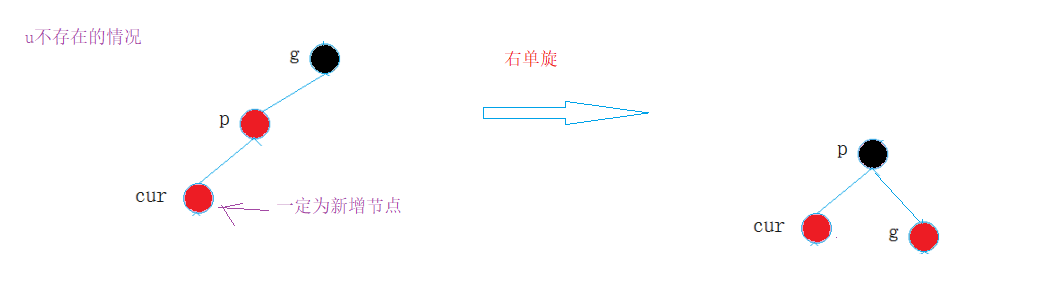
② Sinistral
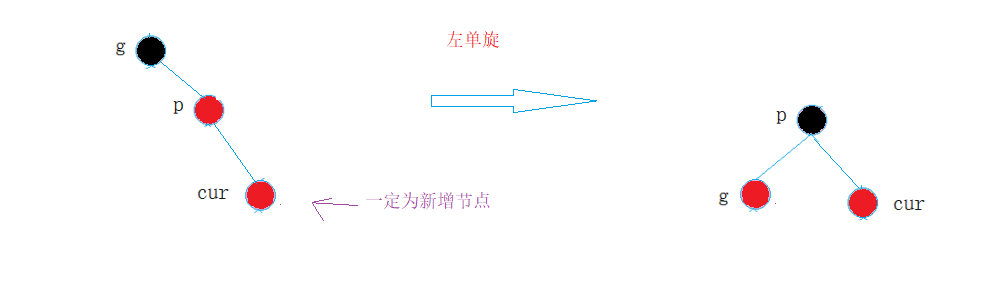
- If u node exists, it must be black, and the original color of cur node must be black.
Summary:
- If p is the left child of g and cur is the left child of p, perform right single rotation;
- If p is the right child of g and cur is the right child of p, carry out left single rotation
- p. g discoloration – P turns black and g turns red
There are two situations of u:
- If u node does not exist, cur must be a newly inserted node, because if cur is not a newly inserted node, one of cur and p must be black, which does not meet property 4: the number of black nodes in each path is the same.
- If u node exists, it must be black, and the original color of cur node must be black
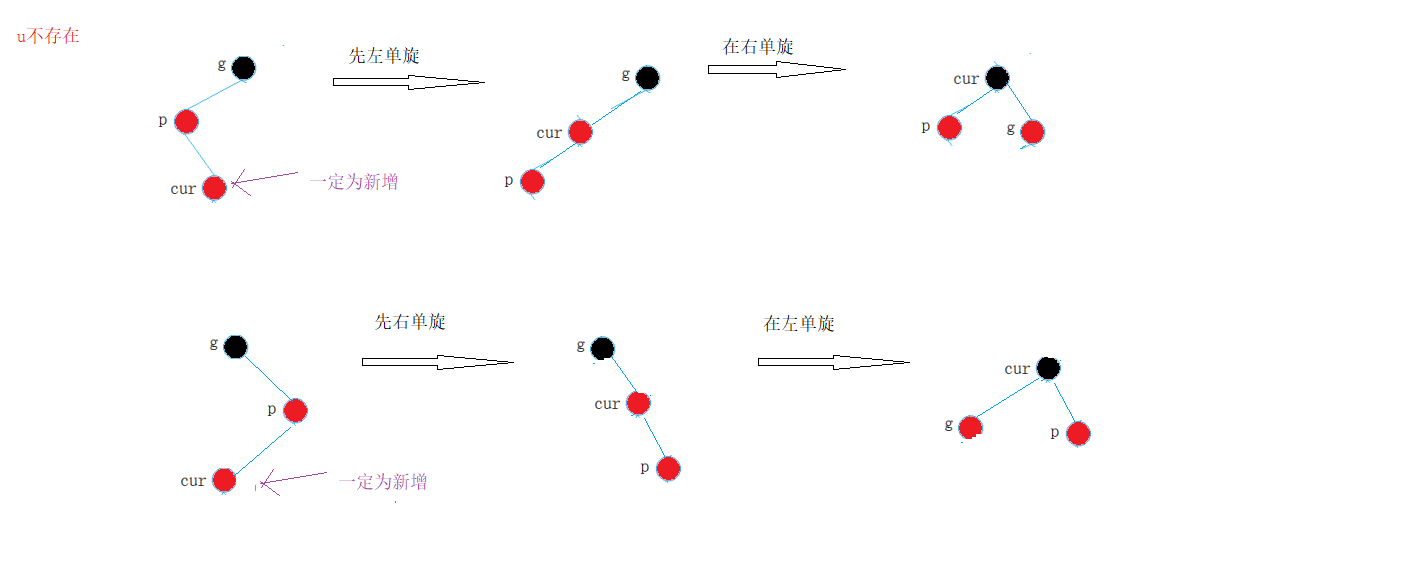
③ First left single rotation and then right single rotation
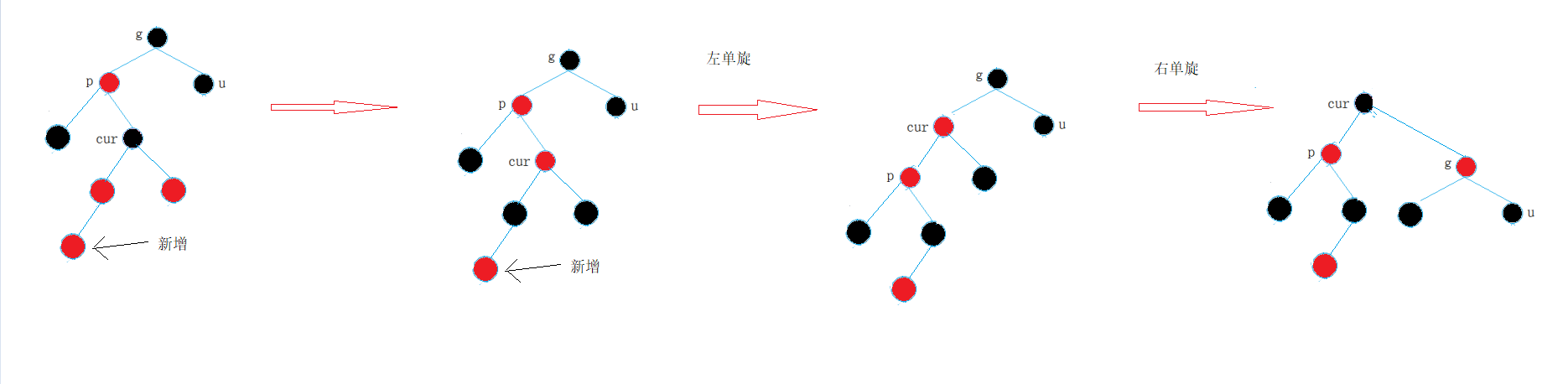
④ First right single rotation and then left single rotation
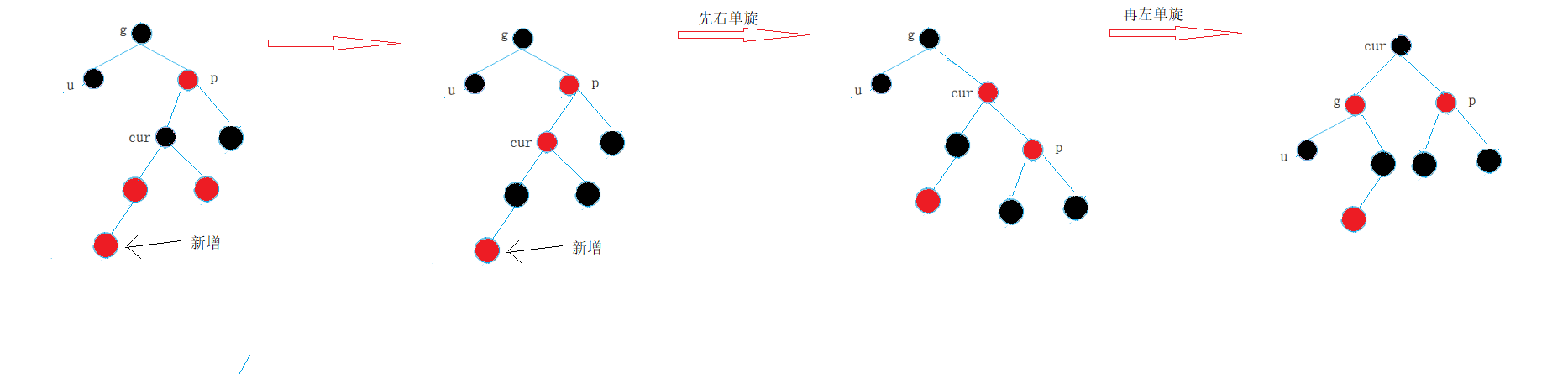
Summary:
- If p is the left child of g and cur is the right child of p, make a left single rotation for p, and then make a right single rotation with cur;
- If p is the right child of g and cur is the left child of p, make a right single rotation for p, and then make a left single rotation with cur;
- g turns red and cur turns black
pair<Node*,bool> Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return make_pair(_root, true);
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(cur, false);
}
}
cur = new Node(kv);//RED
//This indicates that the location has been found and needs to be inserted
if (parent->_kv.first < kv.first)
{
//This indicates that the link should be on the right side of the parent node
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
Node* newnode = cur;
//Because the default color of the new node is red, if the color of its parent node is black and does not violate any property of the red black tree, it does not need to be adjusted
while (parent && parent->_col == RED) //cur is new. There must be a parent, but if it jumps up one level, there will be no parent
{
Node* grandfather = parent->_parent;
if (grandfather->_left == parent)
{
Node* uncle = grandfather->_right;
//Case 1: the uncle exists and is red. In the first case, it does not rotate, but simply changes one color
if (uncle && uncle->_col == RED)
{
//Discoloration
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//Continue to process upward
cur = grandfather;
parent = cur->_parent;
}
else //Case 2+3 u does not exist or exists and is black
{
// g
// p
// c
if (cur == parent->_left)//Right single rotation
{
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
//This is a double spin
// g
// p
// c
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else //grandfather->_right == parent
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)
{
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;//Don't forget here that it is also possible to continue to process iteratively
}
else
{
//Uncle doesn't exist or uncle's color is black
// g
// p
// c
if (cur == parent->_right)
{
RotateL(grandfather);
grandfather->_col = RED; //
parent->_col = BLACK;
}
// g
// p
// c
else
{
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;//Always turn the root black
return make_pair(newnode, true);
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
//But the subLR may be empty, so the following code will crash
if (subLR)
subLR->_parent = parent;
Node* parentParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
//At this time, the last step is to replace the root node
if (parent == _root)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
//At this time, you need to connect the node 30, but you still need to judge which side it should be connected to
if (parentParent->_left == parent)
{
parentParent->_left = subL;
}
else
{
parentParent->_right = subL;
}
subL->_parent = parentParent;
}
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* parentParent = parent->_parent;//Save it first, because this will be changed later, and the initial parent node cannot be found
subR->_left = parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
//As part of a subtree
if (parentParent->_left == parent)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
subR->_parent = parentParent;
}
}
5. Verification of red black tree
The detection of red black tree is divided into two steps:
- Check whether it meets the binary search tree (whether the middle order traversal is an ordered sequence)
- Check whether it meets the property of red black tree (of course, you can also check whether the longest path will not exceed twice the shortest path, but this condition is relatively difficult to check, so here you choose to check whether the tree meets the property)
void _Inorder(Node* root)
{
if (root == nullptr)
return;
_Inorder(root->_left);
cout << root->_kv.first << " ";
_Inorder(root->_right);
}
void Inorder()
{
_Inorder(_root);
cout << endl;
}
bool _CheckRedCol(Node* root)
{
if (root == nullptr)
return true;
if (root->_col == RED)
{
Node* parent = root->_parent;
if (parent->_col == RED)
{
cout << "Violation rule 3: there are continuous red nodes" << endl;
return false;
}
}
return _CheckRedCol(root->_left) && _CheckRedCol(root->_right);
}
//Check whether the number of black nodes on each path is the same
bool _CheckBlackNum(Node* root,int blackNum,int trueNum)
{
if (root == nullptr)
{
return trueNum == blackNum;
}
if (root->_col == BLACK)
{
blackNum++;
}
return _CheckBlackNum(root->_left, blackNum,trueNum) && _CheckBlackNum(root->_right, blackNum,trueNum);
}
//Don't consider checking whether the longest path is no more than twice the shortest path. This method is troublesome
//But from the reverse thinking, check whether his nature is satisfied
bool IsBalance()
{
if (_root && _root->_col == RED)
{
cout << "Violation rule 1: the root node is red" << endl;
return false;
}
int trueNum = 0; //Get the node value on the real path, and then compare it with the calculated one
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
{
++trueNum;
}
cur = cur->_left;
}
int blackNum = 0;
return _CheckRedCol(_root) && _CheckBlackNum(_root, blackNum,trueNum); //In this way, we can know whether all the properties of red black tree are satisfied
}
6. Comparison between red black tree and AVL tree
Both red black trees and AVL trees are efficient balanced binary trees. The time complexity of adding, deleting, modifying and checking is O(logN) (based on 2). Red black trees do not pursue absolute balance. They only need to ensure that the longest path does not exceed twice the shortest path. Relatively speaking, the number of insertion and rotation is reduced. Therefore, in the structure of frequent addition and deletion, the neutral energy is better than AVL trees, (AVL tree is a strictly balanced binary search tree, while red black tree is only an approximately balanced binary search tree, but in terms of efficiency, the two are almost the same from the perspective of computer). Moreover, the implementation of red black tree is relatively simple, so there are more red black trees in practical application.
7. Complete red black tree simulation implementation code
#include<iostream>
using namespace std;
enum Color
{
RED,
BLACK
};
template<class K,class V>
struct RBTreeNode
{
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
pair<K, V> _kv;
enum Color _col;
//When you have to choose one of destructive properties 3 and 4, it is better to choose 3 - a red node and his two children's nodes are black
RBTreeNode(const pair<K,V>& kv)
: _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _col(RED)
, _kv(kv)
{}
};
template<class K,class V>
class RBTree
{
typedef RBTreeNode<K, V> Node;
public:
pair<Node*,bool> Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return make_pair(_root, true);
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(cur, false);
}
}
cur = new Node(kv);//RED
//This indicates that the location has been found and needs to be inserted
if (parent->_kv.first < kv.first)
{
//This indicates that the link should be on the right side of the parent node
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
Node* newnode = cur;
//Because the default color of the new node is red, if the color of its parent node is black and does not violate any property of the red black tree, it does not need to be adjusted
while (parent && parent->_col == RED) //cur is new. There must be a parent, but if it jumps up one level, there will be no parent
{
Node* grandfather = parent->_parent;
if (grandfather->_left == parent)
{
Node* uncle = grandfather->_right;
//Case 1: the uncle exists and is red. In the first case, it does not rotate, but simply changes one color
if (uncle && uncle->_col == RED)
{
//Discoloration
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//Continue to process upward
cur = grandfather;
parent = cur->_parent;
}
else //Case 2+3 u does not exist or exists and is black
{
// g
// p
// c
if (cur == parent->_left)//Right single rotation
{
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
//This is a double spin
// g
// p
// c
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else //grandfather->_right == parent
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)
{
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;//Don't forget here that it is also possible to continue to process iteratively
}
else
{
//Uncle doesn't exist or uncle's color is black
// g
// p
// c
if (cur == parent->_right)
{
RotateL(grandfather);
grandfather->_col = RED; //
parent->_col = BLACK;
}
// g
// p
// c
else
{
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;//Always turn the root black
return make_pair(newnode, true);
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
//But the subLR may be empty, so the following code will crash
if (subLR)
subLR->_parent = parent;
Node* parentParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
//At this time, the last step is to replace the root node
if (parent == _root)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
//At this time, you need to connect the node 30, but you still need to judge which side it should be connected to
if (parentParent->_left == parent)
{
parentParent->_left = subL;
}
else
{
parentParent->_right = subL;
}
subL->_parent = parentParent;
}
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* parentParent = parent->_parent;//Save it first, because this will be changed later, and the initial parent node cannot be found
subR->_left = parent;
parent->_parent = subR;
if (parent == _root)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
//As part of a subtree
if (parentParent->_left == parent)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
subR->_parent = parentParent;
}
}
void _Inorder(Node* root)
{
if (root == nullptr)
return;
_Inorder(root->_left);
cout << root->_kv.first << " ";
_Inorder(root->_right);
}
void Inorder()
{
_Inorder(_root);
cout << endl;
}
bool _CheckRedCol(Node* root)
{
if (root == nullptr)
return true;
if (root->_col == RED)
{
Node* parent = root->_parent;
if (parent->_col == RED)
{
cout << "Violation rule 3: there are continuous red nodes" << endl;
return false;
}
}
return _CheckRedCol(root->_left) && _CheckRedCol(root->_right);//In fact, the problem of splitting into roots, left subtrees and right subtrees
}
bool _CheckBlackNum(Node* root,int blackNum,int trueNum)
{
if (root == nullptr)
{
return trueNum == blackNum;//Compare the calculated with the real one
}
if (root->_col == BLACK)
{
blackNum++;
}
return _CheckBlackNum(root->_left, blackNum,trueNum) && _CheckBlackNum(root->_right, blackNum,trueNum);
}
//Don't consider checking whether the longest path is no more than twice the shortest path. This method is troublesome
//But from the reverse thinking, check whether his nature is satisfied
bool IsBalance()
{
if (_root && _root->_col == RED)
{
cout << "Violation rule 1: the root node is red" << endl;
return false;
}
int trueNum = 0; //Get the node value on the real path, and then compare it with the calculated one
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
{
++trueNum;
}
cur = cur->_left;
}
int blackNum = 0;
return _CheckRedCol(_root) && _CheckBlackNum(_root, blackNum,trueNum); //In this way, we can know whether all the properties of red black tree are satisfied
}
private:
Node* _root = nullptr;
};
main.c
#include"RBTree.hpp"
void TestRBTree()
{
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
RBTree<int, int> t;
for (auto e : a)
{
t.Insert(make_pair(e, e));
}
t.Inorder();
cout << t.IsBalance() << endl;
}
int main()
{
TestRBTree();
}
