1, Simple sort
1.1 introduction to comparable interface
Since we are going to talk about sorting here, we will certainly compare between elements, and Java provides an interface, Comparable, which is used to define sorting
Rules. Here we briefly review the Comparable interface in the form of a case.
Requirements:
1. Define a Student class with age and username attributes, and provide comparison rules through the Comparable interface;
2. Define the Test class Test, and define the Test method Comparable getMax(Comparable c1,Comparable c2) in the Test class Test to complete the Test.
// 1. Define a Student class with age and username attributes, and provide comparison rules through the Comparable interface;
public class Student implements Comparable<Student> {
private String username;
private int age;
@Override
public String toString() {
return "Student{" +
"username='" + username + '\'' +
", age=" + age +
'}';
}
public Student(String username, int age) {
this.username = username;
this.age = age;
}
public String getUsername() {
return username;
}
public void setUsername(String username) {
this.username = username;
}
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
public int compareTo(Student o) {
return this.getAge()-o.getAge();
}
}
// 2. Define the Test class Test, and define the Test method Comparable getMax(Comparable c1,Comparable c2) in the Test class Test to complete the Test
public class TestComparable {
public static Comparable getMax(Comparable c1,Comparable c2){
int result = c1.compareTo(c2);
// If result < 0, c1 is smaller than c2
// If result > 0, c1 is larger than c2
// If result==0, c1 is as large as c2
if (result>=0) {
return c1;
}else{
return c2;
}
}
public static void main(String[] args) {
Student s1 = new Student("zs",18);
Student s2 = new Student("ls",20);
Comparable max = getMax(s1, s2);
System.out.println(max);
}
}
Output: Student{username='ls', age=20}
1.2 bubble sorting
Bubble Sort is a relatively simple sorting algorithm in the field of computer science.
Requirements:
Before sorting: {4,5,6,3,2,1}
After sorting: {1,2,3,4,5,6}
Sorting principle:
-
Compare adjacent elements. If the previous element is larger than the latter, the positions of the two elements are exchanged.
-
Do the same for each pair of adjacent elements, from the first pair of elements to the last pair of elements at the end. The element in the final position is the largest
Value.

Bubble sorting API design:
| Class name | Bubble |
|---|---|
| Construction method | Bubble(): creates a bubble object |
| Member method | 1.public static void sort(Comparable[] a): sort the elements in the array 2.private static boolean greater(Comparable v,Comparable w): judge whether v is greater than W 3.private static void exch(Comparable[] a,int i,int j): exchange the values at index I and index J in array a |
Code implementation of bubble sorting:
public class Bubble {
/*
Sort the elements in array a
*/
public static void sort(Comparable[] a) {
// Maximum index
for (int i = a.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
// Compare the values at index j and index j+1
if (greater(a[j], a[j + 1])) {
exch(a, j, j + 1);
}
}
}
}
/*
Compare whether the v element is larger than the w element
*/
private static boolean greater(Comparable v, Comparable w) {
return v.compareTo(w) > 0;
}
/*
Array elements i and j swap positions
*/
private static void exch(Comparable[] a, int i, int j) {
Comparable temp;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
public class TestBubble {
public static void main(String[] args) {
Integer[] arr = {4,5,6,3,2,1};
Bubble.sort(arr);
System.out.println(Arrays.toString(arr));
}
}
Output:[1, 2, 3, 4, 5, 6]
Time complexity analysis of bubble sorting
Bubble sorting uses a double-layer for loop, in which the loop body of the inner loop is the code that really completes the sorting. Therefore, we analyze the time complexity of bubble sorting
For the complexity, mainly analyze the execution times of the inner loop.
In the worst case, that is, if the elements to be sorted are {6,5,4,3,2,1} in reverse order, then:
The number of element comparisons is:
(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;
The number of element exchanges is:
(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;
The total number of executions is:
(N2/2-N/2)+(N2/2-N/2)=N^2-N;
According to the large o derivation rule, if the highest order term in the function is retained, the time complexity of the final bubble sorting is O(N^2)
1.3 selection and sorting
Selective sorting is a more simple and intuitive sorting method.
Requirements:
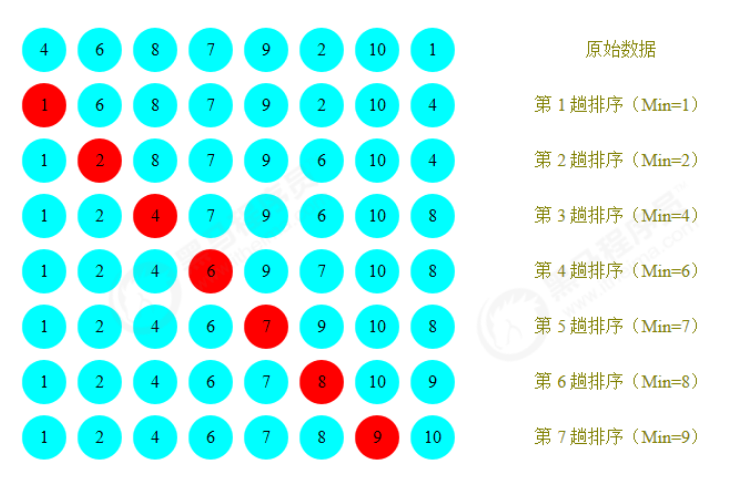
Before sorting: {4,6,8,7,9,2,10,1}
After sorting: {1,2,4,5,7,8,9,10}
Sorting principle:
1. During each traversal, it is assumed that the element at the first index is the minimum value, and it is compared with the values at other indexes in turn. If the current index
If the value at is greater than the value at some other index, it is assumed that the value derived from some other index is the minimum value. Finally, the index where the minimum value is located can be found
2. Exchange the values at the first index and the index where the minimum value is located
Select Sorting API design:
| Class name | Selection |
|---|---|
| Construction method | Selection(): create a selection object |
| Member method | 1.public static void sort(Comparable[] a): sort the elements in the array 2.private static boolean greater(Comparable v,Comparable w): judge whether v is greater than W 3.private static void exch(Comparable[] a,int i,int j): exchange the values at index I and index J in array a |
Select the code implementation for sorting:
public class Selection {
/*
Sort the elements in array a
*/
public static void sort(Comparable[] a) {
for (int i = 0; i < a.length - 1; i++) {
// Define a variable to record the index of the smallest element. By default, it is the location of the first element participating in the selection sorting
int minIndex = i;
for (int j = i + 1; j < a.length; j++) {
// You need to compare the value at the minimum index minIndex with the value at the j index
if (greater(a[minIndex], a[j])) {
minIndex = j;
}
}
// Swap the value at index minIndex where the smallest element is located and the value at index i
exch(a, i, minIndex);
}
}
/*
Compare whether the v element is greater than w
*/
private static boolean greater(Comparable v, Comparable w) {
return v.compareTo(w) > 0;
}
/*
Array elements i and j swap positions
*/
private static void exch(Comparable[] a, int i, int j) {
Comparable temp;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
public class TestSelection {
public static void main(String[] args) {
Integer[] arr = {4, 6, 8, 7, 9, 2, 10, 1};
Selection.sort(arr);
System.out.println(Arrays.toString(arr));
}
}
Output:[1, 2, 4, 6, 7, 8, 9, 10]
Select the time complexity analysis for sorting:
The selection sorting uses a double-layer for loop, in which the outer loop completes data exchange and the inner loop completes data comparison, so we make statistics respectively
Exchange times and data comparison times:
Data comparison times:
(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;
Data exchange times:
N-1
Time complexity: N2/2-N/2 + (N-1) = N2/2+N/2-1;
According to the large o derivation rule, the highest order term is retained and the constant factor is removed. The time complexity is O(N^2);
1.4 insert sort
Insertion sort is a simple, intuitive and stable sorting algorithm.
Insertion sort works much like people sort a hand of poker. At first, our left hand is empty and the cards on the table face down. Then, I
They take a card from the table one at a time and insert it in the correct position in their left hand. In order to find the correct position of a card, we compare it with the one already in the card from right to left
Compare each card in your hand, as shown in the figure below:

Requirements:
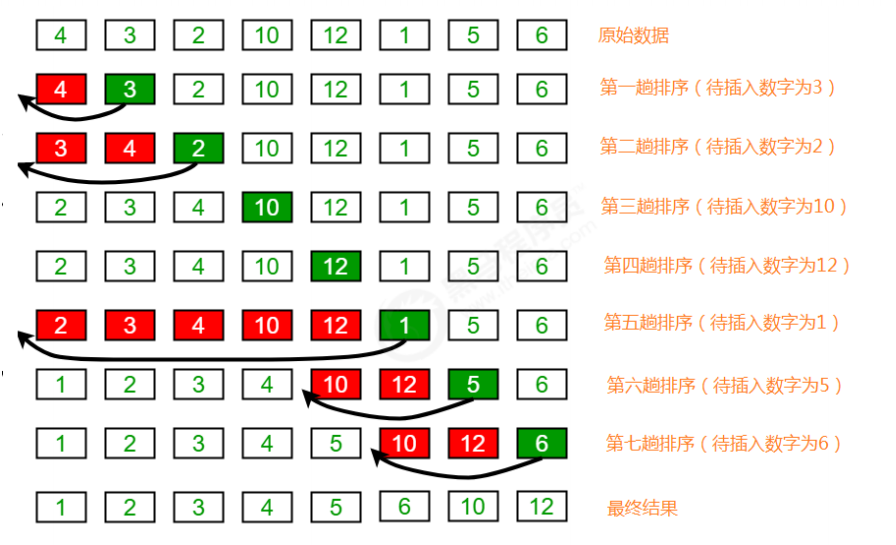
Before sorting: {4,3,2,10,12,1,5,6}
After sorting: {1,2,3,4,5,6,10,12}
Sorting principle:
1. Divide all elements into two groups, sorted and unordered;
2. Find the first element in the unordered group and insert it into the sorted group;
3. Flashback traverses the sorted elements and compares them with the elements to be inserted in turn until an element less than or equal to the element to be inserted is found
Insert the element in this position, and the other elements move back one bit;
Insert sort API design:
| Class name | Insertion |
|---|---|
| Construction method | Insertion(): create an insertion object |
| Member method | 1.public static void sort(Comparable[] a): sort the elements in the array 2.private static boolean greater(Comparable v,Comparable w): judge whether v is greater than W 3.private static void exch(Comparable[] a,int i,int j): exchange the values at index I and index J in array a |
Insert sort code implementation:
public class Insertion {
/*
Sort the elements in array a
*/
public static void sort(Comparable[] a) {
for (int i = 1; i <a.length ; i++) {
for (int j = i; j >0 ; j--) {
// Compare the value at index j with the value at index j-1. If the value at index j-1 is larger than the value of index j, exchange data. If it is not large, find a suitable location and exit the loop
if (greater(a[j-1],a[j])){
exch(a,j-1,j);
}else{
break;
}
}
}
}
/*
Compare whether the v element is greater than w
*/
private static boolean greater(Comparable v, Comparable w) {
return v.compareTo(w) > 0;
}
/*
Array elements i and j swap positions
*/
private static void exch(Comparable[] a, int i, int j) {
Comparable temp;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
public class TestInsertion {
public static void main(String[] args) {
Integer[] arr = {4, 3, 2, 10, 12, 1, 5, 6};
Insertion.sort(arr);
System.out.println(Arrays.toString(arr));
}
}
Output:[1, 2, 3, 4, 5, 6, 10, 12]
Time complexity analysis of insertion sort
Insertion sorting uses a double-layer for loop, in which the loop body of the inner loop is the code that really completes sorting. Therefore, we analyze the time complexity of insertion sorting
For complexity, mainly analyze the execution times of the inner loop.
In the worst case, the array elements to be sorted are {12,10,6,5,4,3,2,1}, then:
The number of comparisons is:
(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;
The number of exchanges is:
(N-1)+(N-2)+(N-3)+...+2+1=((N-1)+1)*(N-1)/2=N^2/2-N/2;
The total number of executions is:
(N2/2-N/2)+(N2/2-N/2)=N^2-N;
According to the large o derivation rule, if the highest order term in the function is retained, the time complexity of the final insertion sort is O(N^2)