1 bubble sort

1. The data to be sorted can be in array or linked list
2. Exchange only when strictly unequal, that is, when equal, do not exchange, which shows that the algorithm is stable

Pseudo code

void Bubble_Sort(ElementType A[], int N)
{
	for (p = N - 1; p > 0; p--)
	{
		flag = 0;
		for (i = 0; i < p; i++)
		{
			if (A[i] > A[i-1])
			{
				swap(A[i] , A[i-1]);
				flag = 1;
			}
		}
		if (flag == 0)
			break;
	}
}

principle

The first number is compared with the second number. If the first number is large, the position is exchanged. Then compare the second with the third, and so on. After the first round, the maximum value was placed last

code implementation

#include<stdio.h>
int main()
{
	int i,*pointer;
	void swap(int m, int n);
	void pailie(int A[], int N);
	int arr[8] = { 2,1,6,7,8,9,1,1 };
	pailie(arr,8);
	for (i = 0; i < 8; i++)
	{
		printf("%d", arr[i]);
	}
	return 0;
}
void pailie(int *p_1, int N)
{
	int flag;
	int i,p;
	void swap(int m, int n);
	for (p = N - 1; p > 0; p--)
	{
		flag = 0;
		for (i = 0; i < p; i++)
		{
			if (*(p_1+i) > *(p_1+i+1))
			{
				swap(p_1 + i, p_1 + i + 1);
				flag = 1;
			}
		}
		if (flag == 0)
			break;
	}
}
void swap(int *m, int *n)
{
	int temp;
	temp = *m;
	*m = *n;
	*n = temp;
}

11126789

Complexity O(n),O(n square)

2 insert sort

Pseudo code

void Insertion_Sort(ElementType A[], int N)
{
	for (p = 1; p < N; p++)
	{
		tmp =A[p];
		for (i = p; i > 0 && A[i-1] > tmp; i--)
		A[i]=A[i-1];	
	A[i] = tmp;
	}
}

principle

For example, I'm playing cards now. Every time I get a card, I have to arrange the cards from small to large; I now have 3 cards, 2, 6 and 4 respectively; These three have been arranged in order. Then I took another 5 and compared it from the right. I found that 6 was greater than 5, so I put 6 on the fourth and compared it with the second 4. 5 is greater than 4, so the new card 5 is placed.

code implementation

#include<stdio.h>
int main()
{
	void paicu_2(int* pointer, int N);
	int i;
	int arr[8] = { 1,9,5,4,5,6,7,9 };
	paicu_2(arr, 8);
	for (i = 0; i < 8; i++)
	{
		printf("%d", arr[i]);
	}
	return 0;
}

void paicu_2(int *pointer, int N)
{
	int tmp,p,i;
	for (p = 1; p < N; p++)
	{
		tmp = *(pointer+p);
		for (i = p; i > 0 && *(pointer + i-1) > tmp; i--)
			*(pointer + i) = *(pointer + i-1);
		*(pointer + i ) = tmp;
	}
}

14556799

Complexity: O(n) in the right order and O (square of n) in the reverse order
The insertion sorting algorithm is also stable, because the position is changed only when it is absolutely unequal.

3 time complexity next session

• Reverse order pair
  Similar to the concept of linear algebra, here is to say that if I > J, a [i] < a [J], it means that (i,j) is a reverse order pair.
  Because the total number of reverse order pairs of each group of data remains unchanged, the number of algorithms that sort by eliminating one reverse order pair at a time is the same.
  Bubble sort and insert sort exchange one reverse pair at a time
• Insert sort complexity
  O(N+I),N is the number of initial elements, and I is the number of pairs in reverse order;
• The inverse pairs of any N different elements have an average of N(N-1)/4 inverse pairs. The average complexity of any algorithm that only sorts two elements in reverse order of exchange is Ω \Omega Ω (N square). Ω \Omega Ω represents the next term, O represents the upper bound, Θ \Theta Θ Indicates the next and upper bounds

4 Hill sort

The bubble sort and insert sort above only exchange one reverse order pair at a time, so the efficiency is low. In order to improve efficiency, you can exchange methods with others

• Define incremental sequence, for example, 5, 3, 1; Sort each number by interval, which means sorting by 5-interval first, then sorting by 3-interval, and finally sorting by 1-interval.
  Examples are as follows
  

Pseudo code

void Shell_sort(int A[], int N)
	{
		for (D = N / 2; D > 0; D = D / 2 )
		{
			for (p = D; p < N; p++)
			{
				tmp =A[p];
				for (i = p; i > 0 && A[i-D] > tmp; i -= D)
				{
					A[i]=A[i-D];
				}
				A[i]= tmp;
			}
		}
	}

code implementation

#include<stdio.h>
int count=0;
int main()
{
	void paixu_3(int* point, int N);
	int i;
	int arr[8] = { 1,9,6,4,5,6,7,9};
	paixu_3(arr, 8);
	for (i = 0; i < 8; i++)
	{
		printf("%d", arr[i]);
	}
	printf("\n%d",count);
	return 0;
}

void paixu_3(int* point, int N)
{
	int p, D, tmp, i;
	for (D = N / 2; D > 0; D=D/2)
	{
		for (p = D; p < N; p++)
		{
			tmp = *(point + p);
			for (i = p; i > 0 && *(point + i - D) > tmp; i -= D)
			{
				*(point + i) = *(point + i - D);
				count++;
			}

			*(point + i) = tmp;
		}
	}
}

14566799
4

Hibbard sequence

For the most basic incremental series above, the complexity may be Θ \Theta Θ (n square) represents the next and upper bounds, because the incremental elements are not coprime, for example, 8, 4, 2, 1; If so, there may be small increments that don't work at all

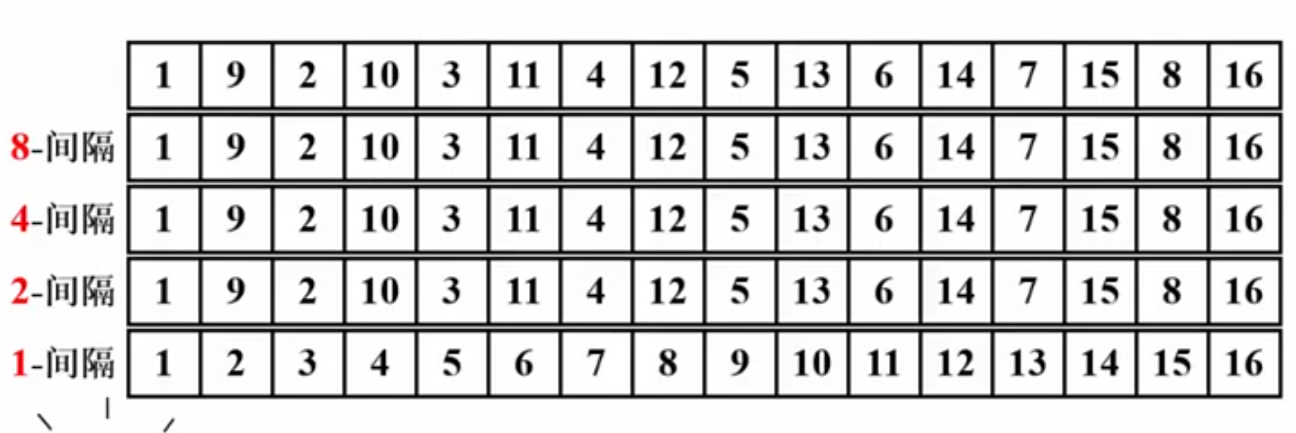
In order to overcome this problem, Hibbard sequence is proposed

5 select sort

Selective sorting principle

• Find the smallest element in the unordered part of the array and put it in the last position of the ordered part

Pseudo code

void Selection_Sort(ElementType A[],int N)
{
	for(i=0;i<N;i++)
	{
		MinPosition=ScanFormin(A,i,N-1);
		Swap(A[i],A[Minposition]);
	}
}

code implementation

#include<stdio.h>
int main()
{
	void Selection_Sort(int* p1, int N);
	int A[20] = { 5,8,7,9,4,5,6,3,15,15,66,48,41,15,16,11,5,1,9,20 };
	Selection_Sort(A, 20);
	for(int i=0;i<20;i++)
		printf("%3d",A[i]);
	return 0;
}
void Selection_Sort(int *p1, int N)
{
	void swap(int* m, int* n);
	int i,MinPosition;
	void ScanForMin(int* p2, int k, int end_num);
	for (i = 0; i < N; i++)
	{
		ScanForMin(p1, i, N - 1);
		swap((p1+i), (p1+N-1));
	}
		
}
void ScanForMin(int *p2, int k, int end_num)//Bubble algorithm for minimum
{
	int i;
	void swap(int* m, int* n);
	for (int i = k; i <= end_num; i++)
		if (*(p2+i) < *(p2 + i + 1))
			swap((p2 + i), (p2 + i + 1));
}
void swap(int *m, int *n)
{
	int temp;
	temp = *m;
	*m = *n;
	*n = temp;
}

  1  3  4  5  5  5  6  7  8  9  9 11 15 15 15 16 20 41 48 66

• The method used to extract the minimum value of the disordered part is bubble sorting. If it is not found, first bubble to find the minimum value of the disordered part, and then put it in the end of the order. It seems to be more complicated. Ha, the following is a good method to find the smallest element without part, the largest heap, the smallest heap

6 heap sort

Find the smallest element, the largest element

Heap sorting basic program (creation, insertion and deletion of heap)

The abstract data structure heap is a heap built for a complete binary tree based on the set of data objects.
Heap is a special binary tree. The largest heap is a complete binary tree whose node elements are greater than all the elements of the left and right sons
Basic idea: insert the tree into the tree according to the order of the array elements, then adjust the nodes of the tree to complete the establishment of the largest and smallest self. The sorting is completed by taking out (deleting) the largest node each time.
==Complexity is linear complexity==

typedef struct HNode *Heap; /* Type definition of heap */
struct HNode {
    ElementType *Data; /* An array of storage elements */
    int Size;          /* Number of current elements in the heap */
    int Capacity;      /* Maximum capacity of the heap */
};
typedef Heap MaxHeap; /* Maximum heap */
typedef Heap MinHeap; /* Minimum heap */

#define MAXDATA 1000 / * the value should be defined as greater than all possible elements in the heap according to the specific situation*/

MaxHeap CreateHeap( int MaxSize )
{ /* Create an empty maximum heap with a capacity of MaxSize */

    MaxHeap H = (MaxHeap)malloc(sizeof(struct HNode));
    H->Data = (ElementType *)malloc((MaxSize+1)*sizeof(ElementType));
    H->Size = 0;
    H->Capacity = MaxSize;
    H->Data[0] = MAXDATA; /* Define sentinel as a value greater than all possible elements in the heap*/

    return H;
}

bool IsFull( MaxHeap H )
{
    return (H->Size == H->Capacity);
}

bool Insert( MaxHeap H, ElementType X )
{ /* Insert element X into maximum heap h, where H - > data [0] has been defined as sentinel */
    int i;
 
    if ( IsFull(H) ) { 
        printf("Maximum heap full");
        return false;
    }
    i = ++H->Size; /* i Points to the position of the last element in the heap after insertion */
    for ( ; H->Data[i/2] < X; i/=2 )
        H->Data[i] = H->Data[i/2]; /* Upper X filter */
    H->Data[i] = X; /* Insert X into */
    return true;
}

#define ERROR -1 / * the error ID should be defined as an element value that cannot appear in the heap according to the specific situation*/

bool IsEmpty( MaxHeap H )
{
    return (H->Size == 0);
}

ElementType DeleteMax( MaxHeap H )
{ /* Extract the element with the largest key value from the maximum heap H and delete a node */
    int Parent, Child;
    ElementType MaxItem, X;

    if ( IsEmpty(H) ) {
        printf("Maximum heap is empty");
        return ERROR;
    }

    MaxItem = H->Data[1]; /* Get the maximum value stored in the root node */
    /* Use the last element in the maximum heap to filter the lower nodes from the root node upward */
    X = H->Data[H->Size--]; /* Note that the size of the current heap should be reduced */
    for( Parent=1; Parent*2<=H->Size; Parent=Child ) {
        Child = Parent * 2;
        if( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) )
            Child++;  /* Child Point to the larger of the left and right child nodes */
        if( X >= H->Data[Child] ) break; /* Found the right place */
        else  /* Lower filter X */
            H->Data[Parent] = H->Data[Child];
    }
    H->Data[Parent] = X;

    return MaxItem;
} 

/*----------- Build maximum reactor-----------*/
void PercDown( MaxHeap H, int p )
{ /* Filter down: adjust the sub heap with H - > data [P] as the root in H to the maximum heap */
    int Parent, Child;
    ElementType X;

    X = H->Data[p]; /* Get the value stored in the root node */
    for( Parent=p; Parent*2<=H->Size; Parent=Child ) {
        Child = Parent * 2;
        if( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) )
            Child++;  /* Child Point to the larger of the left and right child nodes */
        if( X >= H->Data[Child] ) break; /* Found the right place */
        else  /* Lower filter X */
            H->Data[Parent] = H->Data[Child];
    }
    H->Data[Parent] = X;
}

void BuildHeap( MaxHeap H )
{ /* Adjust the elements in H - > data [] to meet the order of the maximum heap  */
  /* It is assumed that all H - > size elements already exist in H - > data [] */

    int i;

    /* Start from the parent node of the last node to the root node 1 */
    for( i = H->Size/2; i>0; i-- )
        PercDown( H, i );
}

Heap sorting algorithm 1 (core program)

void Heap_Sort (ElementType A[],int N)
{
	BuildHeap(A);//Establish minimum heap
	for(i=0;i<N;i++)
		TmpA[i]=DeleteMin(A);
	for(i=0;i<N;i++)
		A[i]=Temp[i];
}

Heap sorting algorithm 1 code example

#include<stdio.h>
#include<stdbool.h>
#define ERROR -1 / * the error ID should be defined as an element value that cannot appear in the heap according to the specific situation*/
typedef struct HNode* Heap; //Pointer to structure (heap)
struct HNode//The binary tree represented by an array represents the heap
{
    int* Data; /* An array of storage elements */
    int Size;          /* Number of current elements in the heap */
    int Capacity;      /* Maximum capacity of the heap */
};
typedef Heap MaxHeap; /* Maximum heap */

#define MAXDATA 1000 / * the value should be defined as greater than all possible elements in the heap according to the specific situation*/

//Create an empty heap with MAXSize capacity
MaxHeap CreateHeap(int MaxSize)    
{ 

    MaxHeap H = (MaxHeap)malloc(sizeof(struct HNode));//H refers to the first address of the storage unit
    H->Data = (int*)malloc((MaxSize) * sizeof(int));
    H->Size = 0;
    H->Capacity = MaxSize;
    H->Data[0] = MAXDATA; /* Define sentinel as a value greater than all possible elements in the heap*/

    return H;
}

bool IsFull(MaxHeap H)
{
    return (H->Size == H->Capacity);
}

void Insert(MaxHeap H, int X)
{ /* Insert element X into maximum heap h, where H - > data [0] has been defined as sentinel */
    int i;

    if (IsFull(H)) {
        printf("Maximum heap full");
    }
    i = ++H->Size; /* i Points to the position of the last element in the heap after insertion */
    for (; H->Data[i / 2] < X; i /= 2)
        H->Data[i] = H->Data[i / 2]; /* Upper filter X */
    H->Data[i] = X; /* Insert X into */
}



bool IsEmpty(MaxHeap H)
{
    return (H->Size == 0);
}

int DeleteMax(MaxHeap H)
{ /* Extract the element with the largest key value from the maximum heap H and delete a node */
    int Parent, Child;
    int MaxItem, X;

    if (IsEmpty(H)) {
        printf("Maximum heap is empty");
        return ERROR;
    }
    MaxItem = H->Data[1]; /* Get the maximum value stored in the root node */
    /* Use the last element in the maximum heap to filter the lower nodes from the root node upward */
    X = H->Data[H->Size--]; /* Note that the size of the current heap should be reduced */
    for (Parent = 1; Parent * 2 <= H->Size; Parent = Child) {
        Child = Parent * 2;
        if ((Child != H->Size) && (H->Data[Child] < H->Data[Child + 1]))
            Child++;  /* Child Point to the larger of the left and right child nodes */
        if (X >= H->Data[Child]) break; /* Found the right place */
        else  /* Lower filter X */
            H->Data[Parent] = H->Data[Child];
    }
    H->Data[Parent] = X;

    return MaxItem;
}

/*----------- Build maximum reactor-----------*/
void PercDown(MaxHeap H, int p)
{ /* Filter down: adjust the sub heap with H - > data [P] as the root in H to the maximum heap */
    int Parent, Child;
    int X;

    X = H->Data[p]; /* Get the value stored in the root node */
    for (Parent = p; Parent * 2 <= H->Size; Parent = Child) {
        Child = Parent * 2;
        if ((Child != H->Size) && (H->Data[Child] < H->Data[Child + 1]))
            Child++;  /* Child Point to the larger of the left and right child nodes */
        if (X >= H->Data[Child]) break; /* Found the right place */
        else  /* Lower filter X */
            H->Data[Parent] = H->Data[Child];
    }
    H->Data[Parent] = X;
}

void BuildHeap(MaxHeap H)//H is the structure pointer variable
{ /* Adjust the elements in H - > data [] to meet the order of the maximum heap  */
  /* It is assumed that all H - > size elements already exist in H - > data [] */

    int i;

    /* Start from the parent node of the last node to the root node 1 */
    for (i = H->Size / 2; i > 0; i--)
        PercDown(H, i);
}


void paixu_heap(int *A, int N)
{
    int i;
    MaxHeap H_1;
    int TmpA[16];
    H_1 = CreateHeap(16);
    for (i =1; i < 16; i++)
    {
        Insert(H_1, *(A+i));
    }
    BuildHeap(H_1);
    for (i = 1; i < N; i++)
    	A[i] = DeleteMax(H_1);
  //    TmpA[i] = DeleteMax(H_1);
  //for (i = 0; i < N; i++)
  //    A[i] = TmpA[i];
}

int main()
{
    int arr[16] = { MAXDATA,1, 6, 8, 4, 8, 9, 1, 12, 66, 78, 12, 1, 6, 9, 5 };
    paixu_heap(arr, 16);
    for (int i = 1; i < 16; i++)
    {
        printf("%d  ", arr[i]);
    }
    return 0;
}

78  66  12  12  9  9  8  8  6  6  5  4  1  1  1

7 merging of ordered subsequences

Merging algorithm

Unified function interface