1) Insert

Direct insertion sort

thinking
When inserting the first i(i>=1) element, the preceding array[0],array[1],..., array[i-1] is already sorted, and the sort order of array[i] is compared with that of array[i-1],array[i-2],.... The insertion position is to insert array[i], the order of elements on the original position is moved backwards.

Characteristic

1. The closer the elements are to order, the more efficient the direct insertion sort algorithm is
2. Time Complexity: O(N^2)
3. Spatial Complexity: O(1), which is a stable sorting algorithm
4. Stability: Stability

The code is as follows

void InsertSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				//Without a[end]=tmp added here, it would not be the idea of inserting sort
				end--;
			}
			else
			{
				break;
			}
			a[end + 1] = tmp;
            //Note that don't write here to insert sort ideas for tmp=a[end + 1] Comb and rewrite code clearly
		}
	}
}

Hill Sort

thinking
The basic idea of Hill sorting is to first select an integer, divide all records in the file to be sorted into groups, and then sort the records in each group. Then, take and repeat the grouping and sorting. When = 1 is reached, all records are sorted in a unified group.

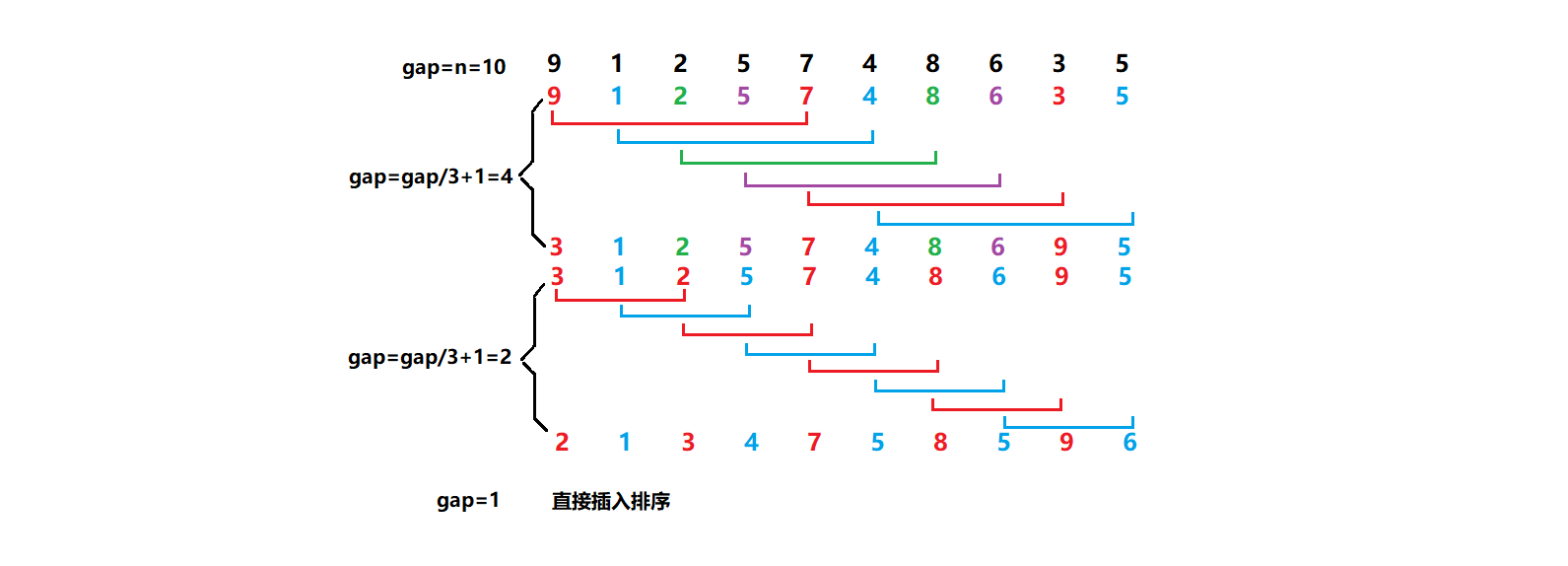
Characteristic

1. Hill sort is an optimization of direct insert sort
2. When gap > 1, they are all pre-sorted in order to make the arrays closer to order. When gap == 1, the arrays are close to order, which is faster. As a whole, optimization can be achieved. Performance tests can be compared after implementation.
3. The time complexity of Hill sorting is not easy to compute because there are many gap s that make it difficult to compute, so the time complexity of Hill sorting given in several trees is not fixed (generally equal to O(N^1.3)).
4. Stability: Unstable

The code is as follows: (tested gap = gap / 3 + 1 is slightly faster, gap=gap/2 is also possible)

// Shell Sort
void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		//gap=gap/2;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end = end - gap;
				}
				else
				{
					break;
				}
				a[end + gap] = tmp;
			}
		}
	}	
}

2) Selection

1. Select Sort

thinking
Each time the smallest (or largest) element is selected from the data elements to be sorted, and stored at the beginning of the sequence, begin adds one and end minus one. As long as begin is less than the end, the operation is cycled until all the data elements to be sorted are finished.
Characteristic

1. Direct Selection Sort Thinking is very understandable, but not very efficient. It is rarely used in practice
2. Time Complexity: O(N^2)
3. Spatial Complexity: O(1)
4. Stability: Unstable

The code is as follows

// Select Sort
void SelectSort(int* a, int n)
{
	int begin = 0;
	int end = n - 1;
	int mini, maxi = begin;
	while (begin < end)
	{
		mini = begin;
		maxi = begin;
		for (int i = begin; i <= end; i++)
		{
			if (a[i] > a[maxi])
			{
				maxi = i;
			}
			if (a[i] < a[mini])
			{
				mini = i;
			}
		}
		if (maxi == begin)
		//if the maximum value is begin, then after the minimum is swapped, the maxi recorded by the maximum value is not begin > but on the mini. So add one and only ifjudgment is required
		{
			int tmp = a[begin];
			a[begin] = a[mini];
			a[mini] = tmp;
			tmp = a[end];
			a[end] = a[mini];
			a[mini] = tmp;
		}
		else
		{
			int tmp = a[begin];
			a[begin] = a[mini];
			a[mini] = tmp;
			tmp = a[end];
			a[end] = a[maxi];
			a[maxi] = tmp;
		}
		++begin;
		--end;
	}
}

(2) Heap sorting

Ideas: Data Structure--Heap Application in Binary Tree (Initial) ->Heap Sorting

Characteristic

1. Heap sorting uses heaps to select numbers, which is much more efficient
2. Time complexity: O(N*logN)
3. Spatial Complexity: O(1)
4. Stability: Unstable

The code is as follows

// Heap Sorting
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child<n)
	{
		if (child<n-1 && a[child] < a[child + 1])//Child <n-1 prevents crossing borders
		{
			child = child + 1;
		}
		if (a[child] > a[parent])
		{
			int tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}
void HeapSort(int* a, int n)
{
	for (int i = ((n - 1) - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	int end = n - 1;
	while(end>0)
	{
		int tmp = a[end];
		a[end] = a[0];
		a[0] = tmp;
		end--;
		AdjustDown(a, end + 1, 0);
	}
}

3) Exchange

1. Bubble sort

Ideas: Bubble sort of algorithm (optimization)

Characteristic

1. Bubble sort is a very easy to understand sort
2. Time Complexity: O(N^2)
3. Spatial Complexity: O(1)
4. Stability: Stability

(2) Quick sorting

I: Recursive (all three) (you need to find a key value first)

1. hoare version (initial version)

Ideas:
The leftmost is the key, so go left first and look for bigger than the key, right then look for smaller than the key, find and stop swapping until you meet left and right
Right most key and vice versa
Below is a key image on the right (pictures collected over the Internet)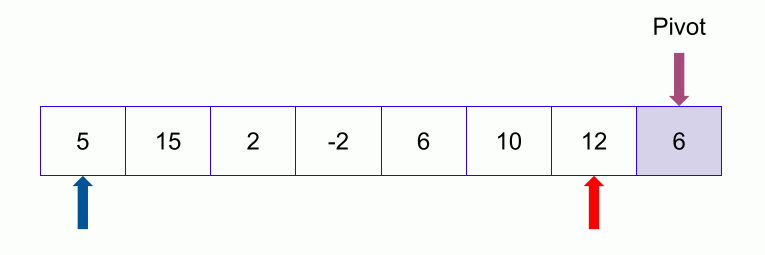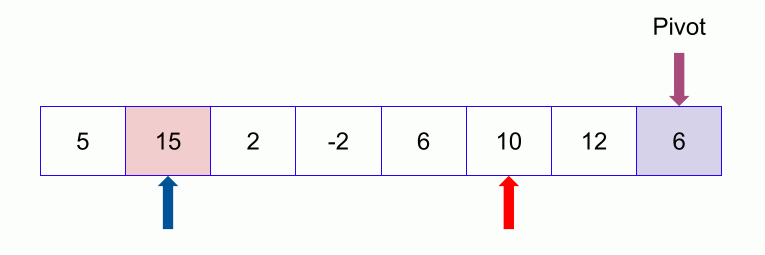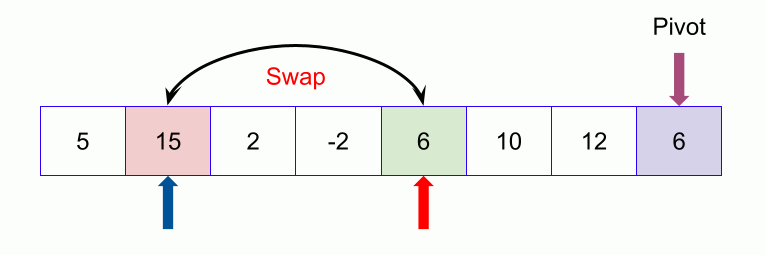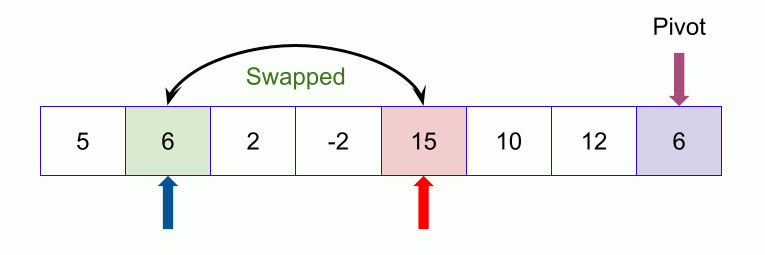
The code is as follows:

// Quick Sort hoare Versions
void PartSort1(int* a, int left, int right)
{
	int Right = right;
	if (right - left <= 1)
		return;
	///Triple selection optimization section
	int tmpK = FindTheKey(a, left, right);//Triple-Number Selection for key Recorded with tmpK
	int tmp = a[left];
	a[left] = a[tmpK];
	a[tmpK] = tmp;//Remember to swap the guaranteed key at the leftmost (keep the key at left)
	///Triple selection optimization section
	int keyi = left;
	int key = a[keyi];//Record key
	while (left < right)
	{
		//Find Small on Right
		while (a[right] >= key && left < right)//Contains the equal case
		{
			right--;
		}
		//Find Big on Left
		while (a[left] <= key && left < right)
		{
			left++;
		}
		tmp = a[left];
		a[left] = a[right];
		a[right] = tmp;
	}
	tmp = a[left];//left right meets, left==right
	a[left] = a[keyi];
	a[keyi] = tmp;
	PartSort1(a, 0, keyi - 1);
	PartSort1(a, keyi + 1, Right);
}

1. pavement thickness measurement by trench excavation

Ideas:

1. Like the first method, the first one is to find the key (the number taken out by the middle of three numbers) and the leftmost (the rightmost can also be)
2. Record key
3. Keys are marked as Keyi
4. Start right and fill the pit when you find it. The Keyi is updated to right. When rightstops, the left starts to look big to the right and the Keyi is updated to left.
5. Until left and right meet, right==left, then add the key that was first recorded to the pit

The code is as follows:

}
// Quick Sort Digging
void PartSort2(int* a, int left, int right)
{
	int Right = right;
	if (right - left <= 1)
		return;

	int tmpK= FindTheKey(a, left, right);//tmpK Record for Finding Pits by Three-Number Selection
	int tmp = a[left];
	a[left] = a[tmpK];
	a[tmpK] = tmp;//Remember to swap (put pit first)

	int kengi = left;
	int key = a[kengi];//Record key
	while (left < right)
	{
		//Find small, fill hole on right
		while (a[right] >= key && left < right)//Include equal cases????
		{
			right--;
		}
		
		a[kengi] = a[right];
		kengi = right;
		//Look for a big hole on the left
		while (a[left] <= key && left < right)
		{
			left++;
		}
		
		a[kengi] = a[left];
		kengi = left;
	}
	a[kengi] = key;//Fill in the record key at the end
	PartSort2(a, 0, kengi - 1);
	PartSort2(a, kengi+1, Right);
}

1. Front and back pointer versions (key differs slightly between left and right)

Ideas (key on left):

1. prev subscript 0, cur subscript 1 begins
2. cur goes forward and finds data smaller than key
3. When you find this key's small data, stop, ++ prev
4. Swap values of prev and cur pointing to position until cur reaches the end of the array
5. Exchange last prev position with key

Ideas (key differentiates right from left):

1. prev starts at subscript-1 and cur at subscript 0
2. cur encounters a key stop, at which point prev has to exchange ++ with the key

Be careful

1. Before cur encounters a value larger than key, prev must follow cur
2. When cur encounters a value larger than key, there is a greater interval between prev and cur than key

Optimize:
So optimization adds a [++ prev] when if a [cur] < a [keyi]!=A[cur] Avoid redundant interchanges when prev follows cur

The code is as follows (key on the left)

// Quick Sort Back and Front Pointer Method (keyi at leftmost)
void PartSort3_left(int* a, int left, int right)
{
	int keyi = left;
	int prev = left;
	int cur = prev + 1;
	if (cur > right)
		return;
	while (cur <= right)
	{
		if (a[cur] < a[keyi]&&a[++prev]!=a[cur])
		//a[++prev]!=a[cur] is optimized If cur has always been found smaller than a[keyi], prev++ will be the same as cur every time, so there will be a lot of swaps within if
		{
			int tmp = a[prev];
			a[prev] = a[cur];
			a[cur] = tmp;
		}
		cur++;
	}
	int tmp = a[keyi];
	a[keyi] = a[prev];
	a[prev] = tmp;
	PartSort3_left(a, 0, prev-1);
	PartSort3_left(a, prev+1, right);
}

The code is as follows (key on the right)

// Quick sort before and after pointer method (keyi is on the right-most side)
void PartSort3_right(int* a, int left, int right)
{
	int keyi = right;
	int prev = left-1;
	int cur = left;
	if (cur > keyi-1)
		return;
	while (cur < keyi)
	{
		if (a[cur] < a[keyi] && a[++prev] != a[cur])
		//a[++prev]!=a[cur] is an optimization of redundant exchange If cur has always been found to be smaller than a[keyi], prev++ will be the same as cur every time, so that the exchange within if will be much redundant
		{
			int tmp = a[prev];
			a[prev] = a[cur];
			a[cur] = tmp;
		}
		cur++;
	}
	prev++;
	int tmp = a[keyi];
	a[keyi] = a[prev];
	a[prev] = tmp;
	PartSort3_right(a, 0, prev - 1);
	PartSort3_right(a, prev + 1, right);
}

II: Non-recursive

Recursion versus loop iteration:

1. Recursion too deep, causing stack overflow
2. Performance issues (Compiler optimizations are getting better and less important now)

There are two general types of recursive to non-recursive writing:

1. Direct loop iteration
2. Stack+Loop Iteration

Non-recursive quick queue ideas:

1. Build a stack
2. Because in recursion we use key s as the middle every time, we recursively operate on both sides as an array
3. The first time you put it on the stack, press in the first subscript of the array (first press the tail, then the head), and write it as begin end.
4. Enter the loop As long as the stack is not empty, continue to call the fast-paced function (single-pass version is not recursive). For example, before and after the pointer version, each time the prev position is reached, the new key is located
5. To determine whether the left side of prev (begin is less than prev-1) and the right side (prev+1 is less than end) of prev are valid, continue stacking with two new arrays (end first, end first)
6. Until there is only one number cut-off on the left and right sides of the prev

Be careful:

1. pop stack after each top fetch
   

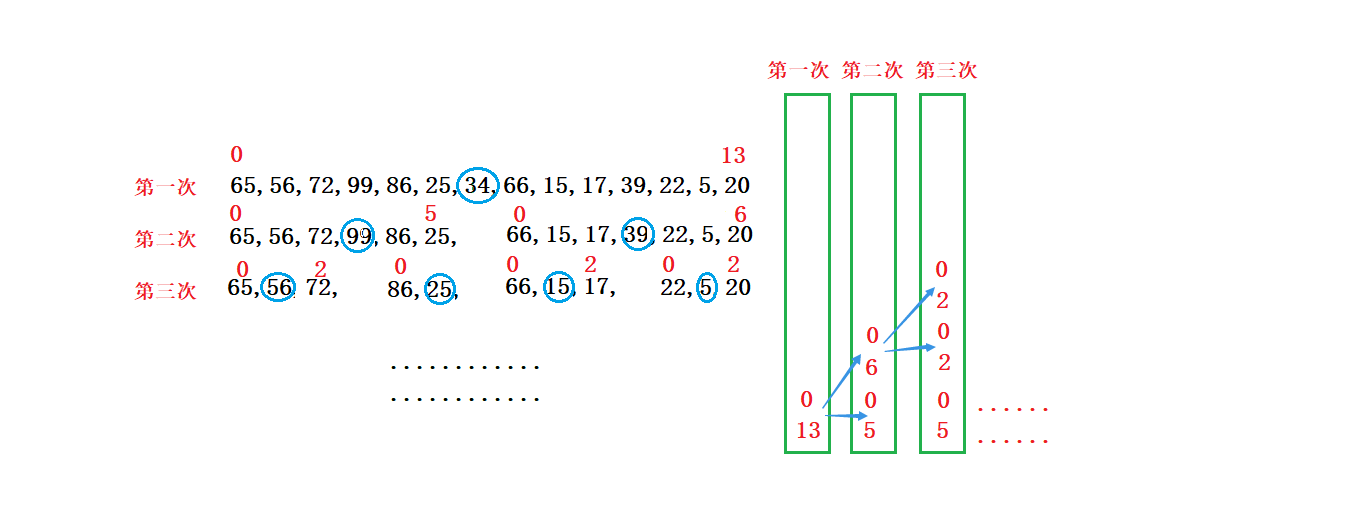
The code is as follows:

// Quick sort before and after pointer method (stack + iteration loop key on left)
void Stack_While_PartSort3_left(int* a, int left, int right)
{
	ST st;
	StackInit(&st);
	StackPush(&st, right);
	StackPush(&st, left);
	while (!StackEmpty(&st))
	{
		int begin= StackTop(&st);
		StackPop(&st);
		int end= StackTop(&st);
		StackPop(&st);
		//Quick Row Functions Invoked (Single Edition No Recursion)
		//PartSort1(int* a, int left, int right)
		//PartSort2(int* a, int left, int right)
		//PartSort3_left(int* a, int left, int right)
		//Quick Row Functions Invoked (Single Edition No Recursion)
		//keyi = prev;
		if (prev - 1 > begin)
		{
			StackPush(&st, prev-1);
			StackPush(&st, begin);
		}
		if (prev + 1 < end)
		{
			StackPush(&st, end);
			StackPush(&st, prev + 1);
		}
	}
}

III: Three-digit selection (optimization of key selection)

thinking
Select the first, middle and last three positions of the array, and select the middle value to return the subscript

The code is as follows:

//Middle of Three Numbers
int FindTheKey(int *a, int left, int right)
{
	unsigned int mid = left + (right - left) / 2;//To prevent left+right overflow int from overflowing with int mid = (left+right)/2 or mid = > (begin + end) > 1;
	if (a[left] > a[mid])
	{
		if (a[right] < a[mid])
			return mid;
		else if (a[right] > a[left])
			return left;
		else
			return right;
	}
	else // a[left] < a[mid]
	{
		if (a[right] > a[mid])
			return mid;
		else if (a[right] < a[left])
			return left;
		else
			return right;
	}
}

Fast row characteristics:

1. Quick Sorting is called Quick Sorting because its overall performance and usage scenarios are good.
2. Time complexity: O(N*logN)
3. Spatial Complexity: O(logN)
4. Stability: Unstable

4) Merger

1. Merge and Sort

I: Recursive Version

Ideas:
This algorithm is a very typical application of Divide and Conquer. Merging existing ordered subsequences results in a completely ordered sequence; that is, ordering each subsequence before ordering subsequence segments. Merging two ordered tables into one ordered table is called two-way merge. The following figure shows the result.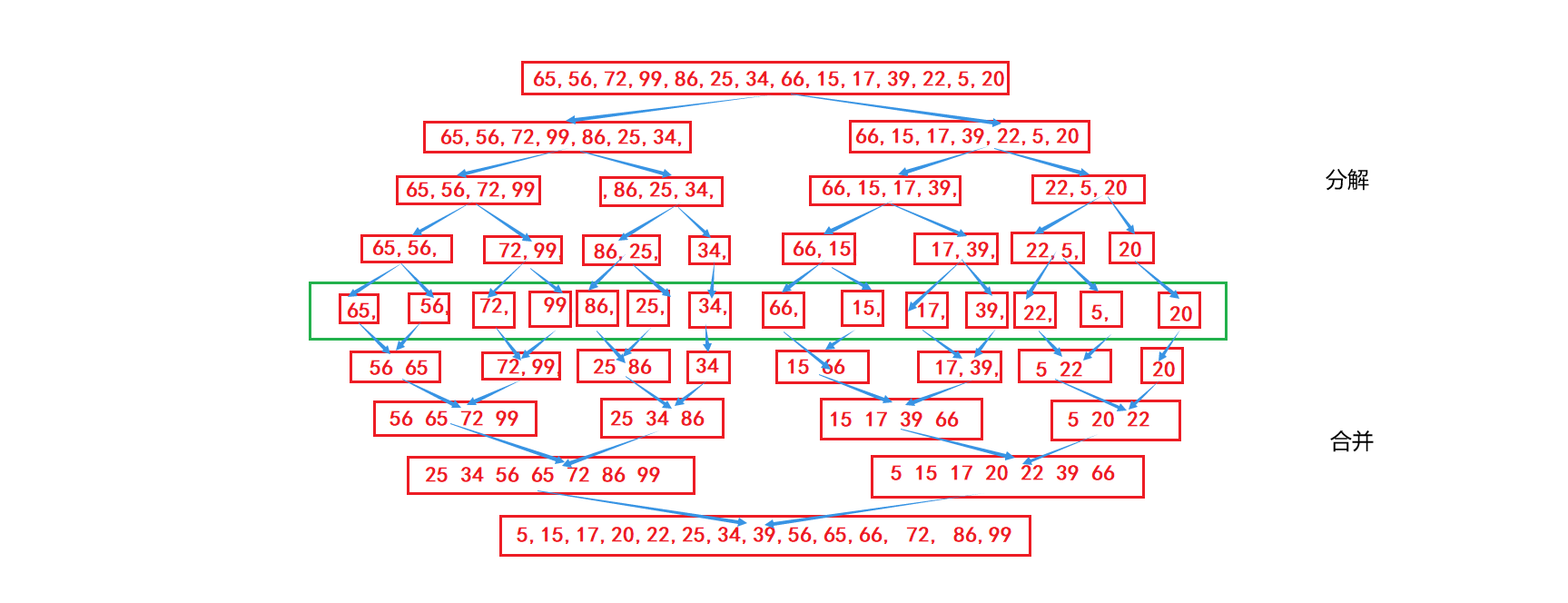
Characteristic:

1. The disadvantage of merging is that it requires the spatial complexity of O(N). The thought of merging and sorting is more to solve the problem of out-of-disk sorting.
2. Time complexity: O(N*logN)
3. Spatial Complexity: O(N)
4. Stability: Stability

The code is as follows

 Recursive implementation of merge sort
void MergeSort(int* a, int n)
{
	int *tmp = (int *)malloc(sizeof(int)*n);//Temporary Array
	_MergeSort(a, tmp, 0, n-1);//right is subscript
	free(tmp);
}
void _MergeSort(int* a, int *tmp, int left, int right)
{
	if (left >= right)
		return;
	int mid = (left + right) / 2;
	_MergeSort(a, tmp,  left, mid);
	_MergeSort(a, tmp, mid+1, right);
	int begin1 = left;
	int end1 = mid;
	int begin2 = mid + 1;
	int end2 = right;
	int tmpi = left;
	while ((begin1 <= end1) && (begin2 <= end2))
	{
		if (a[begin1] < a[begin2])
		{
			tmp[tmpi++] = a[begin1++];
		}
		else
		{
			tmp[tmpi++] = a[begin2++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[tmpi++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[tmpi++] = a[begin2++];
	}
	for (int i = 0; i < tmpi; i++)
	{
		a[i] = tmp[i];
	}
}

II: Non-recursive versions

Here is the reference

5) Non-comparative Sorting

1 Count sorting

Count ordering, also known as the pigeon nest principle, is a distorted application of hash direct addressing.
Ideas:

1. Count occurrences of the same elements (elements are subscripts so all comparisons, exchanges are omitted)
2. Recycle a sequence into its original sequence based on statistical results

Characteristic:

1. Count sorting is efficient in a data range set, but has limited scope and scenarios.
2. Time Complexity: O(MAX(N, Range))
3. Spatial Complexity: O (Range)

The code is as follows

 Count Sort
void CountSort(int* a, int n)
{
	
	int min = a[0];
	int max = a[0];
	for (int i = 1; i < n; i++)
	{
		if (a[i] < min)
			min = a[i];
		if (a[i] > max)
			max = a[i];
	}
	int maxi = max-min;
	int *tmp = calloc(maxi+1, sizeof(int));
	//The first parameter of calloc is the number of openings, so note that subscripts plus one
	int ai = 0;
	for (int i = 0; i < n; i++)
	{
		tmp[a[i] - min]++;
	}
	for (int i = 0; i <=maxi; i++)
	{
		if (tmp[i] != 0)
		{
			while (tmp[i]--)
			{
				a[ai++] = i + min;
			}
		}
	}
}

Analysis: As shown in the code, because the array elements to be sorted may be too large, which wastes a lot of space, we find the minimum number (each element-minimum) as the mapping of this element, and add this minimum number last.
Note: This algorithm is not practical when the difference between the elements of the array to be sorted is too large and only works for specific scenarios

(2) Sort of cardinality

(3) Bucket sorting