Data structure - sorting notes of arrays and generalized tables (Chapter 6). If there are errors, please correct them.
Compressed storage of special matrix
Common body type

• When the number s of non-zero elements in a matrix with large order is very small relative to the total number t of matrix elements, that is, S ≪ \ll ≪ t, the matrix is called sparse matrix.
• There is an obvious difference between sparse matrix and special matrix: the distribution of special elements in special matrix has a certain law, while the distribution of special elements (non-zero elements) in sparse matrix has no law, that is, it has randomness. The description of sparse matrix abstract data type is similar to that of d(d=2) dimensional array abstract data type.

Triple representation of sparse matrix

• The compressed storage method of sparse matrix is to store only non-zero elements. Because the distribution of non-zero elements in sparse matrix has no law, the row subscript, column subscript and element value corresponding to the non-zero element must be stored at the same time. In this way, each non-zero element in the sparse matrix consists of a triple ( i , j , a i , j ) (i,j,a_{i,j}) (i,j,ai,j) uniquely determine that all non-zero elements in the sparse matrix form a triple linear table.

Example: suppose there is a 6 × 7th order sparse matrix A:
A 6 × 7 = [ 0 0 1 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 7 4 ] A_{6×7}=\begin{bmatrix} 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 2 & 0 & 0 & 0 & 0 & 0\\ 3 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 5 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 6 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 7 & 4\\ \end{bmatrix} A6×7​=⎣⎢⎢⎢⎢⎢⎢⎡​003000​020000​100000​000500​000060​000007​000004​⎦⎥⎥⎥⎥⎥⎥⎤​

Then the triples corresponding to sparse matrix A can be expressed as:

In order of behavior:	i i i	j j j	a i , j a_{i,j} ai,j​	Column based order:	i i i	j j j	a i , j a_{i,j} ai,j​
(0,2,1)	0	2	1	(2,0,3)	2	0	3
(1,1,2)	1	1	2	(1,1,2)	1	1	2
(2,0,3)	2	0	3	(0,2,1)	0	2	1
(3,3,5)	3	3	5	(3,3,5)	3	3	5
(4,4,6)	4	4	6	(4,4,6)	4	4	6
(5,5,7)	5	5	7	(5,5,7)	5	5	7
(5,6,4)	5	6	4	(5,6,4)	5	6	4

• If the three tuple linear table of sparse matrix is stored according to the sequential storage structure, it is called the three tuple sequential table of sparse matrix, which is abbreviated as the list of 3-tuples. The data type declaration of the triple sequence table is as follows:

#include<stdio.h>
#Define m < sparse matrix rows >
#Define n < sparse matrix columns >
#Define maxsize < maximum number of non-zero elements in sparse matrix >
typedef int ElemType;
typedef struct
{
	int r; //Line number
	int c; //Column number
	ElemType d; //Element value 
}TupNode; //Triple type

typedef struct
{
	int rows; //Line number
	int cols; //Column number
	int nums; //Number of non-zero elements
	TupNode data[MaxSize];
}TSMatrix; //Type of triplet order table

• Among them, the non-zero elements represented in the data field are usually arranged in row order, that is, a storage structure with subscripts ordered by row.

Create its triplet representation from a two-dimensional sparse matrix

• Scan the two-dimensional sparse matrix A with row order as the main order, and insert the non-zero elements into the triple order table in turn.

void CreateMat(TSMatrix& t, ElemType A[M][N])
{
	t.rows = M;
	t.cols = N;
	t.nums = 0;
	for (int i = 0; i < M; i++)
	{
		for (int j = 0; j < N; j++)
			if (A[i][j] != 0) //Only non-zero elements are stored
			{
				t.data[t.nums].r = i;
				t.data[t.nums].c = j;
				t.data[t.nums].d = A[i][j];
				t.nums++;
			}
	}
}

Assignment of triple elements

• This operation is to perform a [i] [J] = x for sparse matrix A (x is usually a non-zero value). First, find the appropriate position k in the triple order table T. If the position corresponds to a non-zero element, modify its d data field to X; Otherwise, you need to insert a non-zero element, move the elements of k ~ t.num-1 back one position, and then insert the non-zero element x into
  t.data[k].

bool Value(TSMatrix& t, ElemType x, int i, int j)
{
	int k, k1;
	if (i >= t.rows || j >= t.cols) return false; //i. j parameter is out of bounds and returns false
	while (k < t.nums && t.data[k].r < i) k++; //Find the first non-0 element in line i
	while (k < t.nums && t.data[k].r == i && t.data[k].c < j) k++; //Find column j in the non-0 element in row i
	if (t.data[k].r == i && t.data[k].c == j) t.data[k].d = x; //If such a non-0 element exists, modify the value of the non-0 element
	else //If there is no such non-zero element, several elements are moved back one position
	{
		for (k1 = t.nums - 1; k1 >= k; k1--)
		{
			t.data[k1 + 1].r = t.data[k1].r;
			t.data[k1 + 1].c = t.data[k1].c;
			t.data[k1 + 1].d= t.data[k1].d;
		}
		t.data[k].r = i; //Insert non-zero element x
		t.data[k].c = j;
		t.data[k].d = x;
		t.nums++; //The number of non-0 elements increases by 1
	}
	return true; //Return true after successful operation
}

Assigns the element value at the specified position to the variable

• This operation is to execute x=A[i][j] for sparse matrix A, that is, extract the element value of the specified subscript in a. First, find the specified position in the triple order table. If it is found, it indicates that it is a non-zero element, and assign its value to X; Otherwise, it means zero element, set x=0.

bool Assign(TSMatrix& t, ElemType& x, int i, int j)
{
	int k = 0;
	if (i >= t.cols && j >= t.rows) return false;
	while (k < t.nums && t.data[k].r < i) k++;
	while (k < t.nums && t.data[k].r == i && t.data[k].c < j) k++;
	if (t.data[k].r == i && t.data[k].c == j) x = t.data[k].d;
	else x=0;
	return true;
}

Output triplet

• The operation scans the triple sequence table t from beginning to end and outputs the element values in turn.

void DispMat(TSMatrix t)
{
	if (t.nums <= 0) return; //Returns directly when there are no non-zero elements
	printf("\t%d\t%d\t%d\n", t.rows, t.cols, t.nums);
	printf("\t-------------------------\n");
	for (int k = 0; k < t.nums; k++) //Output all non-0 elements
		printf("\t%d\t%d\t%d\n", t.data[k].r, t.data[k].c, t.data[k].d);
}

Transposed triples of sparse matrices

• The operation is for an m × Sparse matrix of n A m × n A_{m×n} Am × n, find its transpose matrix A n × m A_{n×m} An × m, i.e b i , j = a j , i b_{i,j}=a_{j,i} bi,j = aj,i, where 0 ≤ i ≤ m − 1 ， 0 ≤ j ≤ n − 1 0≤i≤m-1，0≤j≤n-1 0≤i≤m−1，0≤j≤n−1. The algorithm idea adopted is that the triplet sequence table corresponding to A is t, and the triplet sequence table corresponding to transpose matrix B is tb. Press v=0,1,..., t.cols to find the element with column number V in T. for each such element, exchange rows and columns and add it to tb.

void TranTup(TSMatrix& t, TSMatrix& tb)
{
	int k1 = 0; //k1 record the number of elements in tb
	tb.rows = t.rows;
	tb.cols = t.cols;
	tb.nums = t.nums;
	if (t.nums <= 0) return; //Returns directly when there are no non-zero elements
	for (int v = 0; v < t.cols; v++) //When there are non-zero elements, execute transpose, press v=0, 1 t.cols cycle
	{
		for (int k = 0; k < t.nums; k++) //k is used to scan all elements of t.data
			if (t.data[k].c == v) //Found an element with column number v
			{
				tb.data[k1].r = t.data[k].c; //Add rows and columns to tb after exchange
				tb.data[k1].c = t.data[k].r;
				tb.data[k1].d = t.data[k].d;
				k1++; //The number of elements in tb increases by 1
			}
	}
}

• The algorithm contains a double for loop, and its time complexity is O(t.cols) × t.nums). The worst case is when the number of non-zero elements in the sparse matrix is t.num and m × n in the same order of magnitude, the time complexity is O ( m × n 2 ) O(m×n^2) O(m × n2), so this is not an efficient algorithm.

Complete code

#include<stdio.h>
#define M 6
#define N 7
#define MaxSize 42
int A[M][N] = { {0,0,1,0,0,0,0},{0,2,0,0,0,0,0},{3,0,0,0,0,0,0,},
						 {0,0,0,5,0,0,0},{0,0,0,0,6,0,0},{0,0,0,0,0,7,4} };

typedef int ElemType;
typedef struct
{
	int r; //Line number
	int c; //Column number
	ElemType d; //Element value 
}TupNode; //Triple type

typedef struct
{
	int rows; //Line number
	int cols; //Column number
	int nums; //Number of non-zero elements
	TupNode data[MaxSize];
}TSMatrix; //Type of triplet order table

//--------Triple operation---------
void CreateMat(TSMatrix& t, ElemType A[M][N]) //Create its triplet representation from a two-dimensional sparse matrix
{
	t.rows = M;
	t.cols = N;
	t.nums = 0;
	for (int i = 0; i < M; i++)
	{
		for (int j = 0; j < N; j++)
			if (A[i][j] != 0) //Only non-zero elements are stored
			{
				t.data[t.nums].r = i;
				t.data[t.nums].c = j;
				t.data[t.nums].d = A[i][j];
				t.nums++;
			}
	}
} 

bool Value(TSMatrix& t, ElemType x, int i, int j) //Assignment of triple elements
{
	int k=0, k1;
	if (i >= t.rows || j >= t.cols) return false; //i. j parameter is out of bounds and returns false
	while (k < t.nums && t.data[k].r < i) k++; //Find the first non-0 element in line i
	while (k < t.nums && t.data[k].r == i && t.data[k].c < j) k++; //Find column j in the non-0 element in row i
	if (t.data[k].r == i && t.data[k].c == j) t.data[k].d = x; //If such a non-0 element exists, modify the value of the non-0 element
	else //If there is no such non-zero element, several elements are moved back one position
	{
		for (k1 = t.nums - 1; k1 >= k; k1--)
		{
			t.data[k1 + 1].r = t.data[k1].r;
			t.data[k1 + 1].c = t.data[k1].c;
			t.data[k1 + 1].d= t.data[k1].d;
		}
		t.data[k].r = i; //Insert non-zero element x
		t.data[k].c = j;
		t.data[k].d = x;
		t.nums++; //The number of non-0 elements increases by 1
	}
	return true; //Return true after successful operation
}

bool Assign(TSMatrix& t, ElemType& x, int i, int j) //Assigns the element value at the specified position to the variable
{
	int k = 0;
	if (i >= t.cols && j >= t.rows) return false;
	while (k < t.nums && t.data[k].r < i) k++;
	while (k < t.nums && t.data[k].r == i && t.data[k].c < j) k++;
	if (t.data[k].r == i && t.data[k].c == j) x = t.data[k].d;
	else x=0;
	return true;
}

void DispTup(TSMatrix t) //Output triplet
{
	if (t.nums <= 0) return; //Returns directly when there are no non-zero elements
	printf("\t%d\t%d\t%d\n", t.rows, t.cols, t.nums);
	printf("\t------------------\n");
	for (int k = 0; k < t.nums; k++) //Output all non-0 elements
		printf("\t%d\t%d\t%d\n", t.data[k].r, t.data[k].c, t.data[k].d);
}

void TranTup(TSMatrix& t, TSMatrix& tb) //Transposed triples of sparse matrices
{
	int k1 = 0; //k1 record the number of elements in tb
	tb.rows = t.rows;
	tb.cols = t.cols;
	tb.nums = t.nums;
	if (t.nums <= 0) return; //Returns directly when there are no non-zero elements
	for (int v = 0; v < t.cols; v++) //When there are non-zero elements, execute transpose, press v=0, 1 t.cols cycle
	{
		for (int k = 0; k < t.nums; k++) //k is used to scan all elements of t.data
			if (t.data[k].c == v) //Found an element with column number v
			{
				tb.data[k1].r = t.data[k].c; //Add rows and columns to tb after exchange
				tb.data[k1].c = t.data[k].r;
				tb.data[k1].d = t.data[k].d;
				k1++; //The number of elements in tb increases by 1
			}
	}
}

//-----------Matrix operation---------
void DispMat(ElemType A[M][N]) //Output matrix
{
	for (int i = 0; i < M; i++)
	{
		for (int j = 0; j < N; j++)
			printf("\t%d ", A[i][j]);
		printf("\n");
	}
}

void DispTranMat(ElemType B[N][M]) //Transpose of output matrix
{
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < M; j++)
			printf("\t%d ", B[i][j]);
		printf("\n");
	}
}

void TranMat(ElemType B[N][M]) //Matrix transpose
{
	for (int i = 0; i < N; i++)
		for (int j = 0; j < M; j++)
			B[i][j] = A[j][i];
}

void ValueMat(ElemType A[M][N], ElemType x, int i, int j)  //Modify the value of the corresponding position of the matrix
{
	for (int m = 0; m < N; m++)
		for (int n = 0; n < M; n++)
			if (m == i && n == j) A[m][n] = x;
}

int main()
{
	TSMatrix t, tb;
	ElemType B[N][M], x;
	int i, j;
	CreateMat(t,A);
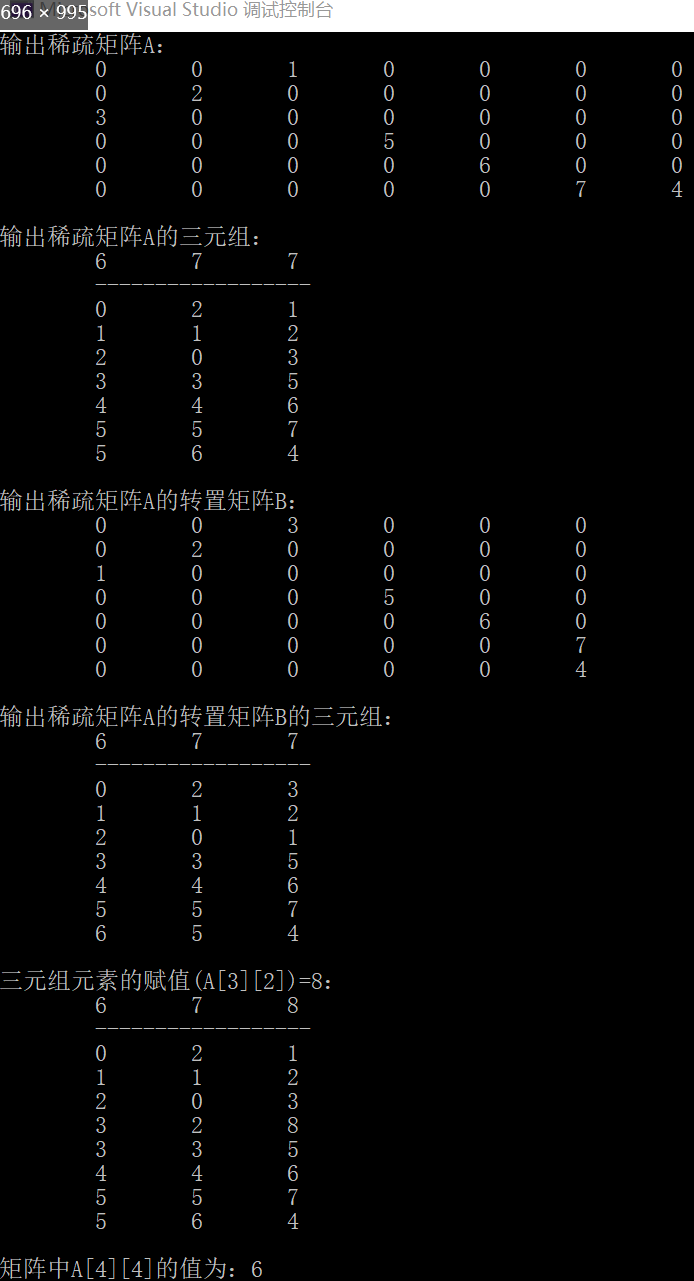
	printf("Output sparse matrix A: \n");
	DispMat(A);
	printf("\n Output sparse matrix A Triples of:\n");
	DispTup(t);
	TranMat(B);
	printf("\n Output sparse matrix A Transposed matrix  B: \n");
	DispTranMat(B);
	TranTup(t, tb);
	printf("\n Output sparse matrix A Transposed matrix  B Triples of:\n");
	DispTup(tb);
	x = 8, i = 3, j = 2;
	printf("\n Assignment of triple elements(A[%d][%d])=%d: \n", i, j, x);
	Value(t, x, i, j);
	DispTup(t);
	i = 4, j = 4;
	Assign(t, x, i, j);
	printf("\n Matrix A[%d][%d]The value of is:%d", i, j, x);
	return 0;
}

Program analysis

• It can be seen from the above that after the sparse matrix is stored in the triple order table, the storage space will be saved to a certain extent when the number of non-zero elements is small. If a two-dimensional array is used to store the sparse matrix directly, it has the characteristics of random access, but it will lose the characteristics of random access after storing it in a triple sequential table.

Cross linked list representation of sparse matrix

• Orthogonal list is a chain storage structure of sparse matrix (accordingly, the previous triple order list is a sequential storage structure of sparse matrix).

Example: suppose there is a 3 × 4th order sparse matrix B:
B 3 × 4 = [ 1 0 0 2 0 0 3 0 0 0 0 4 ] B_{3×4}=\begin{bmatrix} 1 & 0 & 0 & 2\\ 0 & 0 & 3 & 0\\ 0 & 0 & 0 & 4\\ \end{bmatrix} B3×4​=⎣⎡​100​000​030​204​⎦⎤​

• The steps to create a cross linked list of sparse matrix B are as follows:

1. For each non-zero element in the sparse matrix, create a node to store it, including the row number, column number and element value of the element. There are four non-zero elements and four data nodes are created.
2. All nodes in the same row form a circular single linked list with the leading node, and the head node of the single linked list with row number I is hr[i]. There are three rows, corresponding to three circular single linked lists, and the head nodes are hr[0]~hr[2]. hr[i](0 ≤ I ≤ 2) the row pointer of the head node points to the head node of the single linked list with row number I.
3. All nodes in the same column form a circular single linked list with the leading node, and the head node of the single linked list with column number j is hd[j]. There are four columns, corresponding to four circular single linked lists, and the head nodes are hd[0]~hd[3]. hd[j](0 ≤ j ≤ 3) the column pointer of the head node points to the head node of the single linked list with column number j.

• Thus, 3 + 4 = 7 circular single linked lists are created, and the number of head nodes is also 7. In fact, hr[i] and hd[j] can be combined to become h[i], that is, h[i] contains both row pointers and column pointers. h[i](0 ≤ I ≤ 2) the row pointer of the head node points to the first node of the single linked list with row number I, and the column pointer of the h[i](0 ≤ I ≤ 3) head node points to the first node of the single linked list with column number I, so that the number of head nodes is MAX{3,4}=4.

1. Then connect all the head nodes h[i](0 ≤ I ≤ 3) to form a circular single linked list of the leading nodes. In this way, it is necessary to add a total head node hm, which stores the number of rows and columns of the sparse matrix.

Cross linked list of sparse matrix B:

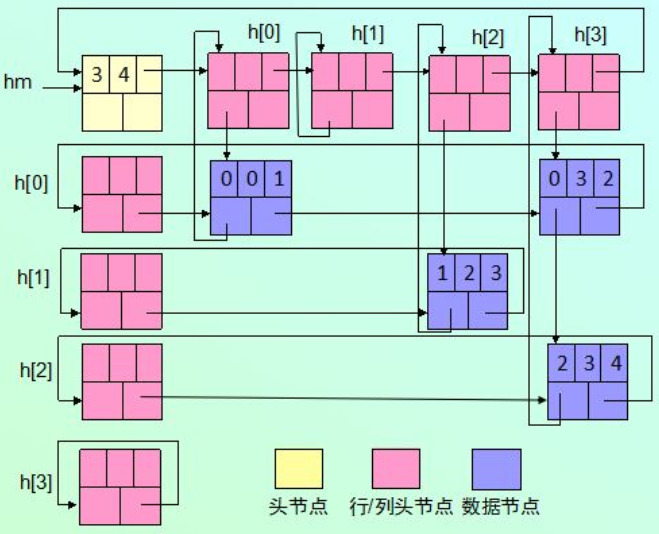
• Each non-zero element is like at an intersection, which is called cross linked list.
• The cross linked list of sparse matrix contains two types of nodes, one is the data node storing non-zero elements, and the other is the head node.
  
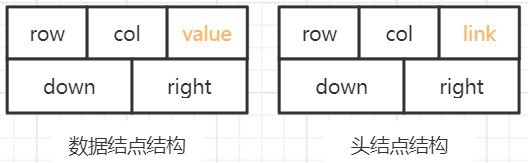
• In order to facilitate the algorithm design, the two types of nodes are unified, and the node type MaxNode of the cross linked list of sparse matrix is designed as follows:

#include<stdio.h>
#Define m < sparse matrix rows >
#Define n < sparse matrix columns >
#Define max (M > n? M: n) / / ternary operator, whichever is greater in the matrix row and column
typedef int ElemType;
typedef struct MatNode
{
	int row; //Line number or number of lines
	int col; //Column number or number
	struct MatNode* right, * down; //Row and column pointers
	union //Common body
	{
		ElemType value; //Non zero element value
		struct MatNode* link; //Point to the next header node
	}tag;
};

• It can be seen that in the cross linked list, the row and column head nodes are shared, and the head node number group is used for storage. Through the h[i] - > right pointer of the head node h[i], all non-zero elements with row subscript i can be searched row by row, and the h[i] - > down pointer can search all non-zero elements with column subscript i column by column. Each non-zero element is contained in two linked lists at the same time, which is convenient for the search of row direction and column direction in the algorithm, so the time complexity of the algorithm is greatly reduced.
• • For an M × N, the total number of head nodes is MAX{m,n}+1.