Stack vs. queue

1. Stack

What is a stack? When we played with toy guns as children, we knew that the stack was like a gun's magazine. Every time a bullet was loaded, the bullet would go down to the bottom of the magazine. But when you hit the bullet, you found that it was from the last bullet you put into the magazine that you started shooting in turn. There are also web page back, word, ps "undo" operations are implemented using the stack.

• Definition of stack

• features

2. Queue

What is a queue? In life, it's similar to a station queuing for ticket checking. After checking the tickets, they leave, and others line up in turn. Another example is input of letters or numbers by keyboard and output in notepad of display.

• Characteristics of the queue

3. Stack and queue

• Similarities

• difference

Storage structure of stack and queue

Storage structure of stack

1. Sequential storage structure of stack

The sequential storage structure of stack is realized by array, where top points to the next storage location of the element storage location at the top of stack.

• Empty operation

	public boolean isElempty() {
		return top == 0;		
		//top can be defined in two ways:
		//1, Set the next storage location that points to the storage location of the top element of the stack. That is to say, when top points to array position 0, there is no data element. When data element is inserted, top will point to the next storage position of the stack top element, and the stack is not empty at this time.
		//2. It can also be defined that the stack is empty when top == -1
	}

• Return to top of stack element operation
  Note: top points to the next position of the top stack element, so the position when returning the top stack element is: top-1 position.

	//Return to the top element of the stack: first, judge whether the stack is empty
	public Object peek() {
		if(!isElempty()) {
			return stackElem[top-1];
		}else {
			return null;
		}
		
	}

• Push operation
  Stack operation: the stack is operated at the top end of the stack. The stack enters one data element at a time, top+1.
  For example: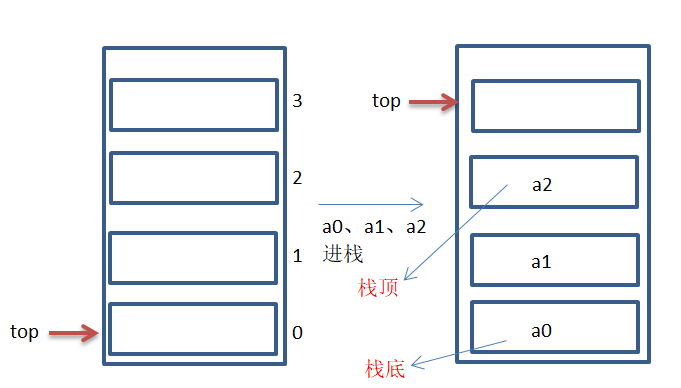
  
  Code implementation:

	public void push(Object x) throws Exception {
		if(top == stackElem.length) {		//stackElem.length Define the length of the storage stack for
			throw new Exception("Stack full");
		}else {
			stackElem[top++] = x;	//x stack top plus 1
			
			//Equivalent to stackElem[top] = x; top = top+1;
		}
	}

• Stack out operation
  Stack out operation: stack out is also operated at one end of the stack top element. Whenever a stack top element is out of the stack, top will first - 1.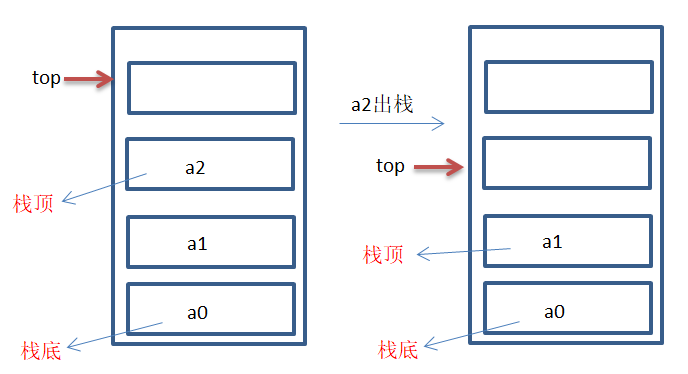
  
  Code implementation:

	//Output stack top element
	public Object pop() {
		if(isElempty()) {
			return null;
		}else {
			return stackElem[--top];	//Top points to the next position of the stack top element, so - 1 is required for top, and only the stack top element is returned
		}
	}

2. Chain storage structure of stack

The top of the stack is placed at the head of the single chain table. You do not need to define the head node like a single chain table. The top of the stack pointer is the head pointer.

Note: Top refers to the top node of the stack. Insertion and deletion are carried out in the header (top of the stack).

• Define a Node node class first

package stack;
/**
 * Create description of node class
 * @author Lazy little black
 *
 */
public class Node {
	//Define data, next node reference (pointer)
	public Object date;
	public Node next;
	
	//Define construction methods with and without parameters
	public Node() {
		 this.date = null;
		 this.next = null;
	}
	public Node(Object date) {
		this.date = date;
		this.next = null;
	}
	public Node(Object date,Node next) {
		this.date = date;
		this.next = next;
	}
	
}

• Judge stack empty and empty operations

public class LinkStack implements IStack{
	public Node top;
	
	public void clear() {
		top = null;
	}
	public boolean isElempty() {
		return top == null;		//Equivalent to: return top==null?true:false;
	}

• Return stack length operation
  Just like single chain table, each node can be traversed.

	//length
	public int length() {
		Node p = top;
		int length = 0; 
		while(p!=null) {
			p = p.next;		//Pointer backward
			++length;		//Length + 1
		}
		return length;
	}

• Top of stack element

	//Top of stack element
	public Object peek() {
		if(isElempty()) {
			return null;
		}else {
			return top.date;
		}
	}

• Push operation
  

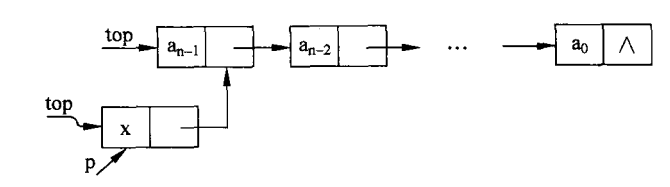
  Note: define the new node P, assign the top of stack pointer (top) to the direct successor (p.next) of the new node, and then assign the new node p to the top of stack pointer.

  Code implementation:

	//Stack pressing
	public void push(Object x) {
		Node p = new Node(x);
		p.next = top;
		top = p;
		
	}

• Stack out operation
  
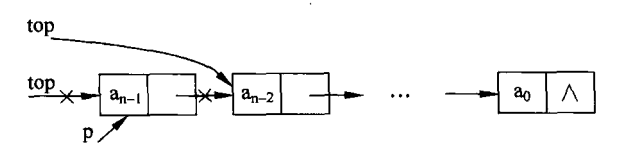
  Note: a p node is used to store the stack node, and then the top pointer of the stack points to the next node.

Code implementation:

	//Out of the stack
	public Object pop() {
		if(isElempty()) {
			return null;
		}else {
			Node p = top;		//Node p stores the nodes out of the stack
			top = top.next;		//Pointer backward
			return p.date;
		}
		
	}

Note:
The time complexity of sequence stack and chain stack is O (1).

Storage structure of queue

1. Sequential storage structure of queues

The sequential storage structure of queues is the same as that of linear tables. However, in the linear table sequential storage structure, if you want to delete the elements (that is, queue out), then the elements behind the queue will move forward, and the time complexity is O (n), which limits the condition that the queue must be stored in the first n cells of the array. Without this restriction, will the performance be greatly improved? So queues are stored in this way.

• Sequential storage of queues

Two pointers are referenced. The front pointer points to the team head element and the rear pointer points to the next position of the team tail element.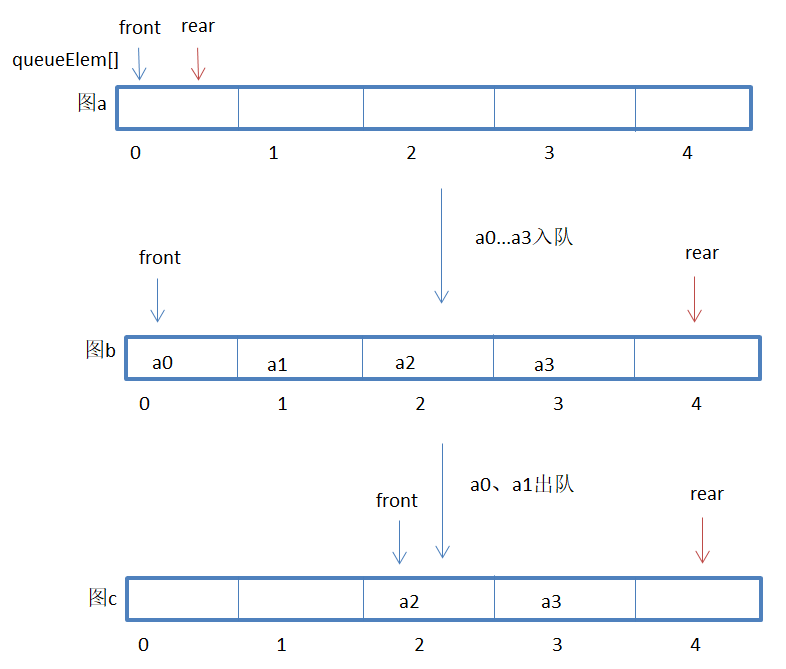

• "False overflow" problem

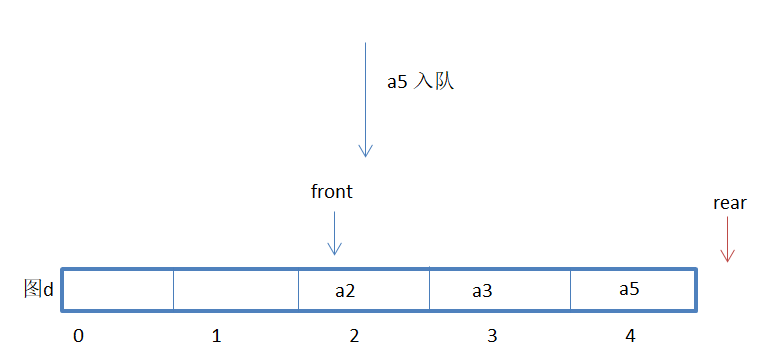
  As assumed above, the total number of this queue is no more than 5. However, in Figure d, if the queue is entered next, the end of the array element queue has been a5 In fact, we find that the subscripts 0 and 1 in the queue are still idle, but they cannot be queued. We call this overflow phenomenon "false overflow".

  If in a bus, you find that the seats in the back are full, and there are seats in the front, would you choose not to go and get off to wait for the next bus? It's not just a waste. I want to hammer you with a hammer! Therefore, in order to solve the problem of "false overflow", the best way is to regard the storage space used by the sequential queue as a logically end-to-end circular queue.

2. Loop queue

• Judgment of team full and team empty

So the real at this time should point to array 0.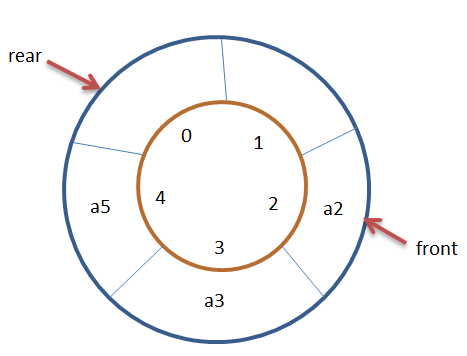

At this time, a6 and a7 are joining the team: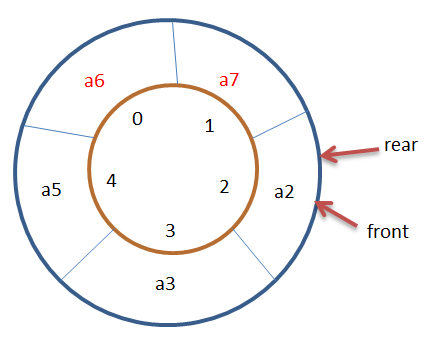

It is found that:
When the queue is empty,

front == rear；

When the team is full

front == rear；

How to judge?
There are many ways to solve this problem:
Method 1:

Method 2:

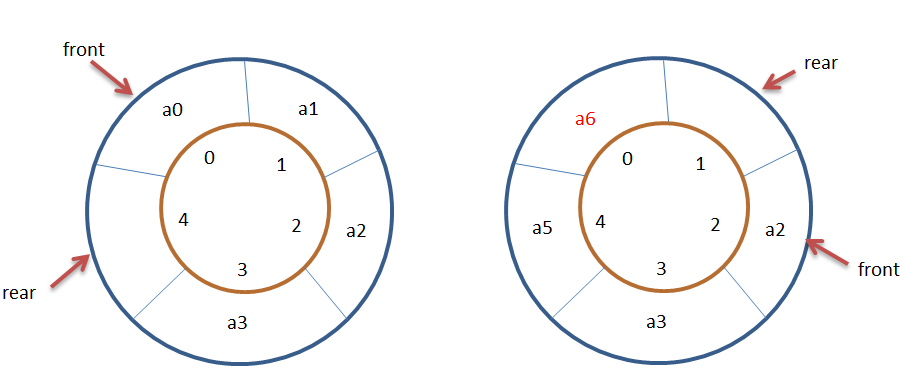
• queue length

  The general formula for calculating queue length is:
  (rear - front + QueueSize)% QueueSize

  We can list all four kinds of situations when front > rear and front < rear (respectively, queue full and queue not full). Then we can analyze the queue length when front > rear and queue length when front < rear respectively, and get the queue length formula.

• Read team head element operation

	//Read team leader element
	public Object peek() {
		if(front == rear) {				//Queue is empty
			return null;
		}else {
			return queueElem[front];
		}
	}

• Entry operation

  Note: the rear always points to the next storage location for the tail element.

	public void offer(Object x) throws Exception {
		if((rear + 1)%queueElem.length == front	) {			//Team full
			throw new Exception("The team is full");
		}else {
			queueElem[rear] = x;							//Join the team
			rear = (rear +1)%queueElem.length;				//Modify end of queue pointer
		}
	}

• Out of line operation

  Note: first take out the value of the team head element, and then cycle the front + 1.

	//Out of the team
	public Object poll() {
		if(front == rear) {									//Team space
			return null;
		}else {
			Object t = queueElem[front];
			front = (front + 1)%queueElem.length;			//front value cycle plus 1
			return t;
		}
	}

Time complexity analysis:
The algorithm time complexity of both entry and exit operations is O (1).

3. Chain storage of queues

The chained storage structure of queues is implemented by a single chained table without leading nodes.

• Node class
  Same as above, but here I encapsulate the properties and add get and set methods for later use.!

• Empty judgment and empty operation

public class LinkQueue implements IQueue {
	private Node front;
	private Node rear;
	
	public LinkQueue() {
		front = rear = null;
	}
	public void clear() {
		front = rear = null;
	}
	public boolean isEmpty() {
		return front == null;
	}

• Calculation length operation

  By traversing each node.

	public int length() {
		Node p = front;
		int length = 0;
		while(p != null) {
			p = p.getNext();	//Pointer down
			++length;
		}
		return length;
	}

• Team leader element

	//Team leader element
	public Object peek() {
		if(front!=null) {
			return front.getDate();
		}else {
			return null;
		}
	}

• Entry operation
  The basic idea is similar to the single chain table without leading nodes, except that the chain queue restricts the insertion at the end of the table.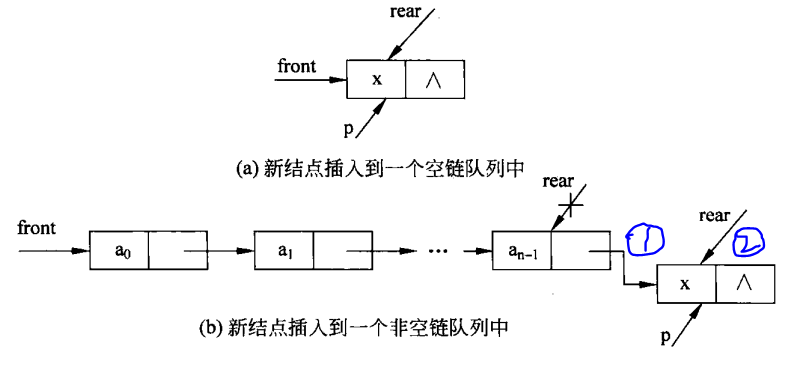
  
  Code implementation:

	//Join the team
	public void offer(Object x) {
		Node p = new Node(x);			//Initialize new node
		if(front != null) {				//Queue is not empty
			rear.setNext(p);			//Assign the p node to the next field where the rear points to the node
			rear = p;					//Change the tail position and assign p to rear
		}else {
			front = rear = p;
		}
	}

• Out of line operation

	//Out of the team
	public Object poll() {
		if(front != null) {
			Node p = front;				//p store the first node out of the queue
			front = front.getNext();	//Point the front to the next node
			return p.getDate();			//Return p-node data field
		}else {
			return null;
		}
	}