expression

• Calculation rules
  From left to right, multiply and divide first, then add and subtract. Brackets count first

• Constituent elements
  Add (+), subtract (-), multiply (*), divide (/), parentheses (()), or spaces ()

• Calculation process
  First convert infix expression into suffix expression, and then evaluate the suffix expression.
  In the specific code implementation, the two steps are mixed together
  Two stacks are needed to realize the calculation. An operand stack for storing operands in expressions; The other is the operator stack, which is used to store the operators in the expression

  Common expressions are infix expressions, such as 9 + (3-1) * 3 + 10 / 2
  Suffix expressions do not contain parentheses, such as 9 3 1 - 3 * + 10 2 /+

• Priority Setting
  Priority for the operators in the expression, there are two types: in stack priority and out of stack priority.

  Whether inside or outside the stack, the priority of multiplication and division is always higher than that of addition and subtraction. The priority of multiplication and division is the same, and the priority of addition and subtraction is the same
  For the same operator, the priority inside the stack is higher than that outside the stack
  Out of the stack, '(') takes precedence over all operators; in the stack, it takes precedence over all operators
  (in case of specific code, '(' is directly put into the stack)
  Out of the stack, ')' takes precedence over all operators; in the stack, it takes precedence over all operators.
  (in case of specific code, ')' will not be put on the stack)
  

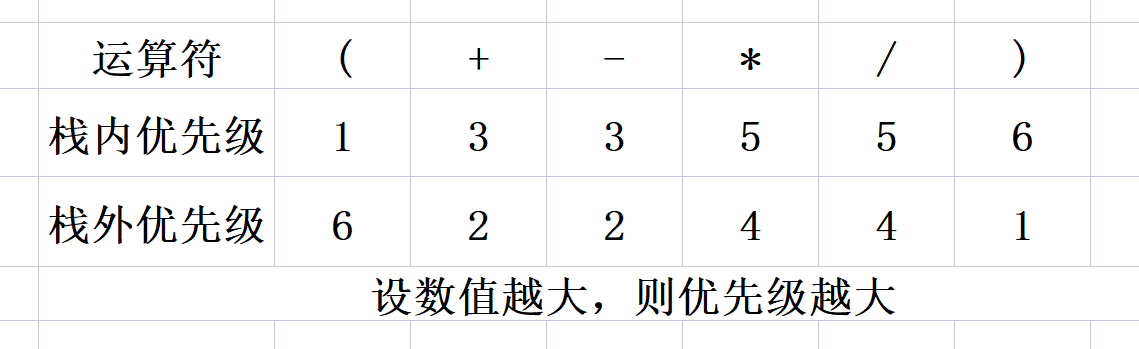
  I personally think that the reason why the priority is divided into in stack and out of stack is due to the "left to right" provision in the calculation rules.
  Assume that there are only two operators with the same priority in the expression, such as 1 + 2 - 3.
  Set the + operator on the left as rope and the - Operator on the right as rope. According to the calculation rules from left to right, rope should participate in the operation before rope.
  In the specific code implementation, you need to scan each character in the expression from left to right, and lope is put on the stack first. When the rope is scanned (at this time, the rope has not been put on the stack, but the rope has been put on the stack), in order to meet the calculation rules from left to right (that is, to realize the purpose of calculating the rope first), it is necessary to give the rope (on the stack) higher operation priority than the rope (off the stack).
  In short, the addition, subtraction, multiplication and division operators have higher priority when they are stacked

#include <iostream>
#include <string>
#include <stack>
using namespace std;

bool isOpe(char ch) // Judge whether it is an addition, subtraction, multiplication and division operator 
{
    switch (ch)
    {
    case '+':
    case '-':
    case '*':
    case '/':
        return true;
    default:
        return false;
    }
}
bool isNum(char ch)
{
    if ((ch - '0') >= 0 && (ch - '0') <= 9)
        return true;
    return false;
}
int cmp(char inStack, char outOfStack)
{
    /* 
		On stack operator inStack off stack operator outOfStack
		The former has high priority and returns a positive number of 1
		The latter has higher priority and returns a negative number - 1
		Elements in the operator stack can only be # + - * /( 
	*/ 
    switch (inStack)
    {
    case '+':
        if (outOfStack == '*' || outOfStack == '/')
        {
            return -1;
        }
        else
        {
            return 1;
        }
    case '-':
        if (outOfStack == '*' || outOfStack == '/')
        {
            return -1;
        }
        else
        {
            return 1;
        }
    case '*':
        return 1;
    case '/':
        return 1;
    case '(':
        if (outOfStack == '+' || outOfStack == '-' || outOfStack == '*' || outOfStack == '/')
        {
            return -1;
        }
    case '#':
        if (outOfStack == '+' || outOfStack == '-' || outOfStack == '*' || outOfStack == '/')
            return -1;
    }
}
double cal(char ch, double num1, double num2)
{
    switch (ch)
    {
    case '+':
        return num1 + num2;
    case '-':
        return num1 - num2;
    case '*':
        return num1 * num2;
    case '/':
        if (num2 == 0)
        {
            cout << "Divisor is 0" << endl;
            exit(-2);
        }
        else
        {
            return num1 / num2;
        }
    }
}

double fun(string str)
{
    /*
		The operator stack OpeStack is set to char type  
		The operand stack NumStack is set to double type (considering division operation)
		Introduce stack in STL to avoid writing two different stack related codes (the same purpose can be achieved by introducing template)	 
	*/
	stack<char> OpeStack;
    stack<double> NumStack;
    
    /*
	  Initially, OpeStack is empty, and subsequent operator priority comparison operations cannot be performed,
	  Therefore, an additional character '#' is put on the stack first to meet subsequent calculations, and its priority is lower than that of '(' on the stack 
	*/ 
    OpeStack.push('#'); 
    
    /*
		Operands in expressions lie between operators and spaces,
		The operand may be only 1 bit, such as 3, or multiple bits, such as 333 
		The num_flag is introduced to mark the first digit of the operand 
		So as to achieve the purpose of allowing multi bit operands to participate in the operation
	*/ 
    bool num_flag = false;
    
    // Scan each character in the expression from left to right 
    for (int i = 0; i < str.length(); i++)
    {
        if (str[i] == ' ') // If the character is a space, skip 
        {
            continue;
        }
        else if (isNum(str[i])) // If the character is a number, the next step is to analyze whether it is a multi bit operand 
        {
            /*
				Take 12 + as an example
				When scanning to 1, num_flag is false, indicating that it is the first digit of number 12,
				    Directly enter NumStack and modify num_flag to true 
				When scanning to 2, num_flag is true, indicating that 2 is not the first digit of the number 12
				    The number that has been put into the stack before 2 needs to be taken out from NumStack. This is the number 1. 
				    Therefore, 1 at the top of NumStack stack stack is taken out of the stack, and 2 form the number 12
				    Then put the complete multi digit number 12 into NumStack
				When scanning to +, non numeric, num_flag is modified to false,
					It indicates that the number of digits in front of it has been scanned 
			*/ 
			
			if (num_flag) // If it is a multi bit operand, the corresponding character is converted to a number 
            {
               /* 
			     STL-stack In, the return type of pop() is void 
			     In order to use the out of stack element, the top element of the stack is taken first, and then the element is out of the stack 
			   */ 
			    double temp = NumStack.top();
                NumStack.pop();
                temp = temp * 10 + str[i] - '0';
                NumStack.push(temp);
                num_flag = true;
            }
            else   
            {
            	// Mark the first digit of the operand and directly stack it
                NumStack.push(str[i] - '0');
                num_flag = true;     
            }
        }
        else if (isOpe(str[i]))  // If the operator of addition, subtraction, multiplication and division is scanned, the priority is compared with the top element of OpeStack 
        {
            num_flag = false;   // It indicates that the number of digits in front of it has been scanned 
            if (cmp(OpeStack.top(), str[i]) < 0) // If the priority of the out of stack operator is high 
            {
                OpeStack.push(str[i]);
            }
            else
            {
            	/*
					If the priority of the out of stack operator is small
				*/
                while (cmp(OpeStack.top(), str[i]) > 0)
                {
                    double num1 = NumStack.top(); 
                    NumStack.pop();
                    double num2 = NumStack.top();
                    NumStack.pop();
                    char ch = OpeStack.top();
                    OpeStack.pop();
                    
                    /*
					 	The left operand of the expression is put on the stack first. NumStack 
						Actual operation order num2 ch num1 
					*/ 
                    double num3 = cal(ch, num2, num1); 
                    NumStack.push(num3);
                }
                OpeStack.push(str[i]);
            }
        }
        else if (str[i] == '(')   // '(' directly into the stack 
        {
            num_flag = false;
            OpeStack.push(str[i]);
        }
        else if (str[i] == ')')  // When scanning to ')', the OpeStack elements are successively out of the stack to participate in the operation until '(' 
        {
            while (OpeStack.top() != '(')
            {
                double num1 = NumStack.top();
                NumStack.pop();
                double num2 = NumStack.top();
                NumStack.pop();
                char ch = OpeStack.top();
                OpeStack.pop();
                double num3 = cal(ch, num2, num1);
                NumStack.push(num3);   // Operation result stacking 
            }
            OpeStack.pop();
        }
    }
    while (OpeStack.top() != '#'/ / take the remaining operators in OpeStack out of the stack to participate in the operation 
    {
        double num1 = NumStack.top();
        NumStack.pop();
        double num2 = NumStack.top();
        NumStack.pop();
        char ch = OpeStack.top();
        OpeStack.pop();
        double num3 = cal(ch, num2, num1);
        NumStack.push(num3);
    }
    return NumStack.top();
}
int main()
{
    string str;// Use a string to get an expression 
    cout << "Enter an expression" << endl;
    cin >> str;
    cout << "The operation result is" << endl;
    cout << fun(str) << endl;
    return 0;
}