Stack implementation inverse Polish calculator
preface
Part I Bowen The stack implementation infix expression calculator has been introduced in. The infix expression shape such as "1 + ((2 + 3) * 4) - 5" is easy to calculate for people, but it is difficult for computers. On the contrary, the suffix expression "1 23 + 4 * + 5 -" is not very convenient for people, but it is convenient and efficient for computers, Therefore, this blog post will explain how to convert infix expression into suffix expression and realize the calculation of suffix expression.
1. Convert infix expression to suffix expression
1.1 ideas
- Two stacks are initialized: the operator stack s1 and the stack s2 for storing intermediate results
- Scan infix expression from left to right
- When a number is scanned, it is stacked s2
- When an operator is scanned, the operation priority of the operator is compared with the operator at the top of s1 stack
- If s1 is empty or left parenthesis ")", it is directly put on the stack
- Otherwise, if the operation priority of the operator is higher than the top priority of the stack, it is directly put on the stack s1
- Otherwise, if the operation priority of the operator is less than or equal to the stack top priority, first put the stack top operator on stack s2, and then put the operator on stack s1
- If the left bracket "(") is scanned, it will be directly put on the stack
- Scan the right parenthesis ")", then pop up the operators of s1 in turn and merge them into stack s2 until the left parenthesis pops up - > this step can offset the left and right parentheses
- Put the remaining operators in s1 on the stack s2 in turn
- Pop up the elements of s2 and output them in turn. The reverse order of the output result is the suffix expression after infix expression conversion
The following is the flow diagram of converting prefix expression "1 + ((2 + 3) * 4) - 5" into suffix expression "1 2 3 + 4 * + 5 -"
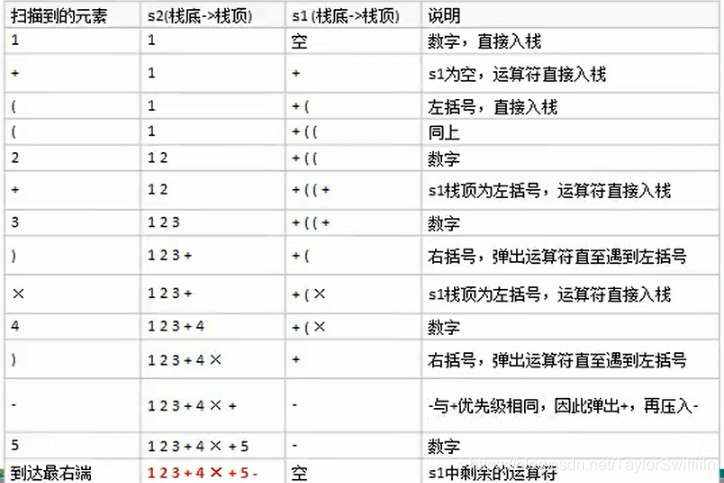
1.2 code implementation
- First convert infix expressions to lists
/**
* Convert infix expression string to list
* @param string
* @return
*/
public static List<String> toInfixExpression(String string)
{
int beginNumberAsciiCode = 48;
int endNumberAsciiCode = 57;
ArrayList<String> list = new ArrayList<>();
//Pointer used to traverse the expression
int i = 0;
//For multi bit splicing
String numBuilder;
//Traverse to a character and put it in c
char c;
do {
//If c is an operator, add it to the list
if ((c = string.charAt(i)) < beginNumberAsciiCode || (c = string.charAt(i))> endNumberAsciiCode)
{
list.add(String.valueOf(c));
//Pointer backward
i++;
}else
{
//Reset
numBuilder = "";
//If it is a number, you need to consider the problem of multiple numbers 0 - > [48] 9 - > [57]
while ((i < string.length() && (c = string.charAt(i)) >= beginNumberAsciiCode && (c = string.charAt(i)) <= endNumberAsciiCode))
{
//Number of spliced multiple bits
numBuilder+=c;
i++;
}
//Add the spliced multi bit number to the list
list.add(numBuilder);
}
}while (i < string.length());
return list;
}
- Convert infix expression list to suffix expression list
/**
* Convert the list of infix expression to the list of suffix expression
* @param list Stores a list of suffix expressions
* @return
*/
public static List<String> parseSuffixExpressionList(List<String> list)
{
Stack<String> operationStack = new Stack<>();
//In fact, the stack should be used, but the stack operation is not required in the whole process, so the list can also be used instead of the stack
List<String> numberStack = new ArrayList<>();
for (String item : list) {
//If it is a number, put it directly on the stack
if (item.matches("\\d+"))
{
numberStack.add(item);
}else if (item.equals("("))
{
operationStack.add(item);
}else if (item.equals(")"))
{
//If it is a right parenthesis, the operators in the symbol stack will pop up in turn. You know that the left parenthesis -- the left and right parentheses are offset
if (!operationStack.peek().equals("("))
{
numberStack.add(operationStack.pop());
}
//Remove the left parenthesis
operationStack.pop();
}else
{
//item is an operator
//When the priority of item operation is less than or equal to the operator at the top of the symbol stack, pop up the operator at the top of the stack and store it in the number stack, and then repeat the above steps
while (operationStack.size() != 0 && getPriority(item) <= getPriority(operationStack.peek()))
{
numberStack.add(operationStack.pop());
}
//When the item operation priority is greater than the operator priority at the top of the symbol stack
//Stack item
operationStack.push(item);
}
}
while (!operationStack.isEmpty())
{
numberStack.add(operationStack.pop());
}
return numberStack;
}
2. Calculation of suffix expression
2.1 ideas
- First, initialize a stack to store the intermediate number
- Scan suffix expression from left to right
- Scan to digital direct stack
- When the operator is scanned, first pop up two numbers in the number stack for operation, get the operation result, and then put the result on the stack
- Repeat the above steps, and the last number in the number stack is the result
2.2 code implementation
/**
* Complete the calculation of the inverse Polish expression
* 1.Scan from left to right to push the number onto the stack
* 2.When encountering an operator, pop up the two elements of the number stack to calculate the result, and then put the result into the number stack
* 3.Repeat the above steps to get the final result
* @param list
* @return
*/
public static int calculate(List<String> list)
{
Stack<String> stack = new Stack<>();
for (String item : list) {
//Regular expression matches multiple bits
if (item.matches("\\d+"))
{
stack.push(item);
}else
{
//Operator: pop out two numbers from the number stack for operation
int num1 = Integer.parseInt(stack.pop());
int num2 = Integer.parseInt(stack.pop());
int result = calculate(num1, num2, item);
stack.push(String.valueOf(result));
}
}
return Integer.parseInt(stack.pop());
}
/**
* Operate the two numbers that pop up
* @param num1
* @param num2
* @param operation
* @return Return the operation result to the stack
*/
private static int calculate(int num1, int num2, String operation)
{
int result = 0;
switch (operation)
{
case "+":
result = num2 + num1;
break;
case "-":
//Pay attention to the order
result = num2 - num1;
break;
case "*":
result = num2 * num1;
break;
case "/":
//Pay attention to the order
result = num2 / num1;
break;
default:
throw new RuntimeException("Incorrect operator,Please re-enter....");
}
return result;
}
3. Test
public class PolandNotation
{
public static void main(String[] args)
{
String expression = "1+((2+3)*4)-5";
List<String> list = toInfixExpression(expression);
System.out.println(list);
List<String> parseSuffixExpressionList = parseSuffixExpressionList(list);
System.out.println(parseSuffixExpressionList);
int result = calculate(parseSuffixExpressionList);
System.out.println("Result:"+result);
}
}
//---------------------------------------------------Output results------------------------------------------------------
OriginalList ---> [1, +, (, (, 2, +, 3, ), *, 4, ), -, 5]
parseSuffixExpressionList ---> [1, 2, 3, +, 4, *, +, 5, -]
Result:16
above.
If there are deficiencies or errors, please comment and correct.