What is a linear table for?
(sequential list and linked list) linear storage data
Stack concept: implemented with linear table - last in first out - LIFO last in first out
Stack (also known as stack): a container that can store data elements for access and deletion
Single end operation: it is only allowed to add (push) and output (pop) data at one end of the container (TOP of the stack)
There is no location concept and can be accessed at any time
Default access order: last in first out - LIFO*
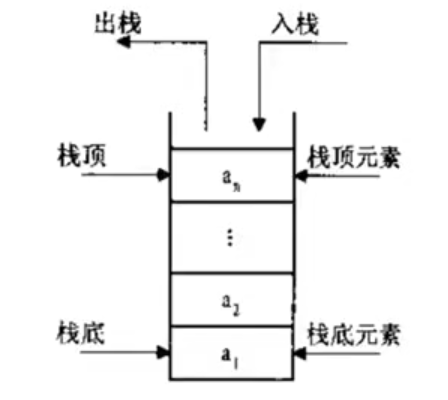
Stack implementation: (you can write a stack with sequential list / linked list)
Actions implemented: – key points
The list tuple adopts the sequential table technology, so there is no need to rewrite the sequential table class. It can directly use the list for auxiliary storage - just meet the characteristics of first in first out stack
Stack() creates a new empty stack
push(item) adds a new element item to the top of the stack
pop() pop up stack top element
peek() returns the stack top element
is_empty() determines whether the stack is empty
size() returns the number of elements in the stack
**Code (implemented with sequence table): * * list tuple adopts sequence table technology, so there is no need to rewrite the sequence table class, and the list can be directly used for auxiliary storage
class Stack(object):
"""Stack"""
def __init__(self):
self.items = []#Define a list to assist storage (sequential table)
def is_empty(self):
"""Judge whether it is empty"""
return self.items == []
def push(self, item):
"""Add element"""
self.items.append(item)#The list can directly call the relevant addition and deletion functions
def pop(self):
"""Pop up element"""
return self.items.pop()
def peek(self):
"""Return stack top element"""
return self.items[len(self.items)-1]
def size(self):
"""Returns the size of the stack"""
return len(self.items)
if __name__ == "__main__":
stack = Stack()
stack.push("hello")#Save string
stack.push("world")
stack.push("itcast")
print stack.size()
print stack.peek()
print stack.pop()
print stack.pop()
print stack.pop()
Queue (first in first out) - FIFO first in first out
It's a linear table
**Operation at both ends: * * it is allowed to insert at one end (the end of the queue) and delete at the other end (the head of the queue)
The middle part cannot be operated
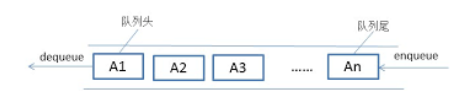
Operation - implemented with sequence table technology
Queue() creates an empty queue
enqueue(item) adds an item element to the queue
dequeue() deletes an element from the queue header
is_empty() determines whether a queue is empty
size() returns the size of the queue
class Queue(object):
"""queue"""
def __init__(self):
self.items = []
def is_empty(self):
return self.items == []
def enqueue(self, item):
"""Enter queue"""
self.items.insert(0,item)
def dequeue(self):
"""Out of queue"""
return self.items.pop()
def size(self):
"""Return size"""
return len(self.items)
if __name__ == "__main__":
q = Queue()
q.enqueue("hello")
q.enqueue("world")
q.enqueue("itcast")
print q.size()
print q.dequeue()
print q.dequeue()
print q.dequeue()
Queue - upgraded - Dual Ended queue
·It has the properties of queue and stack
Elements can pop up from both sides
You can join and leave the team at either end of both sides
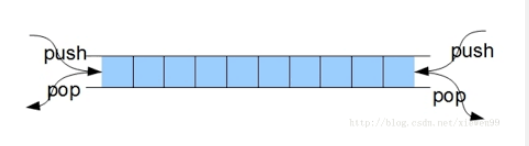
Related operations: – also implemented by sequence table
Deque() creates an empty double ended queue
add_front(item) adds an item element from the team head
add_rear(item) adds an item element from the end of the queue
remove_front() deletes an item element from the queue header
remove_rear() deletes an item element from the end of the queue
is_empty() determines whether the double ended queue is empty
size() returns the size of the queue
class Deque(object):
"""Double ended queue"""
def __init__(self):
self.items = []
def is_empty(self):
"""Determine whether the queue is empty"""
return self.items == []
def add_front(self, item):
"""Add an element to the queue header"""
self.items.insert(0,item)
def add_rear(self, item):
"""Add element at end of queue"""
self.items.append(item)
def remove_front(self):
"""Delete element from queue header"""
return self.items.pop(0)
def remove_rear(self):
"""Delete element from end of queue"""
return self.items.pop()
def size(self):
"""Returns the queue size"""
return len(self.items)
if __name__ == "__main__":
deque = Deque()
deque.add_front(1)
deque.add_front(2)
deque.add_rear(3)
deque.add_rear(4)
print deque.size()
print deque.remove_front()
print deque.remove_front()
print deque.remove_rear()
print deque.remove_rear()
Sorting algorithm - common sorting
1, What is the stability of the algorithm (the less the sorting moves (the less the number of element exchanges), the better the stability)
Stability of the algorithm: it is assumed that there are multiple records with the same keyword in the record sequence to be sorted. If they are sorted, the relative order of these records remains unchanged, that is, in the original sequence, ri=rj, and ri is before rj, while in the sorted sequence, ri is still before rj, then the sorting algorithm is said to be stable; Otherwise, it is called unstable.
For example:
Original sequence:

After sorting: compared with the previous sequence to be sorted, the smaller the change after sorting, the better the stability
2, Importance of algorithm stability
Why is algorithm stability so important?
1) In practical applications, what we exchange is not necessarily an integer, but a large object, and there is a certain overhead in exchanging elements;
2) Referring to cardinality sorting (which will be described later), unstable sorting cannot complete cardinality sorting
Eight sorting methods
1. Bubble Sort - stable
1.1 the operation of bubble sorting algorithm is as follows:
Compare adjacent elements. If the first one is larger than the second (in ascending order), exchange them.
Do the same for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end. After this step, the last element will be the maximum number.
Repeat the above steps for all elements except the last one.
Continue to repeat the above steps for fewer and fewer elements at a time until no pair of numbers need to be compared.
2. Logical analysis

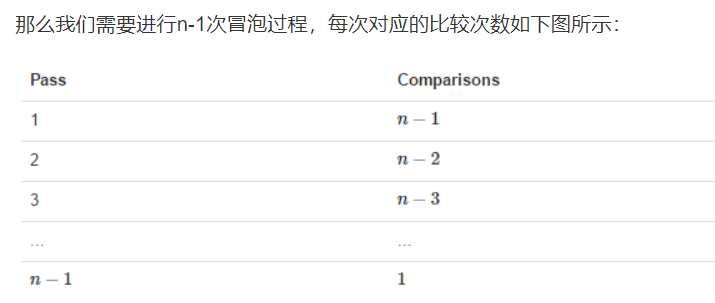
3. Time complexity
Optimal time complexity: O(n) (indicates that no elements can be exchanged after traversing once, and the sorting ends.)
Worst time complexity: O(n2)
Stability: stable
def bubble_sort(alist):
for j in range(len(alist)-1,0,-1):#Range (start point, end point, step size). Here, it means to decrease by one every time, from n-1 to 1. Because the end point of range cannot be obtained, it can be up to 1 here (actually, the end point step size is obtained)
# j represents the number of times to compare each traversal, which decreases gradually
for i in range(j):
if alist[i] > alist[i+1]:
alist[i], alist[i+1] = alist[i+1], alist[i]
li = [54,26,93,17,77,31,44,55,20]
bubble_sort(li)
print(li)
2. Selection sort - unstable
2.1 working principle
·Find the smallest (large) element in the unordered sequence and store it at the beginning of the sorted sequence
·Then continue to find the smallest (large) element from the remaining unordered elements, and then put it at the end of the sorted sequence.
And so on until all elements are sorted
Select sort to exchange a pair of elements each time, and at least one of them will be moved to its final position. Therefore, sort the table of n elements and exchange at most n-1 times in total.
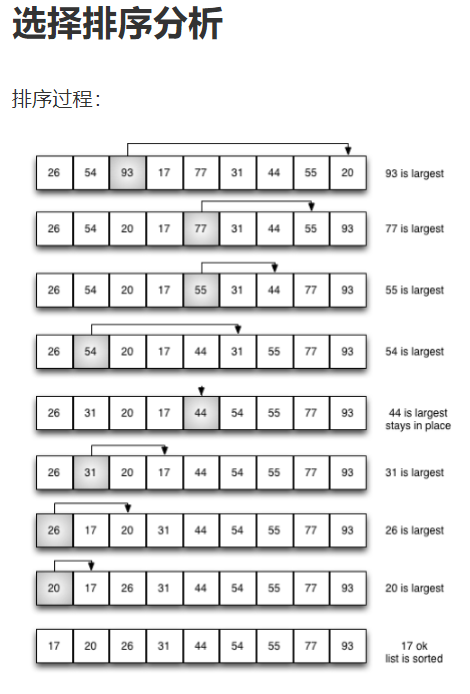
2.2 time complexity
Optimal time complexity: O(n2)
Worst time complexity: O(n2)
Stability: unstable (considering the maximum selection of ascending order each time)
2.3 code
def selection_sort(alist):
n = len(alist)
# n-1 selection operations are required
for i in range(n-1):
# Record minimum position
min_index = i
# Select the minimum data from the i+1 position to the end
for j in range(i+1, n):
if alist[j] < alist[min_index]:#Compare the value of the initial minimum position i position with the minimum value found later between i+1 and n to see who is smaller and assign the smaller position to min_index as the minimum bit
min_index = j
# If the selected data is not in the correct position, that is, the selected number is not the minimum bit set at the beginning, it is exchanged
if min_index != i:
alist[i], alist[min_index] = alist[min_index], alist[i]
alist = [54,226,93,17,77,31,44,55,20]
selection_sort(alist)
print(alist)
3. Insertion Sort * * – stable**
Principle: by constructing an ordered sequence, for unordered data, scan from back to front in the sorted sequence, find the corresponding position and insert it. In the implementation of insertion sorting, in the process of scanning from back to front, it is necessary to repeatedly move the sorted elements back step by step to provide insertion space for the latest elements.
code:
def insert_sort(alist):
# Insert forward from the second position, the element with subscript 1 (the first element is regarded as the initial fixed sequence)
for i in range(1, len(alist)):
# Compare forward from the ith element. If it is less than the previous element, exchange the position
for j in range(i, 0, -1):
if alist[j] < alist[j-1]:
alist[j], alist[j-1] = alist[j-1], alist[j]
alist = [54,26,93,17,77,31,44,55,20]
insert_sort(alist)
print(alist)
Time complexity
Optimal time complexity: O(n) (in ascending order, the sequence is already in ascending order)
Worst time complexity: O(n2)
Stability: stable
4. Quicksort
4.1 principle:
Pick out an element from the sequence, which is called "pivot",
Reorder the sequence. All elements smaller than the benchmark value are placed in front of the benchmark, and all elements larger than the benchmark value are placed behind the benchmark (the same number can be on either side). After the partition is completed, the benchmark is in the middle of the sequence. This is called partition operation.
Recursively sorts subsequences that are smaller than the reference value element and subsequences that are larger than the reference value element.
def quick_sort(alist, start, end):
"""Quick sort"""
# Recursive exit condition
if start >= end:
return
# Set the starting element as the base element to find the position
mid = alist[start]
# low is the cursor moving from left to right on the left of the sequence
low = start
# high is the cursor moving from right to left on the right side of the sequence
high = end
while low < high:
# If low does not coincide with high, and the element pointed by high is not smaller than the reference element, high moves to the left
while low < high and alist[high] >= mid:
high -= 1
# Put the element pointed to by high in the position of low
alist[low] = alist[high]
# If low does not coincide with high, and the element pointed to by low is smaller than the base element, low moves to the right
while low < high and alist[low] < mid:
low += 1
# Put the element pointed to by low in the high position
alist[high] = alist[low]
# After exiting the loop, low coincides with high, and the indicated position is the correct position of the datum element
# Place the base element in this position
alist[low] = mid
# Quick sort the subsequence to the left of the base element
quick_sort(alist, start, low-1)
# Quick sort the subsequence to the right of the base element
quick_sort(alist, low+1, end)
alist = [54,26,93,17,77,31,44,55,20]
quick_sort(alist,0,len(alist)-1)
print(alist)
Time complexity
Optimal time complexity: O(nlogn)
Worst time complexity: O(n2)
Stability: unstable