data structure
C++

strand

Several concepts

  substring and main string: the substring s2 composed of any consecutive characters in the string s1 is called the substring of s1, and s1 is called the main string of s2
  substring position: the position of the first character of the substring in the main string for the first time
  equal: the length of two strings is equal, and the characters in the corresponding position are equal

Sequential string definition

Array form
Character array representation
Defines the maximum length of the string in advance
Take a special character ('\ 0') as the end flag of the string
Method 1

#define MAXNUM / * maximum number of characters allowed for string*/
typedef struct
{
    char c[MAXNUM];
    int n; /* Length of string, n  MAXNUM */
} SeqString;

Method 2

typedef struct
{
    char *str;
    int length;
} STRING;

Chained string definition

typedef struct StrNode
{
    char c;
    struct StrNode *next;
} Lstring, *LinkedString; /* Type of chain */

The main disadvantage of single linked list method is low storage efficiency

Improved method: combine it with the idea of sequential representation, and the nodes of each linked list store multiple characters in sequence.
This not only improves the storage efficiency, but also retains the flexibility of the linked list;
Disadvantages: it adds a little management complexity

Improved definition

#define CHUNKSIZE 80 / / user definable block size
typedef struct StrNode
{
    char c;
    struct StrNode *next;
} Lstring, *LinkedString; /* Type of chain */

typedef struct Chunk
{//Node structure 
	char ch[CHUNKSIZE];
    struct Chunk *next;
} Chunk;

typedef struct   
{//Linked list structure of string
    Chunk *head, *tail;//Pointer to the beginning and end of the string 
    int curlen;//The current length of the string
}LString;

Since the number of characters in the string is not necessarily an integral multiple of the number of characters stored in each node, special characters need to be filled in the empty position of the last node.

The advantage of this storage form is that the storage density is higher than the storage form with node size of 1;
The disadvantage is that the operation of inserting and deleting characters may cause the movement of characters between nodes, and the implementation of the algorithm is complex.

Create empty sequence string

See above for definition

STRING STRINGInit()
{
    STRING *s;
    s->str = new char[1];
    s->str[0] ='\0';
    s->length = 0;
    return s;
}

Sequential string assignment

int StringAssign(STRING *s, *t)
{
    if (s->str) delete (s->str);
    int len = t->length;
    s->length = len;
    if (len == 0)
    {
        s->str = new char[1];
        s->str[0] ='\0';
    }
    else
    {
        s->str = new char[len + 1];
        if (s->str == NULL)
            return ERROR;
        for (int i = 0; i <= len; i++)
            s->str[i] = t->str[i];
    }
    return OK;
}

Sequential string connection

int StringConcat(STRING *s, *t)
{
    STRING temp;
    StringAssign(&temp, s);
    int len = s->length + t->length;
    s->length = len;
    delete (s->str);
    s->str = new char[len + 1];
    if (!s->str) return ERROR;
    else{
        for (int i = 0; i < temp.length; i++)
            s->str[i] = temp.str[i];
        for (int j = 0; j <= t->length; j++, i++)
            s->str[i] = t->str[j];
        free(temp.str);
        return OK;
    }
}

Substring positioning (key)

int Index(STRING *s, *t)
{
    int i, j;
    i = j = 0;
    while (i < s->length && j < t->length)
    {
        if (s->str[i] == t->str[j])
        {
            i++;j++;
        }
        else
        {
            i = i - j + 1;//i move back
            j = 0;//Substring starts from scratch
        }
    }
    if (j == t->length)//Length of coincidence substring
        return i - t->length + 1;
        //Returns the starting position of the substring in the main string
    else
        return 0;
}

Algorithm - pattern matching

Positioning operation of substring in main string
The process of finding substrings exactly the same as pattern p from target s

Common algorithms:
1 simple pattern matching
2 head and tail pattern matching algorithm
3 KMP algorithm (pattern matching without backtracking)

Simple pattern matching

thought

• Compare the characters in p with the characters in s in turn: if s0 = p0, s1 = p1,..., sm-1 = pm-1, the matching is successful, and call the operation of finding substring. subStr(s,1,m) is the substring found.
• Otherwise, there must be some i (0 ≤ i ≤ m-1) so that si ≠ pi. At this time, p can be moved to the right by one character, and the characters in p can be compared with those in s from scratch;
• This is repeated until one of the following two cases:
  1. Matching success: when reaching a certain step, si = p0, si+1 = p1,..., si+m-1 = pm-1, subStr(s,i+1,m) is the found (first) substring with the same pattern p
  2. Matching failure: move p until it cannot be compared with s

Advantages: simple and easy to understand
Disadvantages: low efficiency, afraid of backtracking
Time: O(m*n). In the worst case, each comparison will appear at the end. The maximum comparison is N-M + 1, and the total comparison times are m*(n-m + 1). In general, m ＜＜ n

Head and tail pattern matching

First compare the first character of the mode string, then the last character of the mode string, and finally compare the second to n-1 characters of the mode string

(emphasis) pattern matching without backtracking (KMP algorithm)

It was discovered by D.E.Knuth, J.H.Morris and V.R.Pratt.
KMP algorithm
Time complexity O(n)
Trade space for time
The key point of the algorithm is to find the value of k


The value of K depends only on the substring (k is the subscript)

How to find the K value?
Find substring of matched string
That is, find the largest identical substring of the substring, starting with the subscript 0

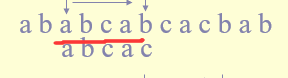
As shown in the figure, abca is a matched substring. Find the same substring from front to back and from back to front, excluding itself
Only a matches here, so k = 1

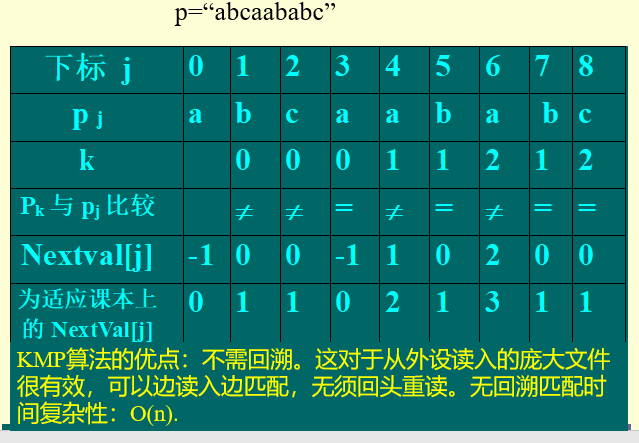
Next array, record K value

When the Next array is known, KMP algorithm can be used quickly

int index(STRING *s, *p, int *next)
{//The Next array is known, that is, the K value is known
    int i, j;
    i = 0;j = 0; /*initialization*/
    while (i < s->length && j < p->length)
    {
        if (j = = -1 || s->str[i] == p->str[j])
        {
            i++;
            j++;
        }
        else
            j = next[j];//And naive pattern matching
            //i does not change, but directly moves the substring
    }
    if (j >= p->length)
        return (i - p->length + 1); /*Match successful*/
    else
        return (0); /*Matching failed*/
}

How to find the Next array is the core of KMP algorithm
In the course of data structure, manual calculation is generally used
Here's how to extend the code
The array of Next is calculated from small to large

void Getnext(int next[],String t)
{//Find the next array, that is, the K value
   int j=0,k=-1;
   next[0]=-1;
   while(j<t.length-1)
   {
      if(k == -1 || t[j] == t[k])
      {
         j++;k++;
         next[j] = k;
      }
      else 
      	k = next[k];//Look forward
   }
}

If Pk and Pj are equal
Further development
Find nextval array
This is the whole, and it solves that Pk and Pj are equal

void Getnext(int next[],String t)
{//Find the next array, that is, the K value
    int j, k;
    k = -1;
    j = 0;
    next[0] = -1;          /* initialization */
    while (j < p.length()) /* Calculate next[j+1] */
    {
        while (k >= 0 && (p[j] != p[k]))
        k = next[k];

        j++;
        k++;
        if (p[j] == p[k])
            next[j] = next[k];
        else
            next[j] = k;
    }
}

Fit diagram understanding