preface

Binary tree is an important part of data structure and belongs to logical structure.
Including: the transformation of tree and binary tree, the transformation of tree into binary tree, and the transformation of forest into tail binary tree.

1, What is a tree?

1. A tree is a finite set of n (n > = 0) nodes. When n=0, it is an empty tree.
2. The tree has only one root node.
3. Except for the root node, each node of the tree can be divided into m (M > 0) disjoint sets, in which each set is a tree.

2, Tree

1. Basic terms of tree

Node: a single cell in a tree

Degree of node: the number of subtrees owned by a node is called the degree of node

Tree degree: the maximum degree of each node in the tree

Leaf: node or terminal node with degree 0

Non terminal node: a node whose degree is not 0

Parents and children: the subtree of a node is called the child of the node. Accordingly, the node is called the child's parents

Brothers: nodes with the same parents are called brothers

Ancestor: from the root node to all nodes on the branch through which the node passes

Descendant: any node in the subtree with a node as the root is called the descendant of the node

Hierarchy: the number of layers of a node is defined from the root. The root is the first layer, and the children of the root are the second layer, and so on.

Cousins: children whose parents are on the same floor are called cousins

Depth of tree: the maximum number of layers in a tree node is called the depth or height of the tree

Ordered tree or unordered tree: each subtree of the node in the tree is ordered from left to right, which is called ordered tree. On the contrary, it is unordered tree.

Forest: a collection of M (M > = 0) trees.

2. Binary tree

1. Binary tree is n(n>=0)A finite set of nodes,n=0 When, it is an empty tree.
2. The degree of each node in the binary tree is not greater than 2
3. The subtree of a binary tree can be divided into left and right
4. There is only one root node

If i If the node is any node of a binary tree, then(2*i)Chu he(2*i+1)They are its left and right children.

Properties of binary tree

Property 1: the second property of binary tree i There are at most 2 on the floor^(i-1)Nodes
 Property 2: depth k There are at most 2 binary trees^k-1 Nodes	
Property 3: for any binary tree, if its terminal node(Leaf node)Tree for N0,The number of nodes with degree 2 is N2，be N0=N2+1

2. Full binary tree (special binary tree)

The number of nodes on each layer is the maximum number of nodes, that is, the number of nodes I of each layer is 2^(i-1)
The full binary tree with depth K has 2^(k-1) nodes

3. Complete binary tree (special binary tree)

Depth is k，And there n Nodes if and only if each node is associated with a depth of k Full binary tree from 1-n The numbers of are one-to-one.

On the basis of full binary tree, the nodes of the last layer decrease from right to left
Leaf nodes can only appear at the two largest levels
For any node, if the maximum number of descendant layers under its right branch is A, then the maximum number of descendant layers under its left branch must be A or A+1

4. Storage structure of binary tree

1.Sequential storage structure

#define SIZEMAX 100
typedef TELemType SqBiTree[SiZEMAX];//1 store root node information
SqBiTree S; 

Take full binary tree as an example
Store the root node in S[1], then its left and right children are placed in S[21] and S[21+1] respectively.
If any node is in S[X], its left and right children are placed at S[2X] and S[2X+1] respectively.

2.Linked Storage Structure 

typedef struct Node
{
	ElemType Data;//Data domain
	struct Node *Lchild;//Left pointer (left child)
	struct Node *Rchild;//Right pointer (right child)
}BiTNode,*BiTree;

5. Traversing binary tree

1.Preorder traversal (Root left and right)
2.Medium order traversal(Zuo Genyou)
3.Postorder traversal(Left and right root)

Take preorder traversal as an example (recursion)

void Traverse(BiTree T)
{
	if(T)
	{
		printf(T->Data);//Every time you enter a node, you first output the node content
		Traverse(T->Lchild);
		Traverse(T->Rchild);
	}
}

The essence of recursively traversing a binary tree is the process of repeatedly pressing and bouncing the stack. (take the following binary tree as an example for analysis)
The result of preorder traversal is 1 2 4 3

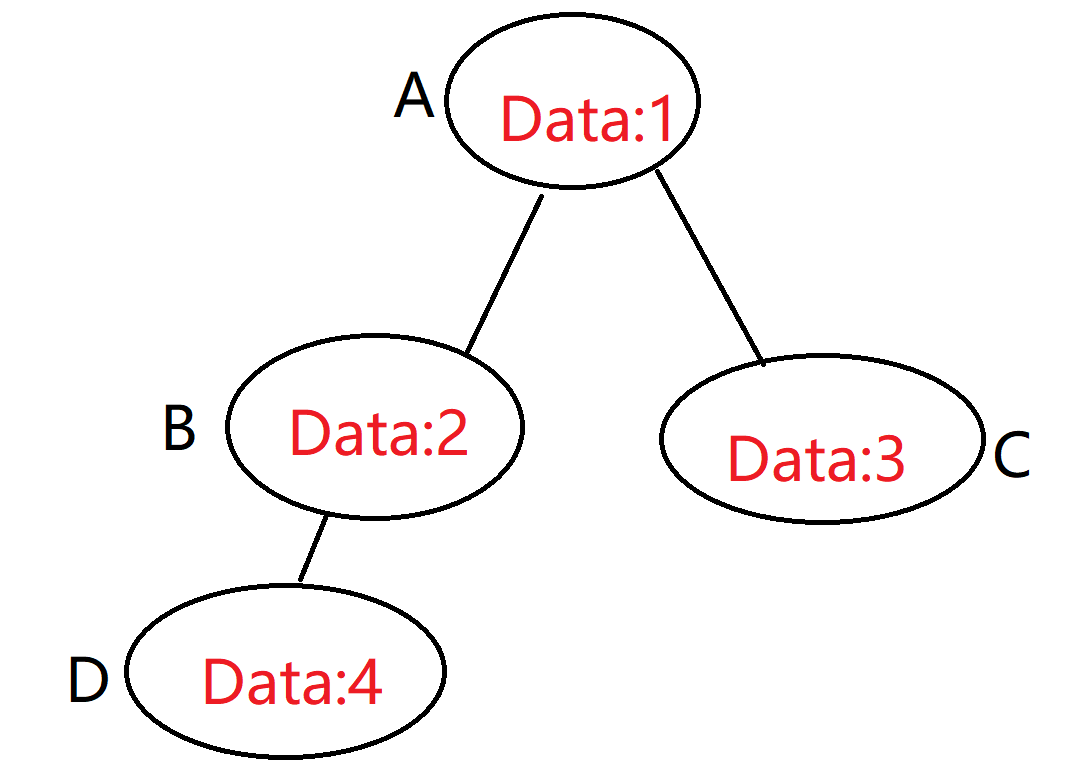
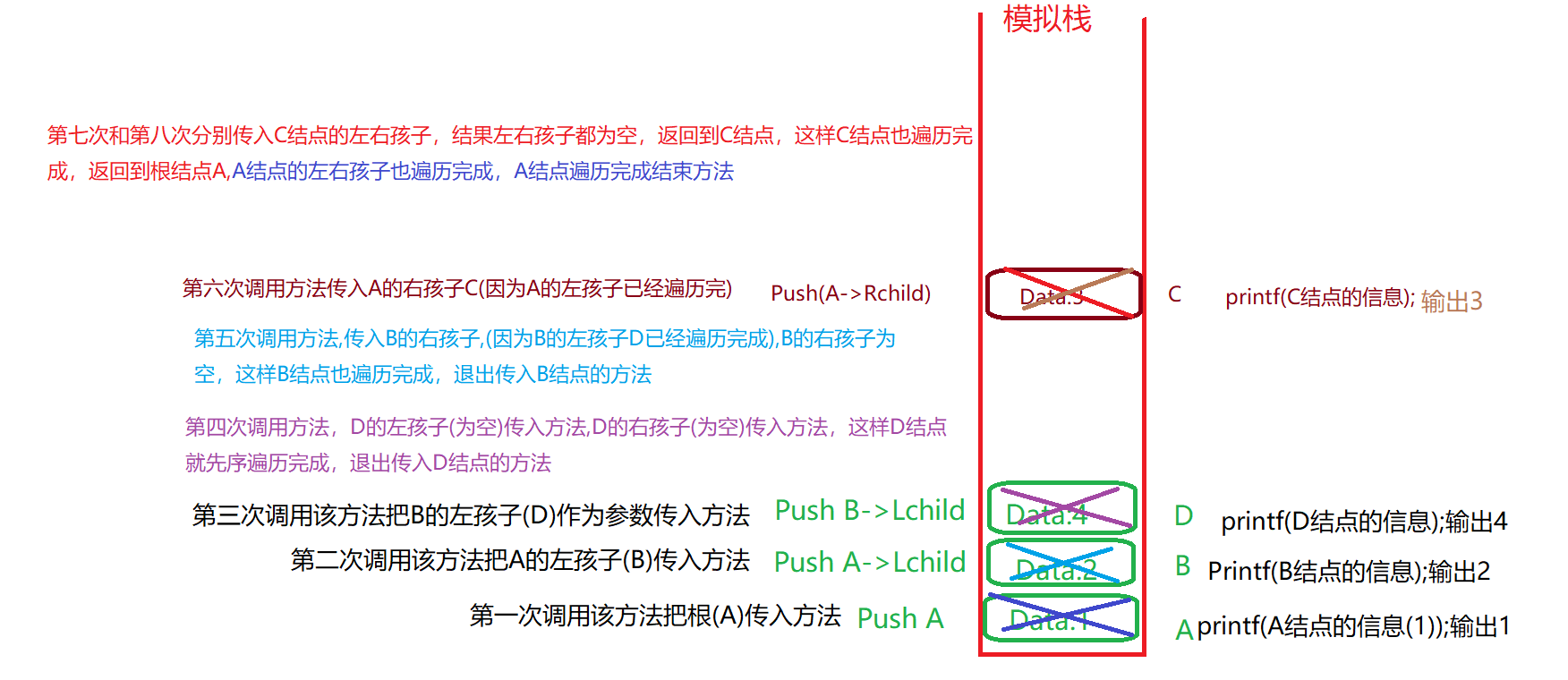
Non recursive traversal of binary tree is to repeatedly press and bounce the stack by using the stack. The first order traversal is similar to the middle order traversal, except that the subsequent traversal is a little different.
Post order traversal should mark each node and record the number of times this node presses the stack.

Let's continue to traverse the binary tree as an example

typedef struct Node
{
	ElemType Data;//Data domain
	struct Node *Lchild;//Left pointer (left child)
	struct Node *Rchild;//Right pointer (right child)
	int flag;//When creating a binary tree, assign the value of flag to 0
}BiTNode,*BiTree;
#define SIZE 10 / / stack length
//Define stack
typedef struct
{
	
	BiTree *arr;//Pointer array (storing data of BiTNode * type, simply storing data of BiTree type)
	//Bitree will point to the address of the BiTNode class node.
	int top;//sign
}Stack;
//Initialization stack
void InitStack(Stack &S)
{
	S.arr=new BiTree[SIZE];
	if(!S.arr)
	{
		printf("Failed to request memory\n");
	}else
	{
		S.top=0;
		printf("Memory request succeeded\n");
	}
	
}
//Stack pressing
void Push(Stack &S,BiTree P)
{
	S.arr[S.top++]=P;
}
//Bomb stack
void Pop(Stack &S,BiTree &P)
{
	P=S.arr[--S.top];
}
//Determine whether the stack is empty
bool AdjustStack(Stack S)
{
	if(S.top)
	{
	return true;
	}else
	{
	return false;
	}
}
//Subsequent traversal of binary tree
void Traverse(BiTree &T)//The reference type is passed in because the flag flag of each node needs to be modified
{
	Stack S;//Define stack
	BiTree Temp;
	InitStack(S);//Initialization stack
	while(T||AdjustStack(S))
	{
		while(T)
		{
			Push(S,T);
			T->flag++;//Mark plus one
			T=T->Lchild;//The pointer moves to the left
		}
		if(AdjustStack(S))
		{
			Pop(S,Temp);
			if(Temp->flag==2)
			{
				printf(Temp->data);//Output the information of this node
			}else
			{
			T=Temp->Rchild;
			Push(S,T);
			T—>flag++;
			}
		}
	}
}

Subsequent recursion only adds one more tag to record the number of times the traversal pointer passes through the node.

6. Clue binary tree

summary

Tip: here is a summary of the article:
For example, the above is what we want to talk about today. This paper only briefly introduces the use of pandas, which provides a large number of functions and methods that enable us to process data quickly and conveniently.