Data Structure - Trees and Binary Trees (Chapter VII). If there are any errors, please correct them.

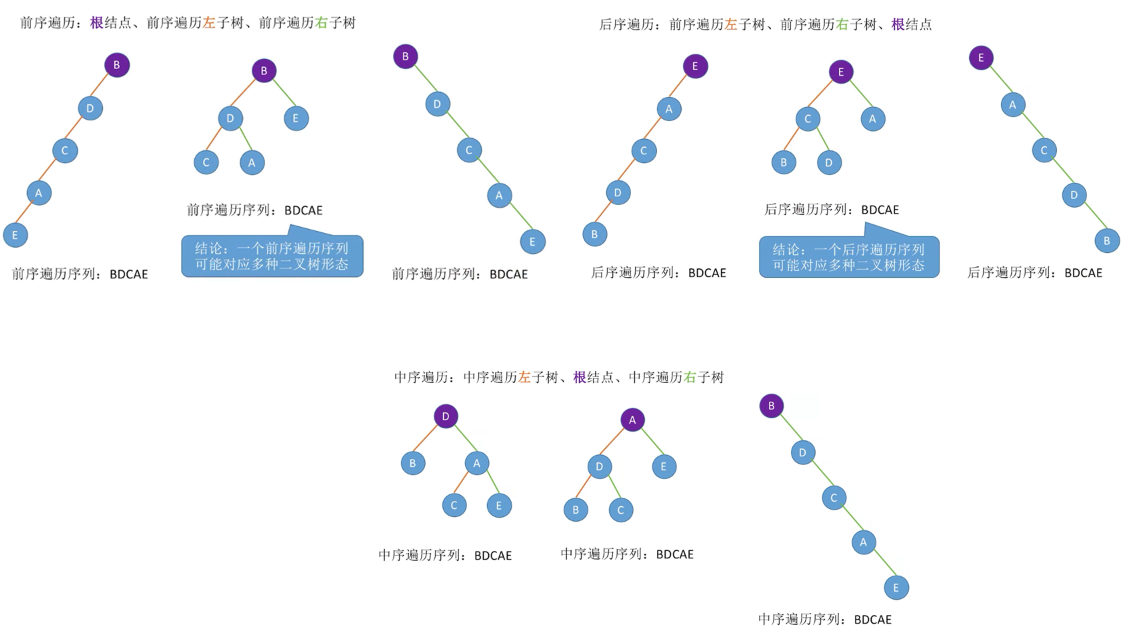
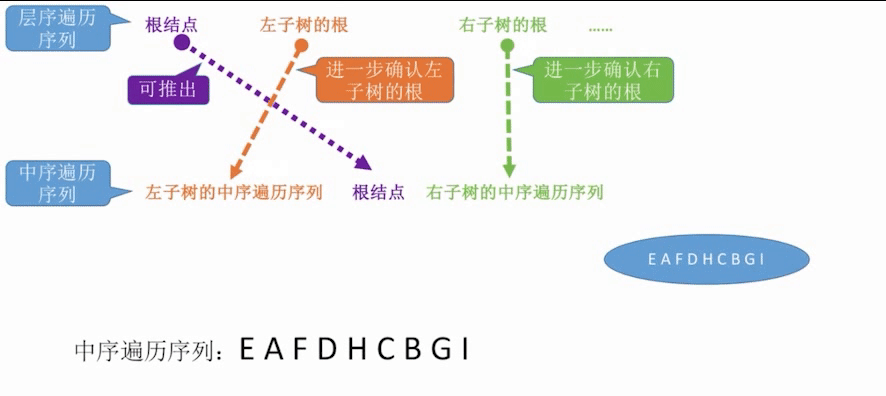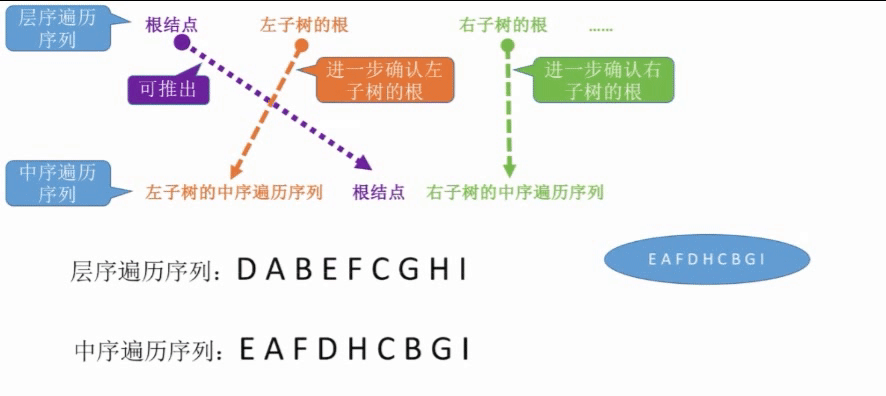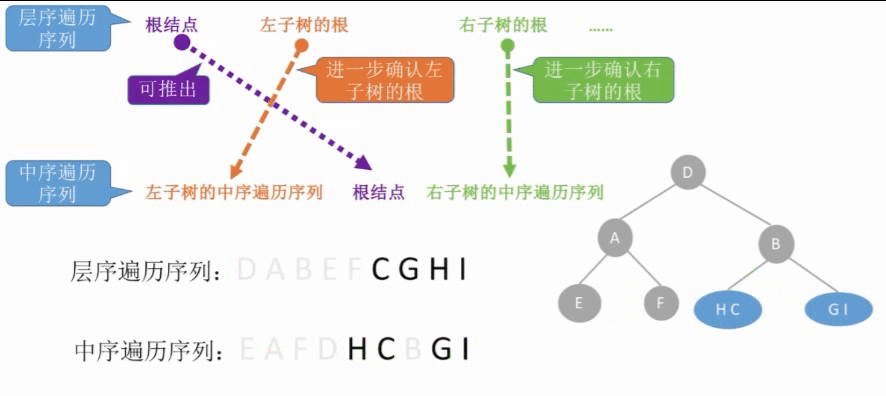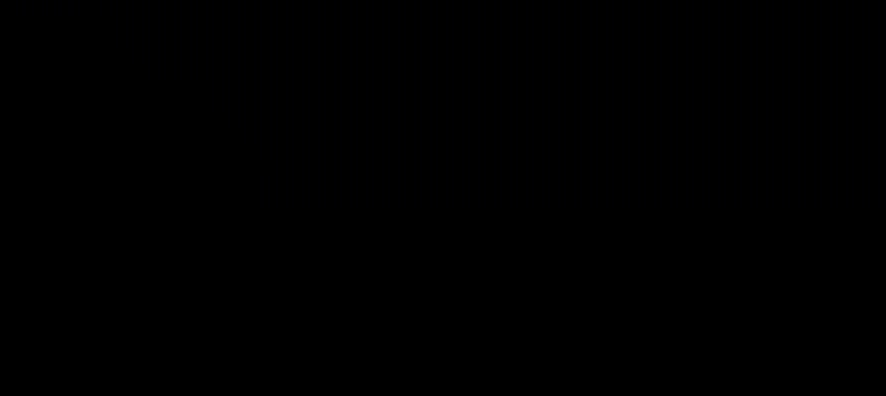
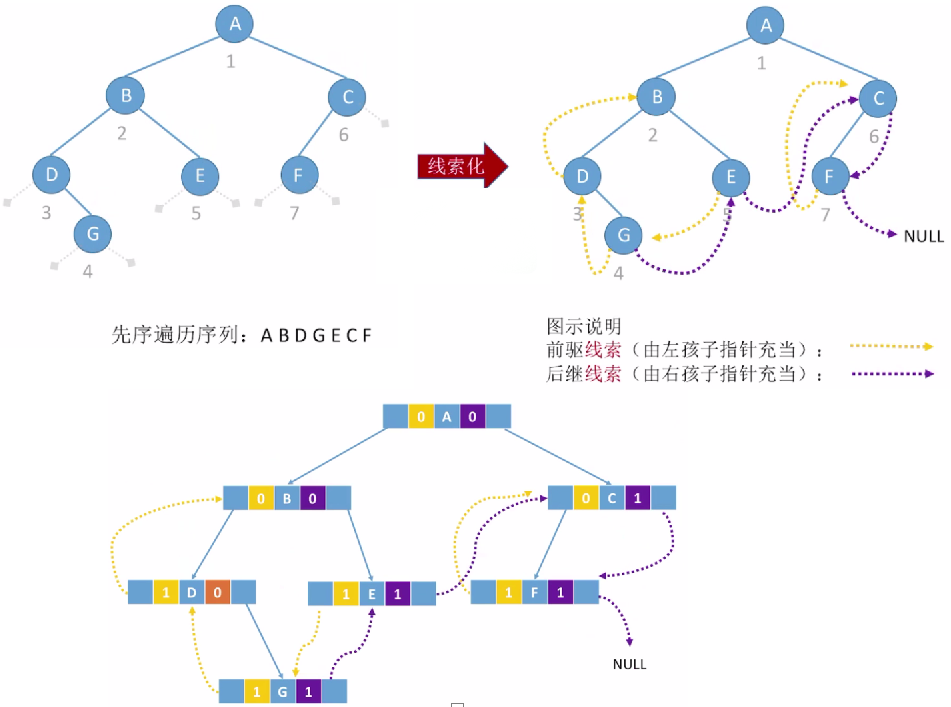
Constructing Binary Trees from Traversal Sequences

Yes can can Of three species feeling condition { Front order + in order Throughout calendar order column after order + in order Throughout calendar order column layer order + in order Throughout calendar order column Three possible scenarios\begin{cases}Pre+Medium Traversal Sequence\Post+Medium Traversal Sequence\Sequence+Medium Traversal Sequence\\end{cases} There are three possible scenarios. Pre-order+Median traversal sequence Post-order+Median traversal sequence sequence sequence+Median traversal sequence sequence

• A binary tree cannot be uniquely identified if only one of the sequence of front/middle/back/sequence traversal of a binary tree is given. In addition, the combination of the precedent, the postorder and the sequence sequence cannot uniquely determine a binary tree.
  

Sequence + Sequence

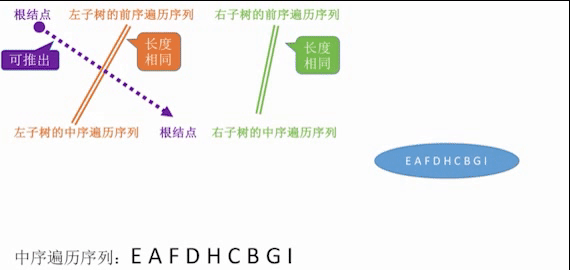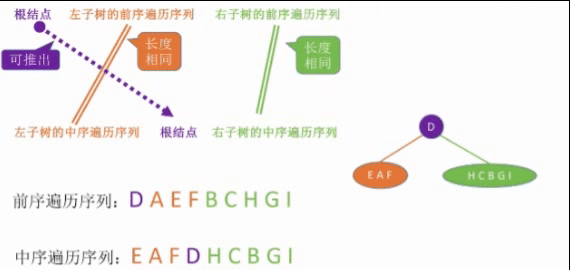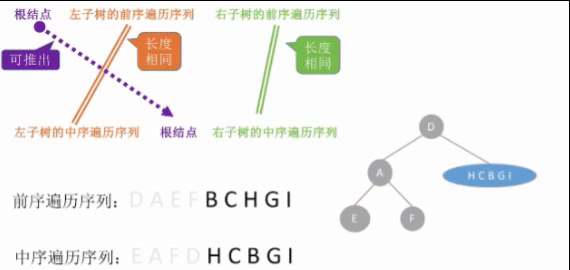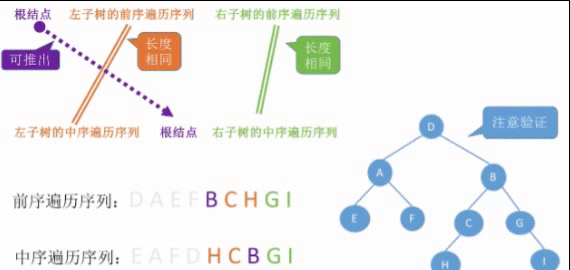
Postordinal + Median Sequences

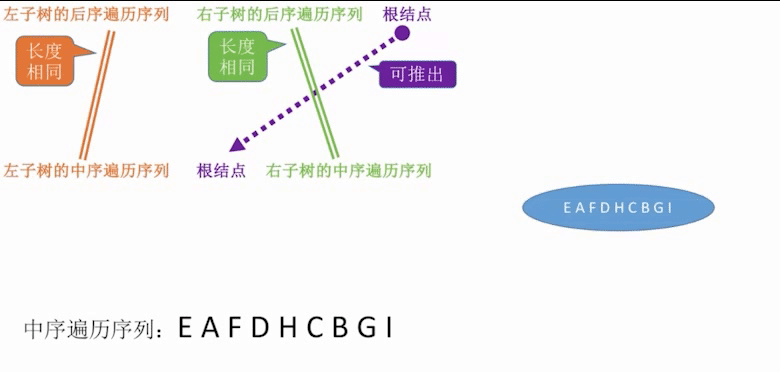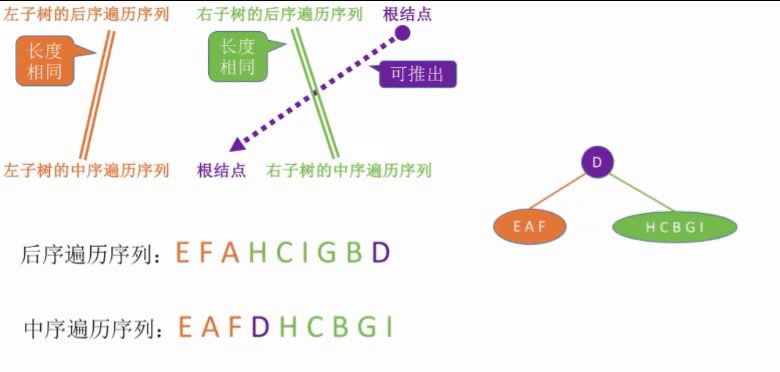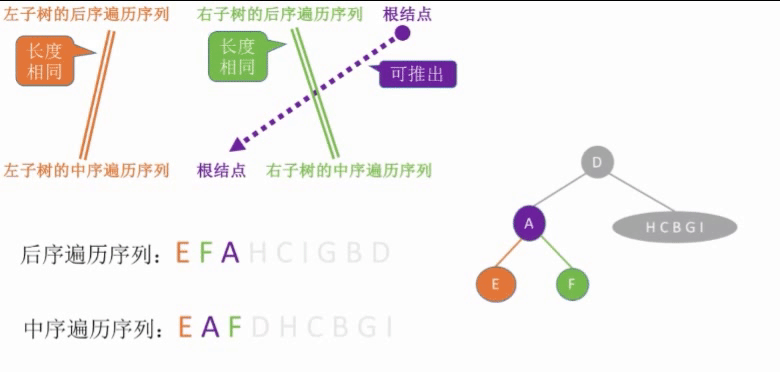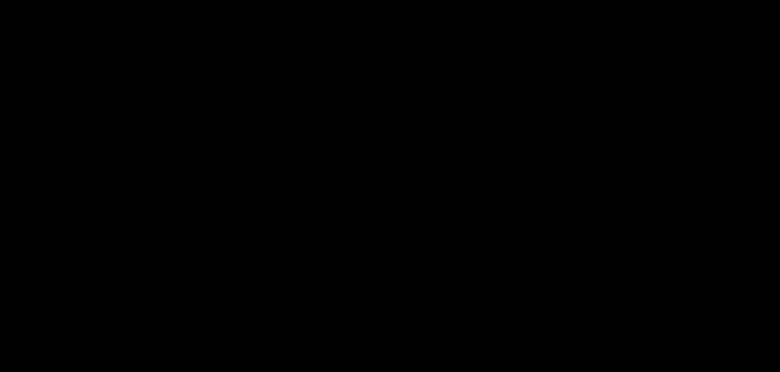
Sequence sequence + Intermediate sequence

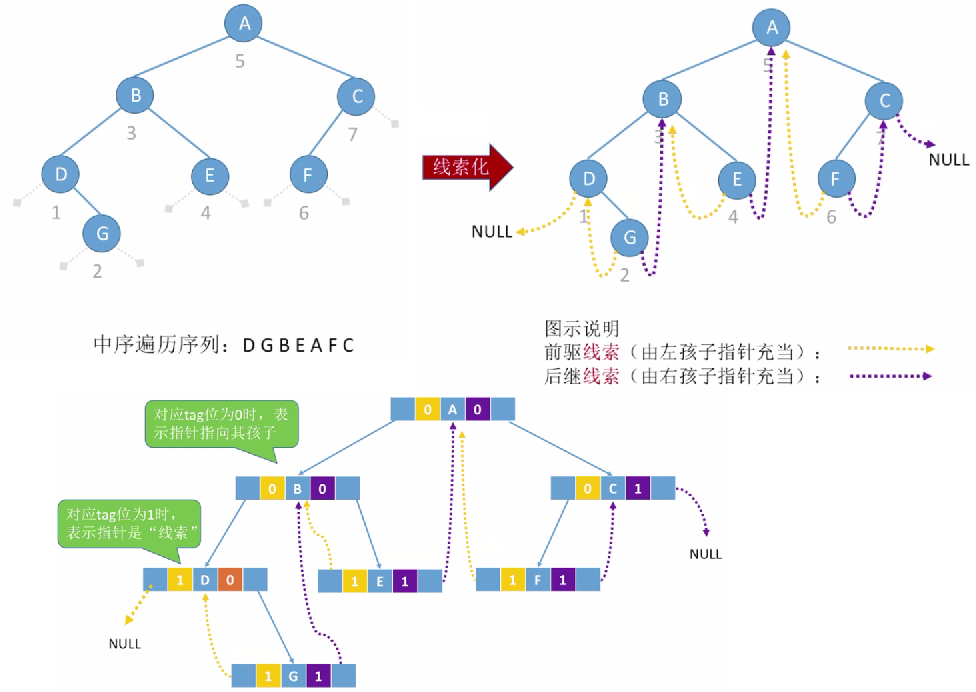
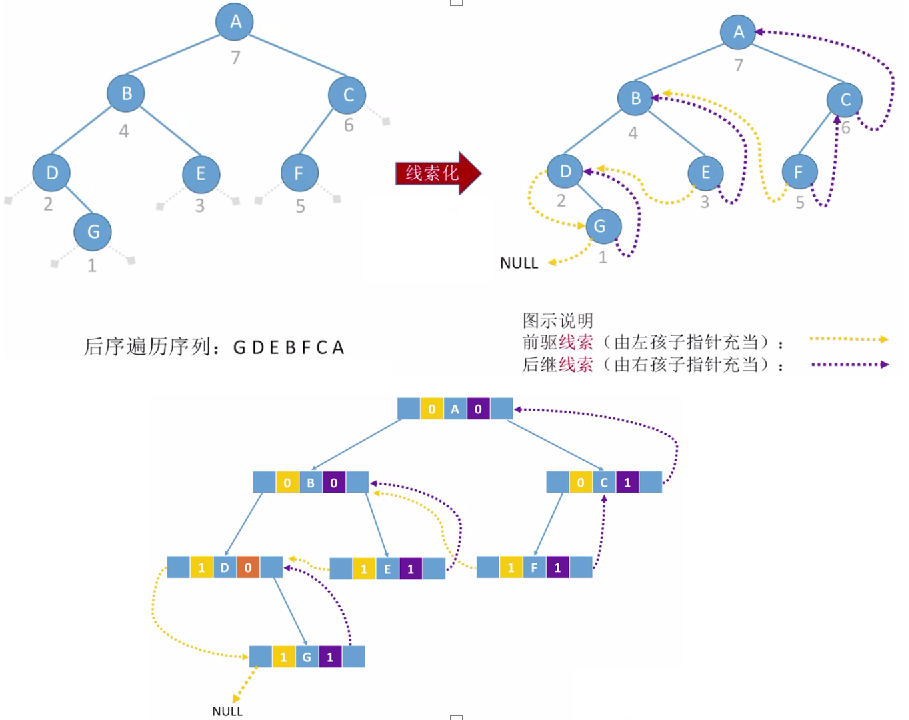
Threaded Binary Tree

• Threaded binary trees are introduced to speed up the search of node precursors and successors, because traditional binary chain lists can only represent a parent-child relationship, and can not directly get the precursors or successors of nodes in traversal.
  Find the intermediate precursor of node p using the original method:

typedef struct BiTNode
{
    ElemType data;
    struct BiTNode* lchild, * rchild;
}BiTNode, * BiTree;

BiTNode* p, * pre = NULL, * final = NULL;

void FindPre(BiTNode *t)
{
    if (t != NULL)
    {
        FindPre(t->lchild); //Recursively traverse left subtree
        visit(t); //Access Root Node
        FindPre(t->rchild); //Recursively traverse right subtree
    }
}

void visit(BiTNode* q)
{
    if (q == p) final = pre; //The current visiting node happens to be node p, finding a precursor to p
    else pre = q; //pre points to the currently accessed node
}

• Provision: If there is no left subtree, make lchild point to its precursor node; If there is no right subtree, make rchild point to its successor nodes. Two additional marker fields are needed to identify whether the pointer field is to the left (right) child or to the front (next).
  
  Among them, the meaning of the flag field is as follows:

l t a g { 0 ，      l c h i l d field finger show junction spot Of Left Child son 1 ，      l c h i l d field finger show junction spot Of Front drive ltag\begin{cases} 0, \;\; The lchild field indicates the left child of the node\1, \;\; The lchild field indicates the precursor\\\end{cases} of the node ltag{0, lchild field indicates left child 1 of the node, lchild field indicates the precursor of the node
r t a g { 0 ，      r c h i l d field finger show junction spot Of right Child son 1 ，      r c h i l d field finger show junction spot Of after Following rtag\begin{cases} 0, \;\; The rchild field indicates the right child of the node\1, \;\; The rchild field indicates the successor\\\end{cases} of the node rtag{0, the rchild field indicates the right child of the node 1, and the rchild field indicates the successor of the node

Description of storage structure of threaded binary tree

typedef struct ThreadNode
{
	ElemType data;
	struct ThreadNode* lchild,*rchild;
	int ltag,rtag;
}ThreadNode,*ThreadTree; 

• The list of binary chains made up of this node structure is called the list of threaded chains as the storage structure of binary trees, and the pointers to the precursors and successors of nodes are called threads. A binary tree with threads is called a threaded binary tree.

Intermediate-order threaded binary tree

Code implementation (headless node)

ThreadNode* pre = NULL;

void CreateInThread(ThreadNode* t)
{
    if(t != NULL) InThread(t); //Non-empty binary trees can be threaded, medium-order threaded binary trees
    if (pre->rchild == NULL) pre->rtag = 1; //Processing the last traversed node
}

void InThread(ThreadNode* t) //Intermediate traversal
{
    if (t != NULL) //Traversing when not an empty tree
    {
        InThread(t->lchild); //Traversing left subtree in middle order
        visit(t); //Access Root Node
        InThread(t->rchild); //Medium-order traversal of right subtree
    }
}

void visit(ThreadNode* q)
{
    if (q->lchild == NULL) //Left subtree is empty, building precursor clues
    {
        q->lchild = pre;
        q->ltag = 1;
    }
    if (pre != NULL && pre->rchild == NULL)
    {
        pre->rchild = q; //Establishing a successor thread for a precursor node
        q->rtag = 1;
    }
    pre = q;
}

Program analysis

Code implementation (with header node)

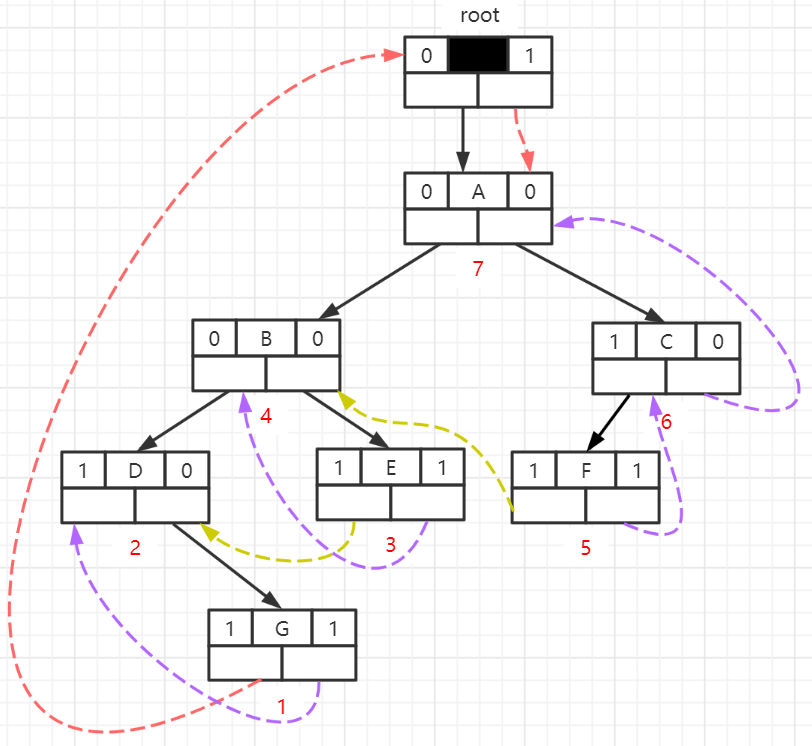
• For convenience, a header node can also be added to the list of binary tree threads, so that the pointer of its lchild field points to the root node of the binary tree, and the pointer of its rchild field points to the last node accessed during the middle traversal. Make the lchild domain pointer of the first node in the sequence of binary trees and the rchild domain pointer of the last node point to the head node. This is like building a two-way threaded list of binary trees to facilitate traversing threaded binary trees from back to front or from back to front.

ThreadNode* pre = NULL; //global variable

void InThread(ThreadNode* &p) //Intermediate threading of binary tree t
{
    if (p != NULL)
    {
        InThread(p->lchild); //Left subtree threading
        if (p->lchild == NULL) //Left child does not exist, threading forward nodes
        {
            p->lchild = pre; //Establishing a precursor node thread for the current node
            p->ltag = 1;
        }
        else p->ltag = 0; //The left subtree of the t-node is threaded
        if (pre->rchild == NULL) //Threading the succeeding nodes of pre p
        {
            pre->rchild = t; //Establishing a successor node thread for a precursor node
            pre->rtag = 1;
        }
        else pre->rtag = 0;
        pre = p;
        InThread(t->rchild); //Right subtree threading
    }
}

ThreadNode* CreatThread(ThreadNode *&t)
{
    ThreadNode* t, * root;
    root = (ThreadNode*)malloc(sizeof(ThreadNode)); //Create Head Node
    root->ltag = 0; //The lchild of the head node points to the left child (that is, to the root node)
    root->rtag = 1; //The rchild of the header node points to the thread (that is, to the last node visited during intermediate traversal)
    root->rchild = t; //The rchild of the first header node points to the root node
    if (t == NULL) root->lchild = pre; //When an empty binary tree is empty, the lchild of the head node points to itself
    else //Binary tree is not empty
    {
        root->lchild = t; //The lchild of the header node points to the root node
        pre = root; //pre is the precursor to node t for threading
        ThreadTree(t); //Intermediate traversal threaded binary tree
        pre->rchild = root; //Finally, add a thread pointing to the head node
        pre->rtag = 1;
        t->rchild = pre; //Head Node Right Threaded
    }
    return root;
}

Program analysis

• The right child pointer of the last node traversed in the middle order must be empty, so instead of determining whether the rchild is NULL, you can directly point the rchild to NULL and make rtag=1.
  

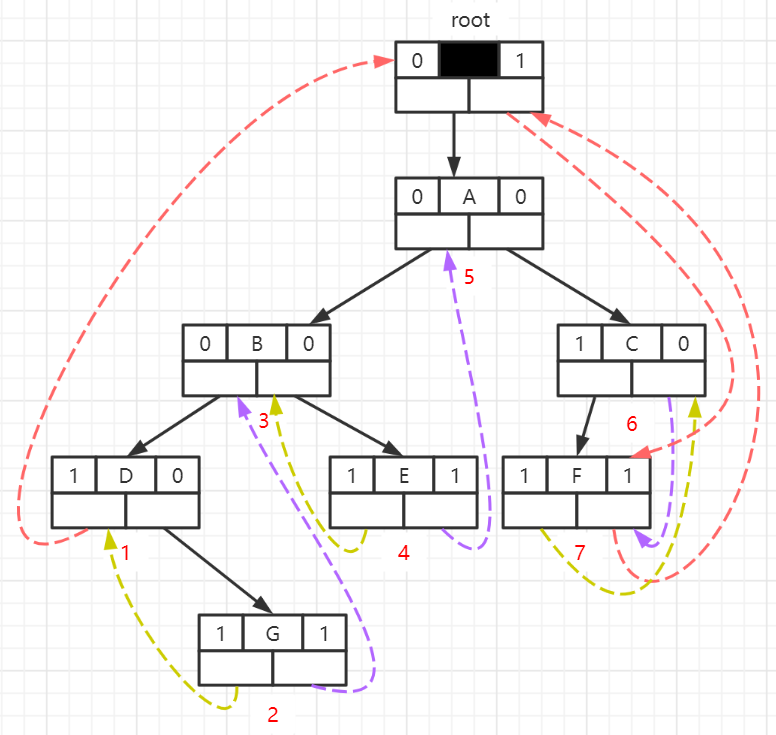
Sequential Threaded Binary Tree

Code implementation (headless node)

ThreadNode* pre = NULL;

void CreatePreThread(ThreadNode* t)
{
    if(t != NULL) PreThread(t); //Non-empty binary trees can be threaded, medium-order threaded binary trees
    pre->rchild == NULL;
    pre->rtag = 1; //Processing the last traversed node
}

void PreThread(ThreadNode* t) //Preorder traversal
{
    if (t != NULL) //Traversing when not an empty tree
    {
        visit(t); //Access Root Node
        if (t->ltag == 0) PreThread(t->lchild); //lchild is not a precursor thread, traversing left subtree in preceding order
        PreThread(t->rchild); //Pre-order traversal of right subtree
    }
}

void visit(ThreadNode* q)
{
    if (q->lchild == NULL) //Left subtree is empty, building precursor clues
    {
        q->lchild = pre;
        q->ltag = 1;
    }
    if (pre != NULL && pre->rchild == NULL)
    {
        pre->rchild = q; //Establishing a successor thread for a precursor node
        q->rtag = 1;
    }
    pre = q;
}

Program analysis

• ! Note: Dead cycle in sequential threading.
  
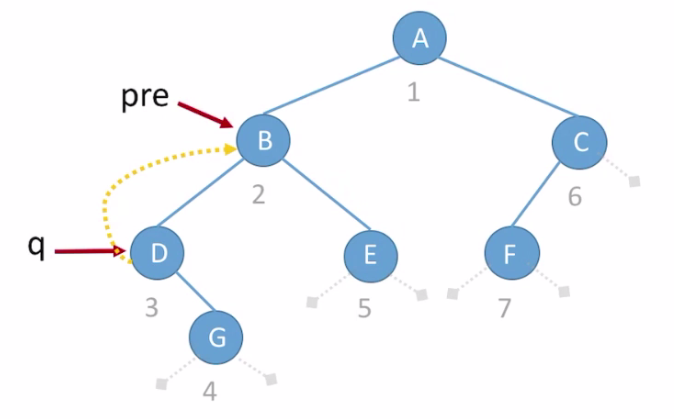
• Assuming that q points to the third node D at this point, the precursor node prep of q should point to the second node B.
• In the order in which the code is executed:

if (q->lchild == NULL) //Left subtree is empty, building precursor clues
    {
        q->lchild = pre;
        q->ltag = 1;
    }

• q.lchild==NULL, let q.lchild point to pre, q.ltag=1.
• The code continues to execute:

if (pre != NULL && pre->rchild == NULL)
    {
        pre->rchild = q; //Establishing a successor thread for a precursor node
        q->rtag = 1;
    }

• At this point although pre!= NULL, but pre. Rchild!= NULL, so skip this part of the code and execute pre = q;.
• Q and prepoint to the third node D at the same time, since the order of sequential access is: around the root. At this point, D is the root node, it should continue to execute the left subtree of D after execution, and D's left child is NULL, which will make q.lchild point to its precursor node, that is, D points back to B again. So the program repeats this over and over again.
• To avoid this endless loop, you can decide if q.lchild is 0 or 1 after the root node is executed, and if it is 1, it represents the left child and threaded, without having to deal with it at this time. Only if q.child is 0, the left child of the root node is not threaded and can proceed.

Code implementation (with header node)

void PreThread(ThreadNode*& p)
{
    if (p != NULL)
    {
        if (p->lchild == NULL)
        {
            p->lchild = pre;
            p->ltag = 1;
        }
        else p->ltag = 0;
        if (pre->rchild == NULL)
        {
            pre->rchild = p;
        }
        if(p->ltag==0) PreThread(p->lchild);
        PreThread(p->rchild);
    }
}

ThreadNode * CreatThread(ThreadNode *&t)
{
    ThreadNode* t, * root;
    root = (ThreadNode*)malloc(sizeof(ThreadNode)); //Create Head Node
    root->ltag = 0; //The lchild of the head node points to the left child (that is, to the root node)
    root->rtag = 1; //The rchild of the header node points to the thread (that is, to the last node visited during the preamble traversal)
    root->rchild = t; //The rchild of the first header node points to the root node
    if (t == NULL) root->lchild = pre; //When an empty binary tree is empty, the lchild of the head node points to itself
    else //Binary tree is not empty
    {
        root->lchild = t; //The lchild of the header node points to the root node
        pre = root; //pre is the precursor to node t for threading
        ThreadTree(t); //Preorder Traversal Threaded Binary Tree
        pre->rchild = root; //Finally, add a thread pointing to the head node
        pre->rtag = 1;
        t->rchild = pre; //Head Node Right Threaded
    }
    return root;
}

Program analysis

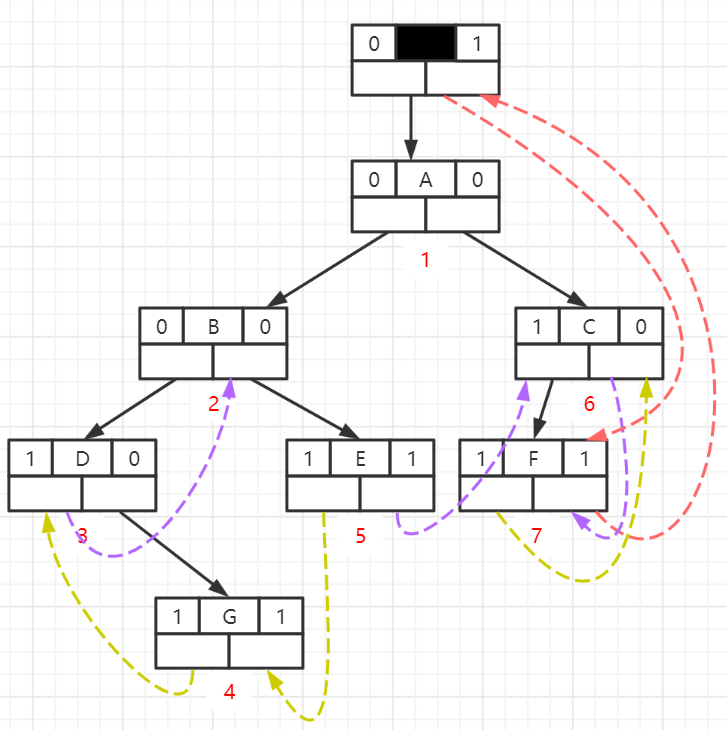
Postordinal Threaded Binary Tree

Code implementation (headless node)

void CreatePostThread(ThreadNode* t)
{
    if(t != NULL) PostThread(t); //A non-empty binary tree can be threaded, followed by a threaded binary tree
    if (pre->rchild == NULL) pre->rtag = 1; //Processing the last traversed node
}

void PostThread(ThreadNode* t) //Preorder traversal
{
    if (t != NULL) //Traversing when not an empty tree
    {
        PostThread(t->lchild); //Post-order traversal of left subtree
        PostThread(t->rchild); //Post-order traversal of right subtree
        visit(t); //Access Root Node
    }
}

void visit(ThreadNode* q)
{
    if (q->lchild == NULL) //Left subtree is empty, building precursor clues
    {
        q->lchild = pre;
        q->ltag = 1;
    }
    if (pre != NULL && pre->rchild == NULL)
    {
        pre->rchild = q; //Establishing a successor thread for a precursor node
        q->rtag = 1;
    }
    pre = q;
}

Program analysis

• Special attention should be paid to the dead-loop problem in the ordered-threaded binary tree, but not in the ordered and postordered-threaded binary trees.
• The code of a post-ordered threaded binary tree is basically the same as that of an ordered threaded binary tree, except that the middle-ordered traversal is about the root, and the second-ordered traversal is about the left-right root. In addition, in the sequential threaded binary tree, the last node needs to determine if its right child is NULL and if it is NULL, change ltag to 1. The ordered-threaded binary tree can be changed to 1 without judgment.

Code implementation (with header node)

void PostThread(ThreadNode*& p)
{
    PreThread(p->lchild);
    PreThread(p->rchild);
    if (p != NULL)
    {
        if (p->lchild == NULL)
        {
            p->lchild = pre;
            p->ltag = 1;
        }
        else p->ltag = 0;
        if (pre->rchild == NULL)
        {
            pre->rchild = p;
        }
    }
}

ThreadNode * CreatThread(ThreadNode *&t)
{
    ThreadNode* t, * root;
    root = (ThreadNode*)malloc(sizeof(ThreadNode)); //Create Head Node
    root->ltag = 0; //The lchild of the head node points to the left child (that is, to the root node)
    root->rtag = 1; //The rchild of the header node points to the thread (that is, to the last node visited during postsequential traversal)
    root->rchild = t; //The rchild of the first header node points to the root node
    if (t == NULL) root->lchild = pre; //When an empty binary tree is empty, the lchild of the head node points to itself
    else //Binary tree is not empty
    {
        root->lchild = t; //The lchild of the header node points to the root node
        pre = root; //pre is the precursor to node t for threading
        ThreadTree(t); //Post-order Traversal Threaded Binary Tree
        pre->rchild = root; //Finally, add a thread pointing to the head node
        pre->rtag = 1;
        t->rchild = pre; //Head Node Right Threaded
    }
    return root;
}

Program analysis

Finding a Precursor & Successor in a Cable Binary Tree

Finding a Precursor in an Ordered-Threaded Binary Tree

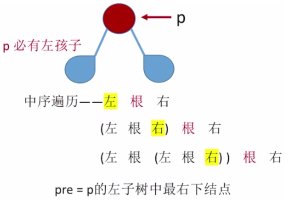
stay in order Line Cable two fork tree in look for reach finger set junction spot ∗ p Of in order Front drive p r e { ① if p − > l t a g = = 1 ， be p r e = p − > l c h i l d ② if p − > l t a g = = 0 ， be say bright p have to Yes Left Child son Find the intermediate precursor pre\begin{cases} of the specified node *p in the ordered threaded binary tree. If p->ltag==1, then pre = p->lchild \2 If p->ltag==0, P must have a left child \\end{cases} If p>ltag==1, then pre=p>lchild2. If p>ltag==0, then p must have a left child.

code implementation

ThreadNode* LastNode(ThreadNode* p) //Find the last node in the subtree rooted in P that was traversed in middle order
{
    while (p->ltag == 0) p = p->rchild; //Loop to find the rightmost lower node (not necessarily a leaf node)
    return p;
}

ThreadNode* PreNode(ThreadNode* p) //Finding the precursor node of node p in the ordered threaded binary tree
{
    if (p->ltag == 1) return p->lchild; //ltag=1 returns directly to the lead
    else return LastNode(p); //Lowest Right Node in Left Subtree
}

void RevInOrder(ThreadNode* t) //Reverse middle-order traversal of ordered threaded binary trees
{
    for (ThreadNode* p = LastNode(t); p != NULL; p = PreNode(p))
        printf("%c", p->data);
}

Find Successors in an Ordered-Threaded Binary Tree

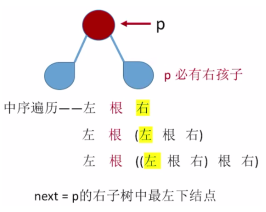
stay in order Line Cable two fork tree in look for reach finger set junction spot ∗ p Of in order after Following p r e { ① if p − > r t a g = = 1 ， be p r e = p − > r c h i l d ② if p − > r t a g = = 0 ， be say bright p have to Yes right Child son Find the intermediate sequence successor pre\begin{cases} of the specified node *p in the ordered threaded binary tree. If p->rtag==1, then pre = p->rchild \2 If p->rtag==0, P must have a right child\\end{cases} Finding the specified node P in the ordered threaded binary tree is followed by pre{1 if p>rtag==1 then pre=p>rchild 2 if p>rtag==0 then p must have a right child.

code implementation

ThreadNode* LastNode(ThreadNode* p) //Find the first node to be traversed in middle order in a P-rooted subtree
{
    while (p->ltag == 0) p = p->lchild; //Loop to find the leftmost lower node (not necessarily a leaf node)
    return p;
}

ThreadNode* NextNode(ThreadNode* p) //Finding successor nodes to node p in ordered threaded binary tree
{
    if (p->rtag == 1) return p->rchild; //ltag=1 returns directly to the next thread
    else return LastNode(p); //Lowest Left Node in Right Subtree
}

void RevInOrder(ThreadNode* t) //Reverse middle-order traversal of ordered threaded binary trees
{
    for (ThreadNode* p = LastNode(t); p != NULL; p = NextNode(p))
        printf("%c", p->data);
}

Find a pioneer in a sequential threaded binary tree

• ! It is not possible to find a precursor in a binary tree with a precursor thread. Because in a precedent traversal, the nodes in the left and right subtrees may only be successors of the roots, not precursors.
• There are two solutions:
  1. Traverse from scratch using soil method to define a *prepoint to the precursor node of the current node and *final point to the final precursor node to be found.
  (2) Add a pointer field parent to the list of 3-fork chains.

Analysis

if send use 3 fork chain surface ， be Yes four species can can Of feeling condition { ① p junction spot only Yes Left son tree ， no Yes right son tree ② p junction spot only Yes right son tree ， no Yes Left son tree ③ p junction spot as well as Yes Left son tree ， also Yes right son tree ④ p junction spot by root section spot If you use a 3-fork chain table, there are four possible cases \begin{cases} 1 p node has only a left subtree, no right subtree\2 p node has only a right subtree, and no left subtree\3 p node has both a left subtree and a right subtree\4 p node is a root node\\end{cases} If a 3-fork chain table is used, there are four possible scenarios: (1) p-node has only left subtree, no right subtree, (2) p-node has only right subtree, no left subtree, (3) p-node has both left subtree and right subtree, (4) p-node is root.

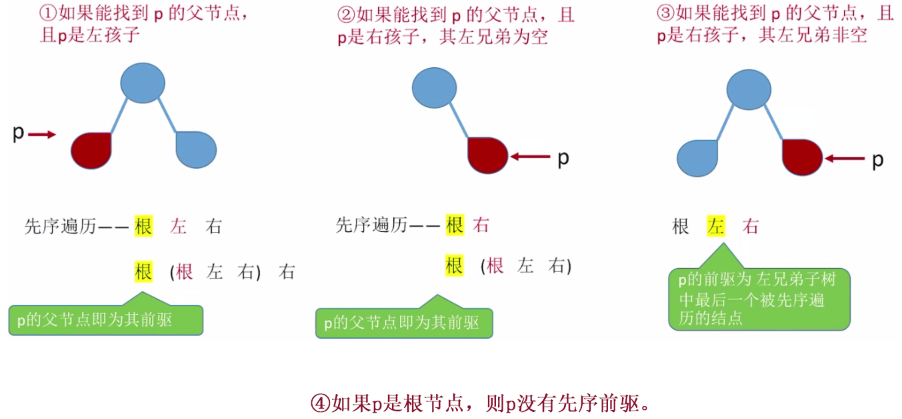
Find successors in a sequential threaded binary tree

Yes can can Of two species feeling condition { ① p junction spot Yes right Child son ， no Yes Left Child son ② p junction spot Yes right Child son ， also Yes Left Child son There are two possible scenarios \begin{cases}1 p node has a right child, no left child\2 p node has a right child, and there are left children\\end{cases} There are two possible scenarios {1)p node has right child, no left child, and P node has right child and left child.

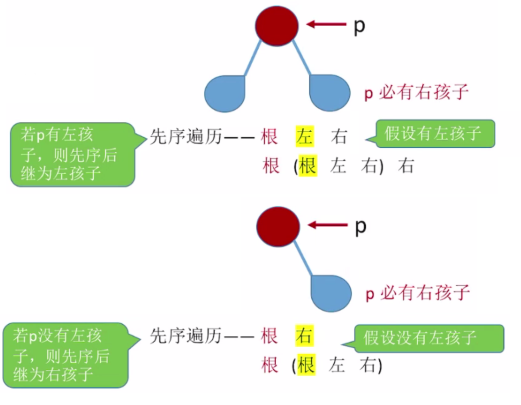
code implementation

ThreadNode* NextNode(ThreadNode* p) //Finding the successor nodes of node p in the sequential threaded binary tree
{
    if (p->rtag == 1) return p->rchild; //ltag=1 returns directly to the next thread
    else
    {
        if (p->ltag == 1) p->rchild; //If the p-node has no left child, the right child is its successor
        else return p->lchild; //p node has left child, left child is its successor node
    }
}

Finding a Precursor in a Postsequential Threaded Binary Tree

Yes can can Of two species feeling condition { ① p junction spot Yes Left Child son ， no Yes right Child son ② p junction spot Yes Left Child son ， also Yes right Child son There are two possible scenarios\begin{cases}1 p node has left children, no right children\2 p node has left children, and right children\\end{cases} There are two possible scenarios {1)p node has left children, no right children, and P node has left children and right children.

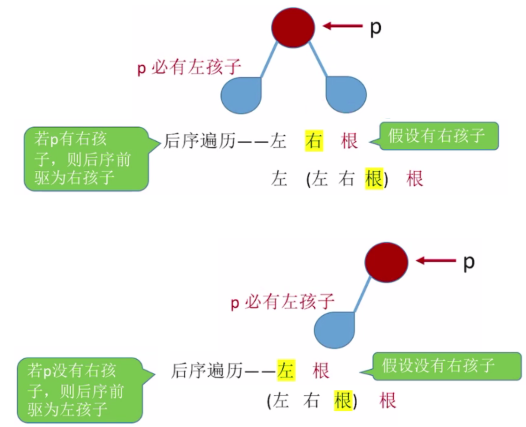
code implementation

ThreadNode* PreNode(ThreadNode* p) //Find the precursor node of node p in the sequential threaded binary tree
{
    if (p->ltag == 1) return p->lchild; //ltag=1 returns directly to the lead
    else
    {
        if (p->rtag == 1) p->rchild; //p node has a right child, then the right child is its successor
        else return p->lchild; //If the p-node has no right child, the left child is its successor
    }
}

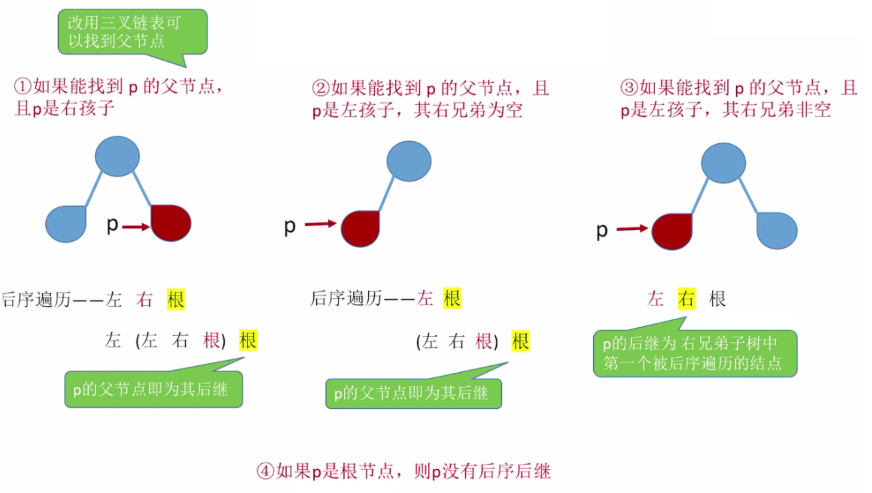
Finding Successors in a Successor-Threaded Binary Tree

• ! Successors in a sequential threaded binary tree cannot be found based on successor threads. Because in post-order traversal, nodes in left and right subtrees may only be precursors to the root, not successors.
• There are two solutions:
  1. Traverse from scratch using soil method to define a *pre point to the successor node of the current node and *final point to the successor node that is ultimately to be found.
  (2) Add a pointer field parent to the list of 3-fork chains.

Analysis

if send use 3 fork chain surface ， be Yes four species can can Of feeling condition { ① p junction spot Yes father section spot ， And p by father section spot Of right Child son ， p junction spot no Yes Left Child son ② p junction spot Yes father section spot ， And p by father section spot Of Left Child son ， p junction spot no Yes right Child son ③ p junction spot Yes father section spot ， And father section spot Yes Left , right Child son ④ p junction spot by root section spot If you use a 3-fork chain list, there are four possible scenarios \begin{cases} 1 P node has a parent node and P is the right child of the parent node, P node has no left child\2 P node has a parent node, P node has no right child\3 P node has a parent node, and the parent node has left and right children\ p node is the root node\casesend} If a 3-fork chain table is used, there are four possible situations: (1) p node has a parent node and p is the right child of the parent node, p node has no left child; (2) p node has a parent node and p is the left child of the parent node, p node has no right child; (3) p node has a parent node and p node has no right child; (3) p node has a parent node and the parent node has left and (4) p node is the root node.