tree
A tree of nonlinear structures in the logical structure of data
- Definition of tree (cycle definition):
(1) There is only one root node
(2) There are m disjoint trees except the root node, which are called subtrees. - Tree representation
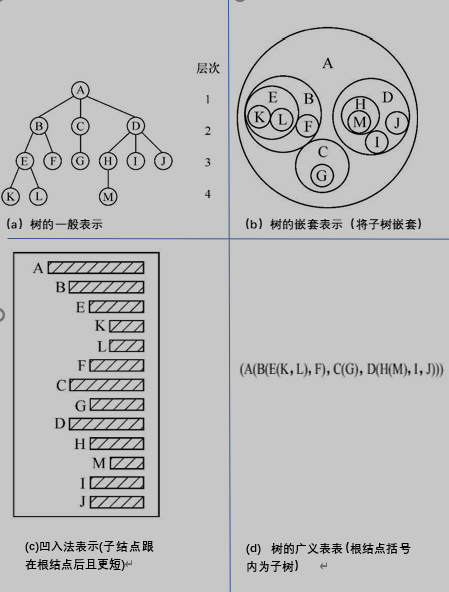
- Basic terms of trees
Node: an independent unit in a tree. Contains a data element and several branches to its subtree.
Degree of node: the number of subtrees owned by the node
Degree of tree: the maximum degree of each node in the tree
Leaf (terminal node): node with degree 0
Parents and children: the subtree of a node is called a child, and the corresponding node is called the child's parents
Brothers: the nodes of the same parents are called brothers
Ancestor: all nodes on the road from the root node to the change node (parents of parents.)
Descendant: corresponding to the ancestor, any node of all subtrees rooted from this node is called its descendant
Level: it is defined from the root. The root is the first level and the children of the root are the second level (similar to generation)
Cousins: same level
Tree depth: the maximum level of the tree
Forest: a collection of m disjoint trees
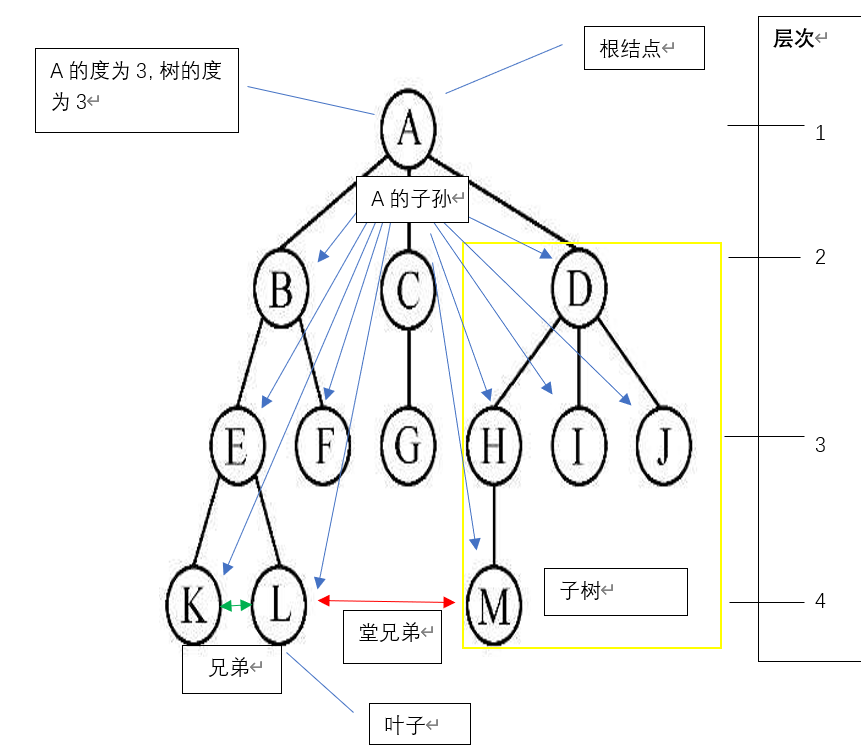
Binary tree
Binary tree is a special tree. The degree of the root node is at most 2. It is called left subtree and right subtree.
Basic knowledge of binary tree
- Properties of binary tree
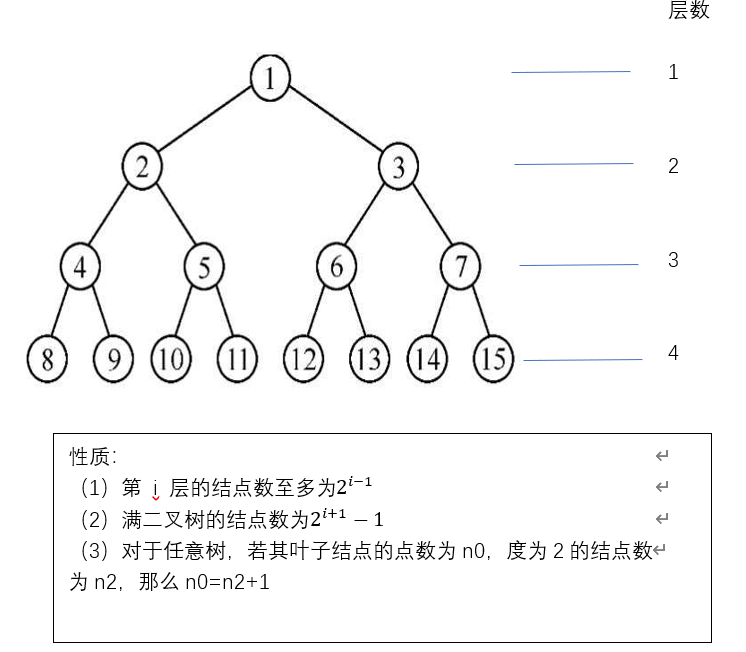
The corresponding relationship between nodes and children, parents, brothers and cousins. The sequence number is from the root node, from left to right.
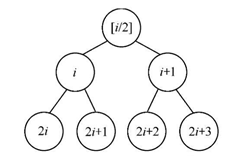
Proof of nature:
(1) According to the definition of binary tree, the degree of node is at most 2. If the first layer has a root node, then the second layer is 2 ^ 1. The conclusion is obtained by analogy
(2) The maximum number of nodes in each layer is known (full binary tree means that the number of nodes in each layer is the maximum)
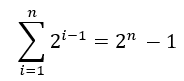
(3) Because the number of summary points n = N0 + N1 + N2 (the sum of knot points with degrees of 0, 1 and 2); It is also equal to the sum of the degrees corresponding to the root node and each node (if the degree of a node is 0, then its number of children is zero, if it is 1, then its number of children is 1, if it is 2, then the number of children is 2. The total number of children plus the root node) that is, n=1+n1+2*n2. The two formulas are equal, and the result is n0=n2+1
- Classification of binary tree
Full binary tree: the depth is k, and the number of nodes is 2^(i+1)-1 (the number of nodes in each layer of the binary tree is the maximum)
Complete binary tree: leaf nodes can only appear in the two layers with the largest number of layers (that is, if the maximum level of the offspring of its right branch is i, then the maximum level of its left subtree must be i+1)
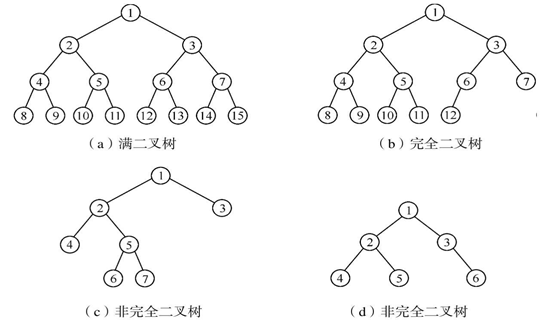
Storage structure of binary tree
1. Sequential storage
According to the sequence number of nodes in the tree, they are stored in an array. This storage method is only applicable to full binary trees.
#define MAX 100
//Data element (change the data element and modify the implementation of the basic element structure and interface)
typedef struct item {
//data item
int data;
bool operator==(const item& a) {
return data == a.data;
}
}Item;
typedef Item Btree[MAX];
Btree T;
2. Chain storage
According to the definition of binary tree, a node contains a data field, a left pointer (pointing to the left subtree) and a right pointer, and a pointer points to the root node.

#pragma once
#include<stdbool.h>
#include<stdio.h>
//Data element (change the data element and modify the implementation of the basic element structure and interface)
typedef struct item {
//data item
int data;
bool operator==(const item& a) {
return data == a.data;
}
}Item;
typedef struct node {
Item data;
struct node* Lnode, * Rnode;
}BTnode, * BTree;
Traversal of binary tree
theory
Traversing a binary tree is to patrol each node in the tree according to a search path, so that each node can be accessed only once. Its essence is to transform the tree of nonlinear structure into a linear sequence.
- Preorder traversal
(1) Operation: first traverse the root node, then traverse the left subtree, and finally the right subtree.
(2) The traversal result shown in the figure is A B C D E F G H
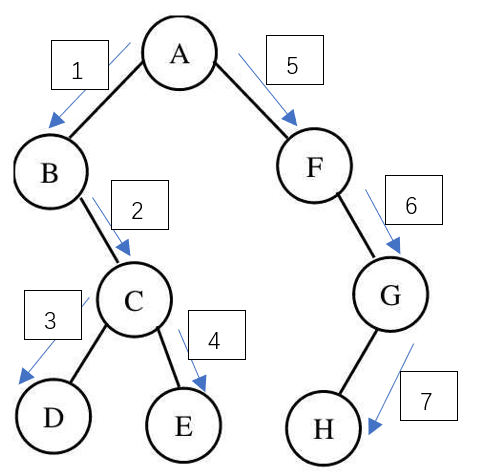
- Medium order traversal
(1) Operation: first traverse the left subtree, then the root node, and finally the right subtree.
(2) The traversal result shown in the figure is: B D C E A F H G
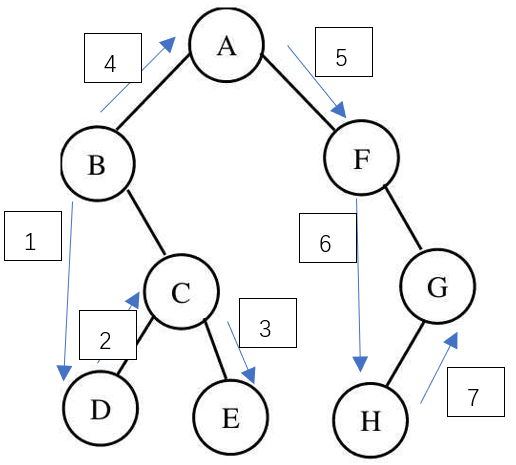
- Postorder traversal
(1) Operation: traverse the left subtree first, then the right subtree, and finally the root node
(2) As shown in the figure, the traversal result is D E C B H G F A
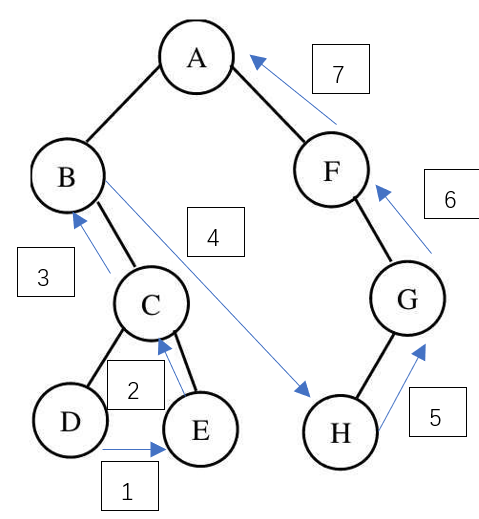
Note: a binary tree cannot be uniquely determined by preorder traversal and postorder traversal, because when there is only a left subtree (right subtree) for (left and right roots), it cannot be determined whether it is a left subtree or a right subtree according to the traversal results.
For example, the pre order and post order traversal results of the two trees in the figure below are the same.
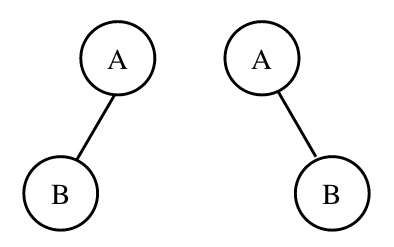
4. Level traversal
Start from the first layer and traverse from left to right
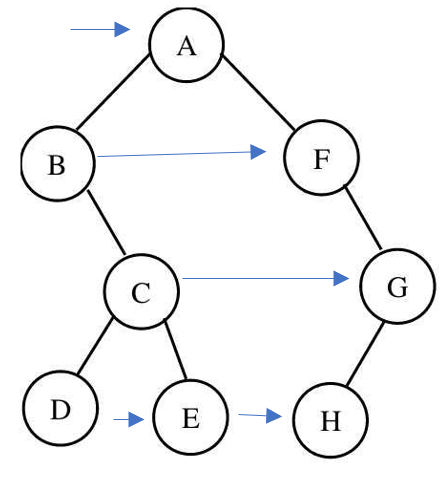
Implementation ideas and function code
The code implements medium order traversal, and there is little difference between pre order and post order.
- Recursive implementation of middle order traversal
According to the definition, the traversal operation is nested, so it is implemented by recursive algorithm.
If the rule of middle order traversal is left root right, then the left subtree and right subtree of the root node are regarded as trees with the left and right children of the root node as the root node and nested repeatedly.
//Recursive implementation of middle order traversal
void Inorder_traverse(BTree T) {
if (T) {
Inorder_traverse(T->Lnode);//Left subtree
T->Data.printf(); //The value of the output root
Inorder_traverse(T->Rnode);//Right subtree
}
}
- Non recursive implementation of middle order traversal
Non recursive implementation needs the data structure of stack. If necessary, you can check the stack knowledge in this column: Data structure_ Stack and queue.
//Non recursive implementation of middle order traversal
void Inorder_traverse1(BTree T) {
//Stack initialization
Lkstack S;
Lkstackinit(S);
BTree p = T;
BTnode* q = new BTnode; //Save backtracking point
while (p || S) {
if (p) { //The node is not empty and is stacked
Item e;
e.n = *p;
Push(S,e);
p = p->Lnode; //Left subtree until the left subtree is empty
}
else { //If the left subtree is empty, trace back its parent node and output it, and then traverse its right subtree
Item e;
Pop(S, e);
*q = e.n;
q->Data.printf(); Insert the code slice here
p = q->Rnode;
}
}
Lkstackfree(S);
}
- Implementation of hierarchical traversal
The implementation of hierarchical traversal requires the help of queues, and the relevant contents can be viewed: Data structure_ Stack and queue.
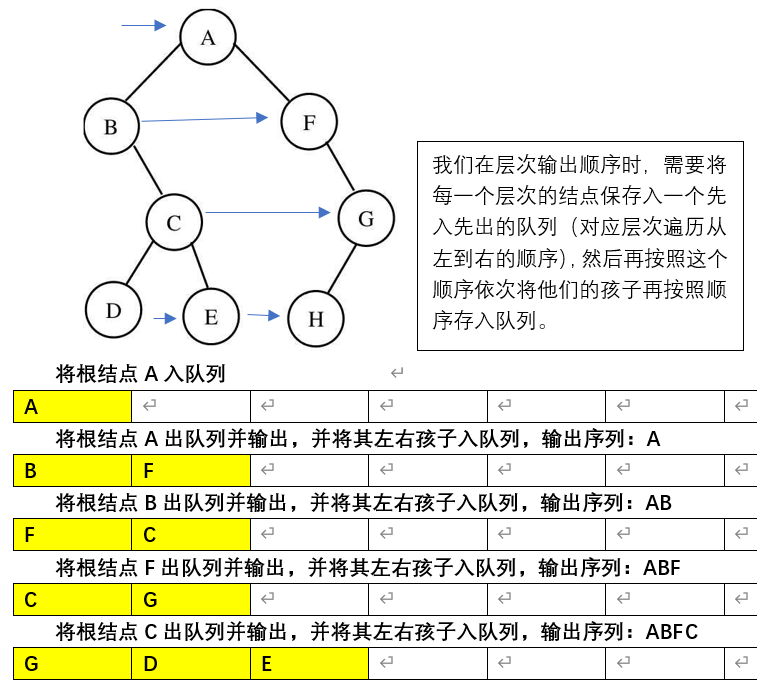
//level traversal
Cue of binary tree
theory
Previously, the chain storage structure of the binary tree storage structure knows that the right, left and right pointers of the binary tree point to the left and right children respectively. According to the nature, the number of nodes on the i-th layer of the full binary tree is 2^(i-1). If it is the last layer, all the left and right pointers of these nodes will be wasted. In order to make better use of resources, some useful information is stored in the empty left and right pointers (usually the front and rear drive nodes of the node traversing the sequence in the front, middle and rear order). These pointers to the front and back drive nodes are called clues, and the binary tree is called clue binary tree. The process of traversing the binary tree in some order to turn it into clue binary tree is called cueing.
code implementation
//Cueing
BTree pre=NULL;
void Inorder_threading(BTree T) {
if (T) {
Inorder_threading(T->Lnode); //Left subtree
if (!T->Lnode) {
T->Ltag = 1;
T->Lnode = pre;
}
else
T->Ltag = 0; //root
if (pre) {
if (!pre->Rnode) {
pre->Rtag = 1;
pre->Rnode = T;
}
else
pre->Rtag = 0;
}
pre = T;
Inorder_threading(T->Rnode); //Right subtree
}
}
//Traversal cued binary tree
void Inorder_threadBTree(const BTree T) {
BTree p = T;
while(p) {
while (p->Ltag == 0) //Traverse to the leftmost node
p = p->Lnode;
p->Data.printf();
while (p->Rtag == 1&& p->Rnode) { //After traversing the left subtree, the right subtree does not exist, and the successor node exists. Turn to the successor node.
p = p->Rnode; p->Data.printf();
}
//Right subtree exists
p = p->Rnode;
}
}
Complete code (binary tree traversal and clues)
code
Header file BTREE h
#pragma once
#include<stdbool.h>
#include<stdio.h>
#define MAX 100
//Binary tree data element (change the data element and modify the implementation of basic element structure and interface)
typedef struct item1 {
//data item
int data;
bool operator==(const item1& a) {
return data == a.data;
}
void printf() {
fprintf(stdout,"%c", data);
}
}Item1;
//Binary tree node
typedef struct node {
Item1 Data;
struct node* Lnode, * Rnode;
int Ltag, Rtag;
}BTnode, * BTree;
///
///Implementation of stack
///
//Stack data element (change the data element and modify the implementation of basic element structure and interface)
typedef struct item {
//data item
BTnode n;
bool operator==(const item& a) {
return n.Data.data == a.n.Data.data;
}
void printf() {
fprintf(stdout, "%c", n.Data.data);
}
}Item;
typedef struct Stack {
Item e;
struct Stack* next;
}Stack, * Lkstack;
//Stack initialization
bool Lkstackinit(Lkstack& L);
//Push
bool Push(Lkstack& L, Item e);
//Out of stack
bool Pop(Lkstack& L, Item& e);
//Stack value
bool GetItem(const Lkstack L, Item& e);
///
///Implementation of queue
///
///
typedef struct {
Item* base;
int front;
int rear;
}Queue;
//initialization
bool QueueInit(Queue& q);
//Find queue length
int Queuelen(const Queue q);
//Join the team
bool QueueEn(Queue& q, Item e);
//Out of the team
bool QueueOut(Queue& q, Item& e);
//Header element
bool GetItem(const Queue q, Item& e);
Main function
#include<stdio.h>
#include<stdlib.h>
#include"Btree.h"
///--------------------------------------------
///Interface implementation of stack operation
/// -------------------------------------------
//Stack initialization
bool Lkstackinit(Lkstack& L) {
L = NULL;
return true;
}
//Push
bool Push(Lkstack& L, Item e) {
Lkstack p = new Stack;
p->e = e;
p->next = L;
L = p;
return true;
}
//Out of stack
bool Pop(Lkstack& L, Item& e) {
if (!L)
return false;
e = L->e;
Lkstack p = L;
L = L->next;
delete p;
return true;
}
//Stack value
bool GetItem(const Lkstack L, Item& e) {
if (!L)
return false;
e = L->e;
return true;
}
//Stack release
void Lkstackfree(Lkstack& L) {
Lkstack p = NULL;
while (L) {
p = L->next;
delete L;
L = p;
}
}
///--------------------------------------------
///Queue operation implementation interface
/// -------------------------------------------
//initialization
bool QueueInit(Queue& q) {
q.base = new Item[MAX];
if (!q.base)
return false;
q.front = q.rear = 0;
return true;
}
//Find queue length
int Queuelen(const Queue q) {
return (q.rear-q.front)%MAX;
}
//Join the team
bool QueueEn(Queue& q, Item e) {
if ((q.rear + 1) % MAX == q.front)
return false;
q.base[q.rear] = e;
q.rear = (q.rear + 1) % MAX;
return true;
}
//Out of the team
bool QueueOut(Queue& q, Item& e) {
if (q.front==q.rear)
return false;
e=q.base[q.front];
q.front = (q.front + 1) % MAX;
return true;
}
//Header element
bool GetItem(const Queue q, Item& e) {
if (q.front == q.rear)
return false;
e = q.base[q.front];
return true;
}
//Release queue
void Sqqueuefree(Queue& q) {
if (q.base) {
free(q.base);
}
}
///--------------------------------------------
///Traversal operation
/// -------------------------------------------
//Traversing the creation tree in sequence
//printf("please enter the binary tree sequence traversed by the previous sequence: ('#' is empty) \ n");
void Creat_BTree(BTree &T) {
char ch;
ch = getchar();
if (ch == '#') T = NULL;
else if (ch == '\n');
else {
T = new BTnode;
T->Data.data = ch;
Creat_BTree(T->Lnode);
Creat_BTree(T->Rnode);
}
}
//Recursive implementation of preorder traversal
void Forder_traverse(const BTree T) {
if (T) {
T->Data.printf();
Forder_traverse(T->Lnode);
Forder_traverse(T->Rnode);
}
}
//Recursive implementation of middle order traversal
void Inorder_traverse(const BTree T) {
if (T) {
Inorder_traverse(T->Lnode);
T->Data.printf();
Inorder_traverse(T->Rnode);
}
}
//Non recursive implementation of middle order traversal
void Inorder_traverse1(const BTree T) {
Lkstack S;
Lkstackinit(S);
BTree p = T;
BTnode* q = new BTnode;
while (p || S) {
if (p) {
Item e;
e.n = *p;
Push(S,e);
p = p->Lnode;
}
else {
Item e;
Pop(S, e);
*q = e.n;
q->Data.printf();
p = q->Rnode;
}
}
Lkstackfree(S);
}
//Recursive implementation of post order traversal
void Rorder_traverse(const BTree T) {
if (T) {
Rorder_traverse(T->Lnode);
Rorder_traverse(T->Rnode);
T->Data.printf();
}
}
//level traversal
void level_traverse(const BTree T) {
Queue q; // Queue initialization
QueueInit(q);
if (T != NULL) { //Root node in queue
Item e1;
e1.n = *T;
QueueEn(q, e1);
Item e;
while (QueueOut(q, e)) { //Nodes out of the queue and add left and right children to the queue
BTree p = new BTnode;
*p = e.n;
p->Data.printf();
if (p->Lnode != NULL) {
Item e;
e.n = *(p->Lnode);
QueueEn(q, e);
}
if (p->Rnode != NULL) {
Item e;
e.n = *(p->Rnode);
QueueEn(q, e);
}
free(p);
}
}
Sqqueuefree(q);
}
///--------------------------------------------
///Clue binary tree
/// -------------------------------------------
//Cueing
BTree pre=NULL;
void Inorder_threading(BTree T) {
if (T) {
Inorder_threading(T->Lnode); //Left subtree
if (!T->Lnode) {
T->Ltag = 1;
T->Lnode = pre;
}
else
T->Ltag = 0; //root
if (pre) {
if (!pre->Rnode) {
pre->Rtag = 1;
pre->Rnode = T;
}
else
pre->Rtag = 0;
}
pre = T;
Inorder_threading(T->Rnode); //Right subtree
}
}
//Traversal cued binary tree
void Inorder_threadBTree(const BTree T) {
BTree p = T;
while(p) {
while (p->Ltag == 0)
p = p->Lnode;
p->Data.printf();
while (p->Rtag == 1&& p->Rnode) {
p = p->Rnode; p->Data.printf();
}
p = p->Rnode;
}
}
int main(int argc, char argv[]) {
BTree T;
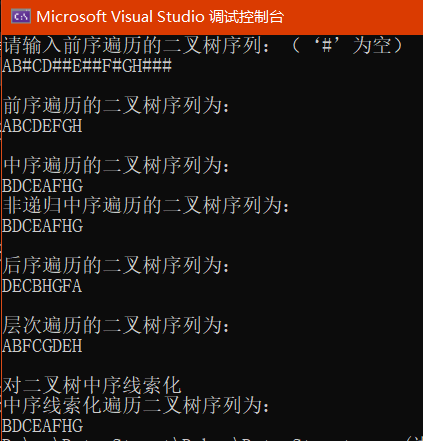
printf("Please enter the binary tree sequence traversed by the preamble:('#’Empty) \ n "");
Creat_BTree(T);
printf("\n The binary tree sequence traversed by the preamble is:\n");
Forder_traverse(T);
printf("\n\n The binary tree sequence traversed in the middle order is:\n");
Inorder_traverse(T);
printf("\n The binary tree sequence traversed in non recursive middle order is:\n");
Inorder_traverse1(T);
printf("\n\n The binary tree sequence traversed in the post order is:\n");
Rorder_traverse(T);
printf("\n\n The binary tree sequence traversed by the hierarchy is:\n");
level_traverse(T);
printf("\n\n Order cueing in binary tree");
Inorder_threading(T);
printf("\n The sequence of medium order threaded traversal binary tree is:\n");
Inorder_threadBTree(T);
return 0;
}
Running screenshot