Pre comparable interface

java provides an interface. Comparable is used to define sorting rules. There is an abstract method in the interface to implement comparison rules.

package comparable;
/*
    Define the Test class Test, and define the Test method Comparable getMax(Comparable c1, Comparable c2) in the Test class Test to complete the Test
 */
public class Comparable1 {

    public static void main(String[] args) {
        student s1 = new student("Zhang San",18);
        student s2 = new student("Li Si",20);


        Comparable max = getMax(s1,s2);
        System.out.println(max);
    }



    public static Comparable getMax(Comparable c1,Comparable c2){  // It is equivalent to polymorphism. On the left is the interface and on the right is the implementation class object



        int result = c1.compareTo(c2);
        if (result>=0){
            return c1;
        }else{
            return c2;
        }



    }

}

package comparable;

import javax.print.DocFlavor;
/*
    Define a student class with two attributes: age and name username, and provide comparison rules through the Comparable interface
 */
public class student implements Comparable<student>{

    private String name;
    private int age;

    public student() {
    }

    public student(String name, int age) {
        this.name = name;
        this.age = age;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public int getAge() {
        return age;
    }

    public void setAge(int age) {
        this.age = age;
    }

    @Override
    public String toString() {
        return "student{" +
                "name='" + name + '\'' +
                ", age=" + age +
                '}';
    }

    @Override
    public int compareTo(student o) {

        return this.getAge()-o.getAge();
    }
}

1, Simple sort

1. Bubble sorting

1.1 code implementation

package bubble;

import java.util.Arrays;

public class BubbleTest {
    public static void main(String[] args) {
        Integer[] arr = {4,5,6,3,2,1};
        Bubble1.sort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

package bubble;

import java.util.Comparator;

public class Bubble1 {
    /*
        Sorts the elements in the array
     */
    public static void sort(Comparable[] a ){
        for (int i=a.length-1;i>0;i--){    //Determine the number of bubbling elements each time, and put the largest element at the largest index each time, so subtract 1 each time
            for (int j=0;j<i;j++){         //Compare the size of two adjacent elements each time and exchange positions
                //Compare the values at index j and index j+1
                if (greater(a[j],a[j+1])){
                    exch(a,j,j+1);
                }
            }
        }


    }

    /*
        Compare whether the element is larger than the w element
     */
    private static boolean greater(Comparable v, Comparable w){
        return v.compareTo(w)>0;
    }

    /*
        Array elements i and j swap positions
     */
    private static void exch(Comparable[] a,int i, int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

1.2 complexity analysis

The bubbling loop uses a double-layer for loop, in which the inner loop body is the code that really completes the sorting. Therefore, we analyze the time complexity of bubbling sorting, mainly analyzing the execution times of the inner loop body.
In the worst case, the element to be sorted is {6, 5, 4, 3, 2, 1}, then:
The number of element comparisons is:
(N-1)+(N-2)+(N-3)+...+2+1 = ((N-1)+1)(N-1)/2=N^2/2-N/2
The number of element exchanges is:
(N-1)+(N-2)+(N-3)+...+2+1 = ((N-1)+1)(N-1)/2=N^2/2-N/2
Total execution times:
N ^ 2 /2-N/2 + N^2/2-N/2 = N ^ 2 -N

Derivation rule of big O: time complexity is O(N^2)

2. Select Sorting

2.1 sorting principle

• During each traversal, it is assumed that the element at the first index is the minimum value, which is compared with the values at other indexes in turn. If the value at the current index is greater than the value at some other index, it is assumed that the value at some other index is the minimum value, and finally the index where the minimum value is located can be found
• Swap the values at the index where the first index and the minimum value are located

2.2 code implementation

• Select minimum value

package select;

import java.util.Arrays;

public class SelectTest {
    public static void main(String[] args) {
        //raw data
        Integer[] a = {4,6,8,7,9,2,10,1};
        Select1.sort(a);
        System.out.println(Arrays.toString(a));


    }
}

package select;

public class Select1 {

    public static void sort(Comparable[] a){
        for(int i=0;i<a.length-2;i++){
            int minIndex = i;
            for (int j=i+1;j<a.length;j++){
                //You need to compare the value at the minimum index minIndex with the value at the j index
                if (greater(a[minIndex],a[j])){
                    minIndex=j;
                }
            }
            //Swap the value at index minIndex where the smallest element is located and the value at index i
            exch(a,i,minIndex);

        }
    }

    /*
    Compare whether the element is larger than the w element
 */
    private static boolean greater(Comparable v, Comparable w){
        return v.compareTo(w)>0;
    }

    /*
        Array elements i and j swap positions
     */
    private static void exch(Comparable[] a,int i, int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

• Select maximum value

package sort;

public class Select {

    private static Comparable[] assist;

    public static boolean greater(Comparable v, Comparable w){
        return v.compareTo(w)>0;
    }
    /*
    Array elements i and j swap positions
     */
    private static void exch(Comparable[] a,int i, int j){
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }
    public static void sort(Comparable[] a){
        assist = new Comparable[a.length];
        for (int i=a.length-1; i>0; i--){
            int maxindex = i;
            for (int j=0; j<i; j++){
                if (greater(a[j],a[maxindex])){
                    maxindex = j;
                }
            }

            exch(a,i,maxindex);




        }
    }
}

package test;

import sort.Select;

import java.util.Arrays;

public class SelectTest {
    public static void main(String[] args) {
        Integer[] a = {4,5,6,3,2,1};
        Select.sort(a);
        System.out.println(Arrays.toString(a));
    }
}

2.3 complexity analysis

The selection sorting uses a double-layer for loop, in which the outer loop completes data exchange and the inner loop completes data comparison, so we count the times of data exchange and data comparison respectively:
Data comparison times:
(N-1)+(N-2)+(N-3)+...+2+1 = ((N-1)+1)*(N-1)/2=N^2/2-N/2
Data exchange times:
N-1
Time complexity:
N^2/2-N/2+N-1
Large complexity: O(N^2)

3. Insert sort

3.1 sorting principle

• Divide all elements into two groups, sorted and unordered
• Find the first element in the unordered group and insert it into the sorted group
• The flashback traverses the sorted elements and compares them with the inserted elements until one element is found to be smaller than the element to be inserted, then the element to be inserted is placed in this position, and the other elements are moved back one bit

3.2 code implementation

package insertion;

import java.util.Arrays;

public class InnsertionTest {
    public static void main(String[] args) {
        Integer[] a = {4,3,2,10,12,1,5,6};

        Insertion1.sort(a);

        System.out.println(Arrays.toString(a));
    }
}

package insertion;

public class Insertion1 {


    /*
        Sort the elements in array a
     */
    public static void sort(Comparable[] a)
    {
        for(int i=1;i<a.length;i++){

            for(int j=i;j>0;j--){
                //Compare the value at index with the value at index-1. If the value at index j-1 is larger than the value at index j, if not, find the appropriate position and exit the loop
                if (greater(a[j-1],a[j])){
                    exch(a,j-1,j);
                }else{
                    break;
                }
            }
        }
    }

    /*
Compare whether the element is larger than the w element
*/
    private static boolean greater(Comparable v, Comparable w){
        return v.compareTo(w)>0;
    }

    /*
        Array elements i and j swap positions
     */
    private static void exch(Comparable[] a,int i, int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

3.3 time complexity analysis

Worst case: [12, 10, 6, 5, 3, 2, 1]

Number of comparisons:
(N-1)+(N-2)+(N-3)+...+2+1 = ((N-1)+1)*(N-1)/2=N^2/2-N/2

Number of exchanges:
(N-1)+(N-2)+(N-3)+...+2+1 = ((N-1)+1)*(N-1)/2=N^2/2-N/2

Total execution times:
N ^ 2 /2-N/2 + N^2/2-N/2 = N ^ 2 -N
Big O derivation rule: O(N^2)

2, Advanced sorting

The complexity of simple sorting is O(N^2), which is not suitable for large-scale input

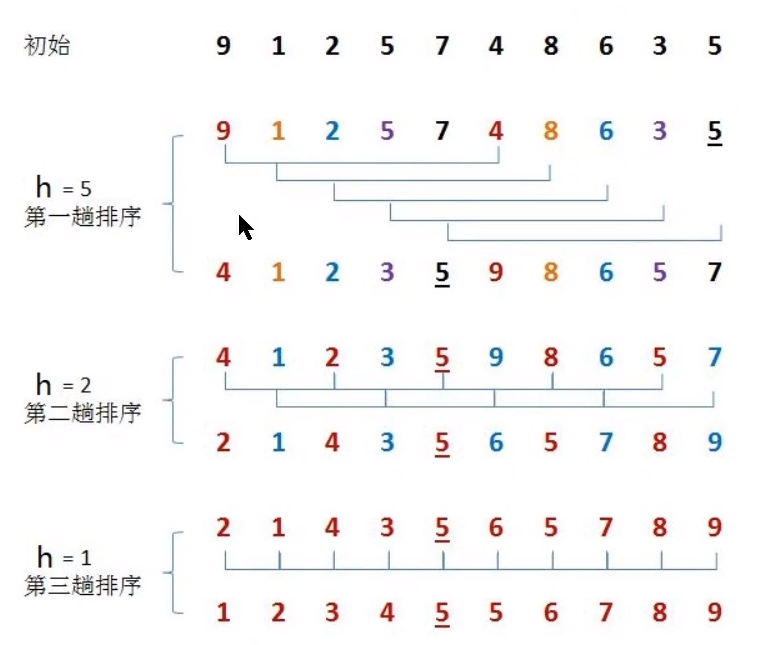
1. Hill sort

1.1 sorting principle

• Select a growth amount h and group the data according to the growth amount h as the basis for data grouping
• Insert and sort each group of data divided into groups
• Reduce the growth to 1 and repeat the second step
• Determination of h
• understand
  Hill sort is to use different h to group the original array in different forms. For each h, the original array can be divided into several different groups. The starting point of each group is to increase from each index of H to the length-1 index.

int h = 1;
while(h<length/2){
h = 2*h+1; 
}

//Reduction rule of h
 h = h/2;

1.2 code implementation

package shell;

import java.util.Arrays;

public class ShellTest {
    public static void main(String[] args) {
        Integer[] a = {9,1,2,5,7,4,8,6,3,5};
        Shell1.sort(a);
        System.out.println(Arrays.toString(a));
    }


}

package shell;

public class Shell1 {

    /*
        Sort the elements in array a
     */

    public static void sort(Comparable[] a){
        //Determine h value
        int h = 1;
        while(h<a.length/2){
            h=2*h+1;
        }
        //Shell Sort 
        while(h>=1){
            //Determine the elements to be sorted
            for(int i=h;i<a.length;i++){
                //The elements to be sorted are inserted and sorted under the current group
                /*
                    At first, i thought that the following loop was useless. Just use the values at the i and i-h indexes to judge?
                    In this way, only the values at I and i-h are exchanged, and the values at I and i-2h are not compared and exchanged
                    Therefore, this inner loop controls the grouping. When i and h are determined, each execution of this inner loop is to execute the insertion sorting of the [group corresponding to each i]
                    Because it involves the comparison of a[j] and a[j-h], J > = H
                 */
                for (int j = i; j>=h;j-=h){
                    if (greater(a[j-h],a[j])){
                        exch(a,j-h,j);
                    }else{
                        break;
                    }
                }
            }


            //Decrease the value of h
            h = h/2;
        }

    }

    /*
   Compare whether the element is larger than the w element
*/
    private static boolean greater(Comparable v, Comparable w){
        return v.compareTo(w)>0;
    }

    /*
        Array elements i and j swap positions
     */
    private static void exch(Comparable[] a,int i, int j){
        Comparable temp;
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

1.3 time complexity analysis

Prior analysis, more complex. The use of ex post complexity.

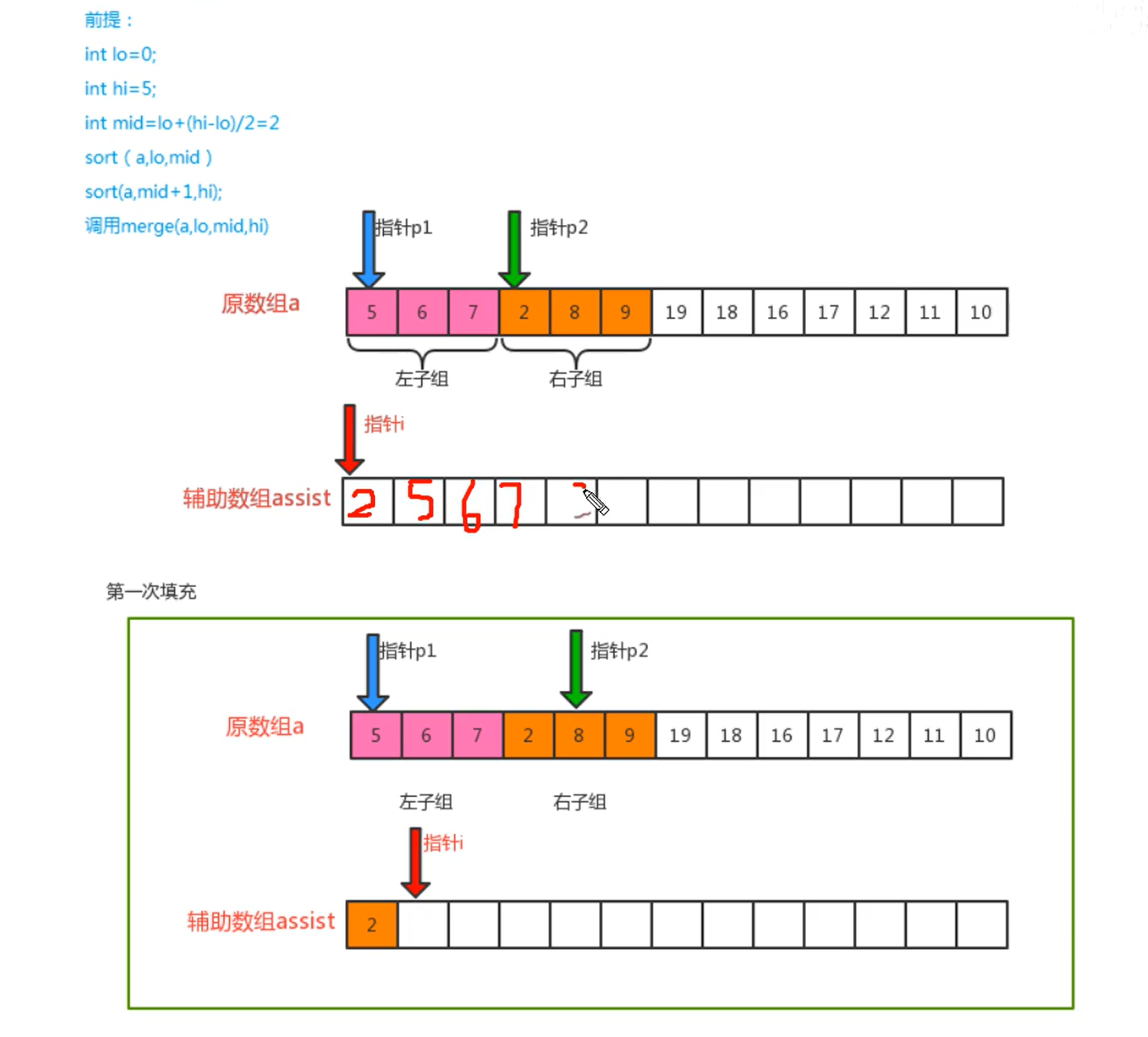
2. Merge and sort

2.1 sorting principle

• As far as possible, divide a group of data into two subgroups with equal elements, and continue to split each subgroup until the number of elements in each subgroup is 1.
• Merge two adjacent subgroups into an ordered large group
• Repeat step 2 until there is only one group in the end
  
• Principle of merging and sorting:
  
  
  
  

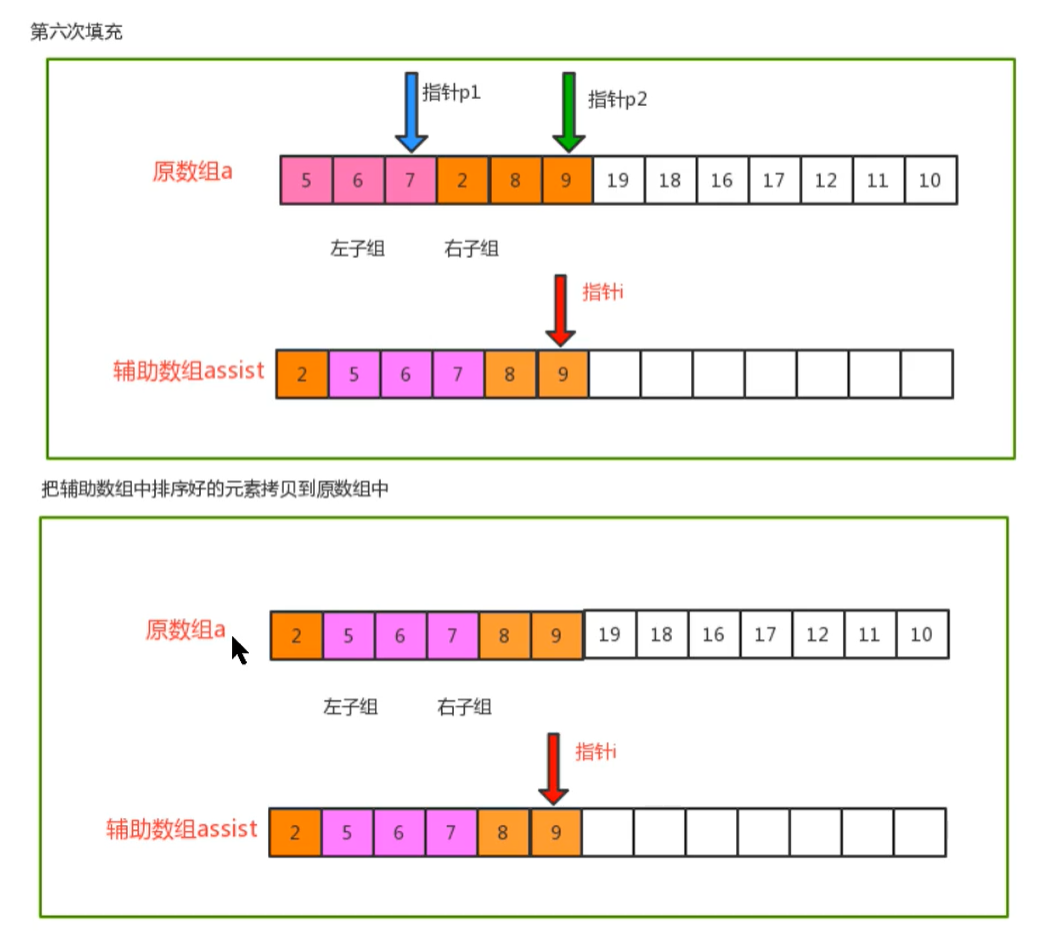
2.2 code implementation

package merge;

public class Merge1 {
    //Auxiliary array required for merging
    private static Comparable[] assist;
    /*
        Compare whether the element is smaller than the w element
     */
    private static boolean less(Comparable v, Comparable w){
        return v.compareTo(w)<0;
    }

    /*
        Array elements i and j swap positions
     */
    private static void exch(Comparable[] a,int i, int j){
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }


    /*
        Sort the elements in array a
     */
    public static void sort(Comparable[] a){
        //Initialize auxiliary array assist
        assist = new Comparable[a.length];
        //Define a lo variable and a hi variable to record the minimum index and the maximum index in the array respectively
        int lo = 0;
        int hi = a.length-1;
        //Call the sort overloaded method to sort the elements in array a from index lo to index hi
        sort(a,lo,hi);
    }

    /*
        Sort the elements from lo to hi in array a
     */
    private static void sort(Comparable[] a, int lo, int hi){
        //Do security testing to ensure that the iteration can end
        if(hi<=lo){
            return;
        }
        //The data between lo and hi are divided into two groups
        int mid = lo+(hi-lo)/2;

        //Sort the data of each group separately
        /*
            This sort recursively splits an array until the smallest subgroup starts to return,
            Return to the subgroup of the penultimate layer, and then split the right subgroup of the subgroup of the penultimate layer (1 element),
            Continue to return to the subgroup of the penultimate layer, and merge and sort at this time. After the penultimate level sorting is completed, return upward, and so on to complete the sorting.
         */
        sort(a, lo, mid);
        sort(a,mid+1,hi);

        merge(a,lo,mid,hi);




    }

    //Then merge the data in the two groups (sort in the merging process)
    private static void merge(Comparable[] a, int lo, int mid, int hi){

        //Define 3 pointers
        int i = lo;
        int p1 = lo;
        int p2 = mid+1;

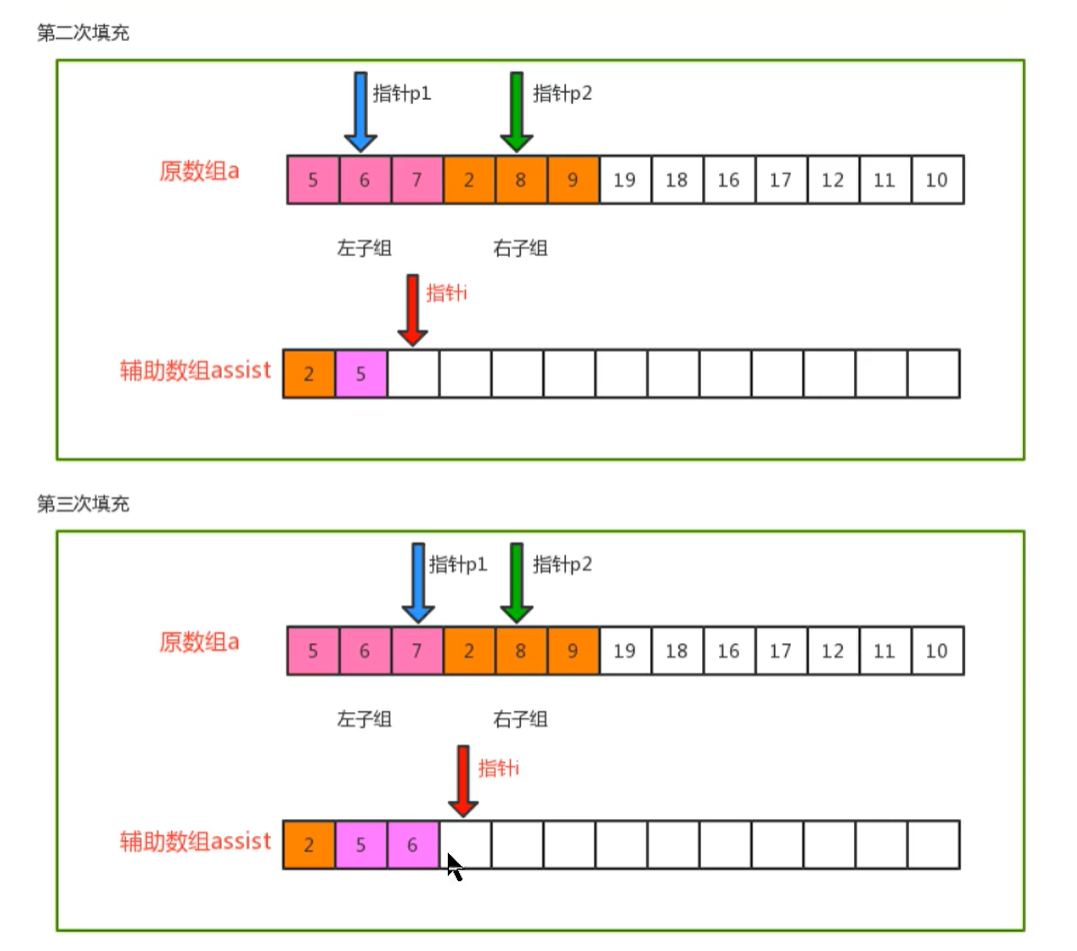
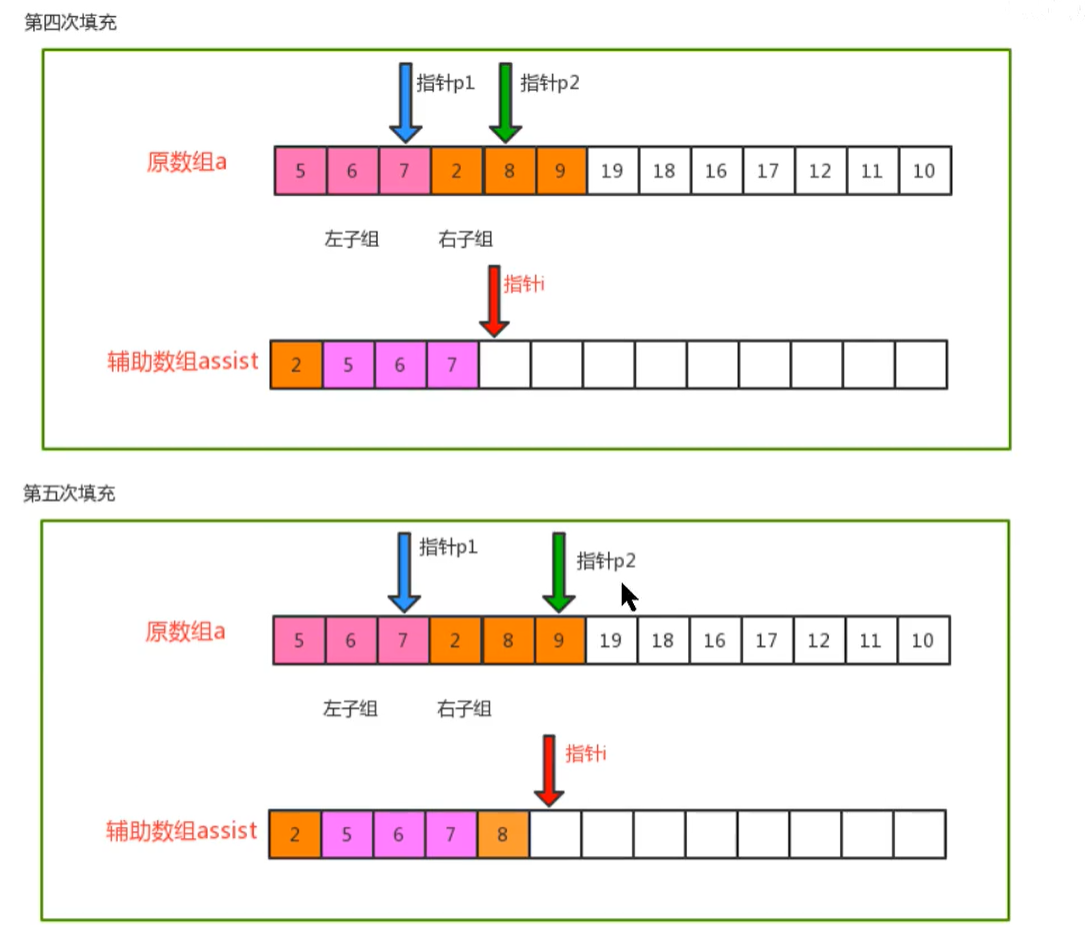
        //Traverse, move the pointers p1 and p2, compare the corresponding values, find the smallest one, and put it at the corresponding index of the auxiliary array
        while(p1<=mid && p2<=hi){
            if (less(a[p1],a[p2])){
                assist[i++] = a[p1++];
            }else{
                assist[i++] = a[p2++];
            }

        }

        //Traversal. If the p1 pointer is not completed, move the p1 pointer in sequence and put the corresponding elements at the index of the auxiliary array
        while (p1<=mid){
            assist[i++] = a[p1++];
        }
        //Traversal. If the p2 pointer is not completed, move the p1 pointer in sequence and put the corresponding element at the index of the auxiliary array
        while (p2<=hi){
            assist[i++] = a[p2++];
        }

        //Copy the elements in the auxiliary array to the original array
        for (int index = lo; index<=hi; index++){
            a[index] = assist[index];
        }

    }
}

package merge;

import java.lang.reflect.Array;
import java.util.Arrays;

public class MergeTEst {
    public static void main(String[] args) {
        Integer[] a = {66,9,8,4,5,7,1,3,6,2};
        Merge1.sort(a);
        System.out.println(Arrays.toString(a));

    }
}

2.3 complexity analysis

Regardless of recursion, i look at each layer of the binary tree. For the subarray of each layer, the worst comparison is that the pointer of each subarray traverses all the elements of the array, that is, n (compared n times); and the depth of the binary tree is l o g 2 n log_2^n log2n} layer, so the time complexity of merging and sorting is O ( n l o g n ) O(nlogn) O(nlogn)

3. Quick sort

3.1 sorting principle

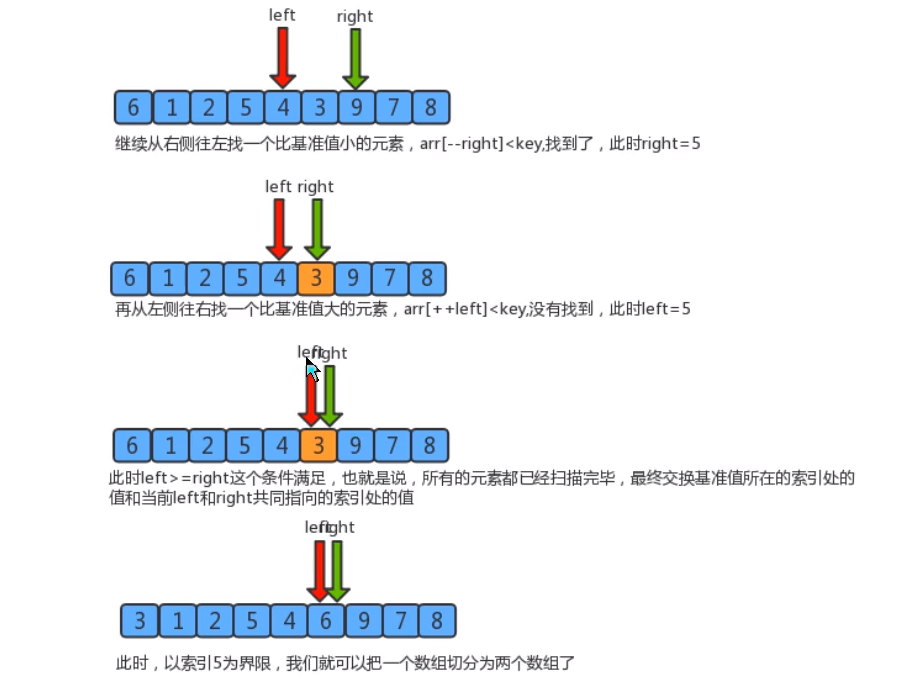
• First, set a boundary value, and divide the array into left and right parts through the boundary value
• Put the data greater than or equal to the boundary value to the right of the array, and the array less than the boundary value to the left of the array. At this time, all elements in the left part are less than or equal to the boundary value, while all elements in the right part are greater than or equal to the boundary value
• Then, the data on the left and right can be sorted independently. For the array data on the left, you can take a boundary value and divide this part of the data into left and right parts. Similarly, place a smaller value on the left and a larger value on the right. The array data on the right can also be processed similarly.
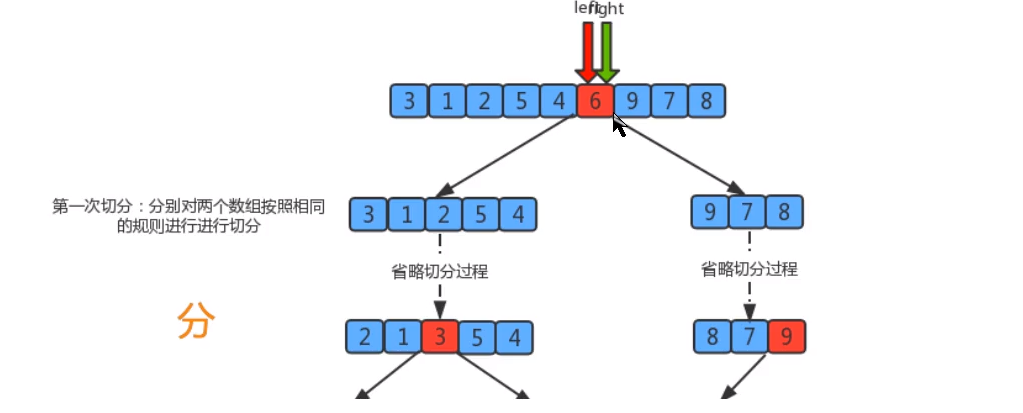
• By repeating the above process, we can see that this is a recursive definition. The left part is sorted recursively, and then the right part is sorted recursively. When the left and right parts of the data are sorted, the whole array is sorted.
  

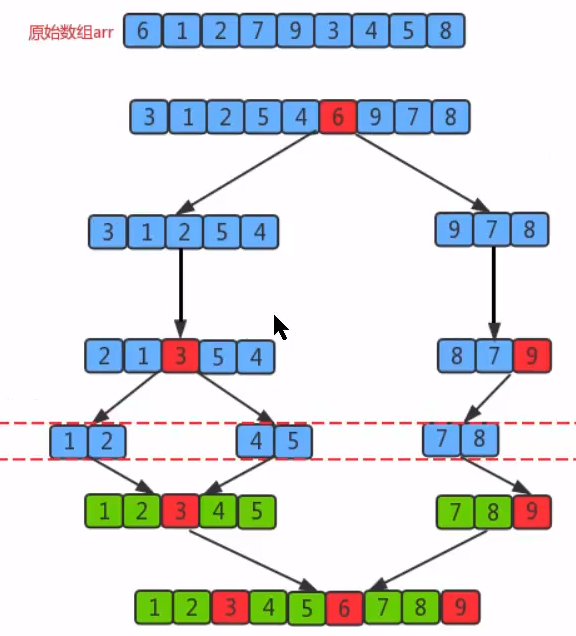
Segmentation principle

2.2 code implementation

package quick;

public class Quick1 {
    /*
        Compare whether the v element is smaller than the w element
     */
    private static boolean less(Comparable v, Comparable w){
        return v.compareTo(w)<0;
    }

    /*
        Data element i and data element j are exchanged
     */
    private static void exch(Comparable[] a, int i, int j){
        Comparable t=a[i];
        a[i] = a[j];
        a[j] = t;
    }

    /*
        Sort the elements in the array
     */
    public static void sort(Comparable[] a){
        int lo = 0;
        int hi = a.length-1;

        sort(a,lo,hi);

    }

    /*
        Sort the elements in array a from index lo to index hi
     */
    private static void sort(Comparable[] a, int lo, int hi){
        //Security detection
        if (lo>=hi){
            return;
        }

        //Perform segmentation to obtain the index at the segmentation
        int partition = partition(a,lo,hi);

        //Continue to segment and group the obtained left subgroup
        sort(a,lo,partition-1);
        sort(a,partition+1,hi);

    }

    /*
        Group the elements in array a from index lo to index hi, and return the index corresponding to the grouping boundary
     */
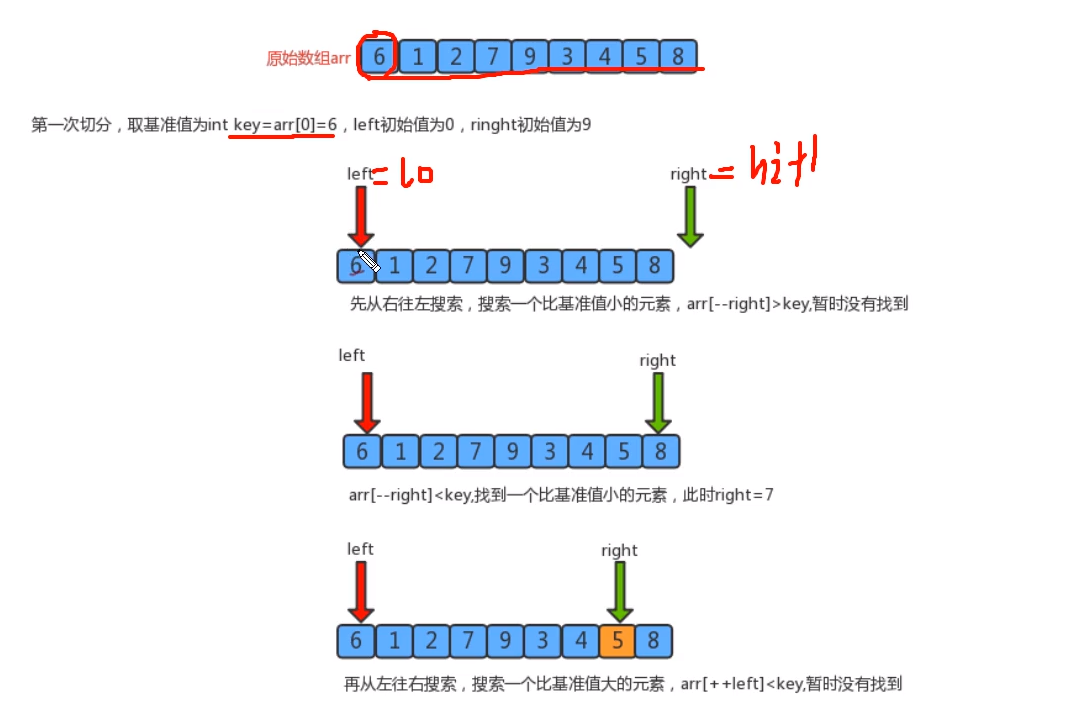
    public static int partition(Comparable[] a ,int lo, int hi){

        int left = lo;
        int right = hi+1;
        int key = lo;
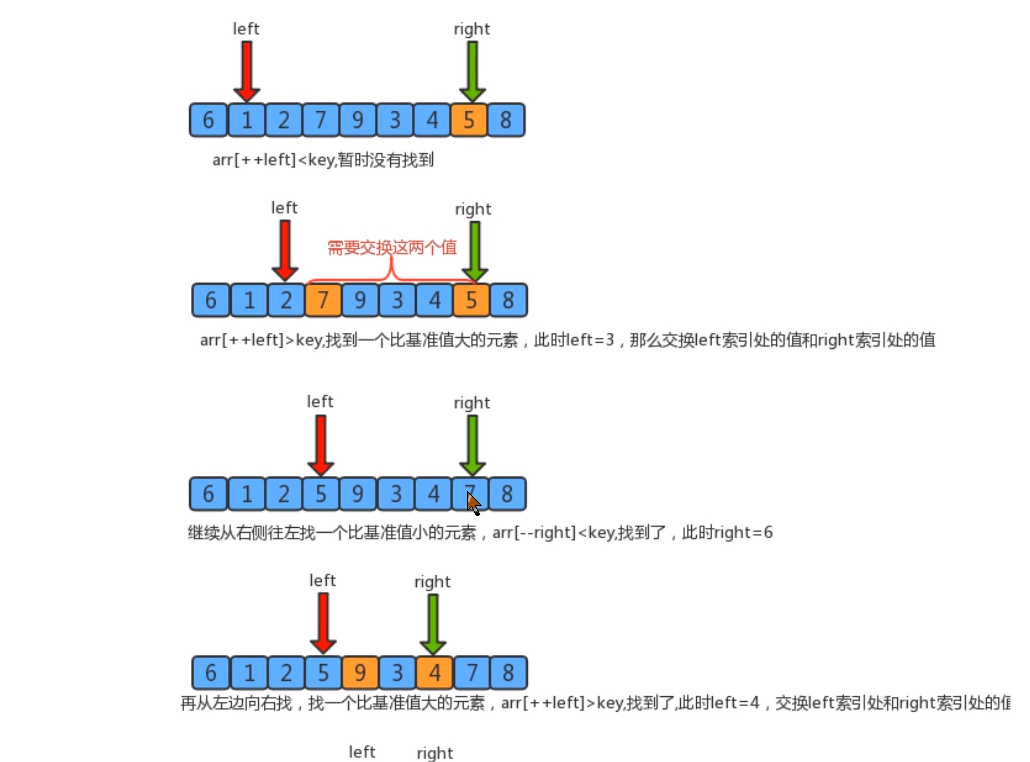
        while (true){
            //The right pointer moves to the left and stops when a value smaller than key is found
            while (less(a[key],a[--right])){
                if (right==lo){
                    break;
                }
            }

            //The left pointer moves to the right and stops when a value greater than key is found
            while (less(a[++left],a[key])){
                if (left==hi){
                    break;
                }

            }

            if (right<=left){
                break;
            }else{
                exch(a,right,left);
            }
        }

        //Exchange the element corresponding to the right pointer with the key (the right pointer points to the value less than the key)
        exch(a,lo,right);



        return right;

    }
}

package quick;

import java.util.Arrays;

public class QuickTest {
    public static void main(String[] args) {
        Integer[] a = {6,1,2,7,9,4,4,5,8};
        Quick1.sort(a);
        System.out.println(Arrays.toString(a));
    }
}

2.3 complexity analysis

• Difference between quick sort and merge sort:

  • Merge sort divides the array into two sub arrays, sorts them respectively, and merges the ordered group arrays to sort the whole array; The quick sort method is that when both arrays are in order, the whole array will be in order naturally
  • In merge sort, an array is divided into two parts, and the merge call occurs before processing the whole array. In quick sort, the position of the split array depends on the content of the array, and the recursive call occurs after processing the whole array. (one is to sort after segmentation, and the other is to sort before segmentation)

• Quick sort complexity analysis
  The first segmentation of quick sort starts from both ends until it coincides with right. Therefore, the time complexity of the first segmentation algorithm is O(n), but the time complexity of the whole quick sort is related to the number of segmentation.

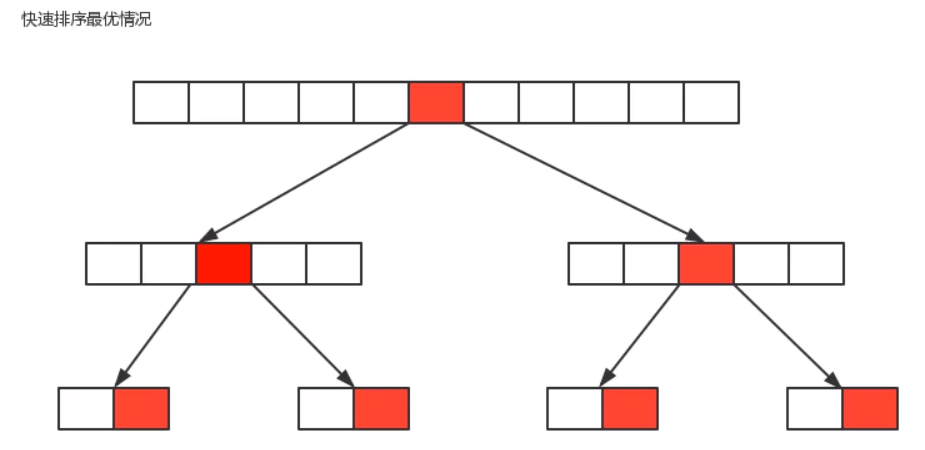
  • Best case:
    The reference number selected for each segmentation just divides the current sequence equally: O(nlogn)
    

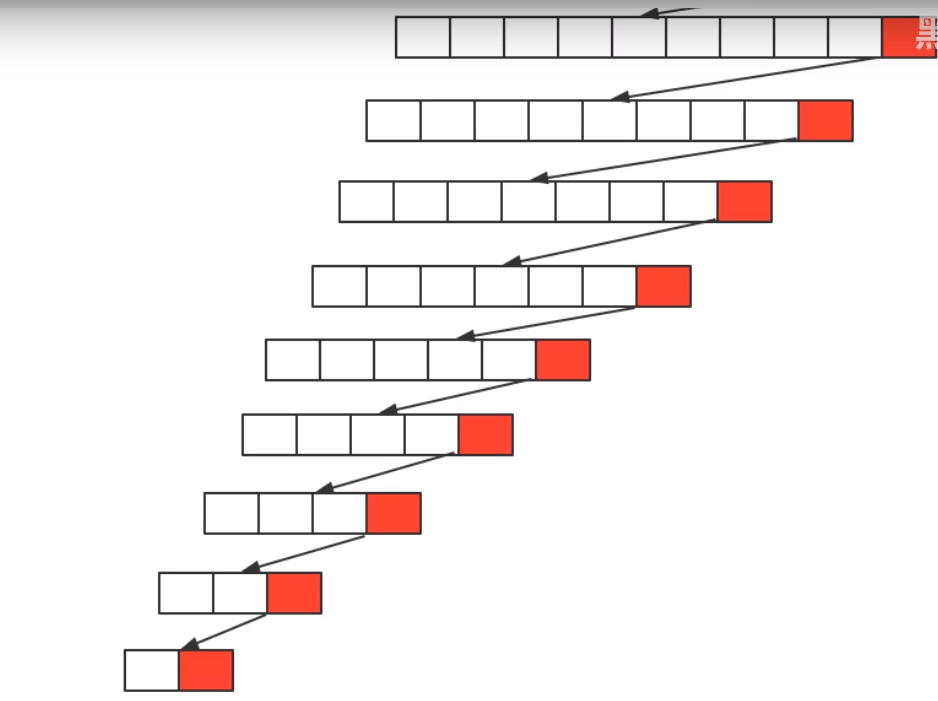
  • Worst case scenario:
    The benchmark number selected for each segmentation is the maximum number or the minimum number in the current sequence, which makes [each segmentation will have a subgroup], so it will be segmented n times in total. Therefore, in the worst case, the time complexity of quick sorting is O(n^2)

  

• Average: mathematical induction: O(nlogn)

Stability of sorting

• Stability of sorting:
  There are several elements in array arr, in which element A is equal to element B, and element A is in front of element B. If A sorting algorithm is used, it can be said that the algorithm is stable.

• Meaning of stability:
  Multiple sorting requires the selection of stable algorithms

• Ranking stability analysis
  If the core part of sorting encounters [large exchange], it will be unstable. That is, in the process of sorting, the data is not continuously inserted into the ordered array.

  • Bubble sorting stability: stable
  • Selective sorting: unstable, (directly select the minimum value, find the minimum value in the unordered array, and exchange the value at the minimum index)
    When {5 (1), 8,5 (2), 2,9} 5 (1) and 2 are compared, 2 is placed first, and 5 (1) is placed in the original position of 2, so 5 (1) and 5 (2) exchange positions
  • Insert sort: stable
  • Hill sorting: unstable: in the process of grouping, ordered arrays are not inserted continuously, with intervals
  • Merge sort: stable
  • Quick sort: unstable: when sorting, there is no continuous insertion of ordered arrays and exchange.