"This is the fourth day of my participation in 2022's first update challenge. See the activity details: 2022 first update challenge」

This blog post will be released in Nuggets community first!

subject

The daily practice is changed from the original > = 5 questions to > = 3 questions. There is no way, > = 5 questions are a little more.

First, let's have a simple one

Delete node in linked list

Input: head = [4,5,1,9], node = 5, output: [4,1,9] explanation: specify the second node with a value of 5 in the linked list. After calling your function, the linked list should be 4 - > 1 - > 9

There's nothing to say about this, hee hee~

class Solution {
    public void deleteNode(ListNode node) {
        node.val = node.next.val;
        node.next = node.next.next;
    }
}

Palindrome linked list

Give you the head node of a single linked list. Please judge whether the linked list is a palindrome linked list. If yes, return true; Otherwise, false is returned.

Normal solution

This is actually the same topic as we did before.
But now it is implemented in our linked list. Of course, the code is also simple.
The simplest and most direct idea is to get the value inside, and then give it to an array, and then judge.

class Solution {
    public boolean isPalindrome(ListNode head) {
        List<Integer> temp = new ArrayList<Integer>();

        // Copy the values of the linked list to the array
        ListNode currentNode = head;
        while (currentNode != null) {
            temp.add(currentNode.val);
            currentNode = currentNode.next;
        }

        // Use double pointer to judge whether palindrome
        int front = 0;
        int back = temp.size() - 1;
        while (front < back) {
            if (!temp.get(front).equals(temp.get(back))) {
                return false;
            }
            front++;
            back--;
        }
        return true;
    }
}

Of course, this is obviously not the best solution. In fact, we can still use this stack. The core of judging palindromes is to judge that the front is not equal to the back. If you use the stack, store it in order, and then compare it out of the stack one by one. In fact, it is equivalent to reversing the string. But this means scanning twice, the first time into the stack and the second time for comparison, but the previous method is double pointer, so it can be halved, and the second time is not so troublesome. But this method is too "simple" and does not meet our identity! So we need to use this stack. Yes, I've come to negative optimization again ~ we use recursion!

recursion

class Solution {
    private ListNode front;

    private boolean recursivelyCheck(ListNode currentNode) {
        if (currentNode != null) {
            if (!recursivelyCheck(currentNode.next)) {
                return false;
            }
            if (currentNode.val != front.val) {
                return false;
            }
            front = front.next;
        }
        return true;
    }

    public boolean isPalindrome(ListNode head) {
        
        front = head;
        return recursivelyCheck(head);
    }
}

Call me Dai Shi:

		Execution time:18 ms,Beat 5.45% of Java user
		Memory consumption:55.6 MB,Beat 7.19% of Java user

Median of data flow

The median is the number in the middle of a sequential table. If the list length is even, the median is the average of the middle two numbers.

For example,

The median of [2,3,4] is 3

The median of [2,3] is (2 + 3) / 2 = 2.5

Design a data structure that supports the following two operations:

• void addNum(int num) - adds an integer from the data stream to the data structure.
• double findMedian() - returns the median of all current elements.

The name is very whistling. In fact, it is very simple. The so-called median is that there is such a number, an array, half smaller than it and half larger than it. At the same time, pay attention to the parity of elements. Then we noticed that this is data flow, data flow! If you want to get the median, you must ensure that your sequence is orderly so that I can get the median at the complexity of O (1).

So the problem of this topic is how to ensure that the data input by users is in an orderly state!
If you add a data, I'll sort it once, using array Sort(), obviously, if this is done, if the amount of data is huge, it is a dead act. Moreover, we are a data stream, and the length of our data may change at any time, so we must be orderly when we let this data in.

So here we naturally think of large and small piles.

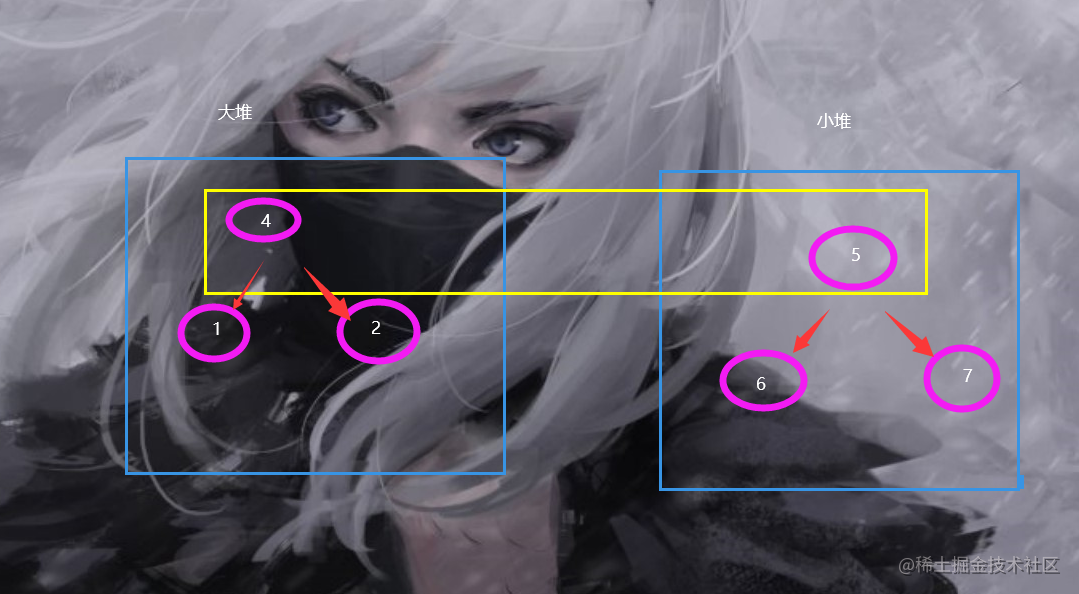
This is orderly. The problem is how to implement our code. At this time, we should reflect the benefits of our high-level language (to be honest, I can't write one by hand)

We use the PriorityQueue in java

PriorityQueue queue

This guy is based on a binary tree
(Note: the default PriorityQueue does not guarantee that the whole queue is orderly, but that the queue head is the smallest.)

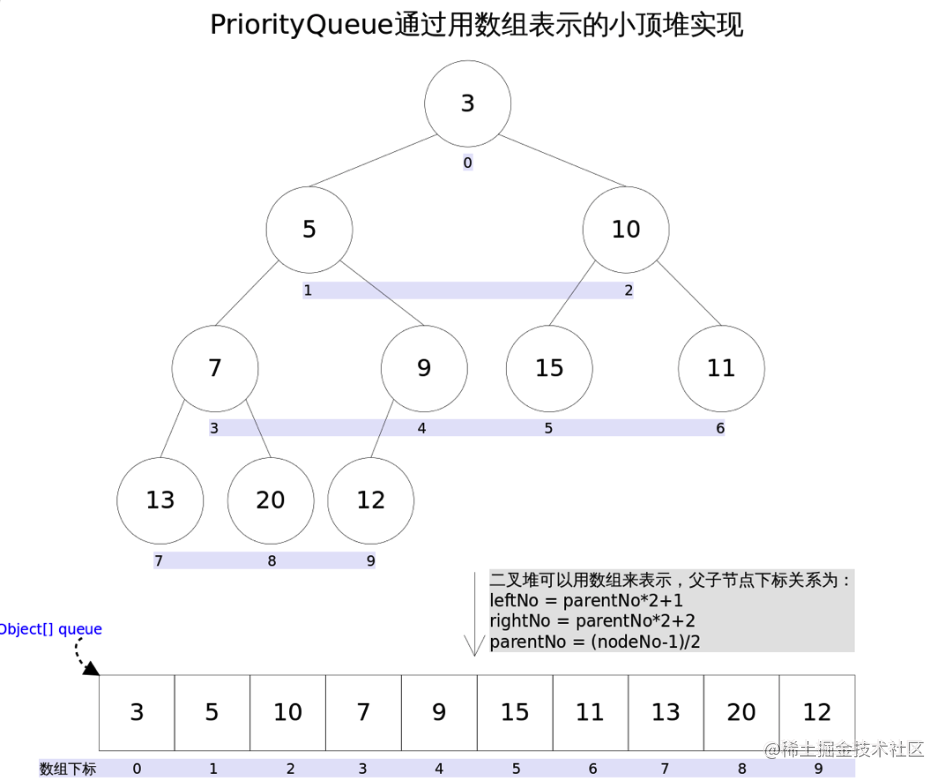
So if we want to implement a large root heap, we can do this.

PriorityQueue <Integer> A;
A=new PriorityQueue<>(new Comparator<Integer>() {

			@Override
			public int compare(Integer o1, Integer o2) {
				// if(o2>o1)
                                //      return 1;
                                // else
                                //     if(o1==o2)
                                //          return 0;
                                //     else
                                //         return -1;
				return o2-o1;
			}
});

Here, we use lambda directly

maxHeap = new PriorityQueue<>((a, b) -> b - a);

class MedianFinder {

    PriorityQueue<Integer> maxHeap;

    PriorityQueue<Integer> minHeap;
    public MedianFinder() {

        maxHeap = new PriorityQueue<>((a, b) -> b - a);
        minHeap = new PriorityQueue<>();
    }

    public void addNum(int num) {
        //First compare the two heap top elements to ensure that the large number is in the small heap and the small one is in the large heap
        if (maxHeap.size() == minHeap.size() + 1) {
            maxHeap.offer(num);
            minHeap.offer(maxHeap.poll());
           
        } else {
            minHeap.offer(num);
            maxHeap.offer(minHeap.poll());
        }
    }

    // When the number of elements in the data stream is odd, the median is the top element of maxHeap.
    // When the number of elements in the data stream is even, the median is the average number of top elements of maxHeap and minHeap.
    public double findMedian() {
        if (maxHeap.size() > minHeap.size()) {
            return maxHeap.peek();
        } else {
            return (maxHeap.peek() + minHeap.peek()) / 2.0;
        }
    }
}