70. Climb stairs
Simple difficulty
Suppose you are climbing stairs. You need n steps to reach the roof.
You can climb one or two steps at a time. How many different ways can you climb to the roof?
Note: given n is a positive integer.
Example 1:
Input: 2 Output: 2 Explanation: there are two ways to climb to the roof. 1. 1 rank + 1 rank 2. 2 rank
Example 2:
Input: 3 Output: 3 Explanation: there are three ways to climb to the roof. 1. 1 rank + 1 rank + 1 rank 2. 1 rank + 2 rank 3. 2 rank + 1 rank
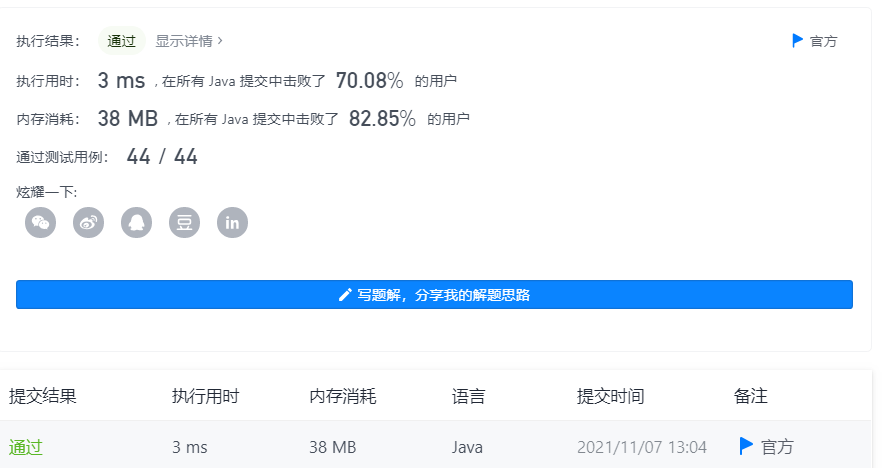
official
Idea: dynamic programming f(x)=f(x−1)+f(x−2) f(0)=1 f(1)=1 It feels like a Fibonacci sequence Scrolling arrays are used
class Solution {
public int climbStairs(int n) {
int p = 0, q = 0, r = 1;
for (int i = 1; i <= n; ++i) {
p = q;
q = r;
r = p + q;
}
return r;
}
}
198. House raiding
Medium difficulty
You are a professional thief who plans to steal houses along the street. There is a certain amount of cash hidden in each room. The only restrictive factor affecting your theft is that the adjacent houses are equipped with interconnected anti-theft systems. If two adjacent houses are intruded by thieves on the same night, the system will automatically alarm.
Given a non negative integer array representing the amount stored in each house, calculate the maximum amount you can steal overnight without touching the alarm device.
Example 1:
Input:[1,2,3,1]
Output: 4
Explanation: stealing house 1 (amount of money = 1) ,Then steal house 3 (amount of money = 3).
Maximum amount stolen = 1 + 3 = 4 .
Example 2:
Input:[2,7,9,3,1]
Output: 12
Explanation: stealing house 1 (amount of money = 2), Stealing house 3 (amount of money = 9),Then steal house 5 (amount of money = 1).
Maximum amount stolen = 2 + 9 + 1 = 12 .
Tips:
- 1 <= nums.length <= 100
- 0 <= nums[i] <= 400
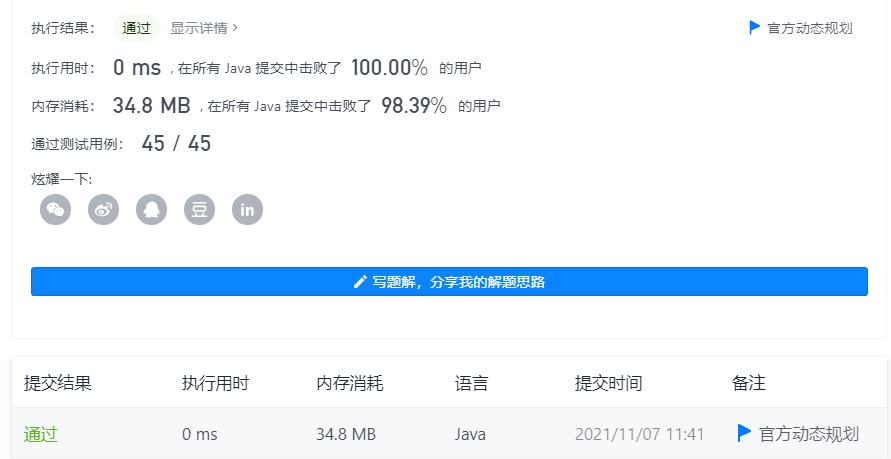
official
Idea: Simplest monadic problem Only one. I can only steal this one Only two, the one with a large amount of money k>2 Time Theft section k A house, then you can't steal it k−1 House, the total amount of theft is k−2 The maximum total amount of the second house is the same as that of the second house k The sum of the amount of each house. No stealing k House, the total amount of theft is k−1 The maximum total amount of a house. Select the option with a larger total amount of theft from the two options, and the total amount of theft corresponding to this option is the previous one k The maximum total amount that can be stolen from a house.
class Solution {
public int rob(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int length = nums.length;
if (length == 1) {
return nums[0];
}
int[] dp = new int[length];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for (int i = 2; i < length; i++) {
dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[length - 1];
}
}
The above method uses an array to store the results. Considering that the maximum total amount of each house is only related to the maximum total amount of the first two houses of the house, a rolling array can be used to store only the maximum total amount of the first two houses at each time.
class Solution {
public int rob(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int length = nums.length;
if (length == 1) {
return nums[0];
}
int first = nums[0], second = Math.max(nums[0], nums[1]);
for (int i = 2; i < length; i++) {
int temp = second;
second = Math.max(first + nums[i], second);
first = temp;
}
return second;
}
}
Complexity analysis
-
Time complexity: O(n)O(n), where nn is the length of the array. You only need to traverse the array once.
-
Spatial complexity: O(1)O(1). Using the rolling array, you can only store the maximum total amount of the first two houses without storing the results of the whole array. Therefore, the spatial complexity is O(1)O(1).
Author: leetcode solution
Link: https://leetcode-cn.com/problems/house-robber/solution/da-jia-jie-she-by-leetcode-solution/
Source: LeetCode
120. Triangle minimum path and
Medium difficulty
Given a triangle, find the minimum path sum from top to bottom.
Each step can only move to the adjacent nodes in the next row. Adjacent nodes here refer to two nodes whose subscript is the same as or equal to the subscript + 1 of the previous node. That is, if it is in the subscript i of the current row, the next step can be moved to the subscript i or i + 1 of the next row.
Example 1:
Input: triangle = [[2],[3,4],[6,5,7],[4,1,8,3]] Output: 11 Explanation: as shown in the following diagram: 2 3 4 6 5 7 4 1 8 3 The minimum path sum from top to bottom is 11 (i.e., 2) + 3 + 5 + 1 = 11).
Example 2:
Input: triangle = [[-10]] Output:-10
Tips:
- 1 <= triangle.length <= 200
- triangle[0].length == 1
- triangle[i].length == triangle[i - 1].length + 1
- -104 <= triangle[i][j] <= 104
Advanced:
Can you only use the extra space of O(n) (n is the total number of triangles) to solve this problem?
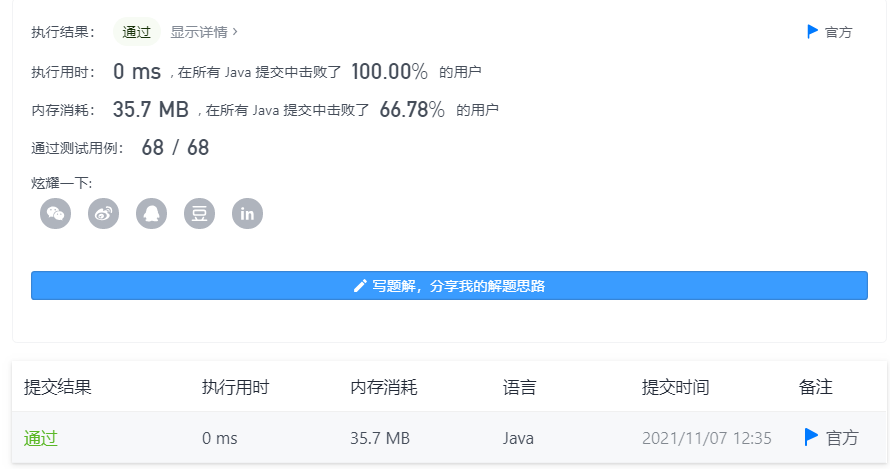
Problem solution
Idea: greedy algorithm I feel that greedy algorithm can be used Every time you go to the minimum, the total is the minimum
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int min=0;
int m=0;
int indexM=0;
for(int i=0;i<triangle.size();i++){
List<Integer> l=triangle.get(i);
if(i==0){
indexM=0;
m=l.get(0);
}else{
if(l.get(indexM)<l.get(indexM+1)){
m=l.get(indexM);
indexM=indexM;
}else{
m=l.get(indexM+1);
indexM=indexM+1;
}
}
min+=m;
}
return min;
}
}

Greed is not necessarily the smallest, but a relatively optimal solution
official
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int n = triangle.size();
int[][] f = new int[n][n];
f[0][0] = triangle.get(0).get(0);
for (int i = 1; i < n; ++i) {
f[i][0] = f[i - 1][0] + triangle.get(i).get(0);
for (int j = 1; j < i; ++j) {
f[i][j] = Math.min(f[i - 1][j - 1], f[i - 1][j]) + triangle.get(i).get(j);
}
f[i][i] = f[i - 1][i - 1] + triangle.get(i).get(i);
}
int minTotal = f[n - 1][0];
for (int i = 1; i < n; ++i) {
minTotal = Math.min(minTotal, f[n - 1][i]);
}
return minTotal;
}
}