876. Intermediate node of linked list

Title Description

Given a non empty single linked list with head node, return the intermediate node of the linked list.

If there are two intermediate nodes, the second intermediate node is returned.

Sample

Input:[1,2,3,4,5]
Output:[3,4,5]
Explanation: the returned node value is 3  (The serialization expression of this node in the evaluation system is [3,4,5]). 
We returned one ListNode Object of type ans，
So: ans.val = 3, ans.next.val = 4, 
ans.next.next.val = 5, ans.next.next.next = NULL.

Train of thought 1

Traversal twice, because the linked list cannot access an element in the linked list through subscript, and I don't know how many nodes there are in total. Therefore, we can count the number of nodes in the linked list through the first traversal; Second traversal: after traversing count/2 times, you can find the intermediate node and return.

Reference code

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        ListNode* h=head;
        int count=0;
        //First traverse the linked list and count how many nodes there are
        while(h)
        {
            h=h->next;
            count++;
        }
        //Calculate the number of times required to reach the intermediate node
        count/=2;
        //Traverse count times
        while(count)
        {
            head=head->next;
            count--;
        }
        //At this point, the head is the intermediate node
        return head;

    }
};

Train of thought II

Double pointer: to judge whether there is a ring in the linked list, the commonly used is the fast and slow pointer. The fast pointer takes two steps at a time and the slow pointer takes one step at a time. This method can also be used for the intermediate node to be found here. When the fast pointer reaches the end of the linked list, the slow pointer just reaches the intermediate node and directly returns the slow pointer.
PS: it's so ingenious. I really didn't expect that the double pointer could be used in this way at the beginning. It suddenly became clear.

Reference code

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        //Double pointer: the fast and slow pointer is generally used in the linked list
        //It all starts with the pointer
        ListNode* fast=head;
        ListNode* slow=head;
        //The fast pointer takes two steps at a time and the slow pointer takes one step at a time
        //When the fast pointer reaches the end, the slow pointer reaches the intermediate node
        while(fast!=NULL&&fast->next!=NULL)
        {
            fast=fast->next->next;
            slow=slow->next;
        }
        return slow;

    }
};

19. Delete the penultimate node of the linked list

Title Description

Give you a linked list, delete the penultimate node of the linked list, and return the head node of the linked list.

Sample

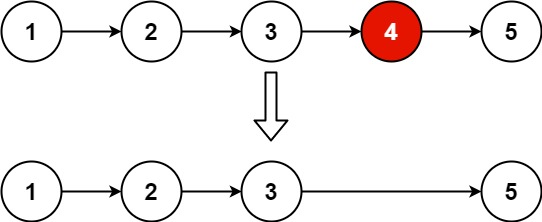
Input: head = [1,2,3,4,5], n = 2
 Output:[1,2,3,5]

Input: head = [1], n = 1
 Output:[]

Train of thought 1

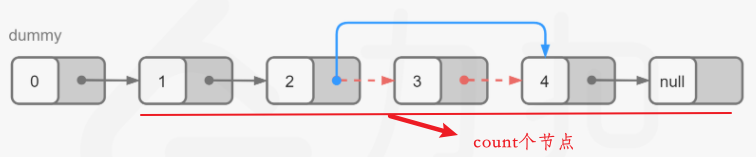
It is basically the same as the idea of the previous question. It is traversed twice. The first traversal counts the length of the linked list. The second traversal to the precursor node of the node to be deleted needs to traverse count-n times (including the dumb node) for deletion.
Note: for the linked list, to delete a node, you usually find the precursor node pre and point the next pointer of pre to the successor node of node. Therefore, if you want to delete the header node, you need to deal with it specially. The common method is to apply for a dumb node and point the pointer to the original header node. In this way, all nodes in the original linked list have precursor nodes and can be deleted normally.

Reference code

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* h=head;
        //First traversal: count the number of nodes in the original linked list
        int count=0;
        while(h)
        {
            count++;
            h=h->next;
        }
        //Second traversal: find the previous element of the node to be deleted
        //Dumb head node: to avoid deleting head nodes, special treatment is required
        ListNode* dummy=new ListNode(0,head);
        h=dummy;
        count=count-n;//Because there are many dumb nodes, it takes count-n times to arrive
        while(count)
        {
            h=h->next;
            count--;
        }
        //Delete operation
        h->next=h->next->next;
        return dummy->next;
    }
};

Train of thought II

Double pointer: you can still use the fast and slow pointer here. First, apply for dumb nodes to facilitate deletion. What we need here is to delete the penultimate node in the linked list, that is, we need to find the precursor node of the node to be deleted before we can delete it. You can first make the fast pointer advance n steps from the head node, and then make the fast and slow pointer advance one step at a time. When the fast pointer reaches the end, the slow pointer reaches the precursor node of the node to be deleted, * * the slow pointer starts from the dummy dummy node** After finding the precursor, delete it normally, and then return to the node

Reference code

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        //Double pointer again: fast and slow pointer
        //The fast pointer takes n steps first, and then walk together until the fast pointer is over, and the slow pointer will reach the answer.
        ListNode* dummy=new ListNode(0,head);
        //Initial value: the fast pointer is the original head, and the slow pointer is the dumb node
        ListNode* fast=head;
        ListNode* slow=dummy;
        //Go n steps first
        while(n--)
        {
            fast=fast->next;
        }
        //When the fast pointer reaches the end, the slow pointer reaches the precursor node of the penultimate node
        while(fast)
        {
            fast=fast->next;
            slow=slow->next;
        }
        //Delete operation
        slow->next=slow->next->next;
        return dummy->next;
    }
};