catalogue
two Arrays.stream sorting directly query adjacent duplicate
3. set storage (problem solving)
array
1 number of duplicates found
1. hashmap save times
Use map.get() to determine whether there is one. In fact, you can output it directly after determining whether there is one. You can use set instead of counting the number of times!
The feature of Set set is that it cannot store duplicate elements, cannot maintain the order of element insertion, and the key value can have at most one null value. The key in the Map has the same characteristics as the Set. Therefore, if the value value in the Map is regarded as a subsidiary of the key, all key values can form a value Set.
Since it is feasible to use the key of map here, it should be better to replace it with set!
public int findRepeatNumber(int[] nums) {
HashMap<Integer, Integer> map = new HashMap();
for (int i = 0; i < nums.length; i++) {
if (map.get(nums[i]) == null){
map.put(nums[i], 1);
}else {
return nums[i];
}
}
return -1;
}two Arrays.stream sorting directly query adjacent duplicate
public int findRepeatNumber_1(int[] nums) {
IntStream sorted = Arrays.stream(nums).sorted();
int[] sorted_array= sorted.toArray();
HashMap<Integer, Integer> map = new HashMap();
for (int i = 0; i < sorted_array.length - 1; i++) {
int temp = sorted_array[i];
if (temp == sorted_array[i+1])
return temp;
}
return -1;
}3. set storage (problem solving)
// Just save the value
public int findRepeatNumber_3(int[] nums) {
Set<Integer> set = new HashSet<Integer>();
int repeat = -1;
for (int num : nums) {
if (!set.add(num)) {
repeat = num;
break;
}
}
return repeat;
}Heterozygosity analysis
- Time complexity: O(n). Traverse the array once. Using HashSet, the time complexity of adding elements is O(1), so the total time complexity is O(n).
- Space complexity: O(n). Each element that is not repeated may be stored in the collection, so it takes O(n) additional space.

4. Use array index!
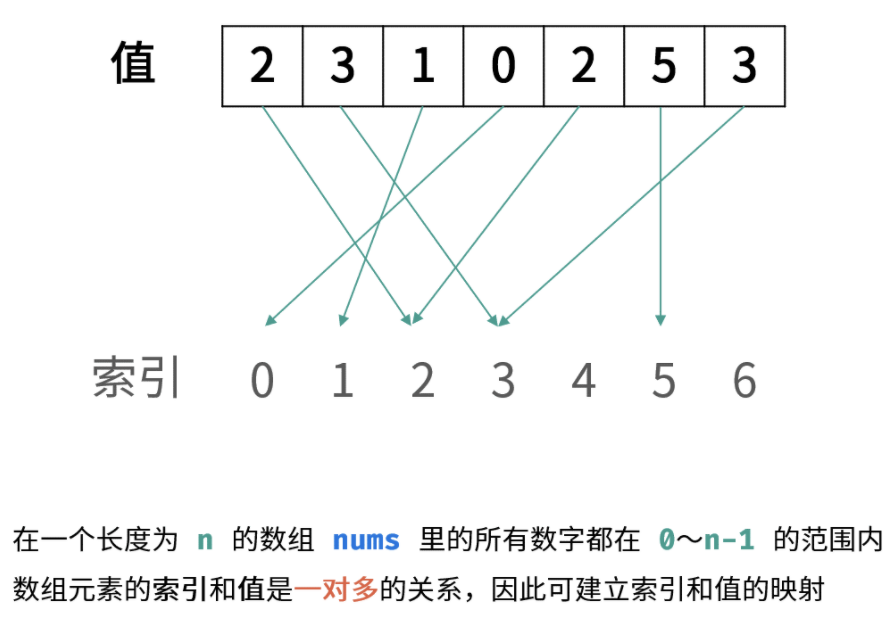
The title description has not been fully used, that is, all numbers in an array num of length n are in the range of 0 ~ n-1. The meaning of this description: the index and value of array elements are a one to many relationship.
- Scan the numbers in this array from beginning to end. When the number with subscript i is scanned,
- First, compare whether this number (represented by m) is equal to i
- If yes, then scan the next number;
- If not, compare it with the m-th number,
- If it is equal to the m-th number, a duplicate number is found (it appears at both subscripts i and m)
- If it is not equal to the m-th number, exchange the i-th number with the m-th number and put m in its position
- Then repeat the process of comparison and exchange until we find a duplicate number.
The key point is that I is incremented only when num [i] = = I, so as to ensure that the processing of some elements will not be missed before finding the same element.
//The mistake is that only when nums[i]==i + + I can all return to the original position
public int findRepeatNumber_4(int[] nums){
for (int i = 0; i < nums.length; i++) {
if(nums[i] == i) {
continue;
}
if(nums[nums[i]] == nums[i]) return nums[i];
reverse(nums, i, nums[i]);
}
return -1;
}
public void reverse(int[] nums, int i, int j){
int temp ;
temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
public int findRepeatNumber_5(int[] nums){
int i = 0;
while(i < nums.length) {
if(nums[i] == i) {
i++;
continue;
}
if(nums[nums[i]] == nums[i]) return nums[i];
int tmp = nums[i];
nums[i] = nums[tmp];
nums[tmp] = tmp;
}
return -1;
}
}
Complexity analysis:
- Time complexity O(N): O(N) is used to traverse the array, and O(1) is used for the judgment and exchange operation of each round of traversal.
- Spatial complexity O(1): additional space using constant complexity.
Continue to optimize the in-situ exchange problem solution~
public int findRepeatNumber_4(int[] nums){
for (int i = 0; i < nums.length ; i++) {
if ( nums[i] != i){
if (nums[nums[i]] == nums[i]){
return nums[i];
}else{
reverse(nums, i, nums[i]);
}
i--;
}
}
return -1;
}
public void reverse(int[] nums, int i, int j){
int temp ;
temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
public int findRepeatNumber_4_1(int[] nums){
for (int i = 0; i < nums.length ; i++) {
if ( nums[i] != i){
if (nums[nums[i]] == nums[i]){
return nums[i];
}else{
reverse(nums, i, nums[i]);
}
}
else{
i++;
}
}
return -1;
}
public void reverse(int[] nums, int i, int j){
int temp ;
temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
If the same code is executed many times, the memory consumption is biased~
If it's just time first, use a dictionary,
If you have space requirements, you can sort the array in place with a pointer,
If the interviewer requires that the original array cannot be modified, you can create an auxiliary array with a length of n+1. Copy each number of the original array to the auxiliary array one by one. If the original array copies m, copy it to the position where the subscript of the auxiliary array is m.
If the original array cannot be modified and the auxiliary space is also required to be O(1), the idea of dichotomy must be used,
Divide the number from 1 to n into two parts from the middle number m, the first half is 1~m, and the latter half is m+1~n. If the number of numbers from 1 to m exceeds m, then this half of the interval must contain repeated numbers; Otherwise, the interval of the other half m+1~n must contain repeated numbers. We can continue to divide the interval containing duplicate numbers into two until we find a duplicate number. This process is very similar to the binary search algorithm, except for one more step to count the number of numbers in the interval.
The number of numbers in the calculation interval should be called O(logn) times. Each call requires O(n) time. The total time complexity is O(nlogn) and the space complexity is O(1).
However, if a number appears many times, which is just equal to the total number of that interval, it can not be found.
For example, when {2,3,5,4,3,2,6,7} is encountered, there are two numbers in the range of {1,2} which is twice.
2. Sorted array lookup array
The first thought was hashmap
1. hashmap
// hashmap don't forget the situation that doesn't exist
// hashmap is suitable for sorting and non sorting
public int search(int[] nums, int target) {
HashMap<Integer, Integer> map = new HashMap();
for (int i = 0; i < nums.length; i++) {
if (map.get(nums[i]) == null){
map.put(nums[i], 1);
}else {
map.put(nums[i], map.get(nums[i])+1);
}
}
return map.get(target) != null ? map.get(target):0;
}Time complexity O(n)
Spatial complexity O(n)
2. Traversal
public int search_1(int[] nums, int target) {
int n = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] == target){
n++;
}
}
return n;
}Time complexity O(n)
Space complexity O(1)
2_ 1. Traversal optimization
public int search_1_1(int[] nums, int target) {
int n = 0;
int temp = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] != target && temp == 1){
break;
}
if (nums[i] == target){
n++;
temp = 1;
}
}
return n;
}Add a temp to identify whether the search has been completed, use space for time, and the time complexity is O(n)
3. Dichotomy
class Solution {
public int search(int[] nums, int target) {
int leftIdx = binarySearch(nums, target, true);
int rightIdx = binarySearch(nums, target, false) - 1;
if (leftIdx <= rightIdx && rightIdx < nums.length && nums[leftIdx] == target && nums[rightIdx] == target) {
return rightIdx - leftIdx + 1;
}
return 0;
}
public int binarySearch(int[] nums, int target, boolean lower) {
int left = 0, right = nums.length - 1, ans = nums.length;
while (left <= right) {
int mid = (left + right) / 2;
if (nums[mid] > target || (lower && nums[mid] >= target)) {
right = mid - 1;
ans = mid;
} else {
left = mid + 1;
}
}
return ans;
}
} The official explanation is not very clear ~ it's only clear from the boss's explanation that the second version has been modified.

public int search_3(int[] nums, int target) {
// 1. Num [M] < target in [m+1,j], so i = m + 1
// 2. Num [M] > target target in [i,m-1], so j = m - 1
// 3. nums[m] == target
// Right boundary in [m+1,j], i = m + 1
// The left boundary is j = m - 1 in [i,m-1]
// so find the right boundary nums [M] = = merge target into nums [M] < target is [m+1,j]
// That is, if (Num [M] < = target) I = m + 1;
// else j = m - 1;
// Find the left boundary num [M] = = merge target into num [M] > target is [i,m-1]
// That is, if (Num [M] < target) I = m + 1;
// else j = m - 1;
// Search right boundary
int i = 0, j = nums.length - 1;
int m = 0;
while(i <= j) {
m = (i + j) / 2;
if(nums[m] <= target) i = m + 1;
else j = m - 1;
}
// Exit the loop by j moving to the left, so i staying in place, and so is m
int right = i;
// If there is no target in the array, it will be returned in advance
if(j >= 0 && nums[j] != target) return 0;
// Search left border right
i = 0; j = nums.length - 1;
while(i <= j) {
m = (i + j) / 2;
if(nums[m] < target) i = m + 1;
else j = m - 1;
}
// Exit the loop by i moving right so j staying in place
int left = j;
return right - left - 1;
}Optimization based on: finding the right boundary After right = i, that is, Num [i] points to the right boundary, then nums[j] points to the rightmost target (if any)
Complexity analysis:
- Time complexity O(log N) : Dichotomy is logarithmic complexity.
- Spatial complexity O(1) : Several variables use additional space of constant size.
3 look for missing numbers
Sorting array search problem, first think of dichotomy to solve
Similar to the previous question, we use the dichotomy to find the left and right boundaries. This time, we only need to judge whether the conditions are equal.

class Solution {
public int missingNumber(int[] nums) {
int start = 0, end = nums.length - 1;
int mid = 0;
while(start <= end){
mid = ((end - start) >> 1) + start;
if(nums[mid] != mid)
end = mid - 1;
else
start = mid + 1 ;
}
return start;
}
}
 https://leetcode-cn.com/problems/zai-pai-xu-shu-zu-zhong-cha-zhao-shu-zi-lcof/
https://leetcode-cn.com/problems/zai-pai-xu-shu-zu-zhong-cha-zhao-shu-zi-lcof/