Title Source: LeetCode
LeetCode Month Emblem Title of the Day
1414. and the minimum number of Fibonacci numbers for K
Give you the number k, and return the smallest number of Fibonacci numbers for k, where each Fibonacci number can be used multiple times.
The Fibonacci number is defined as:
F1 = 1
F2 = 1
Fn = Fn-1 + Fn-2, where n > 2.
The data guarantees that a feasible solution can be found for a given k.
Example 1:
Input: k = 7
Output: 2
Interpretation: The Fibonacci numbers are: 1, 1, 2, 3, 5, 8, 13,...
For k = 7, we can get 2 + 5 = 7.
Example 2:
Input: k = 10
Output: 2
Interpretation: For k = 10, we can get 2 + 8 = 10.
Example 3:
Input: k = 19
Output: 3
Interpretation: For k = 19, we can get 1 + 5 + 13 = 19.
Tips:
1 <= k <= 10^9
class Solution {
public:
int findMinFibonacciNumbers(int k) {
if (k == 0) return 0;
if (k == 1) return 1;
// Find the largest fib no larger than k, and the result is in a
int a = 1, b = 1;
while (b <= k) {
b = a + b;
a = b - a;
}
return findMinFibonacciNumbers(k - a) + 1;
}
};
21. Merge two ordered chains
Merge two ascending list into a new ascending list and return. The new list is made up of all the nodes of a given two list of chains.
Example 1: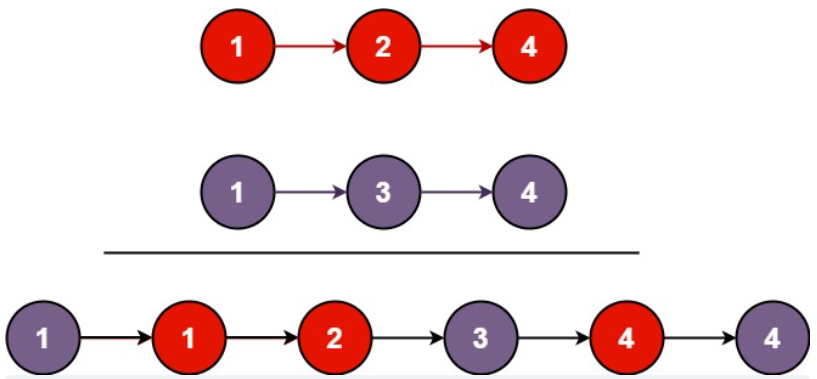
Input: l1 = [1,2,4], l2 = [1,3,4]
Output: [1,1,2,3,4,4]
Example 2:
Input: l1 = [], l2 = []
Output: []
Example 3:
Input: l1 = [], l2 = [0]
Output: [0]
Tips:
The range of the number of nodes in the two linked lists is [0, 50]
-100 <= Node.val <= 100
l1 and l2 are in non-decreasing order
Method: Recursive
We can recursively define merge operations in two chained lists as follows (ignoring boundary conditions, such as empty chained lists):
list1[0]+merge(list1[1:],list2) list1[0]<list2[0]
list2[0]+merge(list1,list2[1:]) otherwise
That is, one node with a smaller head value of the two chains is merged with the merge operation results of the remaining elements.
algorithm
We will directly model the above recursive process, taking into account the boundary conditions.
If l1 or l2 started out as empty chained lists, then there is no operation to merge, so we just need to return to the non-empty chained list. Otherwise, we want to determine which of the l1 and l2 chain table's header nodes has a smaller value, and then recursively decide which one to add to the result. If one of the two linked lists is empty, the recursion ends.
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
if (list1 == nullptr) {
return list2;
} else if (list2 == nullptr) {
return list1;
} else if (list1->val < list2->val) {
list1->next = mergeTwoLists(list1->next, list2);
return list1;
} else {
list2->next = mergeTwoLists(list1, list2->next);
return list2;
}
}
};
Complexity analysis
Time Complexity: Gives a recursive algorithm whose time complexity O(T) is usually the product of the number of recursive calls (counted as R) and the calculated time complexity (expressed as O(s)): O(T)=R_O(s). O(n + m), where N and m are the lengths of two chains, respectively. Because each call recursively removes the l1 or l2 header nodes (until at least one list is empty), the function mergeTwoList will only recursively call each node at most once. Therefore, the time complexity depends on the length of the merged list, O(n + m).
Spatial complexity: O(n + m), where N and m are the lengths of two linked lists, respectively. Recursive calls to the mergeTwoLists function consume stack space, which depends on the depth of the recursive call. The mergeTwoLists function calls n + m times at most when ending recursive calls, so the spatial complexity is O(n + m).
25. K sets of flip chains
Give you a list of links, one set of each k node is flipped. Please return to the flipped list.
k is a positive integer whose value is less than or equal to the length of the list.
If the total number of nodes is not an integer multiple of k, keep the last remaining nodes in their original order.
Advanced:
Can you design an algorithm that uses only constant extra space to solve this problem?
You can't simply change the value inside a node, you need to actually swap the nodes.
Example 1:
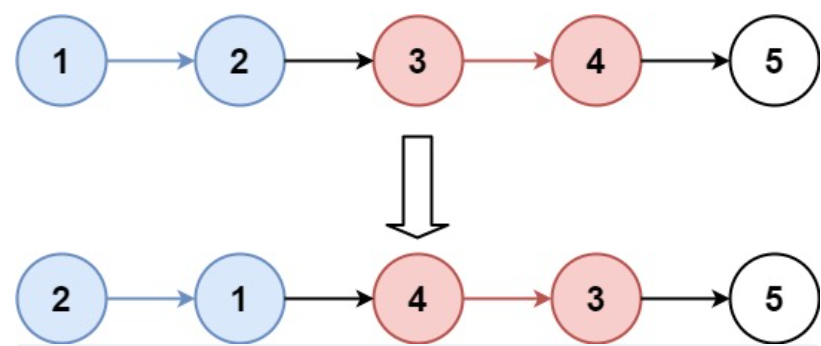Input: head = [1,2,3,4,5], k = 2
Output: [2,1,4,3,5]
Example 2:
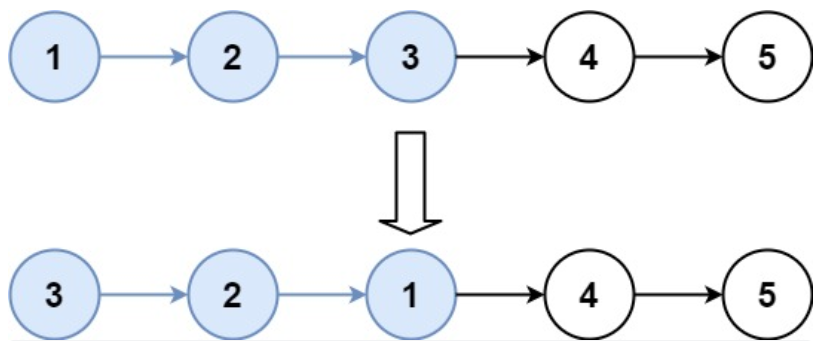
Input: head = [1,2,3,4,5], k = 3
Output: [3,2,1,4,5]
Example 3:
Input: head = [1,2,3,4,5], k = 1
Output: [1,2,3,4,5]
Example 4:
Input: head = [1], k = 1
Output: [1]
The approximate process can be broken down into
1. Find K nodes to be flipped (Note: if the remaining number is less than k, no flipping is required, so simply return to the head node of the part to be flipped).
2. Turn it over. And return to the flipped head node (note: flip to left closed and open interval, so the end of this round of operations is actually the head node of the next round of operations).
3. Flip the next k nodes.
4. Point the end of the previous turn to the head node after the next turn, that is, connect the k nodes of each turn.
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
//Left Closed Right Open Interval
ListNode* reverse(ListNode* head, ListNode* tail){
ListNode* pre = NULL;
ListNode* next = NULL;
while(head != tail){
next = head->next;
head->next = pre;
pre = head;
head = next;
}
return pre;
}
ListNode* reverseKGroup(ListNode* head, int k) {
if(head == NULL || head->next == NULL)
return head;
ListNode* tail = head;
for(int i = 0; i < k; i++){
//If the remaining quantity is less than k, no inversion is required
if(tail == NULL) return head;
tail = tail->next;
}
//Reverse the first k elements
ListNode* newHead = reverse(head, tail);
head->next = reverseKGroup(tail, k);
return newHead;
}
};
206. Inverse Chain List
Give you the head node of the single-chain list, invert the list, and return the inverted list.
Example 1:
Input: head = [1,2,3,4,5]
Output: [5,4,3,2,1]
Example 2:
Input: head = []
Output: []
Method 1: Iteration
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* prev = NULL;
ListNode* curr = head;
while(curr){
ListNode* next = curr->next;
curr->next = prev;
prev = curr;
curr = next;
}
return prev;
}
};
Complexity analysis
Time complexity: O(n), where n is the length of the chain table. The list needs to be traversed once.
Spatial complexity: O(1).
Method 2:
@Lao Tang
Why can recursion be used? Because three conditions of recursion are met:
1. The big problem is split into two sub-problems
2. Subproblems are solved the same way as big problems
3. There are minimal subproblems
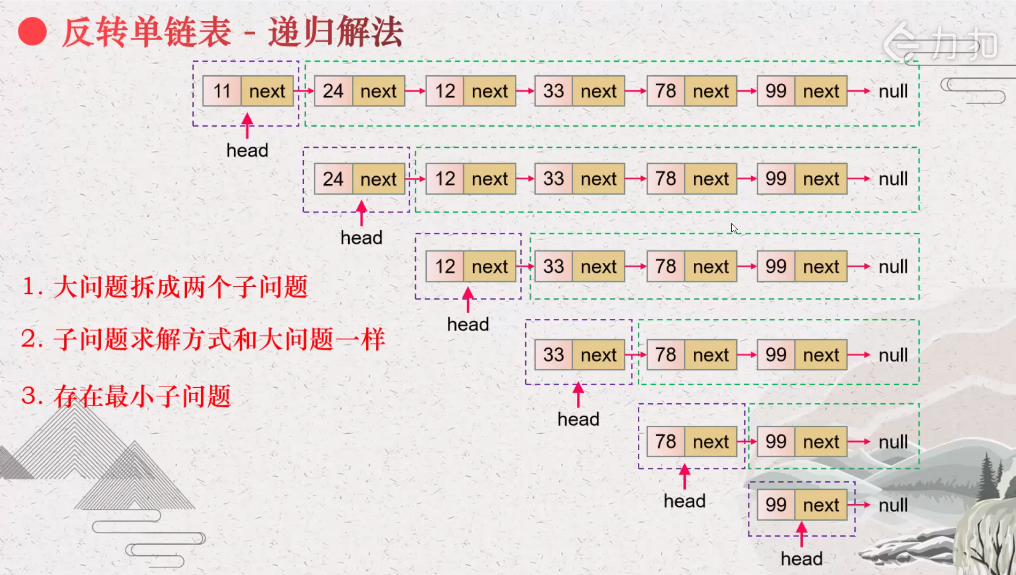
What happens before a recursive call is what happens when it is recursive, and what happens after a recursive call is what happens when it is recursive.
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(head == NULL || head->next == NULL) return head;
//Pass-through section above
ListNode* ans = reverseList(head->next);//Calling Recursive Functions
//Below is the Home Section
head->next->next = head;
head->next = NULL;
return ans;
}
};