1, Why use a tree as a data structure
1) Analysis of array storage mode
Advantages: it is fast to access elements by subscript. For ordered arrays, binary search can also be used to improve the retrieval speed.
Disadvantages: if a specific value is to be retrieved, or the inserted value (in a certain order) will move as a whole, which is inefficient [schematic]
2) Analysis of chain storage mode
Advantages: to a certain extent, the array storage mode is optimized (for example, if you insert a numerical node, you only need to link the inserted node to the linked list, and the deletion efficiency is also very good).
Disadvantages: when searching, the efficiency is still low, for example (to search a value, you need to traverse from the beginning of the node) [schematic diagram]
3) Analysis of tree storage mode
It can improve the efficiency of data storage and reading. For example, using binary sort tree can not only ensure the speed of data retrieval, but also ensure the speed of data insertion, deletion and modification.
[schematic diagram, detailed later]
Case: [7, 3, 10, 1, 5, 9, 12]
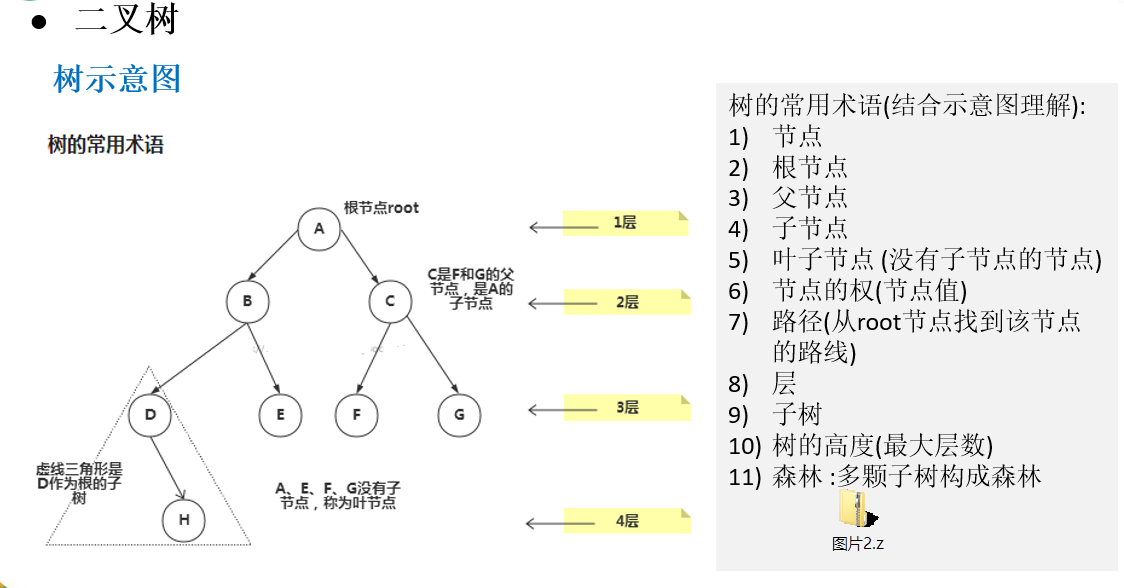
2, What is a binary tree
Binary tree diagram
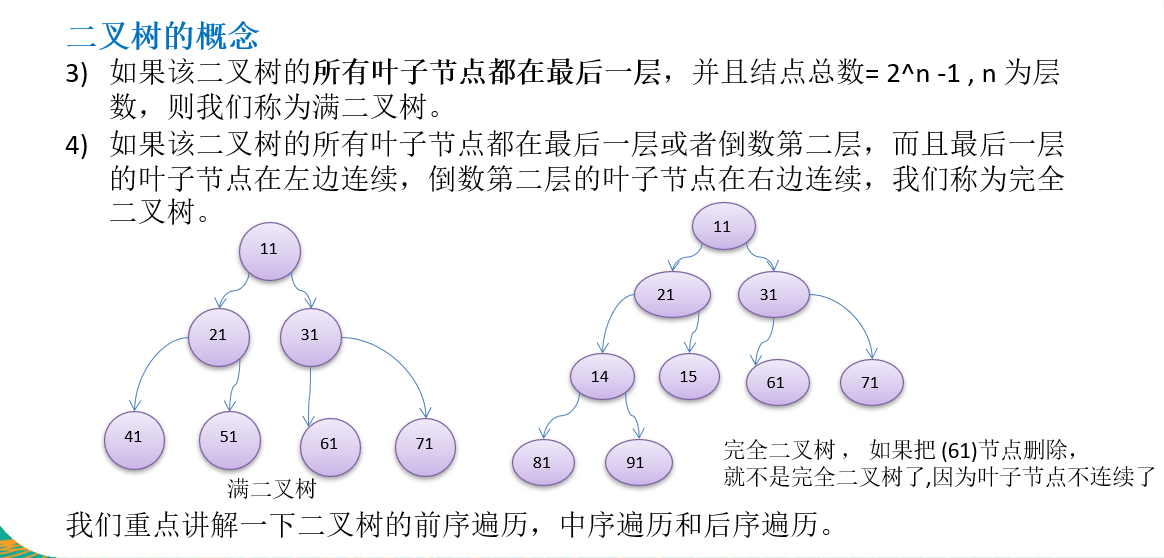
concept

3, Preorder traversal of binary tree
Traversal description
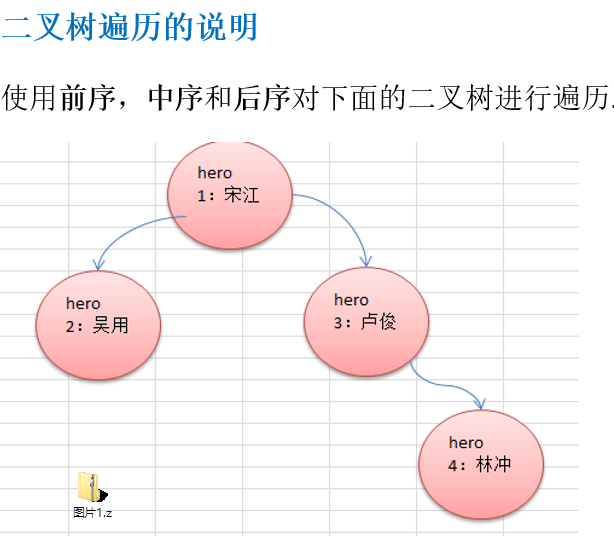
Preorder traversal: first output the parent node, and then traverse the left and right subtrees
Middle order traversal: first traverse the left subtree, then output the parent node, and then traverse the right subtree
Post order traversal: first traverse the left subtree, then traverse the right subtree, and finally output the parent node
Summary: see the order of output parent nodes to determine whether it is pre order, middle order or post order
Traversal requirements
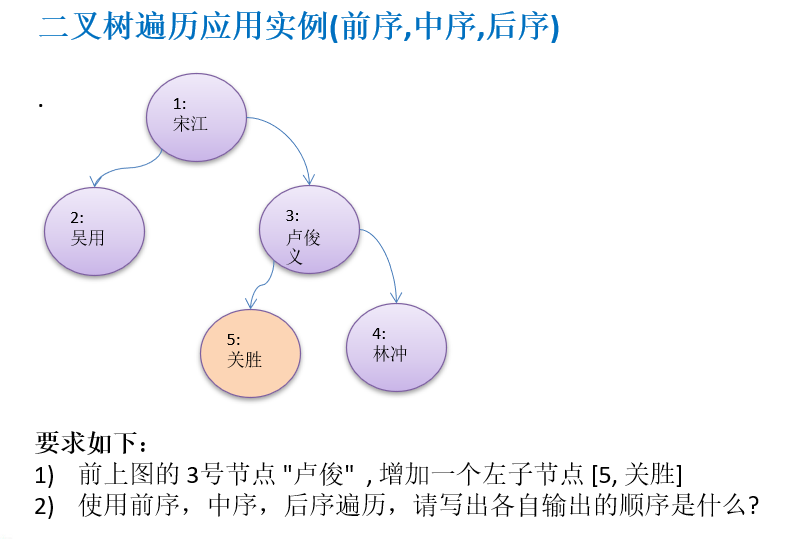
code implementation
package com.fafa.tree;
/**
* Binary tree
*
* @author Sire
* @version 1.0
* @date 2022-01-22 16:51
*/
public class BinaryTreeDemo {
public static void main(String[] args) {
// Create node
HeroNode root = new HeroNode(1, "Song Jiang");
HeroNode node2 = new HeroNode(2, "Wu Yong");
HeroNode node3 = new HeroNode(3, "Lu Junyi");
HeroNode node4 = new HeroNode(4, "Lin Chong");
HeroNode node5 = new HeroNode(5, "Wu Sheng");
// Manually generate the binary tree first (it will be generated by recursion later, and manually for the time being)
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
// Create binary tree
BinaryTree tree = new BinaryTree(root);
// Test preorder traversal
System.out.println("Preorder traversal");
tree.preOrder();
// Sequence traversal in test
System.out.println("Medium order traversal");
tree.infixOrder();
// Post test traversal
System.out.println("Postorder traversal");
tree.postOrder();
}
}
/**
* Create binary tree
*/
class BinaryTree {
HeroNode root = null;
public BinaryTree(HeroNode root) {
this.root = root;
}
/**
* Preorder traversal
*/
public void preOrder() {
if (this.root != null) {
this.root.preOrder();
} else {
System.out.println("This is an empty tree");
}
}
/**
* Medium order traversal
*/
public void infixOrder() {
if (this.root != null) {
this.root.infixOrder();
} else {
System.out.println("This is an empty tree");
}
}
/**
* Postorder traversal
*/
public void postOrder() {
if (this.root != null) {
this.root.postOrder();
} else {
System.out.println("This is an empty tree");
}
}
}
/**
* Hero node
*/
class HeroNode {
private int id;
private String name;
private HeroNode left;
private HeroNode right;
/**
* Construction method. The left and right nodes are empty by default
*
* @param id
* @param name
*/
public HeroNode(int id, String name) {
this.id = id;
this.name = name;
}
public int getId() {
return id;
}
public void setId(int id) {
this.id = id;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
/**
* Preorder traversal
* Idea:
* 1,Reprint parent node
* 2,Then judge whether the left subtree is empty. If not, print recursively
* 3,Judge whether the right subtree is empty. If not, print recursively
*/
public void preOrder() {
// Why can you print directly without judging the root node? Because the transmitted node must be a valid node, you don't need to judge (it has been judged in the previous call layer)
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
/**
* Medium order traversal
* Idea:
* 1,First judge whether the left subtree is empty. If not, print recursively
* 2,Reprint parent node
* 3,Judge whether the right subtree is empty. If not, print recursively
*/
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
/**
* Postorder traversal
* Idea:
* 1,First judge whether the left subtree is empty. If not, print recursively
* 2,Judge whether the right subtree is empty. If not, print recursively
* 3,Reprint parent node
*/
public void postOrder() {
if (this.left != null) {
this.left.postOrder();
}
if (this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
}
4, Binary tree pre middle post order search
demand

code implementation
Add to the HeroNode class
/**
* Preorder traversal search
*
* @param no number
* @return
*/
public HeroNode preOrderSearch(int no) {
System.out.println("get into preSearch~");
// Compare whether the current node is
if (this.getId() == no) {
return this;
}
// Result node
HeroNode resNode = null;
// Compare left child nodes
// And traversal
// 1. Judge whether the current self rating point is empty. If not, continue to traverse the search (recursion)
// 2. If the left child node finds the result, it returns directly
if (this.left != null) {
resNode = this.left.preOrderSearch(no);
}
// If it is not empty, it indicates that it is found in the left subtree
if (resNode != null) {
return resNode;
}
// The same as above, except that the resNode can be returned directly in the end, because whether it is found or not, it is a resNode
if (this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
/**
* Middle order traversal search
*
* @param no number
* @return
*/
public HeroNode infixOrderSearch(int no) {
// Result node
HeroNode resNode = null;
// Compare left child nodes
// And traversal
// 1. Judge whether the current self rating point is empty. If not, continue to traverse the search (recursion)
// 2. If the left child node finds the result, it returns directly
if (this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
// If it is not empty, it indicates that it is found in the left subtree
if (resNode != null) {
return resNode;
}
// It should be placed in front of the comparison statement, not just in the front (because it counts the comparison times)
System.out.println("get into infixSearch~");
// Compare whether the current node is
if (this.getId() == no) {
return this;
}
// The same as above, except that the resNode can be returned directly in the end, because whether it is found or not, it is a resNode
if (this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
/**
* Postorder traversal search
*
* @param no number
* @return
*/
public HeroNode postOrderSearch(int no) {
// Result node
HeroNode resNode = null;
// Compare left child nodes
// And traversal
// 1. Judge whether the current self rating point is empty. If not, continue to traverse the search (recursion)
// 2. If the left child node finds the result, it returns directly
if (this.left != null) {
resNode = this.left.postOrderSearch(no);
}
// If it is not empty, it indicates that it is found in the left subtree
if (resNode != null) {
return resNode;
}
// The same as above, except that the resNode can be returned directly in the end, because whether it is found or not, it is a resNode
if (this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if (resNode != null) {
return resNode;
}
// It should be placed in front of the comparison statement, not just in the front (because it counts the number of comparisons)
System.out.println("get into postSearch~");
// If the left and right subtrees are not found
if (this.getId() == no) {
return this;
}
return null;
}
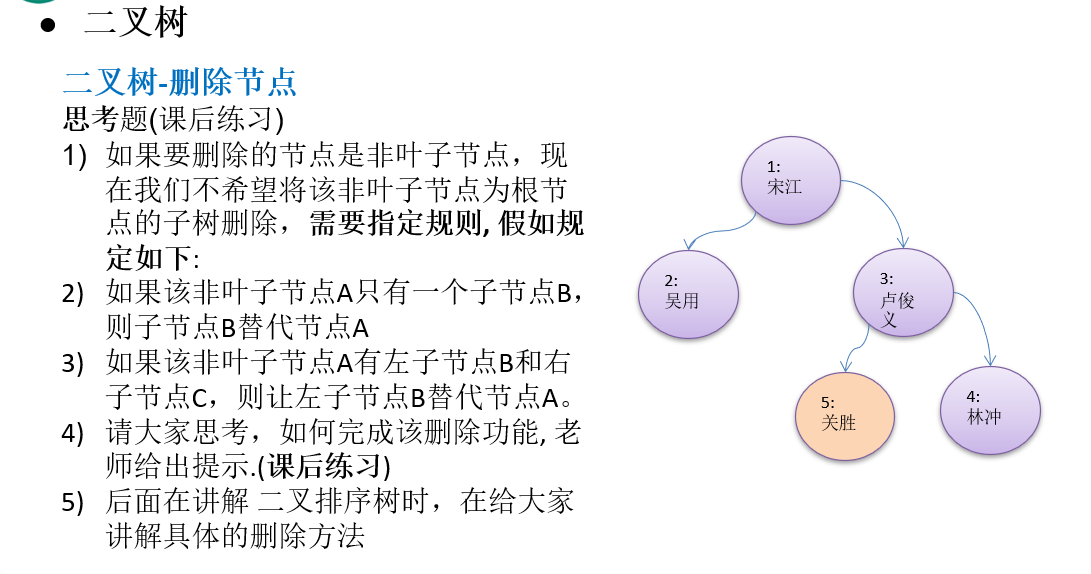
5, Delete node from binary tree
requirement

code implementation
Add in the HeroNode class
/**
* Recursively delete nodes
* 1,If the node to be deleted is a leaf node, you can delete the node directly
* 2,If the deleted node is a non leaf node, the subtree is deleted
*/
public void delNode(int no) {
//thinking
/*
* 1. Because our binary tree is unidirectional, we judge whether the child node of the current node needs to be deleted, but not whether the current node needs to be deleted
2. If the left child node of the current node is not empty and the left child node is to delete the node, set this left = null; And return (end recursive deletion)
3. If the right child node of the current node is not empty and the right child node is to delete the node, set this right= null ; And return (end recursive deletion)
4. If the node is not deleted in steps 2 and 3, we need to delete it recursively to the left subtree
5. If the node is not deleted in step 4, it should be deleted recursively to the right subtree
*/
if (this.left != null && this.left.getId() == no) {
// Leave blank
this.setLeft(null);
return;
}
if (this.right != null && this.right.getId() == no) {
this.setRight(null);
return;
}
if (this.left != null) {
this.left.delNode(no);
}
if (this.right != null) {
this.right.delNode(no);
}
}
Add in BinaryTree class
/**
* Delete node
* @param no
*/
public void delNode(int no) {
if (root != null) {
// This determines whether the node to be deleted is the root node
if (root.getId() == no) {
root = null;
} else {
root.delNode(no);
}
} else {
System.out.println("Empty number, unable to delete~");
}
}
After class thinking